The study of engineering lays more of a focus on mathematics and analytical thinking than other academic subjects. One of the outputs required for the accreditation of programs providing this education is to train engineers who have the ability to define, formulate/solve complex engineering problems, design under realistic constraints and conditions, and select/apply appropriate analysis/modeling methods for this purpose. In particular, fluid mechanics (a discipline that focuses on the study of fluids (liquids and gases) and the forces acting on them) and hydraulics (a subfield of hydrodynamics concerned with liquid flows in pipelines and open channels) courses, which are compulsory in the environmental and civil engineering curriculum, are considered to be the basic courses of scientific/technical education. These courses play a key role in providing the basic qualifications required to meet discipline-specific criteria in the accreditation of engineering undergraduate programs. In hydraulic engineering, the design of structures related to pressurized pipe flows and open channel flows (free surface flows) requires realistic and appropriate physical and mathematical modeling studies. In this regard, much faster and more precise results can be obtained compared to conventional methods by using effective programming languages in solving complex problems modeled with mathematical expressions. This study aimed to boost the incentive for computer-based technique in basic engineering education and to highlight its significance in solving four iterative open channel hydraulic problems. The MATLAB^® software was used to create computer-based solutions, and pertinent illustrations and coding information were provided in-depth for engineers, educators, and students. Moreover, student performances on midterm tests administered over the course of two consecutive semesters was evaluated in relation to manual problem solutions, and the challenges related to the traditional approach were examined within the scope of this study.

Keywords: combined sewer collector, compound channel, computer-aided approach, in-class assessment, Manning’s formula, MATLAB^® programming, open channel hydraulics

The real-world problems of fluid mechanics and hydraulics, which are among the most important research areas of environmental and civil engineering disciplines, are complex systems formed by the combination of many variables.¹ Especially in calculations at the project and design stage, one parameter is often a sub-function of the other, and when these sub-functions are combined to solve the targeted output, a sufficiently complex mathematical structure emerges for some problems.^2,3 In order to gain scientific background knowledge in engineering education, the solution of such complex equations is carried out conventionally, mostly by manual calculation. However, when the values of the variables of the problem are updated for different scenarios, the solution of the equations requires new iterations. This situation makes the applications quite time-consuming, laborious, and prone to error considering the human factor.⁴

Even the questions in the explicit form of some fluid mechanics and hydraulics problems,⁵ especially in the design and dimensioning types, bring a very long and intense workload, while the implicit forms make the solution challenging for engineers and students. At this point, computer-aided analysis facilitates the allocation of the problem into simpler modules in the numerical calculation environment and allows variables to be easily introduced into the solution algorithm for each new engineering scenario.^2,6 With properly coded algorithms to solve a particular problem, the value of the target variable is usually obtained within a few seconds, depending on the capacity of the computer system used and the complexity of the problem being solved. This saves time and cost in terms of evaluating many different scenarios in a short time.⁷

In the literature of computational flow analysis, numerous innovative and successful investigations have been conducted in the past few years. For instance, in a study conducted by Mohammadizadeh et al.,⁸ a network model was established to examine the flow transition in porous materials, and the impacts of diversity in certain hydraulic parameters were explored by this model. In addition, the network was evaluated using the combined pressurized-free surface network (CPFNET) approach. The authors reported that the CPFNET model results were found to be overall comparable to the experimental data. Another study highlighted the use of the submerged cavitation jet test method to evaluate cavitation erosion on solid surfaces.⁹ The cavitation jet apparatus (CJA) was described by the authors as essential for carrying out these experiments. Moreover, Gavidia et al.,¹⁰ employed an integrated artificial intelligence system (including SOM, Random Forest, XGBoost) to characterize mineralogy and facies in a carbonate reservoir located in the pre-salt region. They stated that conducting a thorough examination of different data sources helped to obtain important understandings about the reservoir’s features and enhance its efficiency. Furthermore, Moreover, Descovi et al.,¹¹ employed Long Short-Term Memory (LSTM) networks for the purpose of predicting river flow. The LSTM model utilized daily precipitation data to forecast stream flow in the area. The writers stated that LSTM’s main strength is its ability to recognize extended connections between precipitation and stream flow data, leading to precise forecasts of upcoming stream flow levels.

According to the author’s understanding, there is still a noticeable lack of transparent applications in the hydraulic field of education-focused computer programming. Only a few previous papers⁷ have presented complete MATLAB^®-based codes, provided a comparison of conventional and computer-based solution methods, and focused on in-class assessment for manual solution of fluid mechanics and hydraulics problems. The applications (both visually and numerically) and associated solution codes developed for the current analysis have not been used in any previous research on open channel hydraulics. In the present study, some original examples of open channel hydraulics (which are time-consuming and iterative in terms of manual calculations) and MATLAB^®-based scripts are presented along with the descriptions of the codes. The main goal of this research is to compare theoretical and computer-assisted methods (such as while 1/end loop and symbolic solution techniques) for engineers and students in related courses. Additionally, it aims to motivate them using computer technology to tackle additional problems that require iteration.

The structure of the present paper is organized in the following manner: The first section of “Materials and methods” begins with a brief overview of flow in open channels. The section “Representation of iterative open channel hydraulic problems” includes data and schematics of the four distinct iteration problems chosen for the current computational analysis. Information about the in-class assessment carried out as part of the manual solution approach, along with the criteria for evaluation, can be found in the section titled “Theoretical evaluation of manual solution of problems”. The applied computational solution methodology, diagrammatic calculation steps, and MATLAB^®-based scripts implemented in the solution of the selected open channel hydraulic problems examples are presented in the section “Computational procedure applied in solving iterative problems”. The section “MATLAB^®-based solutions of open channel hydraulic problems” contains details of fully executable codes, computational outputs from iterative or symbolic solutions of example problems, as well as results of additional simulations. The interpretations of the results and overall findings drawn from this work are outlined in the sections “Discussions” and “Conclusions” respectively.

A brief description of open channel flow

Within the domains of hydraulics and fluid mechanics, open channel flow refers to a kind of liquid movement in a conduit that has an exposed free surface to the atmosphere.¹² It covers the flow in creeks, rivers, natural or man-made (artificial) channels, water conveyance flumes, gutters, partially full pipes (sewers, drains), as well as the behavior of hydraulic structures such as weirs, spillways, and sluices.^13,14 Pipe flow is the other kind of flow that occurs inside a conduit. Although there are many similarities between these two types of flow, there is one key difference: pipe flow lacks a free surface, whereas open channel flow does, meaning that gravity rather than hydraulic pressure controls the flow.

The movement of fluid in a pipe that is not entirely filled is referred to as partially full pipe flow. In contrast to a fully developed pipe flow, in which the fluid occupies the entire pipe, a partially full pipe flow fills the channel only to a certain depth. A partially filled pipe can be thought of as having a flow that is similar to an open channel flow. This is due to the liquid inside the pipe having a free surface (liquid-gas interface), which is akin to open channels. In contrast to open channels, which have one side exposed to the atmosphere, closed conduit flows have an enclosed top width. The flow in a conduit is predominantly governed by gravity, just like in a river or canal, if it is not under pressure. The fluid’s velocity usually decreases close to the pipe’s surface and increases toward the free surface and the pipe’s core.

The concepts and formulae of open channel hydraulics, which make use of both the continuity equation and Manning’s equation,¹⁵ can be used to the analysis of partially filled pipe flows. The Manning’s formula (named after Irish hydraulic engineer Robert Manning who lived from 22 October 1816 to 09 December 1897), derived from the Chézy formula,¹⁶ (named after French physicist and hydraulics engineer Antoine de Chézy who lived from 01 September 1718 to 05 October 1798), is the most commonly used one for calculating uniform open channel flow calculations. Both of these equations are utilized in open channel and fluid dynamics investigations, and they are still widely taught. Because of its ease of use, shown effectiveness, and the fact that turbulent flow is the focus of the majority of open channel studies, the Manning’s formula is probably the one that is used the most frequently worldwide today for open channel uniform flow research.¹⁷

In the subject of fluid mechanics, Chézy’s semi-empirical formula is among the oldest, it covers a broader spectrum of flows than the Manning’s equation, and its influence is still felt today. It is a groundbreaking formula in the field of fluid mechanics that Manning refined and altered to create the Manning’s equation. The Chézy formula, which is well-known for its application in open channel flow computations, deals with the velocity of water flowing through conduits. Partially full pipe flow is likewise covered by the Chézy formula,¹⁸ according to the concept of open channel.

The formula is given by $V=C{R}_h^{1/2}{S}_0^{1/2}$ , where

V is the average velocity, C is the Chézy’s roughness coefficient,

R_h is the hydraulic radius (which is the cross-sectional area of flow divided by the wetted perimeter),

S₀ (or J) is the hydraulic gradient (which for uniform normal depth of flow is the slope of the channel bottom).

On 4 December 1889, at the age of 73, Manning first proposed his formula to the Institution of Civil Engineers (Ireland).

Manning derived an average empirical relation for Chézy’s roughness coefficient as $C=k\left[\left(1/n\right)R^{1/6}\right]$ , where

 k is a constant (k = 1 for SI units, and k = 1.486 for English units) and n is the Manning’s roughness coefficient. Hence, the final formula becomes $V=k\left[\left(1/n\right)R_h^{1/6}\right]R_h^{1/2}{S}_0^{1/2}$ , which gives the average velocity of flow as $V=\left(k/n\right)R_h^{2/3}{S}_0^{1/2}$ .

The following factors make Manning’s formula the most popular uniform flow equation in use worldwide:

(1) Manning’s approach is straightforward and supported by real-world examples,

 (2) A rough turbulent zone is where most open channel flows occur,

 (3) Since Manning’s n values are frequently determined from field measurements or tables, the Manning’s equation can be considered accurate. Surface roughness, channel alignment, imperfections in the cross-section, and vegetation all affect this coefficient.

In this section, a computational analysis is conducted on four different original iteration problems (side slope of a trapezoidal channel, expansion amount of a trapezoidal channel, depth of the cross section in a rectangular compound channel, and diameter of a circular combined sewer) under uniform flow conditions (constant slope and constant cross section) and MATLAB^®-based solutions are presented descriptions of the codes.

Problem 1: Determining the side slope (the horizontal distance for 1 m vertical distance) of a trapezoidal channel (Figure 1).

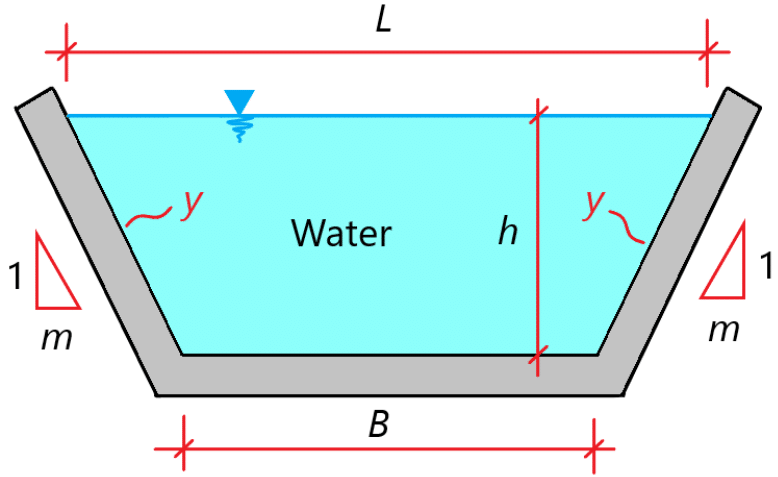
Figure 1 Schematic for Problem 1. The flow rate passing through the following trapezoidal channel is 2125080 L/hour. If the depth of uniform flow is 0.322 m, bottom slope of this channel is 1.322 m/km, Manning’s roughness coefficient is 0.01322, and bottom width (B) of the channel is 1.322 m, calculate the side slope (m) of this channel.

Problem 2: Determining the expansion amount of a trapezoidal channel (Figure 2).

Figure 2 Schematic for Problem 2. While the flow rate passing through the channel shown in the figure is Q, it is desired to double the flow rate passing through the channel without changing the depth. Calculate the amount of expansion (L) in the channel to meet the flow condition in question. The same material will be used for all surfaces of the channel and the bottom slope of the channel will remain constant.

Problem 3: Determining the depth in the cross-section of the rectangular compound channel (Figure 3).

Figure 3 Schematic for Problem 3. The flow rate of the man-made/regular riverbed or stream bed in the figure is 26550 L/s, and the bed slope for the whole channel is 0.001 m/m. If the Manning’s roughness coefficients for the meadow, flat ground, light shrub, and wooded parts forming the riverbed are 0.035, 0.030, 0.050, and 0.150, respectively, calculate the depth (h) in the cross-section of the rectangular compound channel with four segments of flow.

Problem 4: Determining the diameter of circular combined sewer collector (Figure 4).

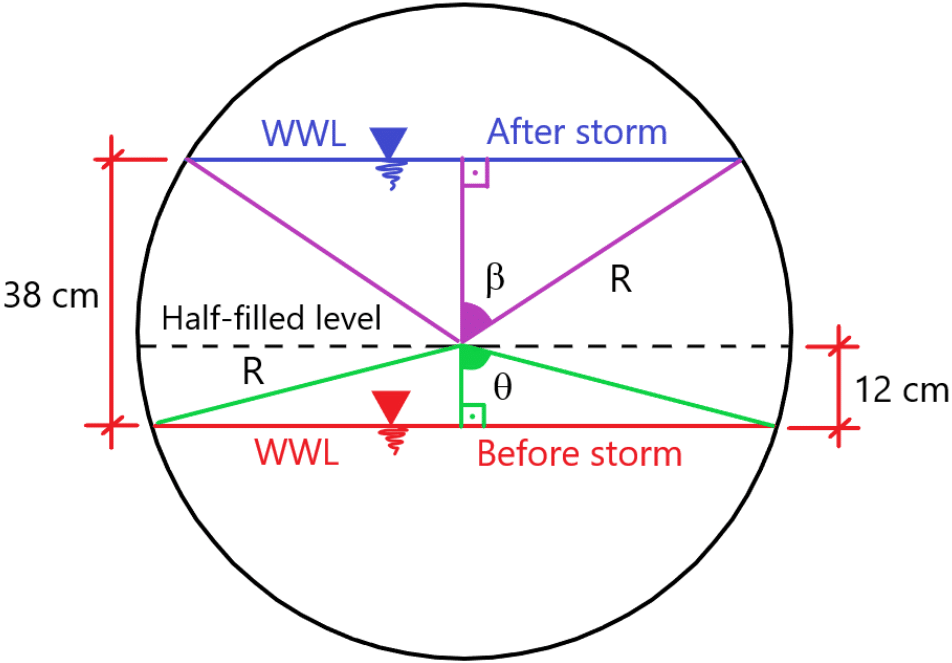
Figure 4 Schematic for Problem 4. The wastewaters originated from a residential region are transported to a wastewater treatment plant via a circular combined sewer (both wastewater and storm water flow through the same system) collector with a slope of 1.8 per thousand. In dry weather, the wastewater level (WWL) in the collector is 12 cm below the half-filled level. After a flooding event occurred in the area, the wastewater level has increased by 38 cm above the existing wastewater level. If the Manning’s roughness coefficient of the channel is 0.013 and the difference in flow rate before and after the flood 629.8 L/s, calculate the diameter of the channel.

In order to evaluate the computer-based approach in solving questions with an iterative character, student performances obtained from the manual method were also investigated within the scope of this study. For this purpose, two randomly selected questions (e.g., Problem 1 and Problem 3) from current open channel hydraulic problems were included in the midterms (belonging to the CEV2232 Hydraulics Mechanics for Engineers course) held in two consecutive semesters (2022-2023 spring semester and 2023-2024 spring semester). In these exams, it was seen that 39 and 87 undergraduate students (Department of Environmental Engineering, Faculty of Civil Engineering, Yildiz Technical University) were on the attendance lists, respectively, for the relevant semesters. Students were asked to solve each question in approximately 25-30 min using only their own handheld calculators (phone or internet use was prohibited by the instructor during the exam period). Because these were written exams (i.e., not multiple choice tests), students were scored according to their some meaningful mathematical effort (e.g., the extraction of some sub-formulas, iterations up to a certain stage, and so forth) while answering the questions. The “Discussion” section includes students’ manual solution performances regarding this in-class assessment.

In the present analysis, computer-based solutions are conducted by creating new solution scripts in the M-file Editor of MATLAB^® R2018a software (V9.4.0.813654, 64-bit (win64), Academic License Number: 40578168, MathWorks Inc., Natick, MA) running under Windows 10 PC platform (Casper Excalibur, Intel^® Core^TM i7-7700HQ CPU, 2.81 GHz, 16 GB of RAM, 64-bit). Figures 5–8 show pictorial illustrations for each hydraulic problem to provide a visual understanding of the implemented computational approach (Figures 5–8).

Figure 5 Diagrammatic representation of the steps involved in solving Problem 1.

Figure 6 Diagrammatic representation of the steps involved in solving Problem 2.

Figure 7 Diagrammatic representation of the steps involved in solving Problem 3.

Figure 8 Diagrammatic representation of the steps involved in solving Problem 4.

MATLAB^®-based solutions of open channel hydraulic problems

Tables 1–4 display the fully executable MATLAB^® codes for the four iterative-based open channel hydraulic problems. Figure 9–12 shows the computational outputs of the scripts evaluated in the “Editor Window”. It should be noted that the scripts offered here are enhanced with dialog and message boxes to give the user visible assistance in problem solving. Undoubtedly, readers can do pertinent computations on their own in MATLAB^®’s “Editor Window” or “Command Window” without utilizing data input/output windows (graphical user interface (GUI) interaction boxes) (Tables 1–4) (Figures 9–12).

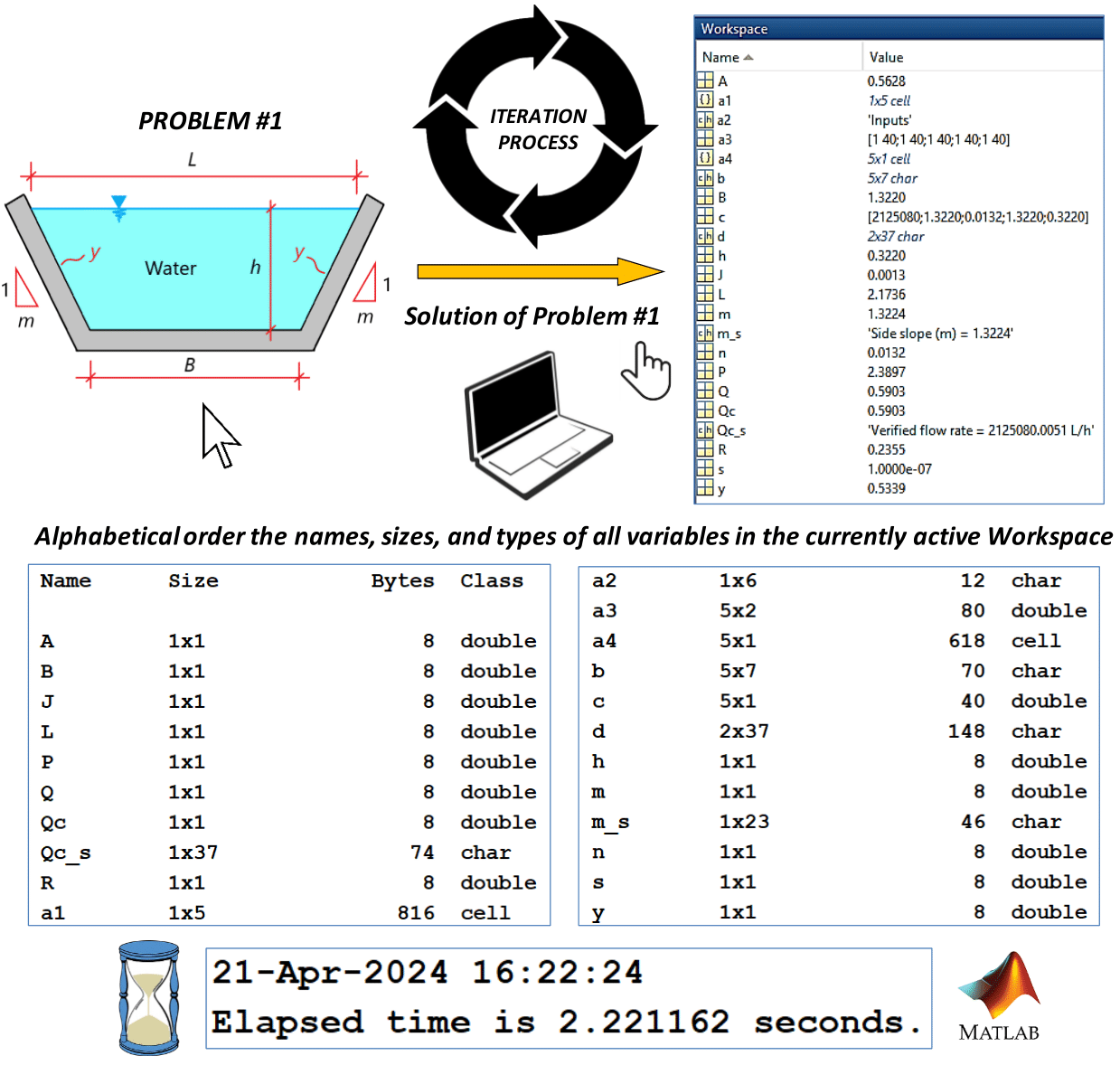
Figure 9 Contents of the “Workspace” window, sizes/types of variables, and elapsed times after running of the script (Table 1) for Problem 1.

Figure 10 Contents of the “Workspace” window, sizes/types of variables, and elapsed times after running of the script (Table 2) for Problem 2.

Figure 11 Contents of the “Workspace” window, sizes/types of variables, and elapsed times after running of the script (Table 3) for Problem 3.

Figure 12 Contents of the “Workspace” window, sizes/types of variables, and elapsed times after running of the script (Table 4) for Problem 4.

As flow rate is the main focus of all sample problems in this research, the values of the output variables resulting from changes in this key hydraulic parameter were determined for each case, and the results were analyzed mathematically. For this purpose, the input variables considered in each problem were kept constant for the values given in the relevant questions, but the flow rates were simulated within appropriate limits for the problems. Thus, the values of the targeted outputs were calculated within a total of 190 simulations related only to variations in flow rate parameter. For simulation studies, for/end and while 1/end loops were adapted to MATLAB^®-based scripts presented in Tables 1–4. For Problem 1 and 3, where the solution was achieved through an iteration process, only for/end loop was added to the relevant scripts. However, for Problem 2 and 4 where the solution was conducted symbolically, both for/end loop and while 1/end loop were added to the written code, and solution scenarios were implemented. It is noted that the modified codes used in simulation studies are not presented in this article due to page limitations, but can be provided upon request.

For Problem 1, flow rates passing through the trapezoidal channel (Q) values (Figure 5) ranging from 0.45 m³/s (1620000 L/h) to 1 m³/s (3600000 L/h) for 56 values (increment rate = 0.01 m³/s) have been calculated for side slope values (m). The calculated slope values ranged from 0.1682 to 6.1749. All simulations related to this problem were completed within 301.5731 seconds (5.0262 min). The best correlation between the calculated slope gradients and the considered flow values was achieved with a third-order equation. Using this equation, the side slope of 1.3361 was obtained for the sample flow rate (Q = 2125080 L/h = 0.5903 m³/s) in Problem 1. For this result and the value of 1.3224 m obtained from the script in Table 1, the absolute relative error (ARE) percentage (ARE (%) = abs((estimated value - true value) / true value) × 100) was calculated as 1.0340%. (Figure 13a).

For Problem 2, the expansion amount (L) in the trapezoidal channel was calculated for 60 values of flow rate increase (x) ranging from 1.05 to 4 (Figure 6) with an increment rate of 0.05 or 5%. The obtained expansion amounts ranged from 0.4492 m to 25.8544 m. All simulations for this problem were completed within 236.7496 seconds (3.9458 min). The best correlation between the calculated expansion amounts with the flow rates taken into account was achieved with a second-degree equation. By using this equation, the amount of expansion in the channel for the example flow rate increase value (x = 2 or 200%) in Problem 2 was obtained as 8.7663 m. ARE was determined as 0.1219% for this value and the value of 8.7770 m calculated from Table 2 (Figure 13b).

For Problem 3, flow rates (Q) in rectangular compound channels (Figure 7) have been calculated for 33 values ranging from 18 m³/s (18000 L/s) to 50 m³/s (50000 L/s) (increment rate = 1 m³/s) for the channel depth (h). The obtained section depths ranged from 1.0422 m to 3.2054 m. All simulations related to this problem were completed within 580.8903 seconds (9.6815 min). The best correlation between the calculated cross-sectional depths and the considered flow values was achieved with a third-order equation. Using this equation, the cross-sectional depth for the example flow rate (Q = 26550 L/s = 26.55 m³/s) in Problem 3 was obtained as 1.7225 m. ARE for this value and the calculated value of 1.7197 m from the script in Table 3 was found to be 0.1614% (Figure 13c).

For Problem 4, the flow rate difference (dQ) values in the circular combined sewer (Figure 8) have been calculated for 41 values ranging from 0.2 m³/s (200 L/s) to 1 m³/s (1000 L/s) (increase rate = 0.02 m³/s) for the channel diameter (D). The obtained channel diameters ranged from 0.5675 m to 1.3000 m. All simulations related to this problem were completed within 2182.1025 seconds (36.3684 min). The channel diameters calculated with the flow rate difference values taken into account are best provided with a second-order correlation equation. Using this equation, the channel diameter was obtained as 1.0004 m for the example flow rate difference value (dQ = 629.8 L/s = 0.6298 m³/s) in Problem 4. ARE of 0.0407% was calculated for this value compared to the value of 1.0000 m from Table 4 (Figure 13d).

Figure 13 Scatter plots and regression curves for changes in flow rate parameter and output variables for example open channel hydraulic problems (SEE stands for Standard Error of Estimate).

Simulation results have shown that there is a nonlinear relationship between changes in the flow parameter and target variables for fixed values of other inputs. Thanks to the applied programming technology, simulations in this study can also be performed for variations in other hydraulic and design parameters (e.g., channel bottom width, channel slope, Manning’s roughness coefficient, slope angle, etc.).

Engineering problems (particularly iterative-based problems) require a significant amount of energy and time to solve by traditional manual computations. Moreover, it becomes more challenging to obtain consistent results when there are more inputs or when basic mathematical calculation errors are made. For this reason, imparting computational approaches and modeling/simulation experiences to students is essential for equipping them with the necessary skills to address real-world challenges in their future careers. In this regard, powerful computer programs offer engineers a great deal of ease in making such calculations rather than trapping them in never-ending cycles and wasting time on the process of solving them.⁴

Scientists and software engineers use computation time as a key performance parameter to assess an algorithm’s ability to execute in an acceptable amount of time.¹⁹ The stopwatch timer code’s “Elapsed time is ... seconds” outputs (Figures 9–12) in the “Command Window” have shown that a significant amount of time and calculation needed to solve problems with implicit nature can be substantially decreased with the use of computational tools. For the purpose of observing the outcomes both numerically and visually, MATLAB^® offers a great educational environment.²⁰ These savings free up additional time for engineers and students to study and practice problems with various inputs. When it comes to execution speed, the MATLAB^®-based approach is always preferred in applications, even though the calculation times needed for combined channel and combined sewer problems are higher than other problems because of the size of the main equations to be solved. It is noted that students can explore various challenging aspects of current scenarios using the numerical and graphical tools in MATLAB^®, which offers powerful and flexible properties. Thanks to the program’s effective solution capability, various solution scenarios and applications can be created, allowing for a thorough analysis of the current issue from different viewpoints. For instance, if Problem 4 (circular combined sewer collector) is modified to include given values for channel diameter, slope, flow rate, and Manning’s roughness coefficient, with the task of finding the initial wastewater depth in the channel, then a conditional statement (e.g., if/else/end structure) needs to be incorporated into the solution algorithm. Utilizing the Manning’s equation straightforwardly as a calculator for flow in partially full pipes is challenging due to the complex equations involved in determining the area of flow and wetted perimeter for such conditions. In this scenario, the algorithm needs to determine if the flow in the channel is less than or greater than half-filled level and then analyze the angle of the wastewater surface as a function of the wastewater depth. Afterward, equations for wetted area and wetted perimeter need to be developed based on wastewater depth, and the appropriate solution should be derived using Manning’s formula. In this context, readers are encouraged to ponder the following question: “The wastewater from a residential area is carried to the wastewater treatment plant via a circular collector with a diameter of 0.90 meters and a slope of 4%. Determine the depth of wastewater in the channel when the flow rate is 850 L/s and the Manning roughness coefficient is 0.024”.

The midterm results for the spring semester of 2022-2023 revealed that only 18 of the 87 undergraduate students who took the test were able to complete Problem 3 (rectangular compound channel). The results from the spring semester of 2023-2024 showed that only 8 of the 39 undergraduate students who took the exam succeeded to solve Problem 1 (side slope of a trapezoidal channel) completely. For both semesters, the performance of fully solving the relevant questions was determined around 21%. While 64 of the 87 students who took the midterm exam in the spring semester of 2022-2023 could not obtain the full solution of the problem, they achieved a certain mathematical effort score. For this semester, 5 students did not try to solve the problem. Although 27 of the 39 students who took the exam in the spring semester of 2023-2024 were unable to determine the precise result, they attempted to solve the problem mathematically. The remaining 4 students did not take any action to solve the problem. Discussions were made with the students about the disadvantages of manual solutions to iteration-based questions. In particular, students stated that simple mathematical errors, choosing the correct starting values (initial guesses) for iterations, the length of the trial and error process, unit conversion, and difficulties in constructing and merging sub-functions are the primary factors that make solving such problems challenging.

Today, educators and engineering students benefit greatly from computer programs for digital-based applications like computing, design, analysis, modeling, and simulation. Incorporating contemporary, real-world, and efficacious methods that develop analytical and problem-solving abilities in students would be a huge plus for fluid mechanics and hydraulics courses. In this regard, computational thinking is a problem-solving method that entails breaking down intricate problems, identifying essential concepts, and improving solution strategies to boost problem-solving effectiveness.²² Additionally, encouraging students to solve complex problems through comprehension of programming logic without having them memorize codes would help them develop computational thinking abilities.²¹ The nature of mathematical thinking is highly connected to computational thinking as both involve an analytical problem-solving approach essential for programmers and computer scientists, due to the construction process required to solve mathematical problems.^23,24 For this aim, it should be noted that both students and engineers must have an effective mathematical background, as well as mastering the basic principles of fluid mechanics and hydraulics courses, and the logic of computer-based programming and algorithm creation.^7,24 Moreover, introducing a new curriculum that includes programming languages taught by specialized faculty will enhance students’ basic knowledge, technological skills, and confidence, benefitting their future professional endeavors.^7,25

In order to learn programming languages efficiently and permanently, applications should be repeated in computer environment at regular intervals, algorithms should be executed using different data, and the reader should make an effort to create their own algorithms after obtaining sufficient knowledge. More importantly, it is strongly recommended that the algorithms in question be written down verbatim both on paper and on the computer screen. Additionally, attempting to understand the significance of error or warning messages displayed on the screen will establish a crucial foundation for understanding how the program operates. In other words, it is obvious that algorithms cannot be efficiently learned just by reading or listening from someone without paper-pencil and screen-keyboard work.

In this study, four examples of open channel hydraulic problems, including two trapezoidal section channels, a rectangular compound channel used as a river bed, and a combined sewer collector, have been introduced with fully executable MATLAB^® codes for their loop- and symbolic-based solutions. Thanks to the solution methods presented in the present analysis, the calculation time has been significantly reduced and personal errors in manual solutions have been eliminated. Solution times of four iterative-based open channel hydraulic problems have been obtained as 2.2212, 0.2493, 13.0156, and 8.7553 seconds, respectively. When compared to the manual solution times (e.g., 25-30 min) of these problems, it has been seen that the proposed MATLAB^®-based approach can produce quantitative results with high precision in a very short time. The current analysis hopes to inspire engineers and students enrolled in this particular area of study to address other iteration-intensive issues by providing a comparison between conventional and computerized ways of thinking.

The author would like to thank Ms. Regina Cooper (Editorial & Review Analyst from MedCrave Group) who provided encouragement and time support during the creation of this work.

The author declares that he has no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

1. Pérez-Sánchez M, López-Jiménez PA. Continuous project-based learning in fluid mechanics and hydraulic engineering subjects for different degrees. Fluids. 2020;5(2):95.
2. Yetilmezsoy K, Bahramian M, Kıyan E, et al. Development of a new practical formula for pipe-sizing problems within the framework of a hybrid computational strategy. J Irrig Drain Eng. 2021;147(5):04021012.
3. Brkić D, Static Z, Živković M. Sizing pipes without iterative calculus: Solutions for head loss, flow discharge and diameter. In: 24th International Carpathian Control Conference (ICCC), Miskolc-Szilvásvárad. Hungary: 2023:71–76.
4. Almoulki T, Yetilmezsoy K. MATLAB for Iteration: Hydraulic modeling for environmental engineering students. Fluid Mech Res Int. 2019;3(1):24–28.
5. Babajimopoulos C, Terzidis G. Accurate explicit equations for the determination of pipe diameters. Int J Hydraul Eng. 2013;2(5):115–120.
6. Brkić D, Praks P, Praksová R, et al. Symbolic regression approaches for the direct calculation of pipe diameter. Axioms. 2023;12:850.
7. Yetilmezsoy K. IMECE—Implementation of mathematical, experimental, and computer‐based education: A special application of fluid mechanics for civil and environmental engineering students. Comput Appl Eng Educ. 2017;25(5):833–860.
8. Mohammadizadeh S, Moghaddam MA, Talebbeydokhti N. Analysis of flow in porous media using combined pressurized-free surface network. J Porous Media. 2021;24(10):1–15.
9. Mohammadizadeh S, Dalfré Filho JG, Descovi CS, et al. Assessing cavitation erosion on solid surfaces using a cavitation jet apparatus. Holos. 2023;5(39):e16306.
10. Gavidia JCR, Chinelatto GF, Basso M, et al. Utilizing integrated artificial intelligence for characterizing mineralogy and facies in a pre-salt carbonate reservoir, Santos Basin, Brazil, using cores, wireline logs, and multi-mineral petrophysical evaluation. Geoenergy Sci Eng. 2023;231:212303.
11. Descovi CS, Zuffo AC, Mohammadizadeh S, et al. Utilizing long short-term memory (LSTM) networks for river flow prediction in the Brazilian Pantanal Basin. Holos. 2023;5(39):e16315.
12. Chanson H. Hydraulics of open channel flow: An introduction, Basic principles, sediment motion, hydraulic modelling, design of hydraulic structures. Burlington, MA. Elsevier Butterworth-Heinemann. 2004.
13. Apsley D. Lecture Notes, Hydraulics 3, OCF Basics, Department of Mechanical, Aerospace and Civil Engineering. The University of Manchester; Manchester, U:. 2023.
14. Çengel YA, Cimbala JM. Fluid mechanics fundamentals and applications. New York: McGraw-Hill; 2014.
15. Gemici Z, Koca A, Kaya K. Predicting the numerical and experimental open-channel flow resistance of corrugated steep circular drainage pipes. J Pipeline Syst Eng Pract. 2017;8(3):04017004.
16. Zidan ARA. A review of friction formulae in open channel flow. Int Water Technol J. 2015;5(1):43–57.
17. Parsaie A, Najafian S, Yonesi H. Flow discharge estimation in compound open channel using theoretical approaches. Sustain Water Resour Manag. 2016;2:359–367.
18. Stefanyshyn DV, Khodnevich YV, Korbutiak VM. Estimating the Chézy roughness coefficient as a characteristic of hydraulic resistance to flow in river channels: a general overview, existing challenges, and ways of their overcoming. Environ Saf Nat Resour. 2021;39(3):16–43.
19. Harris-Birtill R, Harris-Birtill D. Understanding computation time: a critical discussion of time as a computational performance metric. In: Misztal A, Harris PA, Parker JA, editors. Time in Variance, Leiden. The Netherlands: Brill; 2021:220–248.
20. Yetilmezsoy K, Mungan CE. MATLAB time-based simulations of projectile motion, pendulum oscillation, and water discharge. Eur J Phys. 2018;39(6):1–18.
21. Arslan P. Teachers views’ and student qualifications for the basic programming course in vocational high schools. M.Sc. Thesis, Institute of Educational Sciences. Mersin University; Turkey: 2019.
22.  Saidin ND, Khalid F, Martin R, et al. Benefits and challenges of applying computational thinking in education. Int J Inf Educ Technol. 2021;11(5):248–254.
23. Barcelos TS, Muñoz-Soto R, Villarroel R, et al. Mathematics learning through computational thinking activities: a systematic literature review. J Univers Comput Sci. 2018;24(7):815–845.
24.  Isharyadi R, Juandi, D. A systematics literature review of computational thinking in mathematics education: Benefits and challenges. Formatif: Jurnal Ilmiah Pendidikan MIPA. 2023;13(1):69–80.
25. Magana AJ, Mathur JI. Motivation, awareness, and perceptions of computational science. Comput Sci Eng. 2012;14:74–79.