
Research Article Volume 1 Issue 1
Unambiguous determination of the wave impedance of slow-wave structures
Yuriy N Pchelnikov
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Pchelnikov’s Consulting, USA
Correspondence: Yuriy N Pchelnikov, Professor at Pchelnikov’s Consulting, USA
Received: April 18, 2017 | Published: June 19, 2017
Citation: Pchelnikov YN. Unambiguous determination of the wave impedance of slow-wave structures. Electric Electron Tech Open Acc J. 2017;1(1):1-5. DOI: 10.15406/eetoaj.2017.01.00001
Download PDF
Abstract
A new method of calculating the wave impedance of slow-wave structures (SWSs) based on the choice of an equivalent transmission line with decreased series inductance and increased shunt capacitance is demonstrated. It is shown that the calculation of the real conduction current in the longitudinal direction and the power flow makes it possible to find the equivalent voltage, which can be used for correcting parameters of the equivalent line. The proposed method is demonstrated using the example of a helix in the sheath approximation. Expressions for the equivalent inductance, capacitance, and voltage, which enable one to obtain the identical values of the wave impedance from all formulas of the circuit theory, are derived. Calculation of the power flow in SWS by differentiation of the “hot” dispersion equation is also considered.
Keywords: circuit theory, equivalent line, sheath helix, power flow, wave impedance
Abbreviations
SWSs: Slow-wave structure
Introduction
Microwave transmission lines, including waveguides and slow-wave structures (SWSs), are often replaced in their analysis and calculation by a two-wire equivalent circuit with series-parallel connection of inductors and capacitors and also resistors if the losses must be taken into account. In the cases of circuits homogeneous in the direction of the wave propagation, the equivalent circuit can be replaced by an equivalent line characterized by specific (per unit length) parameters. Practically all authors of monographs and textbooks on microwave engineering replace electrodynamics structures by equivalent circuits or equivalent lines in order to either simplify the analysis or simplify the physical interpretation of the obtained results.1–5 Such replacement substantially simplifies the calculation and matching of circuits with different geometries and different properties of filling materials. Unfortunately, in the case of electrodynamics structures, such as waveguides and slow-wave structures, traditionally defined equivalent parameters cannot be used for determination of the wave impedance Z0. It was well known, previously, that replacement of such transmission lines as cavity waveguides and SWSs, is not adequate and the wave impedance Z0 cannot be determined equally by all formulas of the circuit theory. For a long time, such the ambiguity was considered as an inevitable fact. In the fundamental textbook on microwave technique2 are demonstrated four expressions for the wave impedance of a rectangular waveguide, excited at H10 wave. The difference between these expressions is as large as twofold. Three significantly different formulas for the wave impedance of the mostly often used SWS, the helix, had been derived in monograph.6 All attempts of unambiguous determination Z0 for dispersive transmission lines were finishing by introducing a so-called "distribution coefficient"4 or transverse and longitudinal impedances.1,7
Unfortunately, the wave impedance is often confused with the introduced by Pierce interaction impedance,1 characterizing effectiveness of the slow wave interaction with the electron beam in vacuum devices. Being connected by the Maxwell's equations, both parameters differ not only by their physical meanings but also by their values.8 The parameter, determined as √L0/C0
, where L0 and C0 are specific (per unit length) equivalent inductance and equivalent capacitance, was called by Pierce “the transverse impedance” and was used just for an approximate estimation of the interaction effect. Despite of it, some authors use this parameter as the interaction impedance9 or as a parameter, which can be converted in the interaction impedance.10 Slow-wave structures are used mostly in delay lines and microwave vacuum devices.1,11 Other, so called “unconventional application of SWSs”,12 is just a developing brunch of the microwave engineering, being hindered by a narrow circle of specialists related to this specific area. The most developed among the unconventional applications are SWS-based electrodes for medical application,13 and sensors.14,15 Although the slowed electromagnetic wave can propagate without radiation along one, so called impedance electrode, as a rule, slow-wave structures are formed two electrodes, the second, a screen electrode, has a simple configuration, shielding the electromagnetic field. In the most traditional and unconventional applications, the gap between SWS electrodes is large enough to provide an effective coupling with the objects, such as an electron beam, treated material or human tissue, etc. In these cases, the longitudinal capacitive currents exceed, as a rule, the conduction current in the screen electrode and the wave impedance Z0 cannot be determined by the ratio U/I or √L0/C0
, where U and I are amplitudes of the potential on the impedance electrode and the conduction current in this electrode. The unambiguous determination of Z0 for slow-wave structures is represented below.
Initial definitions
Although slowing down of an electromagnetic wave can be provided by a homogeneous dielectric plate or a dielectric layer on a metal surface, the best results can be achieved by an impedance electrode, formed by a periodic row of conductors, connected in the longitudinal direction.12 The impedance electrode can be a meander line, a helix, or the other structure that increases the distance travelled by an electromagnetic wave. Let us consider an axially symmetric wave in a SWS formed by a cylindrical impedance electrode with average radius a, in a metal cylinder (screen electrode) with internal radius b (Figure 1). The origin of the cylindrical coordinate system r, ϕ, z is positioned on the axis of the helix. We will neglect by electromagnetic losses in the electrodes and in the surrounding medium.
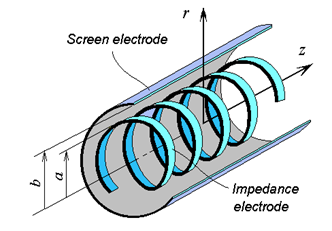
Figure 1 Helix (impedance electrode) in a metal cylinder (screen electrode).
All components of a slow wave will be taken to be proportional to the wave factor exp.(jωt-jβz), where t is time, ω is the angular frequency, and β is the phase constant along coordinate z (β = ω/vph, where vph is the phase velocity of the wave). Any SWS can be characterized by the slowdown N, defined as the ratio of the velocity of light c to the phase velocity of the wave in the SWS, or, that is the same, as
N=β/k, (1)
Where k is the wave number,
k=ω√ε0μ0
, (2)
ω is the angular frequency, and ε0, µ0 are the permittivity and permeability of free space.
The impedance electrode is assumed to be a periodic structure in z direction, with period T. When T is small compared with the wavelength (βT<<1), the impedance electrode can be replaced by an anisotropic surface with conductivity in the direction of the winds. This so called impedance approximation significantly simplifies analysis and allows using the equivalent line method. Unlike in waveguides, the phase constant β in slow wave structures always exceeds the wave number; in other words, N>1. In the simplest cases, when the wave front is perpendicular to the wave propagation direction, the electromagnetic field in the transverse cross section is symmetric and depends only on the transverse coordinate, e.g. radius r in axially symmetric structures. The transverse constant γ characterizing this dependence is related to the phase constant and the wave number as
γ2=β2−k2. (3)
Unlike the E- and H-waves in waveguides, which exist independently and may be characterized by different equivalent lines,16 slow waves in most SWSs are hybrid waves with components of both E- and H-waves. Having the same phase and group velocities, these waves satisfy different boundary conditions and their transverse distribution can be quite different.
Potential delay
In the impedance approximation, any SWS may be replaced by a two-wire transmission line (Figure 2) with series inductance per unit length L0 and shunt capacitance per unit length C0, in terms of which the phase constant is given by
β2=ω2L0C0
. (4)
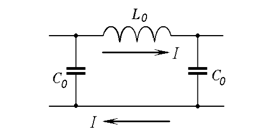
Figure 2 Two-wire equivalent line.
It follows from the rigorous electro-dynamic analysis,17 in the case of slow waves, the dominant part of L0, which we'll designate as L, is defined by the specific inductance of the impedance electrode, while a relatively small part, LD, is defined by the potential delay
L0=L+LD
. (5)
We emphasize that L depends on the magnetic flow excited by transverse currents, while LD depends on magnetic flow excited by longitudinal currents. In the case of a hybrid wave, L is defined by the H-wave, whereas LD is defined by the E-wave.
Substituting (5) in (4) and comparing with (3), we can identify
ω2LDC0≡k2
(6)
and
γ2=ω2LC0
. (7)
The replacement of L0 by L and traditional long line equation (4) by (7) makes it possible to use circuit theory for all SWSs.
Three-wire equivalent line
Unlike waveguides, which have only one area with a propagating wave, most SWSs have at least two areas adjacent to opposite surfaces of the impedance electrode. In some cases, for example when one area is filled by a dielectric material or electron beam, it is more convenient to use two shunt capacitances C1 and C2, which relate to the areas adjacent to the impedance electrode from opposite sides. Such a SWS may be represented by a three-wire equivalent line with series inductance in the middle wire and shunt capacitances C1 and C2 connecting the middle wire with lower and upper wires, respectively (Figure 3). The use of electro-dynamic admittances of electric, Ye, and magnetic, Ym, types18 significantly simplifies calculation of the specific parameters of the three-wire equivalent line. As shown in,19 the equivalent capacitance C1 for the area below the impedance electrode, can be defined by the electric type admittance at the bottom surface of the impedance electrode,
C1=−2πaγ2jωYe1(a)
, (8)
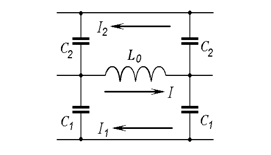
Figure 3 Three-wire equivalent line with specific inductance including the potential delay.
Whereas capacitance C2, related to the external (second) area, is
C2=2πaγ2jωYe2(a)
, (9)
Where in the considered case, a is the impedance electrode's radius. Here and further after, subscripts 1 and 2 are used to denote the internal and external areas, respectively. In the case of a planar electrode, the quantity 2πα in (8) and (9) should be replaced by the electrode’s width, whereas admittances in both cases should be taken on the impedance electrode surfaces. Although L can be split in two parallel inductances related to the different areas, in most cases it is more convenient to use one inductance defined by the jump of the magnetic-type admittances at the impedance electrode
L=2πajωh2[Ym2(a)−Ym1(a)]
(10)
According to definition,18
Ye1,2(a)=−Hϕ1,2(a)Ez1,2(a)
, (11)
Ym1,2(a)=Hz1,2(a)Eϕ1,2(a)
. (12)
For a planar impedance electrode, transverse coordinates r and ϕ should be replaced by x and y, respectively. Substituting (8)-(10) into (7), one can obtain the lossless version of the general dispersion equation derived in 18 for the helix with losses
(2πa)2ΔYeh2ΔYm+1=0
. (13)
Transition from a three-wire to a two-wire equivalent line is possible by adding together shunt capacitances, taking into account the difference in potential delays in the areas with different permittivity,19
C0=C1+γ21C2/γ22
, (14)
Where
γ21,2=β2−k2ε1,2
, (15)
and subscripts refer to different areas with relative permittivities ε1ανδε 2
Effective voltage
The peculiarity of all dispersive transmission lines is in the longitudinal capacitive (displacement) currents, which unlike the conduction currents in the electrodes, are subjected to smaller voltages than the voltage U between electrodes. This leads to a decrease in the power flow P as compared to the quantity UI/2. The conduction current passing through the screen electrode is only a part of the current in the impedance electrode, the rest being the longitudinal capacitive current. Equality of current amplitudes in the two-wire equivalent line is due to summing these currents. As a result, replacing transmission structures with longitudinal capacitive currents by equivalent lines leads to an incorrect definition of the power flow and, consequently, the wave impedance. Although the product L0C0, determined by formulas (8)-(10) gives correct dispersion equations, the ratio L0/C0 determining the wave impedance, is incorrect. As it was shown in,16 this problem may be solved by (1) introducing an effective voltage Uef, (2) reducing the equivalent inductance, and (3) increasing the equivalent capacitances. Voltage U at the impedance electrode and current I as well as the real power flow P may be found with help of expressions for components of the slow wave, obtained from solutions of the wave equations in the areas adjacent to the impedance electrode. For the same current and power flow in the equivalent line,
Uef=2P/|I|
, (16)
Where |I|
is the amplitude of the conduction current in the impedance electrode. We define the voltage correction coefficient Uef/U
as
ψ≡Uef/U
. (17)
The correction coefficient y is always less than 1. The decrease in Uef should be followed by a proportional decrease in L0 and L and the proportional increase in the shunt capacitance or capacitances. In the case of a two-wire truncated equivalent line, the equivalent series inductance and shunt capacitance are therefore:
Lef=ψL,Cef=C0/ψ
, (18)
It is seen that substitution of (17) and (18) in (7) does not change the dispersion equation, while the wave impedance can be defined unambiguously
Z0=UefI≡2PI2≡U2ef2P≡βγ√LefCef
. (19)
In the following section we demonstrate the application of these relations to the sheath helix in free space.
Free helix
The helix is the most frequently used and analyzed SWS. Even so, the published expressions for specific inductance and capacitance satisfying the transmission line dispersion equation do not satisfy the formulas for the wave impedance. Although in practice, the helix is used with a screen electrode; its diameter is chosen large enough to minimize its influence on the field in the helix. For the sake of simplicity we restrict our analysis to a helix in the absence of the screen electrode (free helix). The following formulas for specific inductance and capacitance and for power flow for the free helix had been derived previously:1,6,7,18
L=μ0tan2Φ2πI1(γa)K1(γa)
, (20)
C0=ε02πI0(γa)K0(γa)
, (21)
P=ωε0πβaA22γ3I0(γa)K0(γa)F(γa)
(22)
where I0,1 and K0,1 are the modified Bessel functions of the first and second kinds, zero and first orders, Φ is the angle between the direction of the helix conductivity and longitudinal axis, F(x) is an auxiliary function
F(x)=4x+I1(x)I0(x)−I0(x)I1(x)+K0(x)K1(x)−K1(x)K0(x)
, (23)
Whereas A is the constant in the formulas for the longitudinal components of the electric field intensity
Ez1(r)=AI0(γr)
, (24)
Ez2(r)=AI0(γa)K0(γa)K0(γr)
. (25)
The dispersion equation for the free helix can be found by substituting (20) and (21) in (7):
γ2k2=I1(γa)K1(γa)I0(γa)K0(γa)tan2Φ
. (26)
Equating the conduction current density to the jump of the azimuth components of the magnetic field intensity at the helix and multiplying by 2πα, one obtains the current
I=−2πAjωε0γ2K0(γa)
. (27)
The potential U at the helix can be obtained by integrating Ez2(r) from a to infinity,
U=−jβγ2Ez(a)=jβγ2AI0(γa)
. (28)
Substituting (22) and (27) into (16) gives the effective voltage
∣∣Uef∣∣=βaA4γI0(γa)F(γa)
. (29)
and
ψ=∣∣UefU∣∣=γa4F(γa)
. (30)
It follows from (18), (20), (21), and (30) that for the free helix
Lef=μ0tan2Φ8πγaI1(γa)K1(γa)F(γa)
, (31)
Cef=ε08πγaI0(γa)K0(γa)F(γa)
. (32)
Using (31) and (32) in (19) gives the formula for the wave impedance:
Z0=√μ0ε0βγγaF(γa)8πf(γa)tanΦ
, (33)
Where
f(γa)=√I0(γa)K0(γa)I1(γa)K1(γa)
. (34)
We also find that substitution of (27), (29) and (22) in the first three formulas of (19) gives
Z0=√μ0ε0γaN8πI0(γa)K0(γa)F(γa)
. (35)
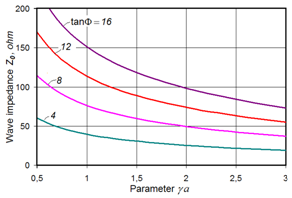
Figure 4 Wave impedance Z0 versus parameter γa for different values of angle Φ.
Equating the right hand sides of (33) and (35) leads to the dispersion equation (26), which confirms the equivalence of both expressions for the wave impedance. Figure 4 illustrates the dependence of the wave impedance on the dimensionless parameter γα calculated for the free helix for different values of Φ. It is seen that Z0 increases with the increase in Φ. It is obvious that in the presence of a solid cylindrical screen electrode the equivalent capacitance will increase and the equivalent inductance will decrease, producing a corresponding decrease in the wave impedance. This effect depends strongly on the value of γα, increasing with decreasing γα, i.e. with decreasing frequency, which in turn leads to a flattening the dependence of Z0 on frequency.
Calculation of the power flow by differentiation
In practice, when SWS has two or more cross-sectional areas, the calculation of the power flow is the most difficult part of the analysis. The same calculation is required for evaluation of the interaction impedance K1 and the coupling coefficient Kc,18 both values being used in the TWT theory for evaluation of the electron beam interaction with a slow wave. Being dimensionless, Kc is more convenient for practical application. In the case of a cylindrical beam tunnel with radius a filled by an electron beam18
Kc=ωε0πa22β0PA2[I20(γ0a)−I21(γ0a)]
, (36)
Where the power flow P is calculated by integrating the Pointing flux across the cross-section of the SWS, while the phase constant β0 and transverse constant γ0 are defined in the absence of the electron beam. It follows from (36) that
P=ωε0πa2A22β0I20(γ0a)−I21(γ0a)Kc
, (37)
That at known already Kc makes it possible calculating P. There are relatively simple methods for calculating Kc by differentiation the dispersion equation in the presence of the electron beam:18,20
Kc=γ20β20(∣∣dTdγ∣∣γ0−1)−1
. (38)
Here T is the transverse constant in the electron beam and γ is the "disturbed" by the beam transverse constant in free from the electrons areas. This gives for the free helix interacting with the electron beam with radius α:
Kc=τ20β20I20(γ0a)−I21(γ0a)I0(γ0a)K0(γ0a)F(γ0a)γ0a]
. (39)
For the free helix, the coupling coefficient was defined with the help of formula (36) in the monograph.18 The substitution (39) in (37) gives an expression for P identical to that obtained in1 and18 by integration the power flow density.
Discussion
A method of replacing the slow-wave structure by an equivalent transmission line with parameters providing unambiguous determination of the wave impedance was found and described. The method is based on the introduction of an equivalent voltage that yields the correct value of power flowing for the real value of the conduction current. It is shown that the decrease in the equivalent inductance and simultaneous increase in the equivalent capacitance, proportional to the decrease in the equivalent voltage, provides an unambiguous definition of the wave impedance. The decrease in the equivalent voltage is defined by the decrease in the real power flow, caused by the longitudinal capacitive currents.
It is demonstrated also that the unambiguous determination of the wave impedance of slow-wave structures can be simplified by differentiation of the dispersion equation in the presence of a homogeneous electron beam.
Acknowledgements
The author wishes to thank Dr. David Chernin of Leidos for editorial and English grammar assistance.
Conflict of interest
The author declares no conflict of interest.
References
- JR Pierce. Traveling Wave Tubes Prinston. Van Nostrand, NJ, USA; 1950.
- Lebedev IV. Microwave Technology and Devices. Vysshaya Shkola, Moscow, Russia; 1970.
- Collin RE. Foundations for Microwave Engineering. USA: McGraw–Hill Book Company; 1992.
- Neiman MS. Generalizing the circuit theory on the waveguides. Gosenergoizdat, Moscow, Russia; 1955.
- Brown RG, Sharpe RA, Hughes WL, et al. Lines, Waves, and Antennas. The Transmission of Electric Energy. 2nd ed. USA: John Wiley & Sons; 1973.
- Silin RA, Sazonov VP. Slow–Wave Structures. Sovradio, Moscow, Russia; 1966.
- Pike SF. Design formulas for helix dispersion shaping. IEEE Transactions on ED. 1969;16(12):1010–1014.
- Yu N Pchelnikov. Relationship between the wave impedance and the coupling resistance of slow–wave structures. Radiotekhnika i Electronika. 1983;28(10):1981–1985.
- Gilmour S. Principles of raveling Wave Tubes Boston London: Artech House, London, UK; 1994.
- Carter RG, Wang P. An equivalent circuit model for helix slow–wave structures. Proc Conf Microwaves. 1994:94.
- Watkins DA. Topics in Electromagnetic Theory. USA: John Willy & Sons Inc; 1958.
- Yu N Pchelnikov. Features of slow–waves and potentials for their nontraditional application. Journal of Communication Technology and Electronics. 2003;48(4):450–462.
- Pchelnikov Yu N, Kholodnyi VA. Medical Application of Surface Electromagnetic Waves. Bioelectrochemistry and Bioelectronics. 1988;47(2):283–290.
- Yu N Pchelnikov, Nyce DS. Slow–wave structures based method of measurements. IEEE Trans on Instrum Measur. 2002;51(5):891–896.
- Yu N Pchelnikov. Sensitive element on cross–wound helices. IEEE Sensors Journal. 2017;17(9):1–7.
- Yuriy N Pchelnikov. Determination of equivalent parameters of waveguides with circular and rectangular cross sections. Journal of Communication Technology and Electronics. 2010;55(1):106–111.
- Yu N Pchelnikov, Ye V Zykova, N Ye Ivanova. On a procedure for determining the parameters of equivalent circuits. Radiotekhnika i Electronikas. 1980;25(6):1231–1237.
- Loshakov LN, Yu N Pchelnikov. Theory and Gain Calculation of Traveling Wave Tube. Sovradio, Moscow; 1964.
- Yu N Pchelnikov. On the replacement of slow–wave systems by a three–conductor equivalent line. Journal of Communication Technology and Electronics. 1994;39(9):68–74.
- Yu N Pchelnikov. Calculation of the coupling coefficient of electron beam in TWTs using parameters of equivalent line. Journal of Communication Technology and Electronics. 2010;55(2):215–220.

©2017 Pchelnikov. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


