
Technical Paper Volume 2 Issue 2
Exact solutions of one problem of nonlinear theory of elasticity for two potentials of energy of incompressible material
Andreeva Julia Yuryevna, Zhukov Boris Alexandrovich
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Volgograd State Technical University, Volgograd
Correspondence: Zhukov Boris Alexandrovich, Volgograd State Technical University, Volgograd State Social and Pedagogical University, Volgograd
Received: December 11, 2017 | Published: April 16, 2018
Citation: Yuryevna AJ, Alexandrovich ZB. Exact solutions of one problem of nonlinear theory of elasticity for two potentials of energy of incompressible material. Aeron Aero Open Access J. 2018;2(2):88-93. DOI: 10.15406/aaoaj.2018.02.00036
Download PDF
Abstract
In the nonlinear theory of elasticity, which is an apparatus for the study of rubber-like materials, at present there is no single equation of state for such materials, similar to Hooke's law in linear theory. The development of new rubber-like materials, the study of various biological materials leads to the need to create new models of response to external influences. In the framework of hyper elasticity, this leads to the appearance of new mathematical expressions for the deformation energy potential. In commercial packages designed to calculate the stress-strain state of structures from elastomers, the expressions for the deformation energy potential are rather rigidly defined. To accommodate new models, you have to create new application packages. Their verification is carried out using known exact solutions. In this paper, two exact solutions of one model problem for deformation energy potentials proposed by Fung1 and Gent et al.2, for which we could not find solutions in the literature. The practical significance of exact solutions is not limited to their application for the verification of numerical methods; they allow one to investigate effects not described by linear theory. It is shown that the difference in potentials leads not only to quantitative, but also to qualitative difference of solutions.
Keywords: final cylindrical deformation, hyper elastic incompressible material, deformation energy potentials, exact solutions
Introduction
The notation and terminology of the article follow the adopted in.3 Rubber is a unique structural material, due to which it has a lot of engineering applications.4 It has a high elasticity in a wide range of temperatures, resistance to aggressive media and hard radiation, which can be used as seals in space vehicles, chemical production. It has excellent damping properties, which contributes to use as shock absorbers, in particular cylindrical shock absorbers. Rubbers are used in the manufacture of solid fuels and in biomechanics. Biological materials5 have similar properties (high elasticity), therefore, rubber is widely used in prosthetics. Precise prediction of the mechanical behavior of rubber is an important task that is still far from full understanding. At the moment, many models are known which are in good agreement with experiment in one type of loading and poorly with another for specific materials. In6, 32 known models of hyper elastic isotropic incompressible materials are presented and new ones are proposed. In7 one can find 12 more models not mentioned in.6 Therefore, it is important to find exact solutions within the framework of different potentials for a reliable study of the properties of materials modeled by these potentials. Since the problem of antiplane deformation is one of the simplest, a lot of work has been devoted to it both by domestic and foreign authors. The results are outlined in the chapters of the monographs.8-10 We note that for incompressible materials a finite antiplane deformation is possible only in bodies with deformation energy potentials satisfying the conditions formulated.
It is always possible in materials with a generalized Neo-Hukonian potential. For potentials of the type, antiplane deformation is possible, for example, in the material of Mooney-Rivlin and some others. Here are the principal invariants of the right Cauchy-Green deformation tensor. In the general case, a cylindrical deformation is realized,11 that is, a complex of flat and antiplane deformations. The planar deformation acts in the transverse plane for the antiplane deformation of the plane. If external factors for plane deformation are absent, and it appears as a reaction to an antiplane shift, then it is called latent.12 If flat deformation is forbidden kinematically (as in shock absorbers), then a flat stress field appears.13,14 A review of the state of studies of finite antiplane deformation up to 1995 is contained in.15 A systematic investigation of the finite antiplane deformation begins with the works of Knowles JK.16-23 More recent works are associated with the names Gao,24,25 Hayes et al.26, Polignone et al.27, Pucci et al.28 Cylindrical deformation was considered in.13,14 In the present paper, two solutions are given, one for a material with a generalized non-wick potential deformation energy,1 for which the latent stress field in the transverse plane does not occur, and for a material with potentials,2 in which such a field arises. The effect of the latent stress field on the concentration of the deformation energy potential is discussed.
Statement of static problems for finite cylindrical deformation
The general statement of the problems of nonlinear elasticity is reduced to a form convenient for further consideration.11 We orient the spatial Cartesian coordinate system so that the radius vectors of the points in the current and reference configurations, respectively, have the form:
(1.1)
where
- coordinates of points in the reference configuration, selected as material.
- basis of the spatial Cartesian coordinate system. Expressions (1.1) ensure that the deformation is anti-flat.
Following,8 the stress state of a homogeneous isotropic hyper elastic incompressible material with a deformation energy potential
can be described with the aid of the Cauchy tensor of the true stresses
in the form:
s (1.2)
Across
denotes the unit tensor,
-the hydrostatic pressure function
is the Hamiltonian operator in the reference configuration.
The principal invariants of the right Cauchy-Green deformation tensor are obtained in the form:
(1.3)
Equilibrium equations in the absence of mass forces will be written in the form:
(1.4)
Eliminating the hydrostatic pressure function in the first equation from (1.4), we obtain
(1.5)
Thus, the strain energy potential must ensure the consistency of the second equation in (1.4) and equation (1.5). The conditions for choosing the potential are given in.16 It is obvious that these conditions are satisfied by the generalized Neo-Hooke potential, since for it
.
When cylindrical deformation (including anti-flat), the cylindrical lateral surface again passes into a cylindrical surface with a unit vector of the normal <
, so the force boundary condition on the lateral surface
will be written in the form:
(1.6)
(1.7)
Here, the density of external forces
/>is calculated per unit area of the lateral surface in the deformed state (for an antiplane deformation, the area of the lateral surface does not change). In expression (1.6), the quantity
gives the density of external forces in the transverse plane necessary to maintain the regime of antiplane deformation. If this regime is maintained kinematically, then the force density
manifests itself as a reaction from the rigid clips, between which a deformable cylindrical body is enclosed. In the case of a generalized Neo-Hooke potential, the function is assumed to be zero and there are no stresses in the transverse plane. The kinematic boundary conditions reduce to setting the longitudinal shear on the outer lateral surface.
Model problem of the finite longitudinal displacement of a circular cylindrical sleeve between rigid concentric rings
As a problem for which exact solutions are sought, the problem of the finite longitudinal shear of a circular cylindrical sleeve between rigid concentric rings is considered. On the one hand, this is one of the simplest tasks, on the other hand it has an applied value, since it is one of the designs of a shock absorber. The inner cage is stationary, and the outer casing is shifted along the symmetry axis by
. The counting and deformed sleeve configurations are shown in Figure 1.
As material we will use the coordinates of the cylindrical coordinate system
with a unit basis:
,
,
;and an axis directed along the axis of symmetry of the sleeve. The Hamilton operator in this basis is obtained in the form:
. In this case, the antiplane deformation is also axisymmetric, that is
and,
Thus, the expressions (1.1) - (1.4) go over into the following (the prime denotes the derivative with respect to
:,
, (2.1)
(2.2)
< p>Equation (1.5) is a consequence of the second equation in (2.2), that is, an axisymmetric version of the antiplane deformation exists for any deformation energy potential.
The kinematic boundary conditions are written in the form:
(2.3)
We find the first integral of the second equation in (2.2):
(2.4)
The unit vector of the outer normal to the outer lateral surface of the sleeve with equation
equals , therefore, the shearing force calculated per unit length of the sleeve according to (1.7), (2.1) and (2.4) is obtained as:
Hence
. Thus, we obtain:
In what follows we turn to dimensionless quantities:
The correspondence of the notation for the derivatives is obtained in the form:
With these relations in mind, the expression for the shear stress can be rewritten
(2.5)
Expression (2.5) does not depend on the deformation energy potential and coincides with the solution of the linear theory.
If it is necessary to find the stress state in the transverse plane, the hydrostatic pressure function is found from the first equation in (2.2):
The dimensionless integration constant
is found from the condition that the principal vector on the end surface vanishes. Since the transverse plane is deplanated in the case of an antiplane deformation, it is easiest to take into account the vanishing of the principal vector in this plane by means of the first Piola-Kirchhoff
, stress tensor obtained from the Cauchy tensor by using the relation
, written for an incompressible material. The vector of the unit normal to the cross section in the reference configuration is the vector , therefore we have:
(2.6)
We obtained an equation for finding.
Equation (2.4) can be rewritten in the form
(2.7)
This non-linear differential equation is used to find the cross-sectional de-planing function
.
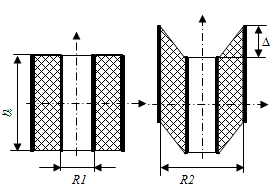
Figure 1 The counting and deformed sleeve configurations.
Choice of models of isotropic incompressible hyper elastic material
This problem was solved by many authors for various potentials.29 Let us dwell on some potentials from,1 for which we could not find a solution in the literature. Since for homogeneous first-order materials
and
are functions of only
some parameters, when substituting a specific expression for the deformation energy potential into equation (2.7), it becomes an algebraic or transcendental equation with respect to
. The success in obtaining an explicit expression for an exact solution
depends on the possibility of obtaining an explicit expression for solving this equation with respect to
. Obtaining such a solution is always possible for algebraic equations of degree not higher than the fourth. For transcendental equations, obtaining explicit expressions for solving is problematic.
Solution for potential [1]
Here and below is the shear modulus of the linear theory of elasticity. Although the equation (2.7) for the potential [1]
,
:
(3.1);
it is not less than that, the solution of the differential equation is found and expressed through the function of Lambert30 and the exponential integral
(3.2)
This verification is verified by the direct substance (3.2) in (3.1). For the connection I take a relationship30
,
.
From (3.2) we obtain the hardness curve of the resinometallic amortizator
(3.3)
For
potential [1] it is aimed at the non-zero potential
, and the expression (3.3) is about to be known
. Figures 2 are represented by curves (3.3) for
(curve 1) and
(curve 2). The linear direct corresponds to the non-zero potential in all cases
. It is clear that the dependencies are non-linear and approach with decrease
to the non-dependent dependence of the lower; they are described by more severe materials.
Poskol'ku potential [1] relates to the class of generalized non-magnetic potentials, this voltage state does not drive in the transverse plane. Introducing interest is a consideration of the potential, which depends on both main algebraic invariants .In this case, a field of voltage is applied in the lateral plane.
Solution for potential [2]
The expression for the potential has the form:
brought into forms, for which the equation of state with this potential in small deformations is transferred to the Guka law.
Correlation (2.7) for the potential [2] is equivalent to the third-order algebraic equation relative to :
The following equation has significant coefficients, that is to say, whether it is three important corners, whether two complexally connected and one of the pure root. In our case for values
the second option is implemented. The only real root is:
(3.4)
By (3.4) there is an expression for
and a rigid curve amortizator (dependence from)
(3.5)
When
the potential [2] tends to the Neo-Hooke potential. Figure 3 shows the curves (3.5) for
curve 1) and
(curve 2). The shaded line corresponds to the Neo-Hooke potential. In all cases
. It can be seen that the non-linear dependences approach the decrease
to the Neo-Hukonian dependence from above, that is, they describe the softer materials.
It is of interest to compare the distribution of tangential stresses
that are not taken into account by the linear theory, with shear stresses from longitudinal shear .
For the potential [2]
and equation (2.6) can be rewritten in the form
(3.6)
Substituting (3.4) into (3.6) we obtain an expression for finding,that is not given because of the unwieldiness.
For example, Figure 4 shows the dependences
of
for
(curve 1) and
(curve 2). In both cases .
For the tangential stress,
(3.7)
Substituting (3.4) into (3.7) we obtain the final expression. Figure 5 shows the distributions of the relative stresses
c(curve 1) and
(curve 2) for
and . It is seen that the concentration of tangential stresses is quite comparable to the concentration of tangential stresses, although lower.
Figure 6 shows the distribution of the specific energy of deformation energy
across the cross section of the sleeve, for
and different
. At
(Neo-Hooke potential) we have curve 1. In this case, there is no latent stress field in the transverse plane. The values of
and
correspond to curves 2 and 3. It is seen that with increasing transverse stress field not taken into account by the linear theory of elasticity, the concentration of the deformation energy potential increases and exceeds the corresponding values for the Neo-Hooke potential. This may be important, since there are experimental data31 that the destruction of rubber products does not begin in the zones of maximum stresses, but in the zones of maximum values of the deformation energy potential.
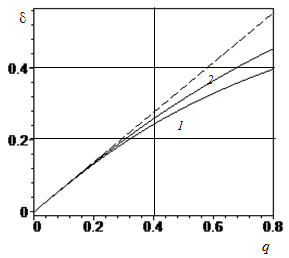
Figure 2 Representation of curves (3.3) for
(curve 1) and
(curve 2).
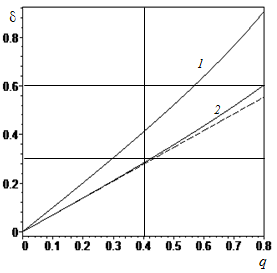
Figure 3 Representation of curves (3.5) for
(curve 1) and
(curve 2).
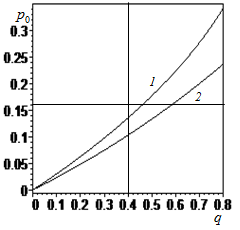
Figure 4 The dependences
of
for
(curve 1) and
(curve 2).
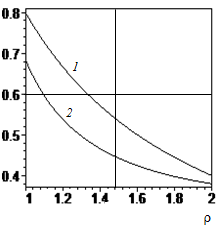
Figure 5 The distributions of the relative stresses
(curve 1) and
(curve 2) for
and.
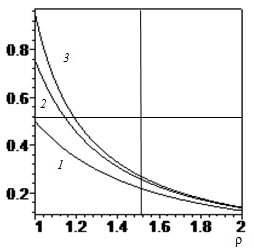
Figure 6 The distribution of the specific energy of deformation energy
across the cross section of the sleeve, for
and different
.
Conclusion
New exact analytical solutions of one problem of nonlinear elasticity theory for two strain energy potentials of incompressible material are obtained. As a model, the well-known problem of the antiplane axisymmetric deformation of a cylindrical sleeve between rigid concentric rings was considered. The nonlinear effect of the stress state in the transverse plane under the action of a finite longitudinal shear is investigated; its effect on the concentration of the deformation energy potential is elucidated.
Acknowledgement
Conflicts of Interest
References
- Fung YCB. Elasticity of soft tissues in sample elongation. Am J Physiol. 1967;213(6):1532‒1544.
- Gent AN, Thomas AGJ. Polymer Science. 1958;28:625.
- Truesdell C, Noll W. The Non-linear Field Theories of Mechanics. Newyork: Springer; 2003. 602p.
- Badenkov PF, Evstratov VF, Reznikovsky MM. Rubber is a structural material of modern engineering. Moscow: Chemistry; 1967. 324p.
- Giampaolo M, Thomas CG, Jehangir JA, et al. Mechano-biology in the thoracic aortic aneurysm: a review and case study. Biomech Model Mechanobiol. 2014;13(5):917‒928.
- Hossa L, Marczak RJ. A new constitutive model for rubber-like materials. Computational Mechanics. 2010;29(28):2759‒2773.
- Chernykh KF, Shubina IM. Laws of elasticity for isotropic incompressible materials, phenomenological approach. Mechanics of elastomers. Krasnodar. 1977;1(242):54‒64.
- AI Lur'e. Nonlinear theory of elasticity. Moscow: Nauka; 1980. 512p.
- Chernykh KF, Litvinenkova ZN. Theory of large elastic deformations. Leningrad: Izd-vo LGU; 1988. 254 p.
- Antman SS. Nonlinear Problems of Elasticity. Springer-Verlag: New York; 2005. 835p.
- Zhukov BA. Nonlinear interaction of finite longitudinal shear with finite torsion of a rubber-like bushing. Mechanics of solids. 2015; 50(3):337‒344.
- De Pascalis R, Destrade M, Saccomandi G. The stress field in a pulled cork and some subtle points in the semiiinverse method of nonlinear elasticity. Proc Royal Soc A. 2007; 463(2087):2945.
- Zhukov BA. Nonlinear effect of the interaction of flat and antiplane deformations in an incompressible material // Modern problems in the mechanics of a continuous medium. 4th International conference: Rostov; 1998. 142–145p.
- Horgan С, Saccomandi G. Superposition of generalized plane strain on anti-plane shear deformations in isotropic incompressible hyperelastic materials. Journal of Elasticity. 2003;73(1-3):221–235.
- Horgan CO. Anti-Plane Shear Deformations in Linear and Nonlinear Solid Mechanics. SIAM Review. 1995;37(1):53–81.
- Knowles JK. On finite anti-plane shear for incompressible elastic materials. The Journal of the Australian Mathematical Society. Series B. Applied Mathematics. 1976;19(4):400–415.
- Knowles JK. A note on anti-plane shear for compressible materials in finite elastostatics. The Journal of the Australian Mathematical Society. Series B. Applied Mathematics. 1977;20(1):1–7.
- Knowles JK. The finite anti-plane sheared near the tip of a crack for a class of incompressible elastic solids. Int J Fracture. 1977;13(5):611–639.
- Knowles JK. A note on the spatial decay of a minimal surface over a semi-infinite strip. J Math Anal Appl. 1977;59(1):29–32.
- Knowles JK. Universal states of finite anti-plane shear: Erickson’s problem in miniature. Amer Math Monthly. 1979;86:109–113.
- Knowles JK, Rosaki AJ. On the scale of the nonlinear effect in a crack problem. J Appl Mech. 1986;53(3):545–549.
- Knowles JK. Sternberg E. Discontinuous deformation gradients near the rip of a crack in finite anti-plane shear: An example. J Elasticity. 1980;10(1):81–110.
- Knowles JK, Sternberg E. Anti-plane shear fields with discontinuous deformation gradients near the tip of a crack in finite elastostatics. J Elasticity. 1981;11(2):129–164.
- Gao DY. Analytical Solutions to General Anti-Plane Shear Problems In Finite Elasticity. Continuum Mech Thermodyn. 2016;28(1-2):175–194.
- Gao DY. Remarks on Analytic Solutions in Nonlinear Elasticity and Anti-Plane Shear Problem. Mathematical Physics. 2015; 17p.
- Hayes MA, Saccomandi G. Antiplane shear motions. Quarterly Journal of Mechanics and Applied Mathematics. 2004;57(3):379–392.
- Polignone DA, Horgan CO. Axisymmetric finite anti-plane shear of compressible nonlinearly elastic circular tubes. Quarterly of Applied Mathematics. 1992;1(2):323–341.
- Pucci E, Saccomandi G. The Anti-Plane Shear Problem in Nonlinear Elasticity Revisited. J Elasticity. 2013;113(2):167–177.
- Kanner LM, Horgan CO. Inhomogeneous shearing of strain-stiffening rubber-like hollow circular cylinders. International Journal of Solids and Structures. 2008;45(20):5464–5482.
- Valluri SR, Jeffrey DJ, Corless RM. Some applications of the Lambert W function to physics. Can J Phys. 2000;78(9):823–831.
- Bokin DP, Korostelev SA, Nechaev KS. Determination of the beginning of the destruction of the rubber element rubber-metal hinge caterpillar propulsion. Vestnik of the Altai State Agrarian University. 2009;7(57):61–65.

©2018 Yuryevna, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


