Optimization of intersecting straight lines methods for the evaluation of acidity constants of single equilibria from spectrophotometric data

doi:10.15406/ppij.2018.06.00197

eISSN: 2379-6367

Pharmacy & Pharmacology International Journal

Research Article Volume 6 Issue 4

Optimization of intersecting straight lines methods for the evaluation of acidity constants of single equilibria from spectrophotometric data

Julia Martin,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Agustin G Asuero,² M Angeles Herrador,² Gustavo Gonzalez³

¹Department of Analytical Chemistry, Escuela Politecnica Superior, University of Seville, Spain
²Department of Analytical Chemistry, Faculty of Pharmacy, University of Seville, Spain
³Department of Analytical Chemistry, Faculty of Chemistry, University of Seville, Spain

Correspondence: Julia Martin, Department of Analytical Chemistry, Escuela Politecnica Superior, University of Seville, C/ Virgen de Africa, 7, E-41011 Seville, Spain, Tel 34-9-5455-6250

Received: July 12, 2018 | Published: August 30, 2018

Citation: Martín J, Asuero AG, Herrador MA, et al. Optimization of intersecting straight lines methods for the evaluation of acidity constants of single equilibria from spectrophotometric data. Pharm Pharmacol Int J. 2018;6(4):333-338. DOI: 10.15406/ppij.2018.06.00197

Download PDF

Abstract

The acid dissociation constant (K_a) is among the most frequently used physicochemical parameters, and its determination is of interest to many research fields. A number of graphical methods has been proposed for the spectrophotometric evaluation of acidity constants of single equilibrium HR=H+R (charges omitted for the sake of generality), in those cases in which the limit absorbance’s of the pure species HR or R, A₁ and A₀, respectively, are unknowns. The raw values of absorbance’s versus pH data are transformed in linear functions, which allow to evaluate the unknown parameter K_aand A₀/or A₁ by a graphical approach or by the application of the least squares method. Among the various methods proposed the double reciprocal, Agren-Sommer and Nash methods yield to a family of intersecting straight lines when experimental measurements of absorbance and pH are made at different wavelengths. The purpose of this paper is to critically examine these methods on the basis of the requirements of single linear regression.

Keywords: intersecting straight lines methods, acidity constants, spectrophotometric data

Introduction

Among the physico-chemical properties of molecules, the acidity constants are of vital importance both in the analysis of drugs as well as in the interpretation of their mechanism of action.^1–4The solution of many galenical problems requires the knowledge of the acidity constants of compounds⁴ of pharmaceutical interest. Many compounds of biological interest have acidity constants, which lie close to each other. Their absorption, further transport and effect in the living organism are affected by the ratio of concentration of protonated and non-protonated forms in various media. Thus, the knowledge of acidity constants is worthy. The evaluation of acidity constants of organic reagents is also of great value to plan analytical experiments,⁵ e.g., the acidity constants can be employed in the design of titration procedures⁶ and to examine the likelihood of separation of mixtures of compounds by extraction.

Although black-box computer software’s are easily available nowadays, the spectrophotometric determination of equilibrium constants⁷ of single equilibria, such as acidity constants (K_a) of monoprotic acids by graphical plots seems to be valuable, due to the transparency of the linearized methods applied. Spectrophotometry is the choosen method when pK_a values are either enough high or low and/or solubility problems⁸ appear. The correct evaluation of pK_a of substances of therapeutic interest has vital importance in drug analysis and for the interpretation of their mechanisms of action. A number of graphical methods has been proposed⁹ for the spectrophotometric evaluation of acidity constants, HR=H+R (charges omitted for the sake of generality) in those cases in which the limit absorbance of the pure species HR, A₁, or R, A₀, are unknown. Among them, the double reciprocal or Maroni-Calmon,¹⁰ Agren-Sommer^11–12and Nash¹³ methods, lead to a family of intersecting straight lines when experimental measurements of absorbance and pH are made at varying wavelengths.

In these classical spectrophotometric methods the experimental absorbance pH curves are linearized. For the straight lines (Y=a₀+a₁ X) obtained in each case by the least squares method, we may easily evaluate the unknown parameters, that is, the acidity constant K_a, and the unknown absorbance, A₀ or A₁, from the slope, a₁, and the intercept, a₀, of the corresponding lines. The expressions applied in the available methods as well as the calculations of K_a values are shown in Table 1. If the A-pH measurements are made at different wavelengths a set of intersecting straight lines is obtained, given the coordinates of the cut-off points included (summarized) in Table 2. The purpose of this paper is to shown which of the three methods is more appropriate for linear regression analysis.

Method	Known absorbance limit	Expression	X	Y	Ka
Agren-Sommer	A₀	$Y = \frac{1}{A_{1}} + \frac{K_{a}}{A_{1}} X$	$\frac{A - A_{0}}{A [H^{+}]}$	$\frac{1}{A}$	$\frac{b}{a}$
Agren-Sommer	A₁	$Y = \frac{1}{A_{0}} + \frac{1}{A_{0} K_{a}} X$	$\frac{A - A_{1}}{A} [H^{+}]$	$\frac{1}{A}$	$\frac{a}{b}$
Maroni-Calmon	A₀	$Y = \frac{1}{A_{1} - A_{0}} + \frac{K_{a}}{A_{1} - A_{0}} X$	$\frac{1}{[H^{+}]}$	$\frac{1}{A - A_{0}}$	$\frac{b}{a}$
Maroni-Calmon	A₁	$Y = \frac{1}{A_{0} - A_{1}} + \frac{1}{(A_{0} - A_{1}) K_{a}} X$	$[H^{+}]$	$\frac{1}{A - A_{1}}$	$\frac{a}{b}$
Nash	A₀	$Y = \| \frac{A_{0} - A_{1}}{A_{0}} \| \frac{1}{K_{a}} X - \frac{1}{K_{a}}$	$\frac{1}{1 - \frac{A}{A_{0}}}$	$\frac{1}{[H^{+}]}$	$- \frac{1}{a}$
Nash	A₁	$Y = \| \frac{A_{1} - A_{0}}{A_{1}} \| K_{a} X - K_{a}$	$\frac{1}{1 - \frac{A}{A_{1}}}$	$[H^{+}]$	- $a$

Table 1 Expressions used according to various methods and other parameters of interest

Method	Limit absorbance	Intersecting point
Agren-Sommer and Maroni-Calmon	A₀ known	(-1/K_a, 0)
Agren-Sommer and Maroni-Calmon	A₁ known	(-K_a, 0)
Nash	A₀ known	(0, -1/K_a)
Nash	A₁ known	(0, -K_a)

Table 2 Coordinates of intersecting points in when measurements are made at varying wavelengths

Theory

The correct use of the least squares method requires^14–15several assumptions when it is applied to linear regression analyses:

The measurement of the variable X is assumed error-free.
The Y values obtained (replicates) for the same X value must show a Gaussian distribution.
The standard deviation of the Y values should not change in the range of values covered by the X values (homocedasticity).

If the various expressions proposed in Table 1 are examined in this regard, it can be accepted in the first instance that conditions b) and c) are met, but not a). Given the different nature of the mathematical function that relates the variables of regression X and Y with the experimental values of A and pH in each method, condition a) should be checked through the propagation of errors made in the mean values of A and pH over the various pairs of data X, Y object of the regression.

Error analysis

Let z be a function of the variables A and pH, z=f(A, pH). The errors involved in the measurement of A and pH will be propagated through Z according¹⁶ to the random error propagation law

$s_{z} = {(\frac{\partial z}{\partial A})}^{2} s^{2}_{A} + {(\frac{\partial z}{\partial p H})}^{2} s^{2}_{p H}$ (1)

where s_A² and s_pH² are the variances (squared standard deviations) of the absorbance and pH, respectively. Measurements of A and pH are independent, and then cov(A, pH)=0. The application of the Eqn. (1) to the expression of the three methods tested is compiled in Table 3.

Method	Known absorbance limit	Variance of variables
Agren-Sommer	A₀	$\begin{array}{l} S_{Y}^{2} = S_{A}^{2} / A^{4} \\ S_{X}^{2} = A_{0}^{2} S_{A}^{2} / (A^{4} {[H^{+}]}^{4}) + {(A - A_{0})}^{2} \ln^{2} 10 S_{p H}^{2} / (A^{2} {[H^{+}]}^{2}) \end{array}$
Agren-Sommer	A₁	$\begin{array}{l} S_{Y}^{2} = S_{A}^{2} / A^{4} \\ S_{X}^{2} = {[H^{+}]}^{2} A_{1}^{2} S_{A}^{2} / A^{4} + ({(A - A_{1})}^{2} / A^{2}) \ln^{2} 10 {[H^{+}]}^{2} S_{p H}^{2} \end{array}$
Maroni-Calmon	A₀	$\begin{array}{l} S_{Y}^{2} = S_{A}^{2} / {(A - A_{0})}^{4} \\ S_{X}^{2} = \ln^{2} 10 S_{p H}^{2} / {[H^{+}]}^{2} \end{array}$
Maroni-Calmon	A₁	$\begin{array}{l} S_{Y}^{2} = S_{A}^{2} / {(A - A_{1})}^{2} \\ S_{X}^{2} = {[H^{+}]}^{2} \ln^{2} 10 S_{p H}^{2} \end{array}$
Nash	A₀	$\begin{array}{l} S_{Y}^{2} = \ln^{2} 10 S_{p H}^{2} / {[H^{+}]}^{2} \\ S_{X}^{2} = {A_{0}^{2} S_{A}^{2} / (A_{0} - A)}^{4} \end{array}$
Nash	A₁	$\begin{array}{l} S_{Y}^{2} = {[H^{+}]}^{2} \ln^{2} 10 S_{p H}^{2} \\ S_{X}^{2} = {A_{1}^{2} S_{A}^{2} / (A_{1} - A)}^{4} \end{array}$

Table 3 Propagation of errors in the different variables

If it is assumed that s_A and s_pH have the values of 0.001 and 0.01, respectively, given the precision of common spectrophotometers and pH-meters, we may evaluate the standard deviation of the variables X and Y, s_X and s_Y, respectively, by using five series of synthetic absorbance versus pH data, with 21 points uniformly distributed in the pH range pK_a±1, applying the Monte Carlo method, detailed e.g. in reference.¹⁷ The results obtained from this study, expressed as relative standard deviations s_X/X and s_Y/Y are shown in Table 4.

Method	Known absorbance limit $S_{Y} / Y$ $S_{X} / X$
Agren-Sommer	A₀	$(2 - 1.4) \cdot 10^{- 3}$	$0.023$
Agren-Sommer	A₁	$(2.1 - 1.4) \cdot 10^{- 3}$	$(0.02 - 0.01)$
Maroni-Calmon	A₀	$(4 - 2) \cdot 10^{- 3}$	$0.023$
Maroni-Calmon	A₁	$(3 - 1) \cdot 10^{- 3}$	$0.023$
Nash	A₀	$0.023$	$(4 - 2) \cdot 10^{- 3}$
Nash	A₁	$0.023$	$(2 - 1) \cdot 10^{- 3}$

Table 4 Relative precision of the different regression variables

Transformation of Expressions

It can be seen from results included in Table 4 that the method of Nash led to a greater precision in the measurement of the variable X compare to the other two methods. If we are interesting in applying both Agren-Sommer and Maroni-Calmon method in a more rigorous way, the role of the variables X and Y must be interchanged leading to the expressions found in Table 5. An additional advantage of the transformed expressions is that allow a simple calculation of the standard deviation of Ka values

$s_{K}_{_{a}} = | \frac{\partial K_{a}}{\partial a_{0}} | s_{a_{0}}$ (2)

because the acidity constant coincides with the intercept (A₀ known) or the reciprocal intercept (A₁ known) of the corresponding straight line obtained.

By using the classical expressions we obtain instead more complex relationships for the standard deviation of Ka

$s^{2} {_{K}}_{_{a}} = {(\frac{\partial K_{a}}{\partial a_{0}})}^{2} s^{2}_{a_{0}} + {(\frac{\partial K_{a}}{\partial a_{1}})}^{2} s^{2}_{a_{1}} + 2 (\frac{\partial K_{a}}{\partial a_{0}}) (\frac{\partial K_{a}}{\partial a_{1}}) cov (a_{0}, a_{1})$ (3)

However, by using the new expressions proposed with the synthetic data generated, smaller standard deviations values are obtained (approximately half) than by applying the classical equations. To illustrate the above, a practical application has been developed.

Method	Known absorbance limit	Expression	X	Y	Ka
Agren-Sommer	A₀	$Y = \frac{1}{A_{1}} + \frac{K_{a}}{A_{1}} X$	$\frac{1}{A}$	$\frac{A - A_{0}}{A [H^{+}]}$	$- \frac{1}{a}$
Agren-Sommer	A₁	$Y = \frac{1}{A_{0}} + \frac{1}{A_{0} K_{a}} X$	$\frac{1}{A}$	$\frac{(A - A_{1}) [H^{+}]}{A}$	$- a$
Maroni-Calmon	A₀	$Y = \frac{1}{A_{1} - A_{0}} + \frac{K_{a}}{A_{1} - A_{0}} X$	$\frac{1}{A - A_{0}}$	$\frac{1}{[H^{+}]}$	$- \frac{1}{a}$
Maroni-Calmon	A₁	$\begin{array}{l} Y = \frac{1}{A_{0} - A_{1}} + \frac{1}{(A_{0} - A_{1}) K_{a}} X \end{array}$	$\frac{1}{A - A_{1}}$	$[H^{+}]$	$- a$

Table 5 Transformed expressions for the Agren-Sommer and Maroni-Calmon methods

Materials and methods

In this paper a pH meter CRISON model 501pH meter with combined glass-Ag/AgCl electrodes (In gold) with a range of use of 0 to 14pH units, has been used in pH measurements. A Spectrophotometer SPECTRONIC 2000 (Bausch & Lomb) provided with a graphic XY recorder and equipped with quartz cells of 1-cm path-length has been used for absorbance measurements.

The two classical methods as well as the new expressions have been applied to the pKa evaluation of the methylglyoxal bis (4-phenyl-3thiosemicarbazone) (MGBPT).^18–19 Although this reagent has two close pKa corresponding to the equilibria of the type expressed in the following scheme²⁰

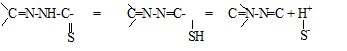
applying the Coleman or Polster methods1,21–23 it can be shown that in the range of about 10-12pH, the two species corresponding to the first ionization equilibrium are found from a practical point of view.

To obtain the A-pH curves of the reagent, solutions of MGBPT concentration equal to 1.0810-5M are prepared in 25-mL volumetric flasks. The appropriate pH is achieved by adding different volumes of KOH or HCl of various concentrations. To ensure the homogeneity of the solutions, N-N'-dimethylformamide (DMF) is added (the optimum solvent for this reagent is a mixture of DMF and water) so that the samples have 60% V/V of DMF. To fix the ionic strength of the medium in 0.1, 2.5ml of solution of KCl 1M were added. Finally, it is poured with distilled water in 25mL volumetric flasks, and the pH values measured by passing the solutions to 25ml beakers. Absorption spectra are recorded against blanks prepared in the same manner, without reagent. The temperature was about 20±1°C.

Results and discussion

Though somewhat unpopular in the computer era, graphical analysis is a very appropriate method to study the acid-base behaviour of single equilibria from a spectrophotometric point of view. Since we may assume that in the pH range of choice there are only two species in solution, it is justifiable² to apply the methods already seen. The results obtained are shown in Table 6. Applying to these results the appropriate statistical criteria²⁴ we can admit that the average values of pK_a obtained from the classical expressions did not differ from those obtained with the new expressions. Moreover, there are also no significant differences as regards their precisions.

$λ (n m)$	Agren-Sommer Method		$Δ^{* *}$	Maroni-Calmon Method		$Δ^{* *}$	Nash Method
$λ (n m)$	Classic	Transformed	$Δ^{* *}$	Classic	Transformed	$Δ^{* *}$	Nash Method
340	10.903	10.926	0.023	10.961	10.965	0.004	10.951
345	10.909	10.931	0.022	10.963	10.967	0.004	10.939
*	10.906±0.004	10.928±0.003		10.962±0.001	10.966±0.001		10.945±0.008

Table 6 pKa₁ values at different wavelengths

(*) average value ±standard deviation

(**) $| p K_{a} c l a s s i c - p K_{a} t r a n s f o r m e d |$

However, some limitations are inherent to this study:

The calculations were only made for values of s_A=0.001 and s_pH=0.01.
It was assumed that absolute values of A are independent of the actual values for the whole range of absorbance found.
If the Gauss law holds for A and pH measurements, this is not necessary so for X and Y of the type used for the calculations in the manuscript; a serious objection, however, the authors does not know whether this is.
The variance analysis did not include the uncertainty of the instruments readings.

Transmittance and concentration are related by means of a logarithmic relationship, in such a way that small errors in transmittance measurement causing large relative absorbance errors. However, the main source of indeterminate error in modern spectrophotometers lies in the measure of the absorbance. However, the procedure devised in this paper has the inherent advantage of its simplicity, which makes it attractive. Bisthiosemicarbazones are clinically relevant for a variety of diseases, e.g. tuberculosis, viral infections, malaria and cancer.²⁵ Copper (II) uncharged lipophilic complexes of bisthiosemicarbazones posses fascinating biological activity^26–28including applications in nuclear medicine.²⁸ Recent reviews show the biological importance of thiosemicarbazones as anticancer agents.^25,29–33

Conclusion

Among the physico-chemical properties of molecules, the acidity constants are of vital importance both in the analysis of drugs as well as in the interpretation of their mechanism of action. The solution of many galenical problems requires the knowledge of the acidity constants of compounds having pharmaceutical interest. As it has previously indicated, calculation of acidity constants of monoprotic acids by graphical methods may be advantageously used in spite of the existence of modern black-box computer software’s. The exchange of the role of the variables X and Y of the classical Agren-Sommer and Maroni-Calmon methods resulted in new expressions that fulfil the mathematical conditions required for the regression analysis, and led to more simplified equations for the calculation of the pK_a and its individual standard deviation. As far as the results are concerned, there are no significant differences and, therefore, this reformulation may be considered valid. Note that bisthiosemicarbazones are biological relevant as shown at the end of the previous section.