In present communication, the Bianchi type-III, viscous string cosmological models have been investigated in scalar-tensor Brans-Dicke gravity. To obtain an exact solution of the Einstein field equations (EFE), it is assumed that the viscosity is the power function of energy density and the deceleration parameter (DP) as a function of cosmic time with suitable relation i.e. $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">[</mo>}sinh\mathrm{<mo\; stretchy="false">(</mo>}\alpha t{\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{1/n}$ , here $\alpha \mathrm{,}n\ne 0$ are constants. It is observed that the power index has the important significance on the evolution of string cosmological models. It is also noticed that the string tension density $\mathrm{<mo\; stretchy="false">(</mo>}\lambda \mathrm{<mo\; stretchy="false">)</mo>}$ is increasing function of time where as the energy density $\mathrm{<mo\; stretchy="false">(</mo>}\rho \mathrm{<mo\; stretchy="false">)</mo>}$  and the cosmological constant $\mathrm{<mo\; stretchy="false">(</mo>}\Lambda \mathrm{<mo\; stretchy="false">)</mo>}$  are decreasing with time and converges to a small value at late time. For better understanding of the model, we have also presented the kinematic and geometric properties of the models.

Keywords: brans-dicke gravity, cosmological constant, variable deceleration parameter

EFE, Einstein field equations; DP, deceleration parameter; GTR, general theory of relativity; BD, brans-dicke; DE, dark energy.

The early universe is well described by homogeneous and an isotropic cosmological model as it has only ordinary matter and gravity. Here the ordinary matter means, a matter with non negative pressure and ordinary gravity is based on the four-dimensional Einstein-Hilbert action. Recently observational data indicates that the discrepancy arises at late time, when the age of the universe is some billions years. In this context the Friedmann-Robertson- Walker model is a unique correspondence between the expansion rate and the distance scale. Although general theory of relativity (GTR) is the most suitable theory for describing universe as a whole, but still there are some physical phenomena which are to be addressed by GTR. For this purpose there is a need either to modify the theory or to introduce alternate theory which is suitable to address the universe in all aspects. During the investigations of research findings it have been noticed that many alternate/modified theories of gravity were proposed by cosmologists as and when required. Among all the available alternative theories, the scalar-tensor Brans-Dicke theory (BD)¹ of gravity is the most promising existing theory which has very effectively solves the problems of early time inflation and late time accelerating behaviour of the universe.² According to BD theory, the gravitational constantis not a constant but it varies with space and time. The Brans-Dicke gravity also relates the gravitation constant G  with scalar field $\varphi$  along with relation $\varphi \cong G^{-1}$ ). The action principle for the Brans-Dicke gravity is given as

$\mathcal{A}\mathrm{<mo>=</mo>}\frac{c^3}{16\pi }{\displaystyle {\int }_{\Re }}\mathrm{<mo\; stretchy="false">(</mo>}\varphi R+\omega {\varphi }^{-1}{\varphi }^{\nu }{\varphi }_{\nu }\mathrm{<mo\; stretchy="false">)</mo>}\sqrt{-g}{d}^{4}x+\Lambda \left(1\right)$

The variation of $\mathcal{A}$  for small changes of $g^{\mu \nu }$  leads to the field equations

$R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R\mathrm{<mo>=</mo>}-\frac{8\pi }{c_{\varphi }^4}{T}_{\mu \nu }-\frac{\omega }{{\varphi }^2}\left({\varphi }_{\mu }{\varphi }_{\nu }-\frac{1}{2}{g}_{\mu \nu }{\varphi }^{\delta }{\varphi }_{\delta }\right)-\frac{1}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}{\varphi }_{\mathrm{<mo>;</mo>}\mu \nu }-g_{\mu \nu }\square \varphi \mathrm{<mo\; stretchy="false">)</mo>}\left(2\right)$

where $R_{\mu \nu }$ is the Ricci curvature tensor, $T_{\mu \nu }$ is the energy momentum tensor, $R$ is the curvature scalar, $\omega$  is the Brans-Dicke dimensionless coupling constant, $T$ is the trace of energy momentum tensor andis wave operator. Also the law of conservation of momentum may be expressed as

$T_{\mathrm{<mo>;</mo>}k}^{\mu \nu }\mathrm{<mo>=</mo>0.}\left(3\right)$

Here ‘semicolon’ indicates co-variant derivative and ‘comma’ indicates partial derivatives.

Similarly, the variation of $\varphi$  leads to the following equation for $\varphi$ :

$2\varphi \square \varphi -{\varphi }_{\mu }{\varphi }^{\mu }\mathrm{<mo>=</mo>}\frac{R}{\omega }{\varphi }^2\mathrm{.}\left(4\right)$

This latter equation can be simplified by substituting for $R$  from the contracted form of Equation (2). We finally get

$\square \varphi \mathrm{<mo>=</mo>}\frac{8\pi }{\mathrm{<mo\; stretchy="false">(</mo>2}\omega +\mathrm{3<mo\; stretchy="false">)</mo>}{c}^4}T\mathrm{,}\left(5\right)$

Equation (5) leads to the anticipated scalar wave equation for $\varphi$ with sources in matter. Because it contains a scalar field $\varphi$ in addition to the metric tensor $g_{\mu \nu }$ , the BD theory is often referred to as the scalar-tensor theory of gravitation. BD theory is explained by a scalar function $\varphi$ and a constant coupling constant $\omega$ , often known as the BD parameter. This can be obtained from general theory of relativity by letting $\omega \to \infty$  and $\varphi \mathrm{<mo>=</mo>}constant$ .³

The recent cosmic observational results authenticate the fact that our universe is undergoing a late-time accelerated expansion phase.^4–8 To find the reason behind this late-time accelerating expansion of the universe is one of the most challenging problems in modern Cosmology and Astrophysics. We also believes that an unknown form of energy, commonly known as ’Dark Energy’ (DE), is responsible for this phase and it constitutes near about  of the total universe. There are several proposals regarding DE, Cosmological Constant, Quintessence, Dark Energy^9–14 being some of the competent candidates.

Viscosities play an important role in early stage evolution of the universe. Also it is well known that at early stage of the universe when neutrino decoupling occurred, the matter behaves like viscous fluid¹⁵ and coefficient of viscosity  decreases with time as universe expands. Recently viscous string cosmological models have been studied by several authors^16–26 in the context of general relativity, also many authors^27–32 had discussed bulk viscous string cosmological models in BD theory. Very recently^33–40 have been investigated the Bianchi type viscous cosmic string cosmological models in BD theory.

Motivated from above mention research work, in present paper, we had studied the bulk viscous string cosmological models with time dependentand cosmological constant  in scalar-tensor BD theory of gravity. This paper has been divided in five different sections, including the introduction presented in section 1. In section 2, the metric and field equations governing the cosmological models are described, section 3 deals with exact solution of field equations. Section 4, the physical and kinematic behavior of the models has been presented in both the cases. Finally results, discussion and conclusions are summarized in last section i.e. section 5.

In present communication, we consider a spatially homogeneous and an anisotropic Bianchi type-III space-time metric as given below

$d{s}^2\mathrm{<mo>=</mo>}-d{t}^2+A^2\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{x}^2+e^{-2sx}{B}^2\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{y}^2+C^2\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}d{z}^2\mathrm{,}\left(6\right)$

Here potential A, B and C are the functions of cosmic time $\text{'}t\text{'}$ only and $s$ is a constant.

The energy-momentum tensor $T_{\mu \nu }$ for a cloud of strings in the presence of bulk viscous fluid containing one dimensional cosmic string is given by

$T_{\mu \nu }\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}\rho +\overline{p}\mathrm{<mo\; stretchy="false">)</mo>}{u}_{\mu }{u}_{\nu }+\overline{p}{g}_{\mu \nu }-\lambda v_{\mu }{v}_{\nu }\mathrm{,}\left(7\right)$

$\lambda$ is the string tension density, $\overline{p}$ is effective pressure, $\rho$ is the proper energy density for cloud strings with particles attached to them, $u_k$ is the four-velocity vector and $x^k$ is a unit space-like vector along the direction of string. The vectors $u_k$ and $x^k$ satisfy the conditions $u_k{u}^k\mathrm{<mo>=</mo>1<mo>=</mo>}-x_k{x}^k$ , $u^k{x}_k\mathrm{<mo>=</mo>0}$ .

$T_{11}\mathrm{<mo>=</mo>}\overline{p}-\lambda \mathrm{,}{T}_{22}\mathrm{<mo>=</mo>}{T}_{33}\mathrm{<mo>=</mo>}\overline{p}\mathrm{,}{T}_{44}\mathrm{<mo>=</mo>}\rho \mathrm{,}$

$\Rightarrow T\mathrm{<mo>=</mo>}{T}_{11}+T_{22}+T_{33}+T_{44}\mathrm{<mo>=</mo>3}\overline{p}-\rho -\lambda \left(8\right)$

Above $\rho$ , $\overline{p}$  and $\lambda$  are the functions of cosmic time’t’ only. The particle density $\mathrm{<mo\; stretchy="false">(</mo>}{\rho }_p\mathrm{<mo\; stretchy="false">)</mo>}$  of the configuration is given as

$\rho \mathrm{<mo>=</mo>}{\rho }_p+\lambda \mathrm{,}\left(9\right)$

The string tension density $\lambda$ , may takes positive or negative values. It is also published by some authors^41,42 that a negative value of $\lambda$  represents the universe filled with no string, whereas positive value of $\lambda$  indicate the universe filled with string particles. Here the effective pressure $\overline{p}$  may be define as

$\overline{p}\mathrm{<mo>=</mo>}p-3\xi H\mathrm{,}\left(10\right)$

Where $\xi$  is the bulk viscosity coefficient and $H$  Hubble parameter.

For the metric given in equation (6) the field equation (2) may be expressed as:

$\frac{\ddot{A}}{A}+\frac{\ddot{B}}{B}+\frac{\dot{A}\dot{B}}{AB}-\frac{s^2}{A^2}+\frac{\ddot{\varphi }}{\varphi }+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{B}}{B}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\mathrm{<mo\; stretchy="false">(</mo>}\overline{p}-\lambda \mathrm{<mo\; stretchy="false">)</mo>}+\Lambda \mathrm{,}\left(11\right)$

$\frac{\ddot{C}}{C}+\frac{\ddot{A}}{A}+\frac{\dot{C}\dot{A}}{CA}+\frac{\ddot{\varphi }}{\varphi }+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\overline{p}+\Lambda \mathrm{,}\left(12\right)$

$\frac{\ddot{B}}{B}+\frac{\ddot{C}}{C}+\frac{\dot{B}\dot{C}}{BC}+\frac{\ddot{\varphi }}{\varphi }+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\overline{p}+\Lambda \mathrm{,}\left(13\right)$

$\frac{\dot{A}\dot{B}}{AB}+\frac{\dot{B}\dot{C}}{BC}+\frac{\dot{C}\dot{A}}{CA}-\frac{s^2}{A^2}-\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\rho +\Lambda \mathrm{,}\left(14\right)$

$\frac{\dot{A}}{A}-\frac{\dot{B}}{B}\mathrm{<mo>=</mo>0,}\left(15\right)$

$\ddot{\varphi }+\dot{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{B}}{B}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{8\pi \mathrm{<mo\; stretchy="false">(</mo>3}\overline{p}-\rho -\lambda \mathrm{<mo\; stretchy="false">)</mo>}}{\mathrm{<mo\; stretchy="false">(</mo>3}+2\omega \mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\left(16\right)$

Where an over head dot denote derivatives with respect to cosmic time $t$ .

We may introduce cosmological parameters such as the spatial volume $\mathrm{<mo\; stretchy="false">(</mo>}V\mathrm{<mo\; stretchy="false">)</mo>}$ , the Hubble’s parameter $\mathrm{<mo\; stretchy="false">(</mo>}H\mathrm{<mo\; stretchy="false">)</mo>}$ , the expansion scalar $\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}$ , the deceleration parameter $\mathrm{<mo\; stretchy="false">(</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}$ , the anisotropy parameter $\mathrm{<mo\; stretchy="false">(</mo>}{A}_m\mathrm{<mo\; stretchy="false">)</mo>}$ and the shear scalar $\mathrm{<mo\; stretchy="false">(</mo>}\sigma \mathrm{<mo\; stretchy="false">)</mo>}$  for the metric (6) connected as,

$V\mathrm{<mo>=</mo>}{a}^3\mathrm{<mo>=</mo>}ABC\mathrm{,}\left(17\right)$

$\theta \mathrm{<mo>=</mo>}{u}_{\mathrm{<mo>;</mo>}k}^k\mathrm{<mo>=</mo>3}H\mathrm{<mo>=</mo>}{H}_1+H_2+H_3\mathrm{,}\left(18\right)$

Here $H_1\mathrm{<mo>=</mo>}\frac{\dot{A}}{A}\mathrm{,}{H}_2\mathrm{<mo>=</mo>}\frac{\dot{B}}{B}\mathrm{,}{H}_3\mathrm{<mo>=</mo>}\frac{\dot{C}}{C}$ are the directional Hubble parameters in directions ofandaxis respectively.

$q\mathrm{<mo>=</mo>}-\frac{a\ddot{a}}{a^2}\mathrm{<mo>=</mo>}-\left(1+\frac{\dot{H}}{H^2}\right)\mathrm{.}\left(19\right)$

$A_m\mathrm{<mo>=</mo>}\frac{1}{3}{\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^3}{\left(\frac{\Delta H_i}{H}\right)}^2\mathrm{,}\left(20\right)$

${\sigma }^2\mathrm{<mo>=</mo>}\frac{1}{2}\left({\displaystyle \sum _{i\mathrm{<mo>=</mo>1}}^3}{H}_i^2-3H^2\right)\mathrm{,}\left(21\right)$

Here $\Delta H_i\mathrm{<mo>=</mo>}{H}_i-H\mathrm{,}i\mathrm{<mo>=</mo>1,2,3}$ .

Now we required the solution of above stated field equations 11-16. This is presented in next section.

On integrating equation (15), we have

$A\mathrm{<mo>=</mo>}{l}_{0}B\mathrm{,}\left(22\right)$

Here $l_0$ is a constant of integration it can be taken as unity to avoid further complication, therefore

$B\mathrm{<mo>=</mo>}A\mathrm{.}\left(23\right)$

Putting $‘t’$ into the field equations (11)-(14) and (16), we get following set of field equations,

$2\frac{\ddot{A}}{A}+\frac{{\dot{A}}^2}{A^2}-\frac{s^2}{A^2}+\frac{\ddot{\varphi }}{\varphi }+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+2\frac{\dot{A}}{A}\frac{\dot{\varphi }}{\varphi }\mathrm{<mo>=</mo>}-8\pi {\varphi }^{-1}\mathrm{<mo\; stretchy="false">(</mo>}\overline{p}-\lambda \mathrm{<mo\; stretchy="false">)</mo>}+\Lambda \mathrm{,}\left(24\right)$

$\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\dot{A}\dot{C}}{AC}+\frac{\ddot{\varphi }}{\varphi }+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\overline{p}+\Lambda \mathrm{,}\left(25\right)$

$\frac{{\dot{A}}^2}{A^2}+2\frac{\dot{A}\dot{C}}{AC}-\frac{s^2}{A^2}-\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>2}\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\rho +\Lambda \mathrm{,}\left(26\right)$

$\ddot{\varphi }+\dot{\varphi }\mathrm{<mo\; stretchy="false">(</mo>2}\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\frac{8\pi \mathrm{<mo\; stretchy="false">(</mo>3}\overline{p}-\rho -\lambda \mathrm{<mo\; stretchy="false">)</mo>}}{\mathrm{<mo\; stretchy="false">(</mo>3}+2\omega \mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{.}\left(27\right)$

The field equations 24-27 have a system of four independent equations along with seven unknown parameters $A\mathrm{,}C\mathrm{,}\lambda \mathrm{,}\rho \mathrm{,}\overline{p}\mathrm{,}\varphi$ and $\Lambda$ therefore we need at least three more constraints related to these parameters for explicit solution of this system of equations. For the explicit solution of above stated equations, we may apply following assumptions:

1. It is assumed that the bulk viscosity function $\xi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ is proportional to some power of energy density $\rho$  (see,^43,44i.e.

$\xi \propto {\rho }^{\beta }\mathrm{,}\left(28\right)$

$\xi \mathrm{<mo>=</mo>}{\xi }_0{\rho }^{\beta }\mathrm{,}\left(29\right)$

Here ${\xi }_0$  is proportional constant and $\beta \ge 0$  is a constant. Now with the help of equations (8), (25), (26) and (27) we get,

$\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{\varphi }}{\varphi }+\frac{\dot{A}\dot{C}}{AC}+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\mathrm{<mo\; stretchy="false">[</mo>}\gamma \rho -{\xi }_0{\rho }^{\beta }\theta \mathrm{<mo\; stretchy="false">]</mo>}+\Lambda \left(30\right)$

In this context we have discuss two cases i.e. $\beta \mathrm{<mo>=</mo>0}$  and $\beta \mathrm{<mo>=</mo>1.}$

1. Case 1: If $\beta \mathrm{<mo>=</mo>0}$ , then $\xi \mathrm{<mo>=</mo>}{\xi }_0$

$\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{\varphi }}{\varphi }+\frac{\dot{A}\dot{C}}{AC}+\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}\gamma \rho +\Lambda +8\pi {\xi }_0\theta {\varphi }^{-1}\left(31\right)$

On subtracting equation (26) from equation (31), we have

$\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{\varphi }}{\varphi }-\frac{\dot{A}\dot{C}}{AC}+\frac{\omega {\dot{\varphi }}^2}{{\varphi }^2}-\frac{\dot{A}\dot{\varphi }}{A\varphi }-{\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}\mathrm{<mo\; stretchy="false">)</mo>}}^2+\frac{s^2}{A^2}\mathrm{<mo>=</mo>8}\pi {\varphi }^{-1}\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}\rho +8\pi {\varphi }^{-1}{\xi }_0\theta \left(32\right)$

On substituting the value of $8\pi \rho {\varphi }^{-1}$  from equation (32) into equation (26), we have expression for cosmological constant $\Lambda$  as

$\Lambda \mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-8\pi {\varphi }^{-1}{\xi }_0\theta +\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{\varphi }}{\varphi }+\mathrm{<mo\; stretchy="false">(</mo>1}-2\gamma \mathrm{<mo\; stretchy="false">)</mo>}\frac{\dot{A}\dot{C}}{AC}+\mathrm{<mo\; stretchy="false">(</mo>1}+\gamma \mathrm{<mo\; stretchy="false">)</mo>}\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\mathrm{<mo\; stretchy="false">(</mo>1}-2\gamma \mathrm{<mo\; stretchy="false">)</mo>}\frac{\dot{A}\dot{\varphi }}{A\varphi }-\gamma \frac{{\dot{A}}^2}{A^2}+\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}\frac{\dot{C}\dot{\varphi }}{C\varphi }+\gamma \frac{s^2}{A^2}\left(33\right)$

2. Case 2: If $\beta \mathrm{<mo>=</mo>1}$ , then $\xi \mathrm{<mo>=</mo>}{\xi }_0\rho$

$8\pi \rho \mathrm{<mo>=</mo>}\frac{\varphi }{\mathrm{<mo\; stretchy="false">[</mo>}\gamma -1-{\xi }_0\theta \mathrm{<mo\; stretchy="false">]</mo>}}\mathrm{<mo\; stretchy="false">[</mo>}\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{\varphi }}{\varphi }-\frac{{\dot{A}}^2}{A^2}-\frac{\dot{A}C}{AC}+\frac{\omega {\dot{\varphi }}^2}{{\varphi }^2}-\frac{\dot{A}\dot{\varphi }}{A\varphi }+\frac{s^2}{A^2}\mathrm{<mo\; stretchy="false">]</mo>}\left(34\right)$

$\Lambda \mathrm{<mo>=</mo>}\frac{1}{\mathrm{<mo\; stretchy="false">[</mo>}\gamma -1-{\xi }_0\theta \mathrm{<mo\; stretchy="false">]</mo>}}\mathrm{<mo\; stretchy="false">[</mo>}\frac{\ddot{A}}{A}+\frac{\ddot{C}}{C}+\frac{\ddot{\varphi }}{\varphi }-\frac{{\dot{A}}^2}{A^2}-\frac{\dot{A}C}{AC}+\frac{\omega {\dot{\varphi }}^2}{{\varphi }^2}-\frac{\dot{A}\dot{\varphi }}{A\varphi }+\frac{s^2}{A^2}\mathrm{<mo\; stretchy="false">]</mo>}+{\mathrm{<mo\; stretchy="false">(</mo>}\frac{\dot{A}}{A}\mathrm{<mo\; stretchy="false">)</mo>}}^2+2\frac{\dot{A}\dot{C}}{AC}-\frac{s^2}{A^2}-\frac{\omega {\dot{\varphi }}^2}{2{\varphi }^2}+\frac{\dot{\varphi }}{\varphi }\mathrm{<mo\; stretchy="false">(</mo>}\frac{2\dot{A}}{A}+\frac{\dot{C}}{C}\mathrm{<mo\; stretchy="false">)</mo>}\left(35\right)$

2. The deceleration parameter $q$ is taken as a function of cosmic time $‘t’$ i.e.

$q\mathrm{<mo>=</mo>}-\frac{a\ddot{a}}{a^2}\mathrm{<mo>=</mo>}-\left(\frac{\dot{H}+H^2}{H^2}\right)\mathrm{<mo>=</mo>}b\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}say\mathrm{<mo\; stretchy="false">)</mo>}\left(36\right)$

As recent observations confirmed that the universe is expanding with an accelerating rate at present whereas it was decelerating at early time (see^4,5,8). Theoretically, we may say that the value of scale factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ vary with cosmic time. Also rate of expansion measured by Hubble’s parameter $\mathrm{<mo\; stretchy="false">(</mo>}H\mathrm{<mo\; stretchy="false">)</mo>}$ and the DP, $\mathrm{<mo\; stretchy="false">(</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}$ , since $H$  and $q$ are the functions of the scale factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ , therefore the study of various models with time dependent DP indicate new sector in theoretical Cosmology. Moreover, time-dependent $q$  dictates the expansion rate of the universe and also sign of the DP $q$ , galaxy number variation may be increasing (decelerated expansion), or decreasing (accelerated expansion).⁴⁵ Recent past several researchers including our research group³⁸ have been studied many cosmological models of the universe with time varying $q$ , in different context.^46–53

Now, the general solution of equation (36) is derived by our research team,³⁸ where we have defined $q\mathrm{<mo>=</mo>}b\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-a\ddot{a}/{\dot{a}}^2$ . The motivation to choose this type of DP is behind the fact that universe has an accelerating expanding phase at present time as observed by SNeIa supernova observations^4,8 and decelerated expansion in the past but in present scenario DP must show signature flipping,^5,54,55 so in general DP is not a constant but time variable so that above equation (36) may be re written as$a\ddot{a}/{\dot{a}}^2=0$ in order to solve above equation, we may assume $b\mathrm{<mo>=</mo>}b\mathrm{<mo\; stretchy="false">(</mo>}a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}$ as $a$ is also time dependent function, this only possible when we should avoid singularities like Big-Bang and Big-Rip because both the function (cosmic time & scale factor) are increasing functions therefore after some simplification we get,

$a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">(</mo>}\sinh \mathrm{<mo\; stretchy="false">(</mo>}\alpha t{\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>}}^{\frac{1}{n}}\mathrm{,}\left(37\right)$

Where $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ is a scale factor. Here $\alpha$ and $n$ are positive constants.

The shear scalar $\sigma$ is proportional to scalar expansion $\theta$ as suggested by,⁵⁶ we may also taken as

$A\mathrm{<mo>=</mo>}{C}^m\mathrm{,}\left(38\right)$

Here $m$ is non zero constant, which may takes care of the anisotropy of the space.

We consider the power law relation between scale factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ and BD scalar field $\varphi$ . As we know that the BD theory is a modification of Einstein’s GTR, where purely metric coupling of matter with gravity is preserved. Also the gravitational constant G is replaced with time dependent scalar field $\varphi$ as $\varphi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>18}\pi G$  and this scalar field couples to gravity with a BD coupling constant $\omega$ . It also passes the experimental tests from solar system⁵⁷ and able to provide a dynamicity of the universe.⁵⁸ In⁵⁹ had investigated Newtonian Cosmology with $G\propto a^{\beta }$ . There is another investigation of Cosmology i.e $\varphi \propto a^{\beta }$ .^60–62 Since the field equations (11)–(14) and (16) contain $a$ and $\varphi$ and their derivatives, so without any loss of generality, we shall assume that the BD scalar field $\varphi$ is some power of $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ . The power law relation between scale factor and scalar field has $\varphi$ already been used by⁶³ in the context of Robertson Walker Brans-Dicke models. Thus,

$\varphi \mathrm{<mo>=</mo>}{\varphi }_0{\mathrm{<mo\; stretchy="false">[</mo>}a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^b\mathrm{,}\left(39\right)$

Where ${\varphi }_0$  is a proportionality constant and $b$  is an ordinary constant. The assumption of a power law between the scalar field $\varphi$  and the cosmological expansion factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ , it is possible to reduce the cosmological equations to quadrature for the scalar-tensor theory with cosmological constant.^64–67 Now, from equations (17), (36) and (37), we have following expression for the metric potentials A, B and C,

$A\mathrm{<mo>=</mo>}B\mathrm{<mo>=</mo><mo\; stretchy="false">[</mo>}sinh\mathrm{<mo\; stretchy="false">(</mo>}\alpha t{\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{\frac{3m}{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}}\mathrm{,}\left(40\right)$

$C\mathrm{<mo>=</mo><mo\; stretchy="false">[</mo>}\sinh \mathrm{<mo\; stretchy="false">(</mo>}\alpha t{\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{\frac{3}{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}}\mathrm{,}\left(41\right)$

The directional Hubble parameters may be expressed as

$H_1\mathrm{<mo>=</mo>}{H}_2\mathrm{<mo>=</mo>}\frac{3m\alpha }{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}\coth \mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo>,}\left(42\right)$

$H_3\mathrm{<mo>=</mo>}\frac{3\alpha }{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}\coth \mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo>,}\left(43\right)$

The relation between scale factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$  and red shift parameter $z$  may be written as,

$1+z\equiv \frac{{\lambda }_{obs}}{{\lambda }_{emit}}\mathrm{<mo>=</mo>}\frac{a\mathrm{<mo\; stretchy="false">(</mo>}{t}_0\mathrm{<mo\; stretchy="false">)</mo>}}{a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\left(44\right)$

Where $a\mathrm{<mo\; stretchy="false">(</mo>}{t}_0\mathrm{<mo\; stretchy="false">)</mo>}$ is the present value of scale factor and it takes as unity. The scale factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ is stable under metric perturbation, so that redshift parameter in term of scale factor given as,

$a\mathrm{<mo>=</mo>}\frac{1}{1+z}\mathrm{,}\Rightarrow z\mathrm{<mo>=</mo>}-1+\frac{1}{a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}\mathrm{,}\Rightarrow z\mathrm{<mo>=</mo>}-1+{\mathrm{<mo\; stretchy="false">[</mo>}sinh\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{-\frac{1}{n}}\left(45\right)$

$z\mathrm{<mo>=</mo>}-1+{\mathrm{<mo\; stretchy="false">[</mo>}\alpha t+\frac{{\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo>}}^3}{\mathrm{3<mo>!</mo>}}+\frac{{\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo>}}^5}{\mathrm{5<mo>!</mo>}}+\mathrm{...<mo\; stretchy="false">]</mo>}}^{-\frac{1}{n}}$

The form of metric (4) after substituting the value of A,B and C,

$d{s}^2\mathrm{<mo>=</mo>}-d{t}^2+{\mathrm{<mo\; stretchy="false">[</mo>}sinh\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{\frac{6m}{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}}\mathrm{<mo\; stretchy="false">(</mo>}d{x}^2+e^{-2x}d{y}^2\mathrm{<mo\; stretchy="false">)</mo>}+{\mathrm{<mo\; stretchy="false">[</mo>}sinh\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{\frac{m}{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}}d{z}^2\left(46\right)$

Also we can write the metric (4) in terms of red shift parameter as Z as

$d{s}^2\mathrm{<mo>=</mo>}-d{t}^2+{\mathrm{<mo\; stretchy="false">[</mo>1}+z\mathrm{<mo\; stretchy="false">]</mo>}}^{\frac{-6m}{2m+1}}\mathrm{<mo\; stretchy="false">(</mo>}d{x}^2+e^{-2sx}d{y}^2\mathrm{<mo\; stretchy="false">)</mo>}+{\mathrm{<mo\; stretchy="false">[</mo>1}+z\mathrm{<mo\; stretchy="false">]</mo>}}^{\frac{-6}{2m+1}}d{z}^2\left(47\right)$

The some parameters such as spatial volume, Hubble parameter, deceleration parameter $\mathrm{<mo\; stretchy="false">(</mo>}q\mathrm{<mo\; stretchy="false">)</mo>}$ , expansion scalar $\mathrm{<mo\; stretchy="false">(</mo>}\theta \mathrm{<mo\; stretchy="false">)</mo>}$ , shear scalarand anisotropy parameter $A_m$ are expressed as

$V\mathrm{<mo>=</mo>}ABC\mathrm{<mo>=</mo><mo\; stretchy="false">[</mo>}\sinh \mathrm{<mo\; stretchy="false">(</mo>}\alpha t{\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^{\frac{3}{n}}\mathrm{,}\left(48\right)$

$\theta \mathrm{<mo>=</mo>3}H\mathrm{<mo>=</mo>}\frac{3\alpha }{n}\coth \mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo>,}\left(49\right)$

$q\mathrm{<mo>=</mo>}-1+n\mathrm{.}sec{h}^2\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo>,}\left(50\right)$

Also we have derived the relation between DPq and red shift Z for our considerable model 1, which is given by

$q\mathrm{<mo>=</mo>}-1+\frac{n{\mathrm{<mo\; stretchy="false">(</mo>1}+z\mathrm{<mo\; stretchy="false">)</mo>}}^{2n}}{1+{\mathrm{<mo\; stretchy="false">(</mo>1}+z\mathrm{<mo\; stretchy="false">)</mo>}}^{2n}}\mathrm{,}\left(51\right)$

If n=1, then

$q\mathrm{<mo>=</mo>}-\frac{1}{2}{\mathrm{<mo\; stretchy="false">[</mo>1}+\frac{z\mathrm{<mo\; stretchy="false">(</mo>}z+\mathrm{2<mo\; stretchy="false">)</mo>}}{2}\mathrm{<mo\; stretchy="false">]</mo>}}^{-1}provided\mathrm{<mo>|</mo>}\frac{z^2+2z}{2}\mathrm{<mo>|</mo><mo><</mo>1}\left(52\right)$

Also the Maclaurin’s series expansion of q is,

$q\mathrm{<mo>=</mo>}-\frac{1}{2}+\frac{1}{2}z-\frac{1}{2}{z}^2+O\mathrm{<mo\; stretchy="false">[</mo>}{z}^3\mathrm{<mo\; stretchy="false">]</mo>,}\left(53\right)$

For $n\mathrm{<mo>=</mo>}\frac{1}{2}$  

$q\mathrm{<mo>=</mo>}-\frac{1}{2}\mathrm{<mo\; stretchy="false">[</mo>}\frac{z+3}{z+2}\mathrm{<mo\; stretchy="false">]</mo>,}providedz\ne -2\left(54\right)$

For present age of the universe $t_0\mathrm{<mo>=</mo>13.78}Gyr$ with present value of DP $q_0\mathrm{<mo>=</mo>}-0.73$ ,⁶⁸ equation (50) yields the following relationship between the constants $\alpha$  and $n$ :

$\alpha \mathrm{<mo>=</mo>}\frac{1}{t_0}sec{h}^{-1}\sqrt{\frac{q_0+1}{n}}\left(55\right)$

From equation (50), we analyze that for q  is negative for $n\le 1$  and changing sing positive to negative for $n\mathrm{<mo>></mo>1}$  with corresponding value of $\alpha$ . In Figure 1, we depict the variation between red shift parameter $z$  with DP $q$ , the two most important parameters in cosmology. It is clear from concern that universe is accelerating for $n\le 1$  and show transition phase (i.e. early time deceleration to late time acceleration) for $n\mathrm{<mo>></mo>1}$ . This type behavior of DP $q$  indicates that the universe has decelerated in past and at present time undergoes an accelerating phase, which is good agreement with observational findings.

${\sigma }^2\mathrm{<mo>=</mo>}\frac{1}{3}{\mathrm{<mo\; stretchy="false">[</mo>}\frac{3\alpha \mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo>}}{n\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}coth\mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}}^2\mathrm{.}\left(56\right)$

$A_m\mathrm{<mo>=</mo>}\frac{2}{3}\mathrm{<mo\; stretchy="false">[</mo>}\frac{3m^2+2m+1}{{\mathrm{<mo\; stretchy="false">(</mo>2}m+\mathrm{1<mo\; stretchy="false">)</mo>}}^2}\mathrm{<mo\; stretchy="false">]</mo><mo>=</mo>}constant\mathrm{,}\left(57\right)$

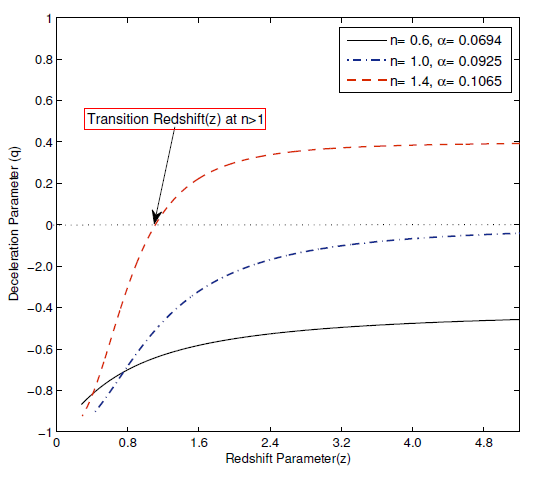
Figure 1 Plot of redshift parameter versus deceleration parameter q.

Provided $m\ne -\frac{1}{2}$

Above equation (57) indicates that $A_m$ is constant throughout evolution of the universe. This means universe never approaches to isotropy. Also, $\frac{\sigma }{\theta }\mathrm{<mo>=</mo>}constant$ this agreed with Collins et al. [54] results.

In this section we discuss the some physical and kinematic properties of the model represented by equation (46). The string tension density $\mathrm{<mo\; stretchy="false">(</mo>}\lambda \mathrm{<mo\; stretchy="false">)</mo>}$ , the energy density $\mathrm{<mo\; stretchy="false">(</mo>}\rho \mathrm{<mo\; stretchy="false">)</mo>}$ , the particle density $\mathrm{<mo\; stretchy="false">(</mo>}{\rho }_p\mathrm{<mo\; stretchy="false">)</mo>}$  and the cosmological constant $\mathrm{<mo\; stretchy="false">(</mo>}\Lambda \mathrm{<mo\; stretchy="false">)</mo>}$  for $\beta \mathrm{<mo>=</mo>0,1}$  may be expressed as

$8\pi \lambda \mathrm{<mo>=</mo>}\frac{{\varphi }_0{M}_2^{\frac{b}{n}}}{n^2{k}_1^2}\mathrm{<mo\; stretchy="false">[</mo>3}{\alpha }^2\mathrm{<mo>\{</mo>6}{m}^2-2m^{2}n-mn-3m+n-3+b{k}_1\mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo><mo>\}</mo>}{M}_1^2+3{\alpha }^{2}n{k}_1\mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo>}-s^2{n}^2{k}_1^2\mathrm{.}{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{<mo\; stretchy="false">]</mo>}\left(58\right)$

Here $M_1\mathrm{<mo>=</mo>}\coth \mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo><mo>;</mo>}$ ; $M_2\mathrm{<mo>=</mo>}\sinh \mathrm{<mo\; stretchy="false">(</mo>}\alpha t\mathrm{<mo\; stretchy="false">)</mo>}$ ; $k_1\mathrm{<mo>=</mo>2}m+1$ ; $l_1\mathrm{<mo>=</mo>}b{k}_1+b{k}_1\omega -6m$   $l_2\mathrm{<mo>=</mo>}{b}^2{k}_1+3m+\mathrm{3<mo>;</mo>}$   $l_3\mathrm{<mo>=</mo>3}{m}^2+b{k}_1+3.$

Case 1: $\beta \mathrm{<mo>=</mo>0}$              

$8\pi \rho \mathrm{<mo>=</mo>}\frac{{\varphi }_0{M}_2^{\frac{b}{n}}}{1-\gamma }\mathrm{<mo\; stretchy="false">[</mo>}\frac{{\alpha }^2\mathrm{<mo>\{</mo>}{k}_1\mathrm{<mo\; stretchy="false">(</mo>}b{l}_1-n{l}_2\mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{9<mo>\}</mo>}{M}_1^2}{n^2{k}_1^2}+s^2{M}_2^{\frac{-6m}{n{k}_1}}+\frac{{\alpha }^2{l}_3}{n{k}_1}\mathrm{<mo\; stretchy="false">]</mo>}-\frac{24\pi \alpha {\xi }_0{M}_1}{\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}n}\mathrm{,}\left(59\right)$

$\begin{array}{l}8\pi {\rho }_p\mathrm{<mo>=</mo>}\frac{{\varphi }_0{M}_2^{\frac{b}{n}}}{1-\gamma }\mathrm{<mo\; stretchy="false">[</mo>}\frac{{\alpha }^2\mathrm{<mo>\{</mo>}{k}_1\mathrm{<mo\; stretchy="false">(</mo>}b{l}_1-n{l}_2\mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{9<mo>\}</mo>}}{n^2{k}_1^2}\mathrm{.}{M}_1^2+\frac{{\alpha }^2\mathrm{<mo>\{</mo>3<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo><mo>\{</mo><mo\; stretchy="false">(</mo>}n-\mathrm{3<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>2}{m}^2-m-\mathrm{1<mo\; stretchy="false">)</mo>}+b{k}_1\mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo><mo>\}</mo><mo>\}</mo>}}{n^2{k}_1^2}{M}_1^2\\ +\frac{{\alpha }^2\mathrm{<mo>\{</mo>}{l}_3-\mathrm{3<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo><mo>\}</mo>}}{n{k}_1}+\mathrm{<mo\; stretchy="false">(</mo>2}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}{s}^2{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{<mo\; stretchy="false">]</mo>}-\frac{24\pi \alpha {\xi }_0{M}_1}{\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}n}\mathrm{,}\left(60\right)\end{array}$

$8\pi p\mathrm{<mo>=</mo>}\frac{\gamma M_2^{\frac{b}{n}}}{1-\gamma }\mathrm{<mo\; stretchy="false">[</mo>}\frac{{\alpha }^2\mathrm{<mo>\{</mo>}{k}_1\mathrm{<mo\; stretchy="false">(</mo>}b{l}_1-n{l}_2\mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{9<mo>\}</mo>}{M}_1^2}{n^2{k}_1^2}+s^2{M}_2^{\frac{-6m}{n{k}_1}}+\frac{{\alpha }^2{l}_3}{n{k}_1}\mathrm{<mo\; stretchy="false">]</mo>}-\frac{24\pi \alpha {\xi }_0\gamma M_1}{\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}n}\mathrm{,}\left(61\right)$

$\begin{array}{l}\mathrm{<mo\; stretchy="false">(</mo>}\gamma -\mathrm{1<mo\; stretchy="false">)</mo>}\Lambda \mathrm{<mo>=</mo>}\frac{24\pi {\xi }_0{M}_1{M}_2^{\frac{-b}{n}}}{n}-\frac{{\alpha }^2{M}_1^2}{n^2{k}_1^2}\mathrm{<mo>\{</mo>9}{m}^2-6m^{2}n-3n+9mn+9+b^2{k}_1^2\mathrm{<mo\; stretchy="false">(</mo>}b-n\mathrm{<mo\; stretchy="false">)</mo>}+9m-18\gamma m+\frac{\omega b^2{k}_1^2\mathrm{<mo\; stretchy="false">(</mo>1}+\gamma \mathrm{<mo\; stretchy="false">)</mo>}}{2}\\ -9\gamma m^2+3mb{k}_1\mathrm{<mo\; stretchy="false">(</mo>1}-2\gamma \mathrm{<mo\; stretchy="false">)</mo>}+3b{k}_1\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo><mo>\}</mo>}-\frac{{\alpha }^2\mathrm{<mo\; stretchy="false">(</mo>3}m+b{k}_1+\mathrm{3<mo\; stretchy="false">)</mo>}}{n{k}_1}-\gamma s^2{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{<mo\; stretchy="false">]</mo>}\left(62\right)\end{array}$

Case 2: $\beta \mathrm{<mo>=</mo>1}$  

$8\pi \rho \mathrm{<mo>=</mo>}\frac{n{\varphi }_0{M}_2^{\frac{b}{n}}}{\mathrm{<mo>\{</mo>}n\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}+3{\xi }_0{M}_1\mathrm{<mo>\}</mo>}}\mathrm{<mo\; stretchy="false">[</mo>}\frac{k_1\mathrm{<mo\; stretchy="false">(</mo>}b{l}_1-n{l}_2\mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{9<mo\; stretchy="false">)</mo>}}{n^2{k}_1^2}\mathrm{.}{M}_1^2+\frac{{\alpha }^2{l}_3}{n{k}_1}+s^2{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{<mo\; stretchy="false">]</mo>,}\left(63\right)$

$\begin{array}{l}8\pi {\rho }_p\mathrm{<mo>=</mo>}\frac{n{\varphi }_0{M}_2^{\frac{b}{n}}}{\mathrm{<mo>\{</mo>}n\mathrm{<mo\; stretchy="false">(</mo>1}-\gamma \mathrm{<mo\; stretchy="false">)</mo>}+3{\xi }_0{M}_1\mathrm{<mo>\}</mo>}}\mathrm{<mo\; stretchy="false">[</mo>}\frac{k_1\mathrm{<mo\; stretchy="false">(</mo>}b{l}_1-n{l}_2\mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{9<mo\; stretchy="false">)</mo>}}{n^2{k}_1^2}\mathrm{.}{M}_1^2+\frac{{\alpha }^2{l}_3}{n{k}_1}+s^2{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{<mo\; stretchy="false">]</mo>}-\frac{{\varphi }_0{M}_2^{\frac{b}{n}}}{n^2{k}_1^2}\mathrm{<mo\; stretchy="false">[</mo>3}{\alpha }^2\\ \mathrm{.<mo>\{</mo><mo\; stretchy="false">(</mo>}n-\mathrm{3<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>2}{m}^2-m-\mathrm{1<mo\; stretchy="false">)</mo>}+b{k}_1\mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo><mo>\}</mo>}{M}_1^2+3{\alpha }^{2}n{k}_1\mathrm{<mo\; stretchy="false">(</mo>}m-\mathrm{1<mo\; stretchy="false">)</mo>}-s^2{n}^2{k}_1^2\mathrm{.}{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{<mo\; stretchy="false">]</mo>,}\left(64\right)\end{array}$

$\Lambda \mathrm{<mo>=</mo>}\frac{n}{\mathrm{<mo>\{</mo>}n\mathrm{<mo\; stretchy="false">(</mo>}\gamma -\mathrm{1<mo\; stretchy="false">)</mo>}-3{\xi }_0{M}_1\mathrm{<mo>\}</mo>}}\mathrm{<mo\; stretchy="false">[</mo>}\frac{k_1\mathrm{<mo\; stretchy="false">(</mo>}b{l}_1-n{l}_2\mathrm{<mo\; stretchy="false">)</mo>}+\mathrm{9<mo\; stretchy="false">)</mo>}}{n^2{k}_1^2}\mathrm{.}{M}_1^2+s^2{M}_2^{\frac{-6m}{n{k}_1}}+\frac{{\alpha }^2{l}_3}{n{k}_1}\mathrm{<mo\; stretchy="false">]</mo>}+\frac{{\alpha }^2{M}_1^2}{n^2{k}_1^2}\mathrm{<mo\; stretchy="false">[</mo>}m\mathrm{<mo\; stretchy="false">(</mo>9}m+\mathrm{2<mo\; stretchy="false">)</mo>}-b{k}_1^2\mathrm{<mo\; stretchy="false">(</mo>}\omega b+\mathrm{6<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>}-s^2{M}_2^{\frac{-6m}{n{k}_1}}\mathrm{.}\left(65\right)$

From Figure 2, we observe that the string tension density $\lambda$ is an increasing function of time, which is always negative and approaches to zero at late time. As suggested by Letelier PS⁴¹ the string tension density $\lambda$ may have positive or negative values, corresponding to $\lambda \mathrm{<mo>></mo>0}$ the string dominant over particle where as in case of $\lambda \mathrm{<mo><</mo>0}$ the string disappear from universe. In our case the particles density dominate over the string tension density at present epoch. It is self exploratory from Figures 3 & 4 the energy density $\rho$ and particle density ${\rho }_p$ are decreasing function of cosmic time for both cases$\beta \mathrm{<mo>=</mo>0}$ and $\beta \mathrm{<mo>=</mo>1}$ .

Figure 2 Plot of string tension density $\lambda$ versus time t. For $b\mathrm{<mo>=</mo>}-1$ , $\omega \mathrm{<mo>=</mo>1}$ , ${\varphi }_0\mathrm{<mo>=</mo>1}$ .

Figure 3 Plot of energy density $\rho$ versus time $t$ . For $\beta \mathrm{<mo>=</mo>0,1}$ , $\omega \mathrm{<mo>=</mo>1}$ , $b\mathrm{<mo>=</mo>}-1$ , ${\varphi }_0\mathrm{<mo>=</mo>}{\xi }_0\mathrm{<mo>=</mo>1}$ .

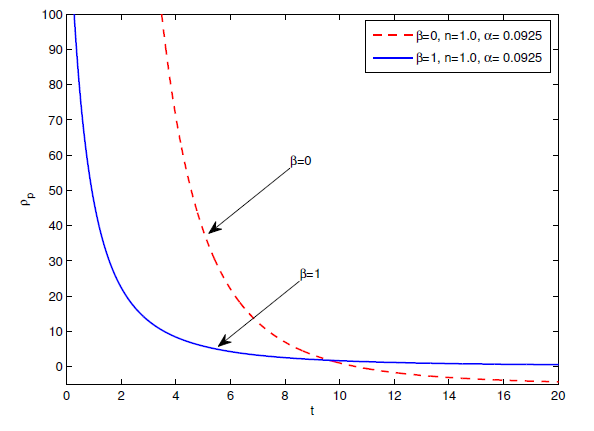
Figure 4 Plot of particle density ${\rho }_p$ versus time $t$ . For $\beta \mathrm{<mo>=</mo>0,1}$ , $\omega \mathrm{<mo>=</mo>1}$ , $b\mathrm{<mo>=</mo>}-1$ , ${\varphi }_0\mathrm{<mo>=</mo>}{\xi }_0\mathrm{<mo>=</mo>1}$ .

In Figure 5 we have plotted cosmological constant $\Lambda$ with cosmic time t. It may be seen from figure that cosmological constant $\Lambda$ is decreasing function of time and approaches to small value at late time. This type of behavior of $\Lambda$ is good agreement with recent cosmic observations.

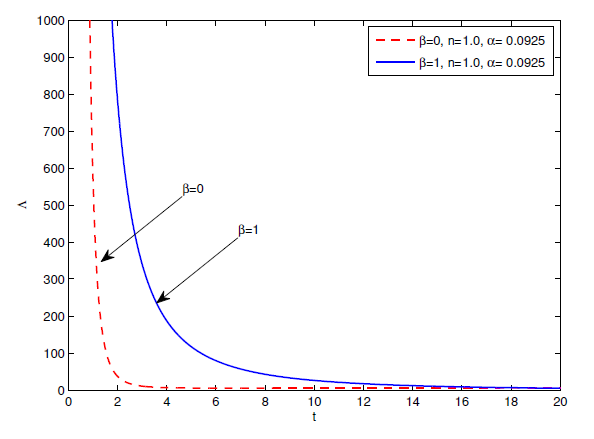
Figure 5 Plot of cosmological constant $\Lambda$ versus time $t$ . For $\beta \mathrm{<mo>=</mo>0,1}$ , $\omega \mathrm{<mo>=</mo>1}$ , $b\mathrm{<mo>=</mo>}-1$ , ${\varphi }_0\mathrm{<mo>=</mo>}{\xi }_0\mathrm{<mo>=</mo>1}$ .

We analyze from Figures 6 & 7 that the particle density is ${\rho }_p$ is always greater than string density for $\beta \mathrm{<mo>=</mo>0}$  and $\beta \mathrm{<mo>=</mo>1}$  at $n\mathrm{<mo>=</mo>1}$ , also the energy density decreasing with time.

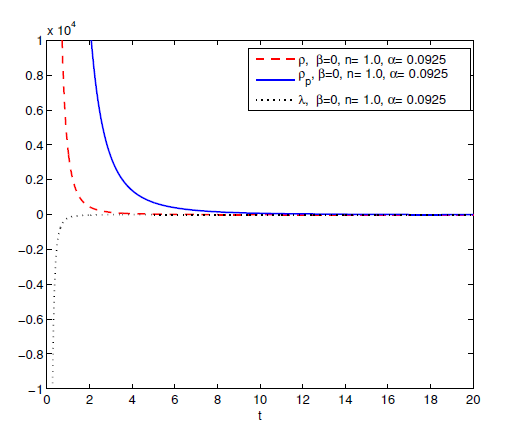
Figure 6 Plot of energy density $\rho$ , particle density ${\rho }_p$ and string tension density $\lambda$ versus time $t$ . For $\beta \mathrm{<mo>=</mo>0}$ , $\omega \mathrm{<mo>=</mo>1}$ , $b\mathrm{<mo>=</mo>}-1$ , ${\varphi }_0\mathrm{<mo>=</mo>}{\xi }_0\mathrm{<mo>=</mo>1}$ .

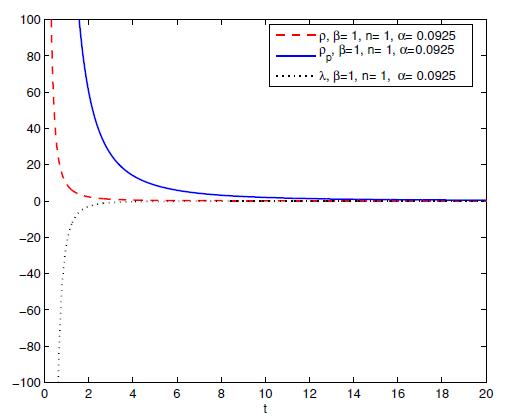
Figure 7 Plot of energy density $\rho$ , particle density ${\rho }_p$ and string tension density $\lambda$ versus time $t$ . For $\beta \mathrm{<mo>=</mo>1}$ , $\omega \mathrm{<mo>=</mo>1}$ , $b\mathrm{<mo>=</mo>}-1$ , ${\varphi }_0\mathrm{<mo>=</mo>}{\xi }_0\mathrm{<mo>=</mo>1}$ .

In Figure 8 we have presented the variation $\frac{{\rho }_p}{\mathrm{<mo>|</mo>}\lambda \mathrm{<mo>|</mo>}}$ with cosmic time t, the concern figure indicate that if $n\le 1$  then the particle density dominant over string tension density, but if $n\mathrm{<mo>></mo>1}$ then the string density dominant over particle density at early time (deceleration phase) but for acceleration phase the particle density greater than string density $\lambda$ .

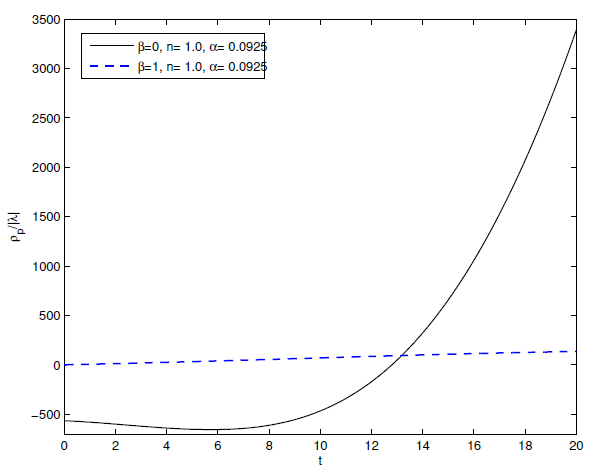
Figure 8 Plot of $\frac{{\rho }_p}{\mathrm{<mo>|</mo>}\lambda \mathrm{<mo>|</mo>}}$ versus time $t$ . For $\beta \mathrm{<mo>=</mo>0,1}$ , $\omega \mathrm{<mo>=</mo>1}$ , $b\mathrm{<mo>=</mo>}-1$ , ${\varphi }_0\mathrm{<mo>=</mo>}{\xi }_0\mathrm{<mo>=</mo>1}$ .

As discussed in this paper the Bianchi-III space-time viscous string cosmological models have been investigated in scalar-tensor BD theory of gravity with time dependent DPq and dynamical cosmological constant $\Lambda$ . The exact solution of EFE have been obtained by assuming viscosity as a some power function of energy density $\rho$ and the DPq  as a time function along with suitable assumptions on scale factor $a\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo><mo\; stretchy="false">[</mo>}sinh\mathrm{<mo\; stretchy="false">(</mo>}\alpha t){\mathrm{<mo\; stretchy="false">]</mo>}}^{\frac{1}{n}}$  , here $n$ and $\alpha$ are positive constants. We have presented a class of models with different choice $n$ of and $\beta$ . The main findings of the study are listed below:

• As discussed in section 3, (see equation 48)) the universe starts evolving from zero volume at $t\mathrm{<mo>=</mo>0}$ and thereafter expanding continuously from early decelerating phase to present accelerating phase. As, $t\to 0$ the expansion scalar $\theta \to \infty$ (see equation (49)), which indicates the early inflationary phase of the universe. Therefore we can say that the universe grow up from Big-Bang.
• It may also be pointed out that the universe was accelerating for $n\le 1$ and show transition phase i.e. early deceleration phase to current acceleration phase for.
• It is also observed form Figures 6 & 7 that for both the cases $\beta \mathrm{<mo>=</mo>0}$ and $\beta \mathrm{<mo>=</mo>1}$ , the string tension density $\lambda$ is negative whereas particle density $p_{\rho }$ is positive at early time. At late time both are converges to zero. Hence, the string disappears from universe.
• The cosmological constantis a decreasing function of time and it converges to a small positive value at late time (Figure 5). This type of behavior of cosmological constant $\Lambda$ is supported by recent observations data.

The author(s) are highly thankful to the referees for their constructive comments and suggestions to improve this manuscript.

Authors declare there is no conflict of interest.

1. Brans C, Dicke RH. Mach's Principle and a Relativistic Theory of Gravitation. Physical Review journal Archive. 1961;124(3).
2. Linde A. Extended chaotic inflation and spatial variations of the gravitational constant. Physics Letters B. 1990;238(2–4):160–165.
3. Sahoo BK, Singh LP. Cosmic Evolution in Generalised Brans-Dicke Theory. Modern Physics Letters A. 2003;18:1–12.
4. Riess RG, Filippenko AV, Challis P, et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. The Astronomical Journal. 1998;116(3):1009–1038.
5. Riess AG, Nugent PE, Gillil RL, et al. The Farthest Known Supernova: Support for an Accelerating Universe and a Glimpse of the Epoch of Deceleration. The Astrophysical Journal. 2001;560(1):49–71.
6. Riess AG, Strolger LG, Tonry J, et al. Type Ia Supernova Discoveries at z>1 From the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. The Astrophysical Journal. 2004;607(2):665–687.
7. Riess AG, Strolger LG, Casertano S, et al. New Hubble Space Telescope Discoveries of Type Ia Supernovae at z >1: Narrowing Constraints on the Early Behavior of Dark Energy. The Astrophysical Journal. 2007;659(1):98–121.
8. Perlmutter S, Aldering G, Goldhaber G, et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. The Astrophysical Journal. 1990;517(2):565–586.
9. Spergel DN, Verde L, Peiris HV, et al. First Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. The Astrophysical Journal Supplement Series. 2003;148(1):175–194.
10. Spergel S, Bean R, Doré O, et al. Wilkinson Microwave Anisotropy Probe (WMAP) Three Year Results: Implications for Cosmology. The Astrophysical Journal Supplement Series. 2007;170(2):377–408.
11. Caldwell RR, Dave R, Steinhardt PJ. Cosmological Imprint of an Energy Component with General Equation of State. Physical Review Letters. 1998;80(8):1582–1585.
12. Al-Rawaf AS, Taha MO. Cosmology of general relativity without energy-momentum conservation. General Relativity and Gravitation. 1996;28(8):935–952.
13. Sahni V, Starobinsky A. The Case for a Positive Cosmological Lambda-term. International Journal of Modern Physics D. 2000;9:373–444.
14. Padmanabhan T. Cosmological Constant-the Weight of the Vacuum. Physics Reports. 2003;380(5–6):235–320.
15. Klimek Z. Entropy per particle in the early Bianchi type-I Universe. Il Nuovo Cimento B. 1976;35(2):249–258.
16. Weinberg S. Entropy Generation and the Survival of Protogalaxies in an Expanding Universe. The Astrophysical Journal. 1971;168.
17. Novello M, Arauju RA. Qualitative analysis of homogeneous universes. Physical Review D. 1980;22(2).
18. Grøn Ø. Viscous inflationary universe models. Astrophysics and Space Science. 1990;173(2):191–225.
19. Berman MS. Cosmological models with variable gravitational and cosmological “constants”. General Relativity and Gravitation. 1991;23(4):465–469.
20. Pimentel LO. Exact self-creation cosmological solutions. Astrophysics and Space Science. 1985;116(2):395–399.
21. Barrow JD. String-driven inflationary and deflationary cosmological models. Nuclear Physics B. 1988;310(3–4):743–763.
22. Roy SR, Tiwari OP. Some inhomogeneous viscous fluid cosmological models of plane symmetry. Indian Journal of Pure and Applied Mathematics. 1983;14(2):233–243.
23. Pardhan A, Amirhashchi A, Jaiswal R. A new class of LRS Bianchi type-II dark energy models with variable EoS parameter. Astrophysics and Space Science. 2011;334(2):249–260.
24. Mohanty G, Pradhan BD. Cosmological mesonic viscous fluid model. International Journal of Theoretical Physics. 1998;31(1):151–160.
25. Singh JK, Ram S. Plane-symmetric mesonic viscous fluid cosmological model. Astrophysics and Space Science. 1996;236(2):277–284.
26. Singh JK. Viscous Modified Chaplygin Gas in Classical and Loop Quantum Cosmology. Nuovo Cimento. 2005;1208–1251.
27. Johri VB, Sudharsan R. BD-FRW Cosmology with Bulk Viscosity. Australian Journal of Physics. 1989;42(2):215–222.
28. Pimental LO. Exact solutions in Brans-Dicke theory with bulk viscosity. International Journal of Theoretical Physics. 1994;33(6):1335–1340.
29. Banerjee N, Beesham A. Brans-Dicke Cosmology with Causal Viscous Fluid. Australian Journal of Physics. 1996;49:899–903.
30. Wang XX. Bianchi Type-III String Cosmological Model with Bulk Viscosity in General Relativity. Chinese Physics Letters. 2005;22(1).
31. Bali R, Pradhan A. Bianchi type-III string cosmological models with time dependent bulk viscosity. Chinese Physics Letters. 2007;24(2):585–588.
32. Adhav KS, Nimkar AS, Dawande MV. N-dimensional string cosmological model in Brans–Dicke theory of gravitation. Astrophysics and Space Science. 2007;310(3–4):231–235.
33. Tiwari RK, Sharma S. Bianchi Type-I String Cosmological Model with Bulk Viscosity and Time-Dependent Λ term. Chinese Physics Letters. 2011;28(9).
34. Reddy DRK, Naidu RL, Naidu KD, et al. Kaluza-Klein universe with cosmic strings and bulk viscosity in f(R,T) gravity. Astrophysics and Space Science. 2013;346(1):261–265.
35. Reddy DRK, Naidu RL, Naidu KD, et al. LRS Bianchi type-II universe with cosmic strings and bulk viscosity in a modified theory of gravity. Astrophysics and Space Science. 2013;346(1):219–223.
36. Naidu RL, Reddy DRK, Ramprasad T, et al. Bianchi type-V bulk viscous string cosmological model in f(R,T) gravity. Astrophysics and Space Science. 2013;348(1):247–252.
37. Sagar TV, Rao CP, Vijaya RB, et al. Bianchi type-III bulk viscous string cosmological model in Brans-Dicke theory of gravitation. Astrophysics and Space Science. 2014;349(1):479–483.
38. Chawla C, Mishra RK, Pradhan A. String cosmological models from early deceleration to current acceleration phase with varying G and Λ. The European Physical Journal Plus. 2012;127.
39. Kiran M, Reddy DRK. Non-existence of Bianchi type-III bulk viscous string cosmological model in f(R,T) gravity. Astrophysics and Space Science. 2013;346(2):521–524.
40. Kiran M, Reddy DRK, Rao VUM. Bianchi type-III minimally interacting holographic dark energy model with linearly varying deceleration parameter in Brans-Dicke theory. Astrophysics and Space Science. 2015;360:54.
41. Letelier PS. String cosmologies. Physical Review D. 1983;28(10).
42. Berman MS, Som MM. Brans-Dicke models with time-dependent cosmological term. International Journal of Theoretical Physics. 1990;29(12):1411–1414.
43. Murphy GL. Big-Bang Model Without Singularities. Physical Review D. 1973;8(12).
44. Barrow JD. The deflationary universe: An instability of the de Sitter universe. Physics Letters B. 1987;180(4):335–339.
45. Bolotin YL, Cherkaskiy VA, Lemets OA, et al. Cosmology In Terms of the Deceleration Parameter. Part I. Cornell University Library, USA. 2015.
46. Mishra RK, Pradhan A, Chawla C. Anisotropic Viscous Fluid Cosmological Models from Deceleration to Acceleration in String Cosmology. International Journal of Theoretical Physics. 2013;52(8):2546–2559.
47. Mishra RK, Chand A, Pradhan A. Dark Energy Models in f(R, T) Theory with Variable Deceleration Parameter. International Journal of Theoretical Physics. 2016;55(2):1241–1256.
48. Mishra RK, Chand A, Pradhan A. FRW cosmological models in Brans-Dicke theory of gravity with variable q and dynamical Λ-term. Astrophysics and Space Science. 2016;361:81.
49. Mishra RK, Chand A. Cosmological models in alternative theory of gravity with bilinear deceleration parameter. Astrophysics and Space Science. 2016;361(8):259.
50. Mishra RK, Chand A. A comparative study of cosmological models in alternative theory of gravity with LVDP & BVDP. Astrophysics and Space Science. 2017;362(8).
51. Singh CP, Singh V. FRW models with perfect fluid and scalar field in higher derivative theory.Modern Physics Letters A. 2011;26(20):1495–1507.
52. Aguirregabiria JM, Chimento LP. Exact Bianchi type I models for an exponential-potential scalar field. Classical & Quantum Gravity. 1996;13(12).
53. El-Nabulsi RA. Asymptotically Static Universe Dominated by Phantom Energy. Zeitschrift für Naturforschung A. 2015;70(2):101–108.
54. Padmanabhan T, RoychowdhuryT. A theoretician's analysis of the supernova data and the limitations in determining the nature of dark energy. Monthly Notices of the Royal Astronomical Society. 2003;344(3):823–834.
55. Amendola L. Acceleration at z > 1? Monthly Notices of the Royal Astronomical Society. 2003;342(1):221–226.
56. Collins CB, Glass EN, Wilkinson DA. Exact spatially homogeneous cosmologies. General Relativity and Gravitation. 1980;12(10):805–823.
57. Bertotti B, Iess L, Tortora P. A test of general relativity using radio links with the Cassini spacecraft. Nature. 2003;425:374–376.
58. Mathiazhagan C, Johri VB. An inflationary universe in Brans-Dicke theory: a hopeful sign of theoretical estimation of the gravitational constant. Classical and Quantum Gravity. 1984;1(2).
59. Landsberg PT, Bishop NT. A Principle of Impotence Allowing for Newtonian Cosmologies with a time-Dependent Gravitational Constant. Monthly Notices of the Royal Astronomical Society. 1975;171(2):279–286.
60. Dehnen H, Obregon O. Exact cosmological solutions in Brans and Dicke's scalar-tensor theory, I. Astrophysics and Space Science. 1971;14(2):454–459.
61. Dehnen H, Obregon O. Exact cosmological solutions in Brans and Dicke's scalar-tensor theory, II. Astrophysics and Space Science. 1972;15(2):326–333.
62. Dehnen H, Obregon O. Cosmological vacuum solutions in Brans and Dicke's scalar-tensor theory. Astrophysics and Space Science. 1972;17(2):338–342.
63. Johri VB, Desikan K. Cosmological models with constant deceleration parameter in Brans-Dicke theory. General Relativity and Gravitation. 1994;26(12):1217–1232.
64. Pimentel LO. Exact cosmological solutions in the scalar-tensor theory with cosmological constant. Astrophysics and Space Science. 1985;112(1):175–183.
65. Gonzalez-Diaz PF, Ghosh DK, Moretti S. Diphoton signature of Higgs bosons in gauge mediated supersymmetry breaking models at the CERN LHC. Physical Review D. 2003;68(1).
66. Singh KM, Singh KP. String cosmological models in the Brans-Dicke theory for five-dimensional space-time. Research in Astronomy and Astrophysics. 2012;12(1).
67. Maurya D, Zia R, Pradhan A. Anisotropic string cosmological model in Brans-Dicke theory of gravitation with time-dependent deceleration parameter. Journal of Experimental and Theoretical Physics. 2016;150(4).
68. Cunha JV. Kinematic constraints to the transition redshift from supernovae type Ia union data. Physical Review D. 2009;79(4).