In this paper, compact effective potentials, charge distribution, Atomic Polar Tensor (APT) and Mulliken charges were studied using a unrestricted Hartree-Fock computational simulation in a protonated rhodochrosite crystal. The rhodochrosite crystal unit cell of structure CMn₆O₈, where the charge distribution by the molecule was verified in the UHF CEP-4G (Effective core potential (ECP) minimal basis), UHF CEP-31G (ECP split valance) and UHF CEP-121G (ECP triple-split basis). The largest load variation in the APT and Mulliken methods were obtained in the CEP-121G basis set, with δ=2.922 e δ=2.650 u.a., respectively, being δ_APT> δ_Mulliken. The maximum absorbance peaks in the CEP-4G, CEP-31G and CEP-121G basis set are present at the frequencies 2172.23 cm-¹, with a normalized intensity of 0.65; 2231.4 cm^-1 and 0.454; and 2177.24 cm^-1 and 1.0, respectively. An in-depth study is necessary to verify the absorption by the tumoral and non-tumoral tissues of rhodochrosite, before and after irradiating of synchrotron radiation using Small–Angle X–Ray Scattering (SAXS), Ultra–Small Angle X–Ray Scattering (USAXS), Fluctuation X–Ray Scattering (FXS), Wide–Angle X–Ray Scattering (WAXS), Grazing–Incidence Small–Angle X–Ray Scattering (GISAXS), Grazing–Incidence Wide–Angle X–Ray Scattering (GIWAXS), Small–Angle Neutron Scattering (SANS), Grazing–Incidence Small–Angle Neutron Scattering (GISANS), X–Ray Diffraction (XRD), Powder X–Ray Diffraction (PXRD), Wide–Angle X–Ray Diffraction (WAXD), Grazing– Incidence X–Ray Diffraction (GIXD) and Energy–Dispersive X–Ray Diffraction (EDXRD). Later studies could check the advantages and disadvantages of rhodochrosite in the treatment of cancer through synchrotron radiation, such as one oscillator crystal.

Keywords: rhodochrosite, quartz crystal, hartree-fock methods, apt, mulliken, effective core potential, synchrotron radiation, cancer, tumoral tissues

APT, atomic polar tensor; ECP, effective core potential; SAXS, small–angle X–ray scattering; USAXS, ultra–small angle X–ray scattering; FXS, X–ray scattering; WAXS, wide–angle X–ray scattering; GISAXS, grazing–incidence small–angle X–ray scattering; GIWAXS, grazing–incidence wide–angle X–ray scattering; SANS, small–angle neutron scattering; GISANS, grazing–incidence small–angle neutron scattering; XRD, X–ray diffraction; PXRD, powder X–ray diffraction; WAXD, wide–angle X–ray diffraction; GIXD grazing– incidence X–ray diffraction; EDXRD, energy–dispersive X–ray diffraction

The rhodochrosite as crystal oscillator for being an alternative to those of quartz. The rhodochrosite (MnC0₃) shows complete solid solution with siderite (FeC0₃), and it may contain substantial amounts of Zn, Mg, Co, and Ca. The electric charge that accumulates in certain solid materials, such as crystals, certain ceramics, and biological matter such as bone, DNA and various proteins in response to applied mechanical stress, phenomenon called piezoelectricity.¹ Through an unrestricted Hartree-Fock (UHF) computational simulation, Compact effective potentials (CEP), the infrared spectrum of the protonated rhodochrosite crystal, CH₁₉Mn₆O₈, and the load distribution by the unit molecule by two widely used methods, Atomic Polar Tensor (APT) and Mulliken, were studied. The rhodochrosite crystal unit cell of structure CMn₆O₈, where the load distribution by the molecule was verified in the UHF CEP-4G (Effective core potential (ECP) minimal basis), UHF CEP-31G (ECP split valance) and UHF CEP-121G (ECP triple-split basis).

The electronic oscillator circuit that uses the mechanical resonance of a vibrating crystal of piezoelectric material to create an electrical signal with a precise frequency is a crystal oscillator. The most common type of piezoelectric resonator used is the quartz crystal, so oscillator circuits incorporating them became known as crystal oscillators.² Quartz crystals are manufactured for frequencies from a few tens of kilohertz to hundreds of megahertz. More than two billion crystals are manufactured annually. Most are used for consumer devices such as wristwatches, clocks, radios, computers, cellphones, signal generators and oscilloscopes.^3–12 But other crystals such as rhodochrosite also have piezoelectric properties. The rhodochrosite as crystal oscillator for being an alternative to those of quartz. The rhodochrosite (MnC0₃) shows complete solid solution with siderite (FeC0₃), and it may contain substantial amounts of Zn, Mg, Co, and Ca. The Kutnohorite [CaMn(C0₃)₂] is a dolomite group mineral intermediary between rhodochrosite and calcite.^3–12 The Figure 1 is one photography the Rhodochrosite stone from China.

Figure 1 Rhodochrosite stone from China.¹³

Hartree-Fock methods

The Hartree-Fock self–consistent method^14–20 is based on the one-electron approximation in which the motion of each electron in the effective field of all the other electrons is governed by a one-particle Schrodinger¨ equation. The Hartree-Fock approximation takes into account of the correlation arising due to the electrons of the same spin, however, the motion of the electrons of the opposite spin remains uncorrelated in this approximation. The methods beyond self-consistent field methods, which treat the phenomenon associated with the many-electron system properly, are known as the electron correlation methods. The vast literature associated with these methods suggests that the following is a plausible hierarchy:

$HF << MP2 < CISD < CISD < CISD \left(T\right) < FCI$

The extremes of ‘best’, FCI, and ‘worst’, HF, are irrefutable, but the intermediate methods are less clear and depend on the type of chemical problem being addressed.¹⁴ The use of HF in the case of FCI was due to the computational cost. The molecular Hartree-Fock wave function is written as an antisymmetrized product (Slater determinant) of spin-orbitals, each spin-orbital being a product of a spatial orbital ${\varphi }_i$ and a spin function (either α or β). The expression for the Hartree-Fock molecular electronic energy $E_{HF }$ is given by the variation theorem as $E_{HF}=\langle D\left|{\widehat{H}}_{el}+V_{NN}\right|D\rangle$  where D is the Slater-determinant Hartree-Fock wave function and ${\widehat{H}}_{el}$ and $V_{NN}$ are given by

${\widehat{H}}_{\text{el}}= -\frac{{ħ}^2}{2m_e}{\displaystyle \sum }_i{\nabla }_i^2-{\displaystyle \sum }_{\alpha }{\displaystyle \sum }_i\frac{Z_{\alpha }e{\text{'}}^2}{r_{i\alpha }}+ {\displaystyle \sum }_j{\displaystyle \sum }_{i>j}\frac{e{\text{'}}^2}{r_{ij}}$

$V_{NN}= {\displaystyle \sum }_{\alpha }{\displaystyle \sum }_{\beta >\alpha }\frac{Z_{\alpha }{Z}_{\beta }e{\text{'}}^2}{r_{\alpha \beta }}$

Since $V_{NN}$ does not involve electronic coordinates and D is normalized, we have $\langle D\left|V_{NN}\right|D\rangle =V_{NN}\langle D|D\rangle =V_{NN}$ . The operator ${\widehat{H}}_{el}$ is the sum of one-electron operators ${\widehat{f}}_i$ and two-electron operators ${\widehat{g}}_{ij};$ we have ${\widehat{H}}_{el}= \underset{}{{\displaystyle {\displaystyle {\sum }_i{\widehat{f}}_i}+{\displaystyle {\sum }_j{\displaystyle {\sum }_{i>j}{\widehat{g}}_{ij}}}}}\text{ ,}$ where ${\widehat{f}}_i=-\frac{1}{2}{\nabla }_i^2{\sum }_{\alpha }{\sum }_{\alpha }/r_{ia}$  and ${\widehat{g}}_{ij}\text{=}\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r_{ij}$}\right..$ The Hamiltonian ${\widehat{H}}_{el}$ is the same as the Hamiltonian $\widehat{H}$  for an atom except that ${\sum }_{\alpha }{\sum }_{\alpha }/r_{ia}$ replaces $Z/r_i$ in ${\widehat{f}}_i\cdot$ Hence

$E=\langle D \text{|} \widehat{H} \text{|} D\rangle =2{\displaystyle \sum }_i^{n/2} \langle {\varphi }_i\left(1\right)\text{|}{\widehat{f}}_i\text{|}{\varphi }_i\left(2\right)\rangle +{\displaystyle \sum }_{j=1}^{n/2} {\displaystyle \sum }_{i=1}^{n/2} \left(2J_{ij}-K_{ij}\right)$

where

$J_{ij}= \langle {\varphi }_i\left(1\right){\varphi }_j\left(2\right)\text{|}e{\text{'}}^2/r_{12}\text{|}{\varphi }_i\left(1\right){\varphi }_j\left(2\right)\rangle$

And

$K_{ij}= \langle {\varphi }_i\left(1\right){\varphi }_j\left(2\right)\text{|}e{\text{'}}^2/r_{12}\text{|}{\varphi }_j\left(1\right){\varphi }_i\left(2\right)\rangle$

${\widehat{f}}_i= -\left({ħ}^2/2m_e\right){\nabla }_i^2- Ze{\text{'}}^2/r_1$

can be used to give $\langle D\text{|}{\widehat{H}}_{\text{el}}\text{|}D\rangle .$

Therefore, the Hartree-Fock energy of a diatomic or polyatomic molecule with only closed shells is

$E_{HF}= 2{\displaystyle \sum }_{i=1}^{n/2}{H}_i^{core} + {\displaystyle \sum }_{j=1}^{n/2}{\displaystyle \sum }_{i=1}^{n/2}\left(2J_{ij}-K_{ij}\right)+ V_{NN}$

$H_i^{core} \equiv \langle {\varphi }_i\left(1\right)\text{|}{\widehat{H}}^{core}\left(1\right)\text{|}{\varphi }_i\left(1\right)\rangle \equiv \langle {\varphi }_i\left(1\right)\text{|}-\frac{1}{2}{\nabla }_i^2 {\displaystyle \sum }_{\alpha }{Z}_{\alpha }/r_{1\alpha }\text{|}{\varphi }_i\left(1\right)\rangle$

$J_{ij}\equiv \langle {\varphi }_i\left(1\right){\varphi }_j\left(2\right)|1/r_{12}\text{|}{\varphi }_i\left(1\right){\varphi }_j\left(2\right)\rangle$

and

$K_{ij}\equiv \langle {\varphi }_i\left(1\right){\varphi }_j\left(2\right)\text{|}1/r_{12}\text{|}{\varphi }_j\left(1\right){\varphi }_i\left(2\right)\rangle$

where the one-electron-operator symbol was changed from ${\widehat{f}}_i$  to ${\widehat{H}}^{core}\left(1\right).$ ⁵

Mulliken load

Mulliken's loads are derived from the Mulliken population analysis and provide means for estimating partial atomic charges from numerical chemistry calculations, particularly those based on the linear combination of atomic orbitals. If the coefficients of the basic functions in the molecular orbital are C_μi for μ^e the basic function i^e in the orbital molecular, the coefficients of the density matrix are:

$D_{\mu \nu }=2\underset{i}{{\displaystyle \sum }}{C}_{\mu i}{C}_{\upsilon i}^{*}$

for a compact closed system in which each molecular orbital is doubly occupied. The population matrix P therefore has the following coefficients:

$P_{\mu \nu }={\left(DS\right)}_{\mu \nu }$

S is the overlay matrix for basic functions. The sum of the set of terms of $P_{\mu \nu }$ is N - the total number of electrons. The Mulliken population analysis aims first of all to distribute the N electrons on all the basic functions. This is done by taking the diagonal elements of $P_{\mu \nu }$ and factorizing the non-diagonal elements equally between the two appropriate basic functions. Non-diagonal terms including $P_{\mu \nu }$ and $P_{\nu \mu }$ this simplifies the operation to a sum on a line. This defines the gross orbital population (GOB) as:

$GO{P}_{\mu }= {\displaystyle \sum }_{\nu }{P}_{\mu \nu }$

The terms $GO{P}_{\mu }$ lie on N and then divide the total number of electrons between the basic functions. It then remains to sum these terms on all the basic functions of a given atom A in order to obtain the gross atomic population (GAP). The integral of the GAP_A terms also gives N. The load, Q_A, is then defined as the difference between the number of electrons on the free isolated atom, which is the atomic number Z_A, and the raw atomic population:

$Q_A= Z_A- GA{P}_A$

The problem with this approach is the even distribution of non-diagonal terms between the two basic functions. This leads to charge separations between the molecules that are exaggerated. Many other methods are used to determine atomic charges in molecules.^21,22 Concerning the nuclear contribution, the nuclear charge $Z_A$ can be written as $Z_A=q_A+Q_A,$  where $q_A$ and $Q_A$  account for the Mulliken net and gross atomic charge.²¹ According to the Mulliken population analysis, the nuclear charge for A can be written as

$Z_A= q_A+ {\displaystyle \sum }_{\mu } P_{\mu \mu }{S}_{\mu \mu }+ {\displaystyle \sum }_{\mu <\upsilon } 2P_{\mu \upsilon }{S}_{\mu \upsilon }+ \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\displaystyle \sum }_{B\ne A}\underset{\mu }{\overset{A}{{\displaystyle \sum }}}\underset{\nu }{\overset{B}{{\displaystyle \sum }}}2P_{\mu \upsilon }{S}_{\mu \upsilon }$

which upon substitution in the dipole moment expression yields

$\begin{array}{l}\langle {\widehat{p}}_x\rangle = -{\displaystyle \sum }_A{\displaystyle \sum }_{\mu }{P}_{\mu \mu }{X}_A- {\displaystyle \sum }_A{\displaystyle \sum }_{\mu <\nu }2P_{\mu \upsilon }{\varphi }_{\mu }\text{|}x\text{|}{\varphi }_{\upsilon }- {\displaystyle \sum }_{A<B}{\displaystyle \sum }_{\mu }^A{\displaystyle \sum }_{\nu }^{B}2P_{\mu \upsilon }{\varphi }_{\mu }\text{|}x\text{|}{\varphi }_{\upsilon }+ {\displaystyle \sum }_A{q}_A{X}_A\\ + {\displaystyle \sum }_A{\displaystyle \sum }_{\mu }{P}_{\mu \mu }{S}_{\mu \mu }{X}_A + {\displaystyle \sum }_A{\displaystyle \sum }_{\mu <\nu }2P_{{}_{\mu \nu }}{S}_{\mu \nu }{X}_A + \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\displaystyle \sum }_{A\ne B}{\displaystyle \sum }_{\mu }^A{\displaystyle \sum }_{\nu }^{B}2P_{\mu \upsilon }{S}_{\mu \upsilon }{X}_A\end{array}$

Note that $S_{\mu \upsilon }{X}_A= \langle {\varphi }_{\mu }\text{|}x\text{|}{\varphi }_{\upsilon }\rangle$ and $S_{\mu \upsilon }=1$ so that

$\langle {\widehat{p}}_x\rangle = + {\displaystyle \sum }_A{q}_A{X}_A- {\displaystyle \sum }_A{\displaystyle \sum }_{\mu <\nu }2P_{\mu \nu }{S}_{\mu \nu }{\overline{x}}_{\mu \nu }^A – {\displaystyle \sum }_{A<B}{\displaystyle \sum }_{\mu }^A{\displaystyle \sum }_{\nu }^{B}2P_{\mu \upsilon }{\overline{x}}_{\mu \nu }^{AB}$

where

${\overline{x}}_{\mu \nu }^A= \langle {\varphi }_{\mu }|x-X_A|{\varphi }_{\upsilon }\rangle$

and

${\overline{x}}_{\mu \nu }^{AB}= \langle {\varphi }_{\mu }\text{|}x- \frac{X_{A }+X_B}{2}\text{|}{\varphi }_{\upsilon }\rangle$

The first two terms in eq. for $\langle {\widehat{p}}_x\rangle$ are of atomic origin where the first one, involving the net atomic charge, is the only term with a classical counterpart. The second term resembles Coulson’s atomic dipole, and the integral ${\overline{x}}_{\mu \nu }^A$ is the distance from the centroid of the hybrid orbital to nucleus A. For the third term, the integral ${\overline{x}}_{\mu \nu }^{AB}=$ is the distance of the center of charge from the midpoint of the chemical bond A-B. This contribution to the dipole moment has been referred to as the homopolar dipole²¹ by Mulliken. As can be seen, the dipole moment has been partitioned into three contributions: the net atomic charge, the atomic dipole, and the homopolar dipole. Since the density matrix is invariant with respect to the choice of origin and since the sum of all net atomic charges vanishes, this partitioning of the dipole moment does not depend on the choice of origin for the system.^5,23

Atomic polar tensor (APT)

One of the most useful methods for interpreting and predicting infrared intensities comes from the atomic polar tensor (APT) formalism.^24,25 In the APT framework, the derivative of the molecular dipole moment vector with respect to the ith normal coordinate (which is directly related to the infrared intensity of the ith fundamental mode), can be expressed as

$\frac{\partial p}{\partial Q_i}= {\displaystyle \sum }_{\alpha }{\displaystyle \sum }_{\xi }\frac{\partial p}{\partial {\xi }_i}{\left[A{U}^{-1}L\right]}_{\xi \alpha ,i}$

For each atom α in molecule, the quantities $\raisebox{1ex}{$\partial p_{\tau }$}\!\left/ \!\raisebox{-1ex}{$\partial {\xi }_{\alpha }$}\right.= P_{\tau \xi }$ where $\tau =x, y, z$ and $\xi =X,Y,Z$ form the APT, represent by a $3\times 3$  matrix $p_x^{\left(\alpha \right)}$

$p_x^{\left(\alpha \right)}={\nabla }_{\alpha }p$

So, if all the experimental infrared intensities and normal coordinates are known as well as the permanent dipole moment for a given molecule, the APT can be determined. On the other hand, these APTs can also be calculated by the SCF method and used to predict infrared intensities. These intensities can then be interpreted by partitioning the APT. This has been done before in the "charge-charge flux-overlap" (CCFO) model, first introduced by King and Mast^26,27 and later applied by Person et al.²⁸

The general expression for the APT is:

${\nabla }_{\alpha }p= {\text{q}}_{\alpha }\text{E}+{\displaystyle \sum }_A\left({\nabla }_{\alpha }{\text{q}}_A\right)R_A-{\displaystyle \sum }_A{\displaystyle \sum }_{\mu <\upsilon }\nabla \left(2P_{\mu \upsilon }{\overline{R}}_{\mu \nu }^A\right) - {\displaystyle \sum }_{A<B}{\displaystyle \sum }_{\mu }^A{\displaystyle \sum }_{\nu }^{B}2P_{\mu \upsilon }{\overline{x}}_{\mu \nu }^{AB}$

where E is the identity matrix and each term of the APT is represented by a 3 X 3 matrix. The four contributions in the above equation can be identified according to Person, Coulson, and Mulliken terminology as charge, charge flux, atomic dipole flux, and homopolar dipole flux. Comparing with the CCFO model, the difference introduced in this work lies in the fact that the overlap term has been decomposed into two flux contributions (atomic dipole and homopolar dipole fluxes).

In eq. for ${\nabla }_{\alpha }p,$ the first two terms are the only classical contributions, one of them being the Mulliken net charge of atom a in its equilibrium position, $R_{\alpha },$ and the other being the "charge flux" corresponding to charge migration as the chemical bond involving the α atom has been distorted. The sum over all atoms, A, implies there is electronic density deformation involving all the atoms in the molecule. These two terms have already been well discussed by Person, Zilles, and other^28,29,30 The atomic dipole flux can be separated into two parts if the gradient of the density matrix and center of charge integrals are taken inside the parentheses:

$- {\displaystyle \sum _{\mu <\nu }^{\alpha }2P_{\mu \upsilon }}{\nabla }_{\text{α}}\left({\overline{R}}_{\mu \nu }^A\right)$

and

$- {\displaystyle \sum _A{\displaystyle \sum _{\mu <\nu }^{A}2}}\left(P_{\mu \upsilon }{\nabla }_{\text{α}}\right){\overline{R}}_{\mu \nu }^A$

the first of the two terms in equation

$- {\displaystyle \sum _A{\displaystyle \sum _{\mu <\nu }^{A}2}}\left(P_{\mu \upsilon }{\nabla }_{\text{α}}\right){\overline{R}}_{\mu \nu }^A$

 involves only the atom for which the APT is being calculated because only these $\varphi {\text{'}}_s$ depend on  $\left(r- R_{\alpha }\right).$

Hardware and software

For calculations a computer models was used: Intel^Ò Core^TM i3-3220 CPU @ 3.3 GHz x 4 processors,³¹ Memory DDR3 4 GB, HD SATA WDC WD7500 AZEK-00RKKA0 750.1 GB and DVD-RAM SATA GH24NS9 ATAPI, Graphics Intel^ Ivy Bridge.³² For calculations of computational dynamics, the Ubuntu Linux version 16.10 system was used³³ and the software used for the molecular dynamics was GAMESS.^16,34

The Figure 2 show on cell structure of a protonated rhodochrosite crystal of structure Stoichiometric is CH₁₉Mn₆O₈, obtained after molecular dynamics via unrestricted Hartree-Fock method, in basis set CEP-4G, CEP-31G and CEP-121G.^35–96 The Figure 3A–D) show the normalized absorption spectrum as a function of the vibrational frequencies of the protonated rhodochrosite crystal for UHF-CEP-4G basis set, UHF-CEP-31G and UHF-CEP-121G. The rhodochrosite crystal unit cell of structure CMn₆O₈, where the load distribution by the molecule was verified in the unrestricted Hartree-Fock method, UHF CEP-4G (Effective core potential (ECP) minimal basis), UHF CEP-31G (ECP split valance) and UHF CEP-121G (ECP triple-split basis), through the analysis of APT and Mulliken loads.^97–102 The rhodochrosite unit cell was protonated, then presented the structure CH₁₉Mn₆O₈ for the study with ab initio methods with +4 multiplicity. The displacement of charges by the molecule was analyzed to verify the site of molecular action. The load distribution by the protonated crystal is evaluated in Table 1, and its vibrational frequencies in Table 2. The Table 2 show the maximum absorbance peaks in the CEP-4G, CEP-31G and CEP-121G set basis are present at the frequencies 2172.23 cm^-1, with a normalized intensity of 65%; 2231.4 cm^-1 and 45.4%; and 2177.24 cm^-1 and 100%, respectively.

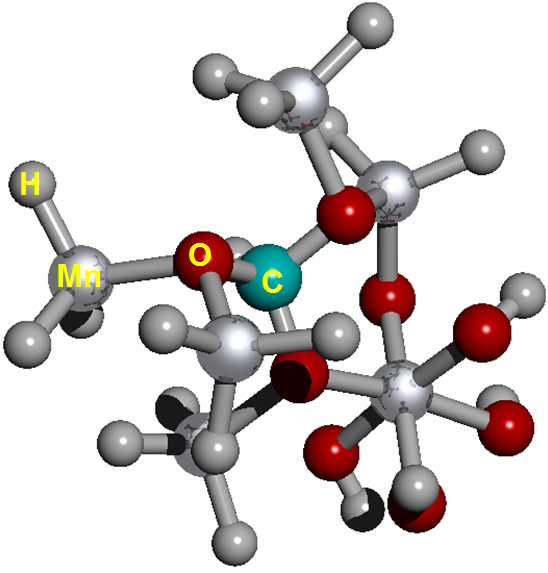
Figure 2 Cell structure of a protonated rhodochrosite crystal. Represented in red the oxygen; silver in color Manganese; in gray color Hydrogen; in light see green color the Carbon. Stoichiometry:   CMn₆O₈. Stoichiometry  protonated: CH₁₉Mn₆O₈.

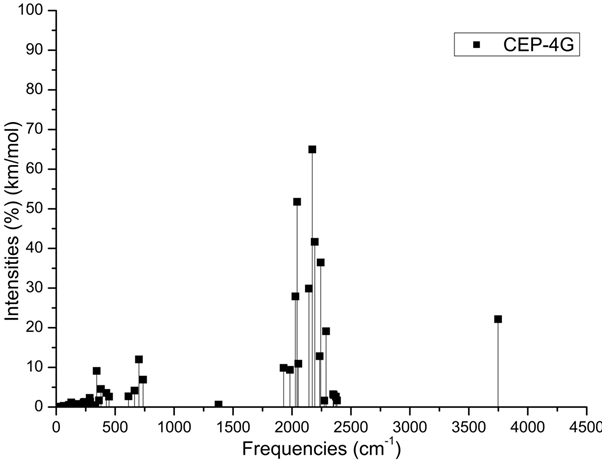
Figure 3A Absorbance spectrum plot as a function of vibrational frequencies of protonated rhodochrosite crystal for UHF-CEP-4G basis set.

Figure 3B Absorbance spectrum plot as a function of vibrational frequencies of protonated rhodochrosite crystal for UHF-CEP-31G basis set.

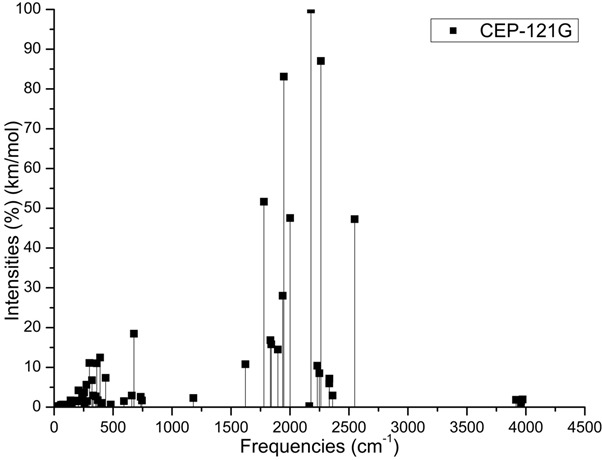
Figure 3C Absorbance spectrum plot as a function of vibrational frequencies of protonated rhodochrosite crystal for UHF-CEP-121G basis set.

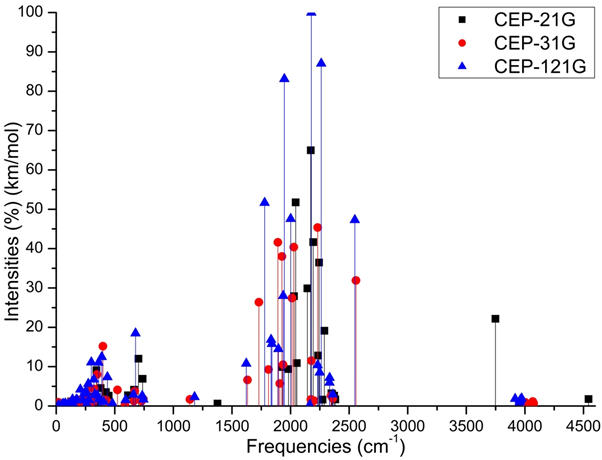
Figure 3D Absorbance spectrum plot as a function of vibrational frequencies of protonated rhodochrosite crystal for UHF-CEP-4G basis set, UHF-CEP-31G and UHF-CEP-121G.

Analysis

The Mulliken load method in the UHF-CEP-4G base set; UHF-CEP-31G and UHF-CEP-121G are sufficient to show that the sites of action of the rhodochrosite crystal structure are found in three Oxygen-linked Manganese atoms, which are attached to the central Carbon atom, as well as these. Oxygen atoms and the central Carbon. These Manganese atoms show a slight negative to neutral load shift in the CEP-4G set basis, neutral to positive in the CEP-31G and CEP-121G set basis at the Mulliken charges, (Figure 4). The charge displacement is strong in the oxygen atoms, especially those near the central carbon, with negative load in all set basis studied, both in the APT and Mulliken charges. The central carbon atom on all set basis is positively charged in both APT and Mulliken load, except Milliken in CEP-31G, which is neutral. As might be expected from the charges by APT, the strong positive load manganese atoms, the strong negative load oxygen, the positively charged carbon atom. The manganese atom farthest from the carbon atom has a slight positive to neutral load shift. The Mulliken load method presents a better result when compared to the APT, in the studied set basis, for protonated rhodochrosite crystal, with a smaller load variation δ=2,650 u.a for CEP-121G. The absorption peaks are in a Gaussian between the frequencies 1620 cm^-1 and 2520 cm^-1, Figure 3D. The largest load variation in the APT and Mulliken methods were obtained in the CEP-121G base set, with δ=2.922 e δ=2.650, respectively, being δ_APT > δ_Mulliken, in all sets of calculated basis, (Table 1).

Figure 4 UHF-CEP-4G; UHF-CEP-31G and UHF-CEP-121G for APT and Mulliken.

The absorption peaks are in a Gaussian between the frequencies 1620 cm^-1 and 2520 cm^-1. The Mulliken load method presents a better result when compared to the APT, in the studied set basis, for protonated rhodochrosite crystal, with a smaller load variation δ=2,650 u.a for CEP-121G. The maximum absorbance peaks in the CEP-4G, CEP-31G and CEP-121G set basis are present at the frequencies 2172.23 cm^-1, with a normalized intensity of 0.65, 2231.4 cm^-1 and 0.454 and 2177.24 cm^-1 and 1.0 respectively. Later studies could check the advantages and disadvantages of rhodochrosite in the treatment of cancer through synchrotron radiation, such as one oscillator crystal. An in-depth study is necessary to verify the absorption by the tumoral and non-tumoral tissues of rhodochrosite, before and after irradiating of synchrotron radiation using Small–Angle X–Ray Scattering (SAXS), Ultra–Small Angle X–Ray Scattering (USAXS), Fluctuation X–Ray Scattering (FXS), Wide–Angle X–Ray Scattering (WAXS), Grazing–Incidence Small–Angle X–Ray Scattering (GISAXS), Grazing–Incidence Wide–Angle X–Ray Scattering (GIWAXS), Small–Angle Neutron Scattering (SANS), Grazing–Incidence Small–Angle Neutron Scattering (GISANS), X–Ray Diffraction (XRD), Powder X–Ray Diffraction (PXRD), Wide–Angle X–Ray Diffraction (WAXD), Grazing– Incidence X–Ray Diffraction (GIXD) and Energy–Dispersive X–Ray Diffraction (EDXRD).

None.

The author declares there is no conflict of interest.

1. F James Holler, Douglas A. Skoog and Stanley R. Crouch. Principles of Instrumental Analysis. 6th ed. Cengage Learning. 200, p. 9.
2. Fox Electronics. Quartz Crystal Theory of Operation and Design Notes. Oscillator Theory of Operation and Design Notes. 2008.
3. RE Newnham. Properties of materials. Anisotropy, Simmetry, Structure. Oxford University Press, New York, 2005.
4. CD Gribble, AJ Hall. A Practical Introduction to Optical Mineralogy. 1985.
5. Creative Commons. (CC-BY 4.0). Wikipedia, The Free Encyclopedia. 2019.
6. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari. Rhodochrosite as Crystal Oscillator. Am J Biomed Sci & Res. 2019;3(2):AJBSR.MS.ID.000659.
7. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari. Calculation by UFF method of frequencies and vibrational temperatures of the unit cell of the rhodochrosite crystal. International Journal of Advanced Chemistry. 2019;7(2):77–81.
8. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari. Rhodochrosite as Crystal Oscillator. 2019. p. 1–2.
9. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari. Calculation by UFF method of frequencies and vibrational temperatures of the unit cell of the rhodochrosite crystal. International viXra.org Chemistry. viXra:1908.0294.
10. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari. Rhodochrosite as Crystal Oscillator. viXra.org, Condensed Matter, viXra:1908.0295.
11. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari, et al. Rhodochrosite Optical Indicatrix. Peer Res Nest. 2019;1(3):PNEST.19.08.020.
12. Ricardo Gobato, Marcia Regina Risso Gobato, Alireza Heidari, et al. Rhodochrosite Optical Indicatrix. Condensed Matter. 1908;0455.
13. China Science Communication. Baidu, 2019.
14. IN Levine. Quantum Chemistry. Pearson Education (Singapore) Pte. Ltd., Indian Branch, 48. In: FIE Patparganj editor. Delhi 110 092, India, 5th ed. edition, 2003.
15. A Szabo, NS Ostlund. Modern Quantum Chemistry. Dover Publications, New York, 1989. p. 1–479.
16. MS Gordon, Kim K Baldridge, Jerry A Boatz, et al. General atomic and molecular electronic structure system. J Comput Chem. 1993;14(11):1347–1363.
17. K Ohno, K Esfarjani, Y Kawazoe. Computational Material Science. Springer-Verlag, Berlin, 1999.
18. K Wolfram, MC Hothausen. Introduction to DFT for Chemists. John Wiley & Sons, Inc. New York, 2nd edn. 2001.
19. P Hohenberg, W Kohn. Inhomogeneous electron gas. Phys Rev. 1964;(136):B864–B871.
20. W Kohn, LJ Sham. Self-consistent equations including exchange and correlation effects. Phys Rev. 1965;140:A1133.
21. RS Mulliken. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I. J Chem Phys. 1955;23:1833–1840.
22. IG Csizmadia. Theory and Practice of MO Calculations on Organic Molecules. Elsevier, Amsterdam, 1976.
23. Ferreira MMC. Hartree-fock Methods Analysis Protonated Rhodochrosite Crystal and Potential in the Elimination of Cancer Cells Through Synchrotron Radiation. J Phys Chem. 1990;94:3220–3223.
24. Biarge JF, Herranz J, Morcillo J. Polarized basis sets and the calculation of infrared intensities from nuclear electric shielding tensors. An R Soc Esp Fis Quim Ser A. 1961;A57:81.
25. Person WB, Newton JH. Dipole moment derivatives and infrared intensities. I. Polar tensorsJ Chem Phys. 1974;61:1040.
26. King WT, Mast GB. Integrated intensities in hydrogen cyanide J Phys Chem. 1976;80:2521.
27. King WT. Vibrational Intensities in Infrared and Ramon Spectra: Person. In: WB Zerbi et al., editors. Elsevier: Amsterdam, 1982; Chapter 6.
28. Person WB, Zilles B, Rogers JD, et al.  Hartree-fock Methods Analysis Protonated Rhodochrosite Crystal and Potential in the Elimination of Cancer Cells Through Synchrotron Radiation. RGAJ Mol Struct. 1982;80:297.
29. Zilles BA. Ph.D. Dissertation, University of Florida, 1980.
30. Zilles BA, Person W. Interpretation of infrared intensity changes on molecular complex formation. I. Water dimer. J Chem Phys. 1983;79:65.
31. Creative Commons, (CC BY 4.0), “List of Intel Core i3 microprocessors. 2018.
32. “Ivy Bridge”. 2018.
33. Ubuntu (operating system). 2018.
34. MS Gordon, MW Schmidt. Advances in electronic structure theory: GAMESS a decade later. Theory and Applications of Computational Chemistry: the first forty years. Elsevier. In: CE Dykstra et al., editors. 2005. p. 1167–1189.
35. R Gobato, A Gobato, DFG Fedrigo. Inorganic arrangement crystal beryllium, lithium, selenium and silicon. In XIX Semana da Física. Simpósio Comemorativo dos 40 anos do Curso de Física da Universidade Estadual de Londrina, Brazil, 2014. Universidade Estadual de Londrina (UEL). 2014.
36. R Gobato. Benzocaína, um estudo computacional”, Master’s thesis, Universidade Estadual de Londrina (UEL), 2008.
37. R Gobato. Study of the molecular geometry of Caramboxin toxin found in star flower (Averrhoa carambola L.). Parana J Sci Edu. 2017;3(1):1–9.
38. R Gobato, A Gobato, DFG Fedrigo. Molecular electrostatic potential of the main monoterpenoids compounds found in oil Lemon Tahiti - (Citrus Latifolia Var Tahiti). Parana J Sci Edu. 2015;1(1):1–10.
39. R Gobato, DFG Fedrigo, A Gobato. Allocryptopine, Berberine, Chelerythrine, Copsitine, Dihydrosanguinarine, Protopine and Sanguinarine. Molecular geometry of the main alkaloids found in the seeds of Argemone Mexicana Linn. Parana J Sci Edu. 2015;1(2):7–16.
40. R Gobato, A Heidari. Infrared Spectrum and Sites of Action of Sanguinarine by Molecular Mechanics and ab initio Methods. International Journal of Atmospheric and Oceanic Sciences. 2018;2(1):1–9.
41. R Gobato, DFG Fedrigo, A Gobato. Molecular geometry of alkaloids present in seeds of mexican prickly poppy. Cornell University Library. 2015;arXiv:1507.05042.
42. R Gobato, A Gobato, DFG Fedrigo. Study of the molecular electrostatic potential of D-Pinitol an active hypoglycemic principle found in Spring flower Three Marys (Bougainvillea species) in the Mm+ method. Parana J Sci Educ. 2016;2(4):1–9.
43. R Gobato, DFG Fedrigo, A Gobato. Avro: key component of Lockheed X-35. Parana J Sci Educ. 2015;1(2):1–6.
44. R Gobato, DFG Fedrigo, A Gobato. LOT-G3: Plasma Lamp, Ozonator and CW Transmitter. Ciencia e Natura. 2016;38(1).
45. R Gobato. Matter and energy in a non-relativistic approach amongst the mustard seed and the faith. A metaphysical conclusion. Parana J Sci Educ. 2016;2(3):1–14.
46. R Gobato, A Gobato, DFG Fedrigo. Harnessing the energy of ocean surface waves by Pelamis System. Parana J Sci Educ. 2016;2(2):1–15.
47. R Gobato, A Gobato, DFG Fedrigo. Mathematics for input space probes in the atmosphere of Gliese 581d. Parana J Sc. Educ. 2016;2(5):6–13.
48. R Gobato, A Gobato, DFG Fedrigo. Study of tornadoes that have reached the state of Parana. Parana J Sci Educ. 2016;2(1):1–27.
49. R Gobato, M Simões F. Alternative Method of RGB Channel Spectroscopy Using a CCD Reader. Ciencia e Natura. 2017;39(2):1–9.
50. R Gobato, A Heidari. Calculations Using Quantum Chemistry for Inorganic Molecule Simulation BeLi2SeSi. Science Journal of Analytical Chemistry. 2017;5(5):76–85.
51. R Gobato. O universo dos cristais líquidos”, Cadernos PDE, Secretaria de Estado da Educação do Paraná. 2009; 2:1–15
52. R Gobato. The Liotropic Indicatrix. Thesis (Doctorate in Pysics). Universidade Estadual de Londrina, Londrina, 2012. p. 114.
53. R Gobato, A Heidari. Calculations Using Quantum Chemistry for Inorganic Molecule Simulation BeLi2SeSi. Science Journal of Analytical Chemistry. 2017;5(6):76–85.
54. MRR Gobato, R Gobato, A Heidari. Planting of Jaboticaba Trees for Landscape Repair of Degraded Area. Landscape Architecture and Regional Planning. 2018;3(1):1–9.
55. R Gobato, A Heidari. Molecular Mechanics and Quantum Chemical Study on Sites of Action of Sanguinarine Using Vibrational Spectroscopy Based on Molecular Mechanics and Quantum Chemical Calculations. Malaysian Journal of Chemistry. 2018;20(1):1–23.
56. A Heidari, R Gobato. A Novel Approach to Reduce Toxicities and to Improve Bioavailabilities of DNA/RNA of Human Cancer Cells–Containing Cocaine (Coke), Lysergide (Lysergic Acid Diethyl Amide or LSD), Δ⁹–Tetrahydrocannabinol (THC) [(–)–trans–Δ⁹–Tetrahydrocannabinol], Theobromine (Xantheose), Caffeine, Aspartame (APM) (NutraSweet) and Zidovudine (ZDV) [Azidothymidine (AZT)] as Anti–Cancer Nano Drugs by Coassembly of Dual Anti–Cancer Nano Drugs to Inhibit DNA/RNA of Human Cancer Cells Drug Resistance. Parana Journal of Science and Education. 2018;4(6):1–17.
57. A Heidari, R Gobato. Ultraviolet Photoelectron Spectroscopy (UPS) and Ultraviolet–Visible (UV–Vis) Spectroscopy Comparative Study on Malignant and Benign Human Cancer Cells and Tissues with the Passage of Time under Synchrotron Radiation. Parana Journal of Science and Education. 2018; 4(6):8–33.
58. R Gobato, A Heidari. Using the Quantum Chemistry for Genesis of a Nano Biomembrane with a Combination of the Elements Be, Li, Se, Si, C and H. J Nanomed Res. 2018;7(4):241–252.
59. SK Agarwal, S Roy, P Pramanick, et al. Marsilea quadrifolia: A floral species with unique medicinal properties.  Parana J Sci Educ. 2018;4(5):15–20.
60. A Mitra, S Zaman, R Gobato. Indian Sundarban Mangroves: A potential Carbon Scrubbing System. Parana J Sci Educ. 2018;4(4):7–29.
61. O Yarman, R Gobato, T Yarman. A new Physical constant from the ratio of the reciprocal of the “Rydberg constant” to the Planck length. Parana J Sci Educ. 2018;4(3):42–51.
62. R Gobato, M Simões F. Alternative Method of Spectroscopy of Alkali Metal RGB. Modern Chemistry. 2017;5(4):70–74.
63. DFG Fedrigo, R Gobato, A Gobato. Avrocar: a real flying saucer”, Cornell University Library. 2015;arXiv:1507.06916v1.
64. M Simões F, AJ Palangana, R Gobato, et al. Micellar shape anisotropy and optical indicatrix in reentrant isotropic-nematic phase transitions. The Journal of Chemical Physics. 2012;137:204905.
65. A Heidari, R Gobato. Putrescine, Cadaverine, Spermine and Spermidine–Enhanced Precatalyst Preparation Stabilization and Initiation (EPPSI) Nano Molecules. Parana Journal of Science and Education (PJSE). 2018;4(5):1–14.
66. R Gobato, A Heidari. Molecular Mechanics and Quantum Chemical Study on Sites of Action of Sanguinarine Using Vibrational Spectroscopy Based on Molecular Mechanics and Quantum Chemical Calculations. Malaysian Journal of Chemistry. 2018;20(1):1–23.
67. R Gobato, A Heidari, A Mitra. The Creation of C13H20BeLi2SeSi. The Proposal of a Bio–Inorganic Molecule, Using Ab Initio Methods for the Genesis of a Nano Membrane. Arc Org Inorg Chem Sci. 2018;3(4):AOICS.MS.ID.000167.
68. R Gobato, A Heidari, A Mitra. Using the Quantum Chemistry for Genesis of a Nano Biomembrane with a Combination of the Elements Be, Li, Se, Si, C and H. Semantic Scholar. 2018.
69. A Heidari, R Gobato. First–Time Simulation of Deoxyuridine Monophosphate (dUMP) (Deoxyuridylic Acid or Deoxyuridylate) and Vomitoxin (Deoxynivalenol (DON)) ((3α,7α)–3,7,15–Trihydroxy–12,13–Epoxytrichothec–9–En–8–One)–Enhanced Precatalyst Preparation Stabilization and Initiation (EPPSI) Nano Molecules Incorporation into the Nano Polymeric Matrix (NPM) by Immersion of the Nano Polymeric Modified Electrode (NPME) as Molecular Enzymes and Drug Targets for Human Cancer Cells, Tissues and Tumors Treatment under Synchrotron and Synchrocyclotron Radiations. Parana Journal of Science and Education. 2018;4(6):46–67.
70. R Gobato, MRR Gobato, A Heidari, et al. Spectroscopy and Dipole Moment of the Molecule C13H20BeLi2SeSi via Quantum Chemistry Using Ab Initio, Hartree–Fock Method in the Base Set CC–pVTZ and 6–311G**(3df, 3pd). Arc Org Inorg Chem Sci. 2018;3(5):402–409.
71. R Gobato, MRR Gobato, A Heidari, et al. Spectroscopy and Dipole Moment of the Molecule C13H20BeLi2SeSi via Quantum Chemistry Using Ab Initio, Hartree–Fock Method in the Base Set CC–pVTZ and 6–311G**(3df, 3pd). American Journal of Quantum Chemistry and Molecular Spectroscopy. 2018;2(1):9–17.
72. R Gobato, MRR Gobato, A Heidari. Raman Spectroscopy Study of the Nano Molecule C13H20BeLi2SeSi Using ab initio and Hartree–Fock Methods in the Basis Set CC–pVTZ and 6–311G** (3df, 3pd). International Journal of Advanced Engineering and Science. 2019;7(1):14–35.
73. A Heidari, R Gobato. Evaluating the Effect of Anti–Cancer Nano Drugs Dosage and Reduced Leukemia and Polycythemia Vera Levels on Trend of the Human Blood and Bone Marrow Cancers under Synchrotron Radiation. Trends in Res. 2019;2(1):1–8.
74. A Heidari, R Gobato. Assessing the Variety of Synchrotron, Synchrocyclotron and LASER Radiations and Their Roles and Applications in Human Cancer Cells, Tissues and Tumors Diagnosis and Treatment. Trends in Res. 2019;2(1):1–8.
75. A Heidari, R Gobato. Pros and Cons Controversy on Malignant Human Cancer Cells, Tissues and Tumors Transformation Process to Benign Human Cancer Cells, Tissues and Tumors. Trends in Res. 2019;2(1):1–8.
76. A Heidari, R Gobato. Three–Dimensional (3D) Simulations of Human Cancer Cells, Tissues and Tumors for Using in Human Cancer Cells, Tissues and Tumors Diagnosis and Treatment as a Powerful Tool in Human Cancer Cells, Tissues and Tumors Research and Anti–Cancer Nano Drugs Sensitivity and Delivery Area Discovery and Evaluation. Trends in Res. 2019;2(1):1–8.
77. A Heidari, R.Gobato. Investigation of Energy Production by Synchrotron, Synchrocyclotron and LASER Radiations in Human Cancer Cells, Tissues and Tumors and Evaluation of Their Effective on Human Cancer Cells, Tissues and Tumors Treatment Trend. Trends in Res. 2019;2(1):1–8.
78. A Heidari, R. Gobato. High–Resolution Mapping of DNA/RNA Hypermethylation and Hypomethylation Process in Human Cancer Cells, Tissues and Tumors under Synchrotron Radiation. Trends in Res. 2019;2(2):1–9.
79. R Gobato, MRR Gobato, A Heidari. Storm Vortex in the Center of Paraná State on June 6, 2017: A Case Study. Sumerianz Journal of Scientific Research. 2019;2(2):24–31.
80. R Gobato, MRR Gobato, A Heidari. Attenuated Total Reflection–Fourier Transform Infrared (ATR–FTIR) Spectroscopy Study of the Nano Molecule C13H20BeLi2SeSi Using ab initio and Hartree–Fock Methods in the Basis Set RHF/CC– pVTZ and RHF/6–311G** (3df, 3pd): An Experimental Challenge to Chemists. Chemistry Reports. 2019;2(1):1–26.
81. R Gobato, MRR Gobato, A Heidari, et al. New Nano–Molecule Kurumi–C13H 20BeLi2SeSi/C13H19BeLi2SeSi, and Raman Spectroscopy Using ab initio, Hartree–Fock Method in the Base Set CC–pVTZ and 6–311G** (3df, 3pd). J Anal Pharm Res. 2019;8(1):1–6.
82. R Gobato, MRR Gobato, A Heidari. Evidence of Tornado Storm Hit the Counties of Rio Branco do Ivaí and Rosario de Ivaí, Southern Brazil. Sci Lett. 2019;7(1):9.
83. Moharana Choudhury, Pardis Fazli, Prosenjit Pramanick, et al. Sensitivity of the Indian Sundarban mangrove ecosystem to local level climate change. Parana Journal of Science and Education. 2019;5(3):24–28.
84. Arpita Saha, Ricardo Gobato, Sufia Zaman. Biomass Study of Mangroves in Indian Sundarbans: A Case Study from Satjelia Island. Parana Journal of Science and Education. 2019;5(2):1–5.
85. Nabonita Pal, Arpan Mitra, Ricardo Gobato, et al. Natural Oxygen Counters in Indian Sundarbans, the Mangrove Dominated World Heritage Site. Parana Journal of Science and Education. 2019;5(2):6–13.
86. Ricardo Gobato, Victoria Alexandrovna Kuzmicheva, Valery Borisovich Morozov. Einstein's hypothesis is confirmed by the example of the Schwarzschild problem. Parana Journal of Science and Education. 2019;5(1):1–6.
87. Sufia Zaman, Ricardo Gobato, Prosenjit Pramanick, et al. Water quality of the River Ganga in and around the city of Kolkata during and after Goddess Durga immersion. Parana Journal of Science and Education. 2018;4(9):1–7.
88. Ozan Yarman, Metin Arik, Ricardo Gobato, et al. Clarification of “Overall Relativistic Energy” According to Yarman’s Approach. Parana Journal of Science and Education. 2018;4(8):1–10.
89. Sufia Zaman, Utpal Pal, Ricardo Gobato, et al. The Changing Trends of Climate in Context to Indian Sundarbans. Parana Journal of Science and Education. 2018;4(7):24–28.
90. Suresh Kumar Agarwal, Sitangshu Roy, Prosenjit Pramanick, et al. Marsilea quadrifolia: A floral species with unique medicinal properties. Parana Journal of Science and Education. 2018;4(5):15–20.
91. Ricardo Gobato, Marcia Regina Risso Gobato. Evidence of Tornadoes Reaching the Countries of Rio Branco do Ivai and Rosario de Ivai, Southern Brazil on June 6, 2017. Climatol Weather Forecasting. 2018;6:4.
92. Ricardo Gobato. New Nano-Molecule Kurumi and Raman Spectroscopy using ab initio, Hartree-Fock Method. Am J Biomed Sci & Res. 2019;2(4):AJBSR.MS.ID.000594.
93. DL Graf, Crystallographic tables for the rhombohedral carbonates. American Mineralogist. 1961;46:1283–1316.
94. EN Maslen, VA Streltsov, NR Streltsova, et al. Electron density and optical anisotropy in rhombohedral carbonates. III. Synchrotron X-ray studies of CaCO3, MgCO3 and MnCO3. Acta Crystallographica B. 1995;51:929–939.
95. R Wyckoff. The crystal structures of some carbonates of the calcite group. American Journal of Science. 1920;50:317–360.
96. D Marcus, DE Hanwell, DC Curtis, et al. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. Journal of Cheminformatics. 2012;4:17.
97. J Cioslowski. General and unique partitioning of molecular electronic properties into atomic contributions. Phys Rev Lett. 1989;62:1469.
98. Paul von Ragu Schleyer. Encyclopedia of computational chemistry. New York, J. Wiley, 1998.
99. Mulliken RS. Electronic Population Analysis on LCAO-MO Molecular Wave Functions. I. The Journal of Chemical Physics. 1955;23(10):1833–1840.
100. WJ Stevens, H Basch, M Krauss. Compact effective potentials and efficient shared-exponent basis-sets for the 1st-row and 2nd-row atoms. J Chem Phys. 1984;81:6026–6033.
101. WJ Stevens, M Krauss, H Basch, et al. Relativistic compact effective potentials and efficient, shared-exponent basis-sets for the 3rd-row, 4th-row, and 5th-row atoms. Can J Chem. 1992;70(2):612–630.
102. TR Cundari, WJ Stevens. Effective core potential methods for the lanthanides. J Chem Phys. 1993;98:5555–5565.