For the first time we have demonstrated that, taking into account the interaction of Saturn's magnetic field with the diamagnetic ice particles of the rings, it is possible to explain the separation of particles. It is shown that there is an equilibrium distance between the particles when the force of gravitational attraction between them is compensated by the force of magnetic repulsion. An expression for calculating the equilibrium distance is obtained. It also becomes clear why the ring particles do not stick together.

Keywords: origin of Saturn's rings, magnetic anisotropic accretion, separation of ring particles, equilibrium distance between ring particles, diamagnetism of space ice

After G. Galileo observed the dense rings of Saturn in 1610, for 400 years their origin and observed features still remain a problem of understanding.^1-3 To date, there is not a single gravitational hypothesis of the origin of Saturn's dense rings that would provide a convincing explanation of their origin, the separation of particles and the equilibrium distance between the particles, as well as why the particles do not stick together.^4-7 At the same time, it has recently been demonstrated that Saturn can create rings by itself due to the additional process of magnetic anisotropic accretion (the Tchernyi-Kapranov efrfect) of diamagnetic ice particles of Saturn's protoplanetary cloud if its magnetic field is taken into account.^8-22 Here we try to emphasize the important role of action of the non-gravitational magnetic force of diamagnetic expulsion to explain separation of particles, existence of the equilibrium distance between particles, and why particles do not stick together.^23-26 All these features were observed by the Cassini probe (2004-2017).

The Cassini probe found that particles of dense rings consist of 90-95% water ice^27,28 and the ratio of the heavy and light hydrogen isotopes of the ice of dense rings is the same as for ice on Earth.²⁹ The ice XI is stable below 73K,³⁰ and it is diamagnetic.^31,32 Saturn has a spherically symmetric gravitational field and axisymmetric magnetic field with magnetic equator. The Cassini found the plane of magnetic equator of Saturn almost coincides with geographical one.³³ Dense rings located in the magnetic equator plane. Saturn's magnetic field has a dipolar structure in the region of dense rings.³⁴

The fact that the rings along the orbit are not continuous, but consist of separated particles has already been proved by J. K. Maxwell.^35,36 The study of the separation of ice particles by radius in rings due to their diamagnetism can also make an additional contribution to Maxwell's outstanding analysis. In the magnetic field of the planet, ice particles acquire magnetization and magnetic moment. These are the quantities characterizing the force of interaction with the magnetic field needed to formulate the Newtonian dynamics of the particles, and these quantities for a sole particle differ from those for particles congregated in the rings.  For particles located along the radius, this leads to their repulsion due to the magnetic force. At the same time, the particles are attracted to each other due to the gravitational force. From the balance of the forces of gravitational attraction and magnetic repulsion, an expression can be obtained for the equilibrium and stable distance between the particles in the rings. It is assumed that an ice particle is spherical and uniformly magnetized, which allows solving the magnetization problem in spherical coordinates. To solve the problem of interaction of two identical diamagnetic spheres in an external magnetic field, we use the expression of the magnetization and magnetic moment of one diamagnetic sphere obtained in.¹⁰

Separation of particles and the equilibrium distance between them in the Saturn's dense rings

The force acting on a point magnetic dipole with a moment m₂ in the magnetic field of another point magnetic dipole m₁ at a distance r₀ is³⁷

$F_m=\frac{3{\mu }_0}{4\pi r_0^5}\left[m_2\left(m_1\cdot r_0\right)+m_1\left(m_2\cdot r_0\right)+r_0\left(m_1\cdot m_2\right)-5r_0\left(m_1\cdot r_0\right)\left(m_2\cdot r_0\right)\right]$   (1)

where r₀ is the vector pointing from dipole 1 to dipole 2 (Figure 1).

Figure 1 Parallel magnetic dipoles m₁ and m₂ at a distance r from each other.

Under an assumption that the dipole moments are parallel and equal in magnitude (m),

$F_m=\frac{3{\mu }_0{m}^2}{4\pi r_0^5}{r}_0$   (2)

Substituting the relationship (29) for the induced magnetic dipole moment m obtained in¹⁰

$m=\frac{4\pi R^3{B}_0}{{\mu }_0}\frac{\mu -{\mu }_0}{\mu +2{\mu }_0}$   (3)

Fm of (2) arrives at

$F_m=\frac{12\pi R^6{B}_0^2}{{\mu }_0{r}_0^5}{\left(\frac{\mu -{\mu }_0}{\mu +2{\mu }_0}\right)}^2{r}_0$   (4)

where $B_0$ is the magnitude of Saturn’s magnetic field that magnetizes the particles.

Magnetic field of Saturn’s magnetic dipole in the infinitesimal approximation³⁷ is

$B_0\left(r_{Sp},m_S\right)=\frac{{\mu }_0}{4\pi }\left(\frac{3r_{Sp}\left(r_{Sp}\cdot m_S\right)}{r_{Sp}^5}-\frac{m_S}{r_{Sp}^3}\right)$   (5)

where $r_{Sp}$ is the radius vector from Saturn’s magnetic dipole.

In the magnetic equator plane,

$B_0\left(r_{Sp}\perp m_S\right)=-\frac{{\mu }_0}{4\pi r_{Sp}^3}{m}_S$ ,  (6)

and thus, from (4), the force acting on particle 2 in the equatorial plane is

$F_m\left(r_{Sp}\perp m_S\right)=\frac{3{\mu }_0{R}^6{m}_S^2}{4\pi r_0^5{r}_{Sp}^6}{\left(\frac{\mu -{\mu }_0}{\mu +2{\mu }_0}\right)}^2{r}_0$ .  (7)

If distance between the particles is proportional to their radius, which is the case when the particles are uniformly distributed, the repulsive magnetic force will increase proportionally to the particle volume.

The gravitational attractive force acting on particle 2 with the mass $M_{p2}$ induced by particle 1 with the mass $M_{p1}$ is

$F_g=-\frac{G{M}_{p1}{M}_{p2}}{r_{\text{0}}^3}{r}_0$   (8)

As we can see from (7) and (8) there is a distance between particles when repulsion is prevail on attraction, Figure 2.

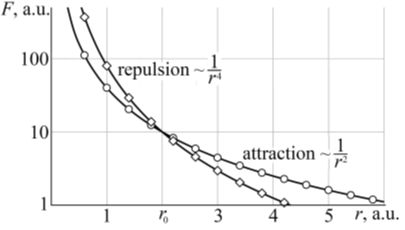
Figure 2 The dependence of the repulsion force and the attractive force on the distance between the particles. At a certain distance ro there is an equilibrium balance in the separation distance between the particles.

If the masses are equal ($M_{p1}=M_{p2}=M_p$ ), the balance of the gravitational and magnetic forces $F_g+F_m=0$ occurs when

$r_0={\left(\frac{R}{r_{Sp}}\right)}^3\frac{m_S}{M_p}\left|\frac{\mu -{\mu }_0}{\mu +2{\mu }_0}\right|\sqrt{\frac{3{\mu }_0}{4\pi G}}={\left(r_{Sp}\sqrt{\frac{4\pi }{3}}\right)}^{-3}\frac{m_S}{{\rho }_p}\left|\frac{\mu -{\mu }_0}{\mu +2{\mu }_0}\right|\sqrt{\frac{{\mu }_0}{G}}$ .  (9)

Thus, the equilibrium balanced distance between particles varies inversely with the particle density ${\rho }_p$ and decreases as the third power of distance from the planet. To calculate the equilibrium distance between particles correctly, it is necessary to know the physical characteristics of dense rings, such as their composition, ice density, magnetic permeability, and others. Certainly, in addition to these forces, centrifugal forces also act on the particles of the ring. However, with a small distance between the particles compared to the radius of the rings, they have almost the same magnitude and do not contribute to a change in the balance of forces.

We have demonstrated that, taking into account the interaction of Saturn's magnetic field with the diamagnetic ice particles of the rings, it is possible to explain the separation of particles. It is shown that there is an equilibrium distance between the particles when the force of gravitational attraction between them is compensated by the force of magnetic repulsion. An expression for calculating the equilibrium distance is obtained. It also becomes clear why the ring particles do not stick together.

None.

Authors declare there is no conflict of interest.

1. Estrada P, Durisen R, Cuzzi J. After the Cassini Grand Finale, Is There a Final Consensus on Ring Origin and Age? AGU Meeting. New Orleans. 2017;298112.
2. Crida A, Charnoz S. Solar System: Recipe for Making Saturn’s Rings. Nature. 2010;468:903–905.
3. Crida A, Charnoz S, Hsu H–W, et al. Are Saturn’s Rings Actually Young? Nature Astronomy. 2019;3:967–970.
4. Fridman AM, Gorkavyi NN. Physics of Planetary Rings: Celestial Mechanics of Continuous Media, Germany: Springer–Verlag; 1999.
5. Schmidt J, Ohtsuki K, Rappaport N, et al. Dynamics of Saturn’s Dense Rings. in  Dougherty M, L. W. Esposito LW, and Krimigis SM. (eds.) Saturn from Cassini–Huygens. 2009;413–458.
6. Charnoz S, Morbidelli A, Dones L, et al. Did Saturn’s Rings Form during the Late Heavy Bombardment? Icarus. 2009;199:413–428.
7. Canup R. Origin of Saturn’s Rings and Inner Moons by Mass Removal from a Lost Titan–sized Satellite. Nature. 2010;468:943–946.
8. Tchernyi V, Kapranov S. How Saturn could create dense rings after the emergence of its magnetic field. The Tchernyi–Kapranov effect: mechanism of magnetic anisotropic accretion. Phys Astron Int J. 2023;7(1):54–57.
9. Tchernyi V, Kapranov S, Pospelov A. Role of electromagnetism in the origin of Saturn’s rings due to diamagnetism of their ice particles:  J.C. Maxwell had almost solved the rings origin problem. URSI Radio Science Letters, 2021;21.
10. Tchernyi V, Kapranov S. Contribution of Magnetism to the Origin of Saturn’s Rings. The Astrophysical Journal. 2020;894(62):6.
11. AAS Journal Author Series: Vladimir Tchernyi on 2020ApJ…894…62T, 2020.
12. Tchernyi V, Kapranov S. Contribution of magnetism to the Saturn rings origin. 2019.
13. The Mystery of Saturn’s Rings Solved by Magnetism? 2019.
14. Tchernyi V, Kapranov S, Pospelov A. Diamagnetic expulsion as a possible cause of the origin and stability of Saturn’s rings. Phys Astron Int J. 2018;2(2):121–126.
15. Tchernyi V, Kapranov S, Pospelov A. Contribution of Electromagnetism to the Saturn Rings Origin and Stability. 235th Meeting of AAS, 3–9 Jan 2020. 385: Sun, Solar System, Milky Way.
16. Tchernyi V, Kapranov S, Pospelov A, Chensky E, Milovanov Yu. Importance of Magnetic Anisotropic Accretion and Quantum Phenomena for the Saturn’s Rings Origin, Formation and Stability of Particles. 43rd COSPAR Scientific Assembly. Sydney, Australia. B0.1, 2021.
17. Tchernyi VV. The Role of Magnetic Field of Saturn for the Rings Origin. Short courses, SC06. XXXIV URSI General Assembly and Scientific Symposium. Rome, Italy. 28 Aug – 4 Sept 2021. 3 h lecture. 2021.
18. Tchernyi VV, Kapranov SV. How Saturn Could Create Rings by Itself. The Third Force of Diamagnetic Expulsion and the Mechanism of the Magnetic Anisotropic Accretion of the Origin of Saturn’s Rings. 2021.
19. Tchernyi VV, Kapranov SV. How Could Saturn form Rings Involving the Third Force of Diamagnetic Expulsion and the Mechanism of Magnetic Anisotropic Accretion. Europlanet Science Congress. 13–24 Sept 2021. EPSC2021–362.
20. Tchernyi VV, Kapranov SV. How Saturn Could Create Rings by Itself. The Role of the Third Force of Diamagnetic Expulsion and the Mechanism of the Magnetic Anisotropic Accretion. 53rd Annual DPS Meeting of the American Astronomical Society, 3–8 Oct 2021. Session: Origins, Formation and Dynamical Systems. 411.07.
21. Tchernyi VV, Kapranov SV. How the Third Force of Diamagnetic Expulsion and the Mechanism of Magnetic Anisotropic Accretion Allowed Saturn to Create Rings by Itself. The Twelfth Moscow Solar System Symposium (12M–S3). Russian Space Research Institute of Russian Academy of Sciences. 11–15 Oct 2021. 12M–S3–SB–12. Abstract Book: 296–297.
22. Tchernyi V, Kapranov S. The role of electromagnetism in the origin of Saturn’s rings. J.C. Maxwell was close to solving this problem. All–Russian conference Radar and Radio Communication. Collection of works. V.A. Kotelnikov IRE of the Russian Academy of Sciences.  November 21–23, Moscow, 2022, 20–25.
23. Tchernyi V, Kapranov S. Modeling of the Saturn’s Rings Origin and Separation of Their Particles. 53rd Lunar and Planetary Science Conference. 7–11 March 2022. The Woodlands, Texas. 53LPSC. W643. No. 1638.
24. Tchernyi V, Kapranov S. The Role of Diamagnetism in the Separation of Particles and Sharp Edges of the Saturn's Rings. 2022.
25. Tchernyi V, Kapranov S. Models of the origin of Saturn’s rings and some problems. 44th COSPAR Scientific Assembly, Athens Greece. B1.1, 2022.
26. Tchernyi V, Kapranov S. Role of Magnetism in the Separation of the Particles of the Saturn’s Rings. The Thirteen Moscow Solar System Symposium (12M–S3). Russian Space Research Institute of Russian Academy of Sciences. 10–14 Oct 2021. 13M–S3–SB–08. Abstract Book: 258–259.
27. Cuzzi JN, Burns JA, Charnoz S, et al. An Evolving View of Saturn’s Dynamic Rings. Science. 2010;327(5972):1470–1475.
28. Esposito LW. Composition, Structure, Dynamics, and Evolution of Saturn’s Rings. Annual Review of Earth and Planetary Science. 2010;38:383–410.
29. Clark RN, Brown RH, Cruikshank DP, et al. Isotopic Ratios of Saturn’s Rings and Satellites: Implications for the Origin of Water and Phoebe. Icarus. 2019;3212:791–802.
30. Hemley R. Effects of High Pressure on Molecules. Annual Review of Physical Chemistry. 2000;51:763–800.  
31. Tchernyi VV, Kapranov SV. To the Problem of the Properties of Ice of the Saturn’s Rings Particles. 238th Meeting of the American Astronomical Society, 7–9 June 2021, Session: Circumstellar Disks and The Solar System, 316.08.
32. Tchernyi VV, Kapranov SV. To the Problem of the Properties of Saturn’s Rings’ Ice. Research Notes of the American Astronomical Society. 2021;5(10):255.
33. Dougherty M, Cao H, Khurana K, et al. Saturn’s magnetic field revealed by the Cassini Grand Finale. Science. 2018;362:6410.
34. André N, Blanc M, Maurice S, et al.  Identification of Saturn's magnetospheric regions and associated plasma processes: Synopsis of Cassini observations during orbit insertion. Reviewes of Geophysics. 2008;46:4.
35. Maxwell J. On the Stability of the Motion of Saturn’s Rings. Monthly Notices of the Royal Astronomical Society. 1859;19:297–304.
36. Brush SG, Everitt CWF, and E. Garber E. (eds.) Maxwell on Saturn’s Rings. Cambridge, MA: MIT Press; 1983.
37. Furlani E. Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications. San Diego, CA: Academic Press; 2001.