
Research Article Volume 2 Issue 2
Diamagnetic expulsion as a possible cause of the origin and stability of saturn’s rings
Tchernyi VV,1
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Kapranov SV,2 Pospelov AY1
1Modern Science Institute, Russia
2AO Kovalevsky Institute of Marine Biological Research, Russia
Correspondence: Tchernyi VV, Modern Science Institute, SAIBR, 20-2-702, Osennii Blvd, Moscow?121614, Russia, Tel 79164268392
Received: February 25, 2017 | Published: March 29, 2018
Citation: Tchernyi VV, Kapranov SV, Pospelov AY. Diamagnetic expulsion as a possible cause of the origin and stability of saturn’s rings. Phys Astron Int J. 2018;2(2):121-126. DOI: 10.15406/paij.2018.02.00073
Download PDF
Abstract
In this work, the problems of a uniformly magnetized sphere in magnetic field are solved for modeling the magnetic properties of Saturn’s rings particles, with the problem of a sphere in an infinite “disk” of evenly distributed identical spheres being formulated and solved for the first time. The found magnetic moments of the spheres are used in deriving the equations of motion of the particles in the gravitational and magnetic field. The solutions of two special cases of these equations indicate that the diamagnetic expulsion in combination with the gravitational attraction to the planet is a plausible cause of stability of Saturn’s rings, and the semi-analytically calculated formation time of the stable orbits is some tens of millennia.
Keywords: saturn rings, outer space superconductivity, diamagnetic expulsion, outer space ice, orthorhombic ice XI
Introduction
To date, the origin and evolution of Saturn’s rings have not been consistently explained. There are several hypotheses concerning the origin of Saturn’s rings, which can be summarized as follows.1 (a) The ring particles can be collision-generated debris from current moons. (b) A satellite in the Roche Zone was destroyed by a passing comet. (c) A massive comet was tidally disrupted during a close passage by Saturn. (d) The rings are the remnants of Saturn’s protosatellite disk. Existing approaches to dynamics of Saturn’s rings2−6 postulate that ring particles orbit the planet close to its equatorial plane without giving a physical explanation of this peculiarity. Other theories explaining stability of the rings in the equatorial plane, for example, by the gravitational quadrupole moment of the planet,7 are in poor agreement with certain characteristics of the rings, e.g. with the particle size distribution.8
In Tchernyi et al.9−12 superconductivity of ring particles was surmised to be a factor determining location of Saturn’s rings in the plane of its magnetic equator, where superconductive particles have a minimum of potential energy. A number of experimental observations of rings’ properties gave evidence of electromagnetic anomalies resembling those of superconductors.13 Still, the question remained as to whether the superconductivity of ring particles was a physical reality.
Saturn’s rings are more than 90 per cent water ice.14 Ice has long been known to be a diamagnetic,15 and it may become superconductive at low temperatures and high pressures, at least in the order of hundreds of GPa.16,17 It is unlikely that such pressures can be reached many thousands of kilometers away from Saturn’s surface, so the hypothesis of macroscopic superconductivity of material of Saturn’s rings appears implausible.
Yet, the expulsion of a magnetic field from macroscopically non-superconductive ice and the concurrent ejection of the ice particles into weak field areas is possible due to a phenomenon of collective quantum proton transfer discovered a few years ago in ice phases with ordered protons in hydrogen bonds.18−20 The concerted proton transfer implies virtually resistance-free transfer of positive charges, which results in persistent current loops. As in the case of superconductors, the magnetic permeabilityof
such materials will tend to zero. In contrast to currents in superconductor, these can persist only in molecular-scale rings consisting of several hydrogen-bonded water molecules. Directed loop currents of such type can be excited, according to Lenz’s law, by applying a magnetic field.
The proton-ordered ice phases are ice II, VIII-XI, and XIII-XV.21,22 All of them, except for orthorhombic ice XI, are high-pressure polymorphs. In contrast to other proton-ordered phases, orthorhombic ice XI is stable at low pressures and temperatures (below ~73 K),22 and it is therefore an appropriate material to form rings in Saturn’s magnetic equator plane. Moreover, partial proton ordering is detected in computer simulations of ice Ic, an intermediate-temperature ice phase,23 and it may be present in Saturn’s rings as well.
The Cassini spacecraft determined that the temperature of Saturn’s rings varies from 70 K to 110 K,24 with middle rings being colder, but at equinox, the temperatures are below 73 K over the entire area of the rings.25 Thus, the temperature of Saturn’s rings is favorable for proton ordering in the ice material of the rings, and it is likely that the emergence of microscopic proton currents at this temperature contributes to orbiting of the ice particles in the magnetic equator plane.
Seeking weak magnetic fields is typical for all diamagnetics, not necessarily superconductors, so the problem of magnetic contribution to the formation of planetary rings can be quite general. Study of electromagnetism and dynamics of particles in the planetary magnetic field may help understand the evolution and sustainability of Saturn’s rings. The aim of this work is considering equations of collision less motion of diamagnetic (and possibly loop-current-supporting) particles in the magnetic field of Saturn and disclosing physical implications through solving particular cases of these equations.
The paper is organized as follows. Section 2 is devoted to magnetostatics of a spherical particle in external magnetic field and simulation of magnetic field of the planet with a thin superconductive disk in the equator plane. In Section 3, the potential energy relationship for a particle in the gravitational and magnetic fields and its equations of motion are derived. The solutions for two important special cases are presented and discussed there. Conclusions are made in Section 4.
Magnetostatics of uniformly magnetized spheres in external magnetic field
Sole uniformly magnetized sphere
From Maxwell’s equation of magnetic field induced around a closed loop is26
. (1)
Then taking into account zero current density (
) and zero rate of change of electric field (
), we obtain
. (2)
In (1),
and
are the vacuum permeability and permittivity, respectively. The zero curl magnetic fields implies existence of a scalar magnetic potential
, the solution of the Laplace equation
. (3)
The general complex solution of (3) in spherical coordinates is
(4)
Where
is the associated Legendre polynomial of degree
and order
, and
and
are constants.
In case of azimuthal symmetry,
and
. (5)
Taking into account that the potential must be finite in the centre of the sphere and at infinite distance from it, the relationships for the potential inside (
) and outside (
) the sphere differs in the radial function:
, (6)
and
. (7)
Where R is the radius of the sphere. Magnetic field intensity is the negative gradient of the scalar magnetic potential:
. (8)
Its radial component has discontinuity at
due to the non-zero magnetic surface charge density
, which is found from the magnetization M using Gauss’s theorem:
. (9)
Then,
(10)
and, from (6)-(10),
. (11)
For this equality to be fulfilled, the only non-zero term in the sums in (11) must be that with
. Then,
. (12)
Another boundary condition is the continuity of the magnetic potential at the surface of the sphere (at
):
, (13)
Whence, taking into account (6), (7) and
,
. (14)
Alternatively, this relationship can be obtained from the continuity of the tangential components of the magnetic field intensity. Then, from (12) and (14), the integration constants are
(15)
and
. (16)
By definition, magnetic moment m per unit volume is the magnetization:
. (17)
Then, the magnetic potential in (6) and (7) can be written as
, (18)
And
. (19)
The magnetic field intensity inside the sphere is
, (20)
and that outside the sphere is
(21)
Where
and
are the radial and polar unit vectors of the spherical coordinate system.
Let the magnetized sphere be placed in an external magnetic field
with intensity
. The total magnetic field inside the sphere is the sum of the external magnetic field and the fields due to the induced current and magnetization:
, (22)
and the total magnetic field intensity is
. (23)
Because the total magnetic field is proportional to the total magnetic field intensity
(24)
With the absolute permeability
as the proportionality factor, it follows from (22)-(24) that
, (25)
Whence
(26)
and
. (27)
From (26) and (27) it is clear that magnetization and magnetic moment of diamagnetic spheres are directed oppositely to the external field. Among diamagnetics, the largest absolute values of these properties are demonstrated by superconductors, which have
NA-2, magnetization
, and magnetic moment
.
Uniformly magnetized sphere in a magnetized “disk” consisting of identical spheres
Let a magnetized sphere be placed amidst identical magnetized spheres forming an infinite “disk”. Such a disk is a model of dense planetary rings such as those of Saturn. We assume that the spheres are distributed uniformly in hexagonal arrangement with the planar density
.
Each sphere will then experience magnetic fields of all other spheres with the magnetic dipole moments m. If the disk is tilted at an angle
=to the magnetic equator plane and the distance from the sphere centre to the edge of the disk is
, the magnetic field intensity of the magnetized disk exerted on a sphere in it is
(28)
Here the integration is performed over the area of the disk, which is assumed continuous. Then, by analogy with (22) and (23), the total magnetic field inside the sphere is
, (29)
and its intensity is
. (30)
By analogy with the derivation of (26) and (27), it is easy to find the magnetization
(31)
and the magnetic moment
. (32)
For superconductors, the magnetization in this case reduces to
and the magnetic moment becomes
. The absolute values of magnetization and magnetic moment are higher than those obtained for a sole sphere, and the force of diamagnetic expulsion into the weak-field areas in this case will be stronger.
Simulation of magnetic field of a planet with a uniform superconductive disk
Comsol Multi‒physics software has been used to simulate the magnetic structure of Saturn and its magnetosphere. The red sphere (Figure 1A) representing the metallic hydrogen interior of Saturn27 has a uniform magnetization. A superconducting disk modeling Saturn’s rings is in the plane of magnetic equator of the planet whose equatorial surface field is about 20μT.28 In Figure 1A, the simulation results for z-component of magnetization, normal component of the magnetic flux density and magnetic field of Saturn are presented. The disk is thin (0.01 of the radius). The shell over it has the relative permeability 2. The vertical red line represents the line along which the z-component of the magnetic flux density is plotted in Figure 1B.
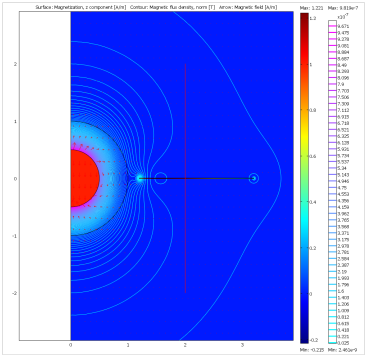

Figure 1
- Simulated magnetic structure of a planet with metallic magnetic core and superconductive disk in the magnetic equator plane. Surface: z-component of magnetization, contour: normal component of the magnetic flux density, arrows: magnetic field.
- z-component of the magnetic flux density along the vertical red line in Figure 1a.
The disk significantly modifies the magnetic field of the sphere. If we consider a superconducting particle flying in the vicinity of the disk, the magnetic well will eventually attract the particle to the disk. In z-direction the well is not quadratic but rather cusp-like (triangular), and this is consistent with the small thickness of main rings of Saturn (around 10 m).
Potential energy and equations of motion of magnetized spheres
The magnetic moment relationships in (27) and (32) has the form
(33)
Where
is the parameter depending on the magnetic properties and size of the spheres. For diamagnetics
.
The potential energy
of a magnetized sphere with the mass
in the magnetic and gravitational field is
(34)
Where
kg is the mass of the planet and
m3∙kg-1∙s-2 is the gravitational constant.
The force acting on the sphere is the negative gradient of the potential energy:
(35)
Where
is the acceleration. In spherical coordinates, the equations of motion are29
(36)
Equations (36) cannot be solved analytically. At the same time, direct numerical integration of (36) generating long-term, on a cosmic scale, solutions is neither feasible nor informative because one needs to integrate over thousands of oscillations with only one set of initial conditions. For this reason, we will confine ourselves to considering several important consequences arising out of the equations of motion. Consider several special cases of these equations.
- Particles orbiting at equal distance from the centre (r =const) with neglect of magnetic force (C= 0)
This is the case of classical motion around the planetary centre of mass. The equations of motion is in (36) are then reduced to
(37)
From the first and second equations in (37), the following one is obtained:
, (38)
which has the solution
(39)
With the initial angle
at
.
The azimuthal velocity is then equal to
. (40)
The initial velocity
should be sought from the thickness
of Saturn’s main rings (
m). Expanding (39) in the series near
, one obtains
, (41)
Whence the difference
between the maximal and minimal polar angles is
. (42)
Hence,
. (43)
Equation (43) gives the initial angular velocity 1.7∙10-12 s-1 at the mean ring radius of 105 000 km, which corresponds to the linear velocity of 0.2 mm∙s-1. This value is in a striking disparity with the Keplerian orbital velocity from (40) at the same radial distance:
19 km∙s-1. It is improbable that colliding ring particles of imperfect shape have such different components of the velocity.
On the other hand, assuming the velocity components to be comparable, i.e.
, we arrive at
, a triangular periodic function of time with the extreme values of 0 and
, which is inconsistent with the flat structure of the rings.
- Magnetized particles orbiting at equal distance from the centre (r = const)
In this case
and the equation of the polar coordinate variation is
. (44)
Using the MuPAD symbolic calculation tool of Matlab environment, we arrive at the following solution of (44):
. (45)
The azimuth velocity in this case is
, (46)
Which emphasizes that the gravitational force is counterbalanced not only by the centrifugal one, but also by the force of diamagnetic expulsion. The result given in (45) accounts for the fact that rings of Saturn are essentially planar and lie in the plane of its equator.
As the next task, it is possible to estimate the time period over which the magnetic force will significantly modify the orbit of a particle driving it into the magnetic equator plane. The gravitational force acting on a particle is almost perfectly counterbalanced by the centrifugal force and the particle is very slowly approaching the planet (
). Then, the period of orbiting at a distance
from the centre is
.
On the assumption of the distances traveled by the particle in the
- and
-directions being proportional to the corresponding forces, the ratio of the right-hand sides of the second and first equations in (36) gives the dimensionless acceleration, and it is tangent of the angle through which the particle’s orbit has rotated over a certain time. Because the tangent is small, this ratio is approximately the orbit rotation angle. The dimensionless time needed to rotate the orbit through the mean angle
is
. Then, using the ratio of the forces from (36), one can obtain the following approximate equality:
(47)
Where the products of the harmonic functions were replaced by their averages over the angle range
. Let the orbit radius be
105 000 km and the particle is an ice sphere with the magnetic moment
(see Section 2.1), radius 1 m and density 934 kg∙m-3 at ‒180°C30 so that its mass is
kg. Then, the time of the orbit plane rotation is
s, which corresponds to
years. This value can be treated as the time of formation of stable orbits of Saturn’s main middle rings, and it is in reasonable agreement with the recent estimates.31
Conclusion
In this work, we have studied magnetostatics and dynamics of magnetized spheres in the spherically symmetric gravitational and axially symmetric magnetic field of Saturn. For the first time, the magnetization and magnetic moment of a sphere placed in an infinite “disk” of evenly distributed identical spheres modeling Saturn’s dense rings in its magnetic field have been found. The magnetic force acting on a sphere in the “disk” of magnetized spheres proves to be stronger than that acting on a sole sphere.
Simulation of magnetic characteristics in the system of a finite superconductive disk in the magnetic field of Saturn has shown that this disk significantly modifies the structure of the magnetic field and attracts the diamagnetic particles, thus increasing the mass of the disk. The superconductivity of the disk is involved to simulate the system of Saturn’s rings because the particles of the low-temperature ice phase, as emphasized in Introduction, may demonstrate some typical properties of superconductors in magnetic field such as existence of resistance-free loop currents and expulsion of magnetic field out of the ice material. The sustainability of the proton loop currents in the proton-ordered ice XI can explain the sharp edges of the rings: temperature increase observed at both edges stimulates the phase transition to a proton-disordered ice modification which has higher magnetic permeability, the diamagnetic expulsion force of this ice phase becomes much weaker, and the respective orbits are no longer stable.
Derivation of the potential energy relationship for the spherical particles in the gravitational and magnetic fields has led to formulating the equations of collision less motion of the ring particles. Two special cases of these equations have been considered: with and without the magnetic force at constant radial distance from the centre. In the gravitational field only, the solution of the equations of motion yields the ratio of angular velocity components that turns out to be extremely unlikely, which speaks against the purely gravitational approach to Saturn’s rings. Furthermore, if the magnetic force is taken into account, the location of circular orbits of the particles in the magnetic equator plane consistently follows from the equation solution.
Finally, we have estimated the formation time of stable orbits of Saturn’s rings (some tens of millennia) and found it consistent with the recent estimates. All the results obtained suggest that the additional force of diamagnetic repulsion of ice particles stabilizes their orbits in the plane of magnetic equator of Saturn.
Acknowledgements
Conflict of interest
Authors declare there is no conflict of interest.
References
- Charnoz S, Morbidelli A, Dones L, et al. Did Saturn's rings form during the Late Heavy Bombardment? Icarus. 2009;199(2):413−428.
- Fridman AM, Gorkavyi NN. Physics of Planetary Rings: Celestial Mechanics of a Continuous Media. Germany: Springer−Verlag; 1999.
- Esposito LW. Composition, structure, dynamics, and evolution of Saturn’s rings. Annual Review of Earth and Planetary Sciences. 2010;38:383–410.
- Schmidt J, Ohtsuki K, Rappaport N, et al. Dynamics of Saturn’s dense rings. In: Dougherty M, editor. Saturn from Cassini−Huygens, Chapter 14. Netherlands: Springer Science+Business Media BV; 2009. p. 413−458.
- Goldreich P, Tremaine S. The dynamics of planetary rings. Annual Review of Astronomy and Astrophysics. 1982;20:249−283.
- Borderies N, Longaretti PY. Description and behavior of streamlines in planetary rings. Icarus. 1987;72(3):593–603.
- Tsygan AI. What maintains Saturn's rings? Soviet Astronomy. 1977;21(4):491−494.
- Brilliantov N, Krapivsky PL, Bodrova A, et al. Size distribution of particles in Saturn’s rings from aggregation and fragmentation. Proceedings of the National Academy of Sciences of the United States of America. 2015;112(31):9536−9541 .
- Tchernyi VV, Pospelov AY. Possible electromagnetic nature of the Saturn's rings: superconductivity and magnetic levitation. Progress In Electromagnetic Research, PIER. 2005;52:277−299.
- Tchernyi VV, Chensky EV. Movements of the protoplanetary superconducting particles in the magnetic field of the Saturn lead to the origin of the rings. IEEE Geoscience and Remote Sensing Letters. 2005;2(4):445−446.
- Tchernyi VV, Chensky EV. Electromagnetic background for possible magnetic levitation of the superconducting rings of Saturn. Journal of Electromagnetic Waves and Applications. 2005;19(7):1997−2006.
- Tchernyi VV, Pospelov AY. About hypothesis of the superconducting origin of the Saturn’s rings. Astrophysics and Space Science. 2007;307(4):347−356.
- Tchernyi VV. About role of electromagnetism to the Saturn rings origin–to the unified theory of the planetary rings origin. International Journal of Astronomy and Astrophysics. 2013;3(4):412−420.
- Cuzzi JN, Burns JA, Charnoz S, et al. An evolving view of Saturn’s dynamic rings. Science. 2010;327(5972):1470−1475.
- Senftle FE, Thorpe A. Oxygen adsorption and the magnetic susceptibility of ice at low temperatures. Nature. 1962;194:673−674.
- Babushkina GV, Kobelev LY, Yakovlev EN, et al. Electrical conductivity of ice under high pressure. Physics of the Solid State. 1986l;28(12):3732–3734.
- Flores−Livas JA, Sanna A, Graužinytė M, et al. Emergence of superconductivity in doped H2O ice at high pressure. Scientific Reports. 2017;7:6825.
- Bove LE, Klotz S, Paciaroni A, et al. Anomalous proton dynamics in ice at low temperatures. Physical Review Letters. 2009;103(16):165901.
- Yen F, Gao T. Dielectric anomaly in ice near 20 K: evidence of macroscopic quantum phenomena. The Journal of Physical Chemistry Letters. 2015;6(14):2822–2825.
- Drechsel−Grau C, Marx D. Collective proton transfer in ordinary ice: local environments, temperature dependence and deuteration effects. Physical Chemistry Chemical Physics. 2017;19(4):2623−2635.
- Savage H. Water structure in crystalline solids. Water Science Reviews 2. In: Franks F, editor. UK: Cambridge University Press; 1986.
- Lobban C, Finney JL, Kuhs WF. The structure of a new phase of ice. Nature. 1998;391(6664):268−270.
- Geiger P, Dellago C, Macher M, et al. Proton ordering of cubic ice Ic: spectroscopy and computer simulations. The Journal of Physical Chemistry C. 2014;118(20):10989–10997.
- https://www.nasa.gov/mission_pages/cassini/media/cassini−090204.html
- Spilker L, Ferrari C, Morishima R. Saturn’s ring temperatures at equinox. Icarus. 2013;226(1):316−322.
- Jackson JD. Classical Electrodynamics. 3rd ed. USA: Wiley; 1999.
- Smoluchowski R. Metallic interiors and magnetic fields of Jupiter and Saturn. Astrophysical Journal. 1971;166 (6):435−439.
- Russell CT, Dougherty MK. Magnetic fields of the outer planets. Space Science Reviews. 2010;152(1−4):251–269.
- Shapiro IL, Berredo−Peixoto GD. Lecture Notes on Newtonian Mechanics: Lessons from Modern Concepts. USA: Springer; 2013.
- CRC Handbook of Chemistry and Physics. In: Lide DR, editotr. 86th ed. USA: CRC Press; 2005.
- Tcherny VV, Pospelov AY. Superconductivity of Saturn rings: Quantum locking, rings disc thickness and its time creation. Journal of Modern Physics. 2018;9(3):419−432.

©2018 Tchernyi, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.




