In this paper, we will consider Navier-Stokes problem and it's interpretation by hyperbolic waves, focusing on wave propagation. We will begin with solution for linear waves, then present problem for non-linear waves. Later we will derive for numerical solution using PDE`s. We can conclude that although the numeric solution for partial derivative equations can give a correct result, it is not always describing a physical phenomenon

Keywords: navier-stokes problem, hyperbolic waves, wave propagation, linear wave, non-linear waves

Discretization – method which involves dividing to small pieces in order to solve

Shock waves – abrupt jumps in density, velocity and pressure

Hyperbolic wave – wave mathematically formulated through hyperbolic partial differential equations is called hyperbolic wave

Newton's second law is F = ma. It says Force (F) on an objects equal to mass (m) multiplied by acceleration (a)

Diffusing viscous term – describes the physical transfer quantity through a small area with normal velocity per some time.

Viscous flow – Viscosity describes fluids resistance to deformation caused by stress (can be shear stress or tensile stress).  Equivalent term for metals would be thickness

Shear stress is given by a formula F/A, where F is force and A is cross sectional area of material with area parallel to the applied force vector.  It is applied to fluids which move along solid boundary.

Tensile stress– In fluid tensile stress describes the internal force applied on a given particle, caused by neighboring particle.

Problem setting and description

Navier-Stokes equations are designed in order to simulate the flow of various fluids in numerous disciplines across physics (electromagnetism, acoustics, elasticity). Navier- Stokes equations were formed by combining Newton's second law and fluid motion. Also assumption of stress being the sum of diffusing viscous term and pressure term was taken to describe viscous flow. Without Navier-Stokes equations working with weather model, ocean currents, water flow in a pipe, air flow around a wing would be extremely hard. Also these equations are widely used in designing airplanes and cars, studying blood flow, designing power stations, analysing pollution and so on.

History of the Navier-Stokes equations dates back to 1822. Claude-Louis Navier mentioned in his memoir the equations for homogeneous incompressible fluids with regards to molecular arguments. Later, in 1829 Poisson derived equations for compressible fluids. Consequentially, George Gabriel Stokes formulated the Navier-Stokes equations in his paper (1847) as we know it today.

Up to this day there is no proof for existence and uniqueness of Navier-Stokes equations' solution in three dimensional space. Moreover, it is considered one of the seven most important unsolved problems currently. Clay Mathematical Institute offers a significant prize of one million dollars to the person who will prove this or bring a counter-example. Although a number of advancements have been made in this sphere, yet it remains mainly a “dark forest” for the researches. As you will see in this paper, there is a perfectly working solution for both one dimensional case and two dimensional case.

This paper illustrates Navier-Stokes hyperbolic wave equations, its solutions in one dimensional case, and extending that solution for two dimensional cases. The solution for one dimensional case is rather simple, in contrast the two-dimensional case requires more work. In following paper we focused on solution by using partial differential equations. Explicit finite difference approximation was used for that purpose. In the end we bring wave propagation examples, with both two dimensional and three dimensional figures.

Hyperbolic Waves

In our paper we are interested in hydrodynamic equations which are similar with signal-propagation equations. That specific kind of equations are called hyperbolic equations. Also hyperbolic equations have much broader use, and can be met elsewhere, we will concentrate on them used in hydrodynamics only. The simplest hyperbolic equations are given by the following equation.

$\phi \text{tt}=c^{2}0{\nabla }^2 \left(0\right)$

Where φ is a function φ(x, t), c0 is constant velocity, and ∇²= ∇f=Σ^n∂2f2. In (2.2) we will derive the $i=0^{\partial }{}^{x}i$  Following formula, representing hyperbolic waves in one dimensional case.

$\Phi {\text{t+c}}_{\text{0}}.{\phi }_x=0$   (1)

(1) is the common equation for linear waves. Here (x, t) is a function which describes time depending shifting of the function φ along x which has a velocity c0. That is it describes the propagation of the wave.

Let's understand difference between linear waves and non-linear. In linear waves the velocity at any point is the same. That is, the total velocity of the flow is not effected from internal particle velocities (which we will see are the case in non-linear). So if we look at Figure 1, we'll see that the wave repeats itself and it propagates without any change at any moment in time. If we would pick any point and examine it during time, the overall velocity in that point will always be the same. For example, imagine that you are in the middle of the ocean. Waves are born and start their propagation. From that point waves are linear as they acquire some height and just propagate without changing their shape.

Figure 1 Non-linear wave propagating.

What about nonlinear waves, we will rarely observe too similar curvatures at two different moments. Particles in one position have higher velocity than in others, thus during the time we reach a point when some particle x, reaches particle y, which was in front before, then passes it. We will have then a picture of crushing wave. For instance, imagine you are on the beach. You see the waves coming, then crushing on the sand. Such waves are not linear, as they change their shape over time. In Figure 2 you can see nonlinear wave. As in computers for crushing wave one x would require three y values, it is not display, instead such image is resulted the last one also can be represented as

Figure 2 Non-linear wave with grainy surface after some time.

$\frac{\partial \phi }{\partial t}=\underset{\text{x}\to \text{0}}{\lim }\frac{\phi \left(t+\Delta t, x\right)-\phi \left(t, x\right) }{t}\approx \frac{\phi \left(t+\Delta t, x\right)-\phi \left(t, x\right) }{t}$   (2)

and

$\frac{\partial \phi }{\partial x}=\underset{\text{x}\to \text{0}}{\lim }\frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x\right) }{x}\approx \frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x\right) }{x}$   (3)

the last one also can be represented as

$\frac{\partial \phi }{\partial x}=\underset{\text{x}\to \text{0}}{\lim }\frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}\approx \frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}$   (5)

Thus, to not be biased to the right or left, we write it in following way

$\underset{\text{x}\to \text{0}}{\lim }\frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}\approx \frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}$   (6)

plugging this into (5) we get

$\frac{\phi \left(t+\Delta t,x\right)-\phi \left(t, x\right) }{t}-\zeta \frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}=0$   (7)

physical meaning of this equation is the propagation of non-linear wave, however in some parts the amount of error can cause grainy (non- smooth) surface in the graph. As can be seen from Figure 3 the wave propagating over time starts to destabilize due to computational-error accumulation.

Figure 3 Linear wave propagation.

Numerical background and step by step algorithms

For 1D case no special calculating method must be introduced as it is solved analytically by using, solution that is presented in 2.2.

$\phi \left(x\right)=f\left(x-c_o. t\right)$

However, when we get to solve the PDE for the non-linear wave propagation, there is a methodology to be presented. As we already presented in figure & description 2.3 when having a hyperbolic PDE of type

$\underset{\text{x}\to \text{0}}{\lim }\frac{\phi \left(t+\Delta t,x\right)-\phi \left(t, x\right) }{t}-\zeta \underset{\text{x}\to \text{0}}{\lim }\frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}=0$

we can approximate it by neglecting the limit and taking a small Δt and Δx. As we do we get the approximation

$\frac{\phi \left(t+\Delta t,x\right)-\phi \left(t, x\right) }{t}-\zeta \frac{\phi \left(t,x+\Delta x\right)-\phi \left(t, x-x\right) }{2x}=0$

After getting this equation lets divide our coordinate system into an n by m grid where where the difference between each to xi neighbors is Δx and ti  neighbors Δt.

Now having this grid we can rewrite the equation we got in the following form

$\frac{\phi \left(t_{i+1}, x\right)-\phi \left(t, x\right)}{t} -\zeta \frac{\phi \left(t, x_{i+1}\right)-\phi \left(t, x_{i-1}\right)}{2 x} =0$

From here, given the initial condition (row φ(0,x)), we want to find the values of each row to reconstruct the wave at each point of time. That is we need to find φ(ti+1,x). Lets get it from the equation above.

$\phi \left(t_{i+1},x\right)=t \cdot \zeta \frac{\phi \left(t_{i+1},x\right)-\phi \left(t_{i+1},x\right)}{2x}+\phi \left(t,x\right)$

Here is the numerical solution for the The PDE that we intended to solve. As one can notice this scheme can have a problem at the boundaries. Numerous methods have been developed to approximate and solve that problems. The famous schemes are Lax-Wander of, leap-frog ect. ect.

Numerical solution of navier-stokes for linear waves

The numerical solution in the this case involves just using the analytical solution and simulating time in order to get the wave propagation. One just needs to assign $\phi (x)=f(x-c_0\cdot t)$ and correctly simulate the propagation of wave with the constant speed c0. For this simulation one can use the horizontal translation of the function by c0t. As one can see from Figure 4 the wave propagates with constant speed. The periodic for of the wave is the obvious assertion for the abovementioned words. Also no uncouthness or error cumulating is theoretically possible in this case, due to the fact that the solution for the equation is derived analytically.

Figure 4 Non-linear wave at two different time instances.

Numerical solution of navier-stokes for non-linear waves

In this section we will speak about main aim of this paper, the solution of two dimensional that is non-linear waves. As was mentioned in the previous chapter we will derive solution by PDEs. First let's understand what we have and what we want to get. We have the function at the initial moment (t=0), and we want to be able to trace how it would behave during some given period. Also we have function $\zeta$ which describes the velocity change for the individual particle at the given time moment.

(7) shows relation we had derived. For our purpose we will have to approximate the initial function at each next stage by result of the previous step. To make it more clear let's examine Figure 5. In the given example we have propagation of function sin(x2) at two moments. Also we are looking at the range $\left[0,4\pi \right].$ As we see the waves are similar however they slightly differ at the endpoints. The reason for alternative propagation is mainly because of. In the figure it is defined by x+t, which forces the wave to change its shape. The change in the wave is seen much better in Figure 6 which demonstrates the wave in 16 different time moments. Two different view are presented to show the difference in

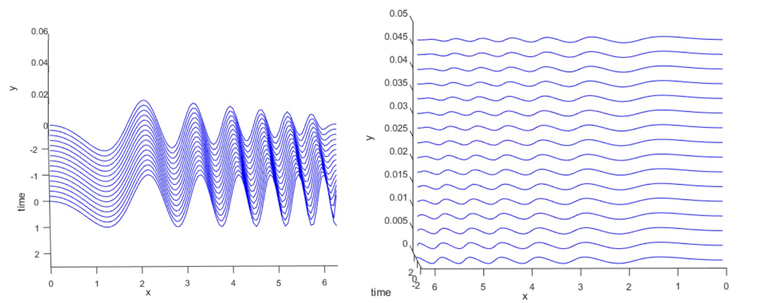
Figure 5A,B Non-linear wave at many time instances & Point construction of the function at next time moment.

Figure 6 Propagation of the linear wave constructed by function oneD.

For one dimensional case our results are very stable. First let's examine function sinx with constant speed 1 on [0,4π], given t=10. Figure 7 is the plot by using OneD function. As we see our wave propagates without any error. Figure 7 A is the plot using function tp1, as we see even for linear waves there exist an error caused by approximation of border points. Figure 7B again there is no error in propagation. tp2 is used. Figure 8A,B this figures illustrates the propagation of wave constructed by tp3 in different time moments in 2D and Figure 9A,B illustrates the propagation of wave using tp4. Error accumulation is obvious. There is no need for further exploration of linear wave case, thus we will move on to two dimensional case.

Figure 7A,B Propagation of the linear wave constructed by function tp1 & Propagation of the linear wave constructed by function tp2.

Figure 8A,B This figures illustrates the propagation of wave constructed by tp3 in different time moments in 2D.

Figure 9A,B Illustrates the propagation of wave using tp4. Error accumulation is obvious.

From Figures illustrated in Section 4.2 can be concluded that even though some times the numeric solution for partial derivative equations can give a correct result, it is not always describing a physical phenomena. As Waves simply cannot behave in nature as for example in figure 4.2 Few Things can be noticed. First there are cases when error occurs, but later it is self fixed and the continuation is normal.( For instance Figure 4.2 Describing ex with ζ = x). Another thing that can be noticed is that Waves are inclined to the right, which is mainly caused by our method, double use of the same point). There are ways which can make this solution more realistic. That is making small Δt and/or Δx. However it will result in slower calculation. There are known ways for stable Calculations. One of such methods is presented by Suren Khachatryan in the paper “Modification of the Method of Integration along Characteristics as Adaptive Mesh Approach in Solution of Hyperbolic and Parabolic PDEs”.

None.

None.

The author declares there is no conflict of interest.

1. Whitham G. Linear and nonlinear waves. New York: Wiley. 1974.
2. Josheph D, Funada T. Potential flows of viscous and viscoelastic fluids. Cambridge niversity Press. 2007.
3. Lynch L. Numerical Integration of Linear and Nonlinerar Wave Equations. DIssertations, Theses, and Student Research Papers in Mathematics. Paper 16. Florida Atlantic University. 2004. p. 1–149.