Recent observations of the James Webb Space Telescope (JWST) seem to show that structure formation and the build-up of planetary systems in the universe already must have started astonishingly enough at a time of 0.1 Gigayears after the Big-Bang. The question thus arises whether these earliest planetary systems did originate under similar conditions as did our solar system about 4.1 Gigayears later? In this article we are looking onto this fundamental problem and show that for the context of the origin of solar systems it very much counts how the Hubble expansion of the universe has developed over cosmic eons. If the cosmic expansion dynamics is too large, no solar systems at all would have been produced, if it would be too small, solar systems would have originated just shortly after the cosmic matter recombination, but not anymore since then.

In other words, the Keplerian laws, derivable with the help of Newton‘s gravitational law, would they perhaps reflect the changes in an expanding universe over the cosmic eons? And if yes, - how would they do it? In this article we conclude that in fact Newton‘s pendulum or Kepler‘s planetary revolution periods represent a perfect cosmic clock indicating the actual status of the expanding universe. Only in case, however, that Newton‘s gravitational constant G would vary with the scale R of the universe like G - R, then this clock astonishingly enough would be synchronized for the whole cosmic evolution not serving anymore as a cosmic tracer.

How does the initial matter uniformity disappear in an expanding universe?

It is hardly understandable why cosmic matter with, - as generally required by the cosmologic principle -, an initially perfectly homogeneous distribution in space may at all have started at some epoch in the past a process of forming local material substructures like stars or galaxies. Such formations are generally understood as driven by local, gravitationally induced collapse instabilities of cosmic gases forming large local units of solar or Giga-solar masses. In an expanding universe the uniformly distributed cosmic matter should otherwise simply be subject to an ongoing redistribution into a permanently growing cosmic space, accompanied by permanently and unavoidably decreasing cosmic mass densities $\rho (R)={\rho }_0\cdot {(R_0/R)}^3$ . The opposite can only be expected, if the collapse period of a gravitationally induced local structuring process is shorter than the universal expansion period of the homogeneous matter distribution, so that density structures can form and do grow decoupled from the general cosmic expansion. The problem thus evidently is and must be closely connected with the specific form of the actual expansion dynamics of the whole universe, permitting matter to accumulate at distinct places, even though the universe continues to expand.

Given an accelerated expansion of the universe, as is presently favoured by several astrophysicists when trying to understand the redshifted emissions of most distant galaxies^1-3 it may be definitely harder to understand these structure formation processes. Here in this article we, however, mainly consider this problem on the basis of a "coasting expansion of the universe" with a constant expansion velocity of its scale $R=R(t)$ with $\dot{R}=const$ and $\ddot{R}=0$ . This latter form of the cosmic expansion we do strongly favour in this article since it can be based on solid scientific grounds.^4,5

Why is the Hubble parameter a critical quantity?

Before the event of cosmic matter recombination anyway no gravitationallly induced matter collapses were possible, because then ionized matter - because of strong electron-photon couplings - was repelled by the collapse-inherent increase of radiation pressure. Thus the question arises, how much variation the Hubble parameter $H=H(t)$ may have undergone since that cosmic time of matter recombination when at first in cosmic history matter accumulation or condensation could have started? What in fact does one know at all about the value of the Hubble parameter at earlier times in the cosmic past, especially near and even before the point of recombination of cosmic matter? To frankly confess the truth: Not very much, - and for sure - nothing safe yet.

All about that is connected with the mainstream cosmic view which cosmologists nowadays share concerning the state of the universe near cosmic recombination time. One can only speculate about this point on the basis of the Big-Bang cosmology, and perhaps question whether it existed at all in the history of the universe, i.e. if at all cosmic matter at some times in the past was in a fully ionized phase. The present day value of the Hubble parameter with $H_{today}=70km/s/Mpc$ .⁶is obtained from redshift observations of the more or less nearby galaxies with redshifts $z\le 1$ , and not very much can be speculated from this poor observational basis on the specific value of $H_r=H(t_r)$ which prevailed at the time of recombination $t=t_r$  (i.e. ${\rm Z}\simeq {10}^3$ ). If to the contrary at least some fundamental theoretical prerequisites need to be fulfilled, then at least the basis for estimations would be better.

For example: If the Hubble parameter H is predetermined for all cosmic times by a constant vacuum energy density $\Lambda$ , at present time as well as back all the time till the recombination time $t=t_r$ , then it can be shown (see Fahr, 2021a) , that the Hubble parameter would have been constant all over this time period from the recombination period till now, i.e. $H_{\Lambda }=H_{today}=H_r$ . That would mean concerning the above relation that $H_r=H_{today}$ ! If, however, the Hubble parameter at present times, as well as at the recombination time $t_r$ , is purely determined by baryonic matter, i.e. by the rest-mass density of baryonic matter $\rho ={\rho }_B(R)$ , then one could use the following relation taken from the first of the two Friedman equations⁷ and obtain:

$H^2(R)=\frac{8\pi G}{3}{\rho }_B(R)$

Concerning the corresponding Hubble parameter at the recombination epoch at $t=t_r$ with $R_r={10}^{-3}{R}_{today}$ ⁸one would then obtain a value:

$H_r=H_{today}\cdot {(\frac{R_{today}}{R_r})}^{3/2}=H_{today}\cdot {(\frac{{10}^3{R}_r}{R_r})}^{3/2}={10}^{4.5}{H}_{today}$

meaning that the Hubble parameter at the recombination era could under this prerequisites certainly have been much larger than the present day Hubble parameter $H_{today}$ .

For a more general study of the historic evolution of the Hubble parameter $H=H(t)$ one should, however, start from a broader, more general analytic basis by again looking back to the first of the Friedman equations,⁷ when expressing the fact that the Hubble parameter in a more general outline is given by:.

$H^2=\frac{R^2}{R^2}=\frac{8\pi G}{3}[{\rho }_B+{\rho }_D+{\rho }_v+{\rho }_{\Lambda }]$

where all quantities denote equivalent mass densities $[{\rho }_B+{\rho }_D+{\rho }_v+{\rho }_{\Lambda }]$ of baryonic matter, of dark matter, of photons, and of the vacuum energy. These quantities are thought to be known as functions of time t, or equivalently, of the scale of the universe $R=R(t)$ , though at least the quantities ${\rho }_D$ and ${\rho }_{\Lambda }$ are physically not at all well conceived, neither by its concrete meaning nor by its dependence on the scale R of the universe.

By introduction of ${\Omega }_0=3H_0^2/8\pi G$ with $H_0$ denoting the present-day Hubble parameter one can write the upper equation in the following form:

$1=\frac{1}{{\Omega }_0}[{\rho }_B+{\rho }_D+{\rho }_v+{\rho }_{\Lambda }]=[{\Omega }_B+{\Omega }_D+{\Omega }_v+{\Omega }_{\Lambda }]$

For the present cosmic epoch one has obtained observational best-fit values for the above quantities ${\Omega }_B+{\Omega }_D+{\Omega }_v+{\Omega }_{\Lambda }$  given by^2,6 with the following numerical values:

${\Omega }_B=0.04;\mathrm{....}{\Omega }_D=0.23;\mathrm{....}{\Omega }_v=0.01;\mathrm{....}{\Omega }_{\Lambda }=0.72$

Inserting now in addition the expected dependences of ${\rho }_B;{\rho }_D;{\rho }_v;{\rho }_{\Lambda }$ on the scale of the universe leads us then to the following expression:

$H^2=\frac{R^2}{R^2}=H_0^2\cdot {\Omega }_B{(\frac{R_o}{R})}^3+{\Omega }_D{(\frac{R_o}{R})}^3+{\Omega }_v{(\frac{R_o}{R})}^4+{\Omega }_{\Lambda }]$

Hereby the equivalent mass energy density ${\rho }_v$ of the cosmic photons has been taken into account by its value corresponding to a cosmologically redshifted Planck radiation.⁹ When introducing the present-day $\Omega$ -values into the upper equation, one then obtains the R-dependence of the Hubble parameter in the following form (Figure 1):

$H(R)=H_0\cdot \sqrt{0.27{(R_0/R)}^3+0.01{(R_0/R)}^4+0.72]}$

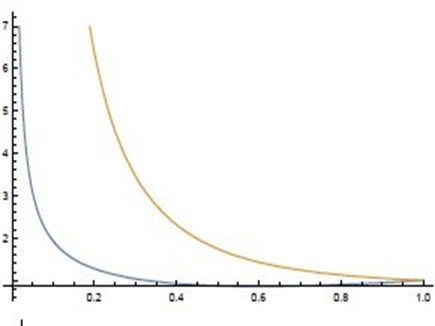
Figure 1 Hubble parameter H(x) (yellow curve) and the expansion velocity $\dot{R}(x)$ (blue curve) as functions of the normalized Hubble scale $x=R/R_0$ .

Going back to the expected recombination point at $R_r=R_0/1000$ one thus learns that the Hubble parameter $H_r=H(R_r)$ for this time is given by:

$H_r=H_0\cdot \sqrt{0.27{(1000)}^{-3}+0.01{(1000)}^{-4}+0.72]}\simeq 0.84H_0$

or expressing the surprising fact that at the expected recombination time $t=t_r$ the photon field does contribute the utmost to the Hubble parameter and amounts at that time $t=t_r$ to a value: $H_r\simeq 0.84H_0$ .

Taking as our basis such a "coasting universe" which prevails for the case of ${\rho }_{\Lambda }\sim R^{-2}$  (${\varrho }_{\Lambda }$  denoting the mass density equivalent of the vacuum energy, R denoting the scale of the universe,⁴ and taking the period when the vacuum energy in the later phases of cosmic expansion unavoidably becomes the dominant ingredient of the cosmic mass density ${\rho }_{\Lambda }\gg {\rho }_b,{\rho }_d,{\rho }_v$ (indices $b,d,v$ standing for baryons, dark matter, and photons, respectively), then one unavoidably finds:

$\dot{R}=\frac{dR}{dt}=const$   (1)

which in fact because $\ddot{R}=0$ of necessarily implies: a "coasting expansion" of the universe! Then consequently a Hubble parameter must be expected that falls off with the cosmic scale R like:

$H(R)=\frac{R}{R}=H_0\cdot (\frac{R_0}{R})$   (2)

meaning that the Hubble parameter $H(R)$ in case of a coasting cosmic expansion permanently decreases like $H\sim R^{-1}$ , and consequently the inverse of it, $H^{-1}$ , i.e. the expansion time period ${\tau }_{ex}=1/H(R)$ of cosmic matter, permanently grows proportional to R!

Structure formation in the cosmic gas

As discussed in Fahr and Zönnchen⁹ in a homogeneous expanding cosmic gas cosmic matter structures can form due to selfgravitational interactions in density perturbations of this cosmic gas. These self-generating structures are persistent phenomena of cosmic sound waves, however, when selfgravity of the oscillatory matter is included. The typical dispersion relation for such self-gravitating, accoustic waves is given in the following form:¹⁰

${\omega }^2(k)=v_s^2{k}^2-4\pi G{\rho }_r$

with as the wave frequency, $k=2\pi /\lambda$ as the wave vector and wave length λ, and $v_s$ as the effective, local sound velocity at recombination era. G is Newton‘s gravitational constant, and ${\rho }_r$ is the actual local matter density at the recombination time $t=t_r$ .

As evident from the above dispersion relation, there exists a critrical wave number $k_c$ with

$k_c=\sqrt{\frac{4\pi G{\rho }_r}{v_s^2}}$

and the property that all waves with wave numbers $k\le k_c$ lead to unstable, standing waves with imaginary values for associated frequencies $\omega$ , i.e. with growing wave amplitudes and hence ongoing of structure formation.

From that fact one can conclude that the characteristic wavelengths of standing wave structures at the recombination epoch are given by:

${\lambda }_c=\frac{2\pi }{k_c}=\frac{2\pi }{\sqrt{\frac{4\pi G{\rho }_r}{v_s^2}}}=\sqrt{\frac{\pi v_s^2}{G{\rho }_r}}$

Calculating the value of ${\lambda }_c$ one obtains with $v_s=\sqrt{\gamma P_r/{\rho }_r}$ and $\gamma =5/3$ , $P_r=n_{r}K{T}_r$ and $T_r$ denoting pressure and temperature of the cosmic H-gas:

${\lambda }_c=\sqrt{\frac{\pi \gamma P_r}{G{\rho }_r^2}}=\sqrt{\frac{\pi \gamma (n_{r}K{T}_r)}{G{\rho }_r^2}}=\sqrt{\frac{\pi \gamma (K{T}_r)}{mG{\rho }_r}}=2.3\sqrt{\frac{K{T}_r}{mG{\rho }_r}}$

The temperature at the recombination era is expected to be about 3000K, and due to the redshift cooling of the present CMB (3K -radiation) one obtains the redshift relation: $(1+z)=(R_0/R_r)\simeq 1000$ . This means that the present cosmic density of the universe ${\rho }_0={10}^{-31}g/c{m}^3$ should have been larger at the recombination era by a factor ${(1000)}^3$ yielding an actual value at $t=t_r$ of ${\rho }_r={10}^{-22}g/c{m}^3$ . This argumentation is based on the assumption that cosmic photons are subject to redshifts which are due to the expansion of the universe. If this cosmic mainstream basis is questioned, then, as we shall show at the end, this would change all of our above conclusions.

The baryon gas temperature $T_r$ , solely due to the influence of the Hubble drift at the recombination era, should develop according to a linear approach for $0.1\ge H_r(t-t_r)$ by:¹¹

$T{}_H(t)=\frac{T{}_{Hr}}{{(1-H_r(t-t_r))}^2}$

and the density is given by :

${\rho }_H(t)={\rho }_r\cdot {(\frac{R(t_r)}{R(t)})}^3$

Covering a time period $\Delta t$ after the recombination point $t-t_r$ , over which the Hubble parameter $H=H_r$ can be considered as constant, permits then to write

$R(t)=R(t_r)\exp [H_r(t-t_r)]$

and consequently yielding the following density as function of time:

${\rho }_H(t)={\rho }_r\cdot {(\frac{R(t_r)}{R(t_r)\exp [H_r(t-t_r)})}^3={\rho }_r\exp [-3H_r(t-t_r)]$

The critical mass $M_c$ of a collapse-critical gas package is then given by:

$M_c=\frac{4\pi }{3}{\lambda }_c^3{\rho }_H=\frac{4\pi }{3}{2.3}^3{(\frac{K{T}_H}{mG{\rho }_H})}^{3/2}{\rho }_H=541.3\cdot {(\frac{K{T}_H}{mG})}^{3/2}{\rho }_H{}^{-1/2}$

If now one introduces the above expressions for $T_H(t)$ and ${\rho }_H(t)$ as functions of t, one then can see the marginally possible, selfgravitational collapse mass $M_c=M_c(t)$ as function of the cosmic time after the recombination point as given by:

$M_c(t)=\frac{4\pi }{3}{\lambda }_c^3(t){\rho }_H(t)=[51.3\cdot {(\frac{K{T}_{H,r}}{mG})}^{3/2}{\rho }_{H,r}{}^{-1/2}]\frac{\exp [(3/2)H_r(t-t_r)]}{{(1-H_r(t-t_r))}^3}=M_{c0}\cdot \mu (t)$

The above expression $\mu (t)$ describing the growth factor of the mass condensate in time is shown in Figure 2.  The three curves represent solutions for three Hubble parameters namely $H_0=H_{today}=70km/s/Mpc;H_1=2H_0$ ; and $H_2=4H_0$ . One can see that the critical mass substantially increases and also reaches an expected magnitude of ${10}^6$ , meaning that masses of the order of $M_c>{10}^{11}{M}_{\odot }$ , i.e. solar masses, within a time of several Billions of years are possible, however, it must be realized that the results of Figure 2 are based on the assumption that within the considered time the actual Hubble parameter is not varying, but keeps a fixed value of $H=H_0;2H_0;4H_0$ .

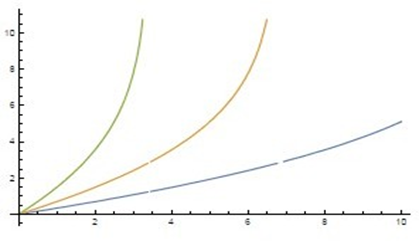
Figure 2 The mass growth factor μ(t) as function of cosmic time in Megayears in a linear approach with H = 1,2,4 H₀.

The above expression shows that possible critical masses $M_c(t)$ are growing with cosmic time t, however, one should keep in mind, to produce elementary cosmic cornerstones like galaxies, one would need a growth factor of about ${10}^6$ . Furthermore there exists a severe limitation for this mass growth given through a comparison between gravitational free-fall times ${\tau }_{ff}$ and expansion times ${\tau }_{ex}$ . The time ${\tau }_{ff}$ is the time it takes to condense the gravitationally unstable mass $M_c(t)$ to a stable structure by its free-fall in the genuine gravitational field, without the pressure action taken into account, and is given by:

${\tau }_{ff}=\frac{1}{\sqrt{4\pi G{\rho }_r}}$

The expansion time ${\tau }_{ex}$ is the typical time needed to expand the mass $M_c(t)$ with the ongoing Hubble expansion to infinity or say: back to the whole universe!, and it is simply given by:

${\tau }_{ex}=\frac{R}{\dot{R}}=\frac{1}{H_r}$

The critical mass can only survive as a cosmic structure, as long as ${\tau }_{ff}$ is smaller than ${\tau }_{ex}$ , meaning that one should numerically have the following relation fulfilled:

$\frac{1}{\sqrt{4\pi G{\rho }_r}}\le \frac{1}{H_r}$

Creation of solar-type collapse centers in a coastingly expanding universe

We shall ask now under which conditions stars like our Sun with masses of $M\sim M_{°}$  can have formed over the epochs of cosmic expansion. This addresses the question whether or not "solar systems" (i.e. planetary systems with a central mass $M=1\cdot M_{°}$ like our Sun) over the cosmic epochs have had different orbital parameters and consequently might have looked different over the cosmic eons. We start from a specific cosmic expansion state characterized by the actual cosmic scale $R(t_0)=R_0$ and the actually prevailing homogeneous cosmic mass density $\varrho (t_0)=\varrho (R_0)={\varrho }_0$  of this epoch.

Let us assume that in this cosmic phase by a locally induced gravitational collapse instability a mass center with a central mass M, just equal to one solar mass $M_{\circ }$ , is formed from all the matter originally uniformly distributed inside the mass-generating source vacuole with a linear dimension $D=D(R)$ , obtained by the following request:

$\frac{4\pi }{3}D{(R)}^3\varrho (R)=\frac{4\pi }{3}D{(R)}^3\varrho (R_0){(\frac{R_0}{R})}^3=M_{\circ }$

This makes evident that the actual linear dimension $D=D(R)$ forming one solar mass unit $M=M_{\circ }$ in the expanding universe is given by:

$D_{\circ }(R)=R\cdot \frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{\varrho }_0}{]}^{1/3}$

expressing the fact that the characteristic solar mass-vacuole with a linear dimension $D_{\circ }(R)$ is just growing proportional to the cosmic scale R of the universe. Hereby it has tacitly been assumed that the universe has a Euclidean geometry with a curvature parameter of $k=0$ .

As motivated in the beginning of this article, we now assume to have a universe with a "coasting expansion" , i.e. with the property that the Hubble constant is given by $H^c(R)=\dot{R}/R=H_0^c\cdot (R_0/R)$ . Then producing via collapse a mass unit of one solar mass $M_{\circ }$ in the center of the sphere with radius $D(R)$ might mean that any massive object at the periphery of the originating vacuole now is attracted in Newton‘s sense by the gravitational field of the central mass $M_{\circ }$ , but at the same time with respect to this mass center it is subject to the differential Hubble drift $v_H=D(R)\cdot H^c(R)$ due to the coasting expansion dynamics. This differential Hubble drift with respect to the mass center supplies the necessary kinetic energy of the peripheral object for its orbital motion around the central mass $M_{\circ }$ .

Looking now both for the specific kinetic energy $E_{kin}$ of this object with respect to the mass center, and for the specific gravitational binding energy $E_{bind}$ of this object with respect to the central mass $M_{\circ }$ one finds:

$E_{kin}=\frac{1}{2}{[D(R)\cdot H^c(R)]}^2$

and:

$E_{bind}=\frac{G{M}_{\circ }}{D(R)}$

where G denotes Newton‘s gravitational constant. Considering the ratio of $\in =E_{kin}/E_{bind}$ kinetic over binding energy of such a "Keplerian" object would then lead to the following expression:

$\in (R)=\frac{\frac{1}{2}{[D(R)\cdot H^c(R)]}^2}{\frac{G{M}_{\circ }}{D(R)}}=\frac{D{(R)}^3{H}^c{(R)}^2}{2G{M}_{\circ }}=\frac{R\cdot \frac{H_o^{c2}}{\frac{4\pi }{3}{R}_0{\varrho }_0}]}{2G}$

This shows that the ratio $\in =\in (R)$ linearly grows with the scale R of the universe which means that the actually arising Kepler problem: "motion of a planet around its sun" all the time in the universe would change its character with the cosmic scale R, in the sense that the appearing Kepler object has higher and higher kinetic energy, while in contrast a bound system can only exist for $\in (R)\le 1$ . This is unavoidable, unless G is assumed to vary proportional to R as discussed in Fahr and Heyl.⁵ In fact for $G(R)=G_0\cdot (R/R_0)$ permanently during the cosmic evolution the same "Kepler"-problem then would arise.

Without a variable G this, however, means that the ratio $\in (R)$ of kinetic over binding energy of the Kepler object is permanently increasing with the increase of the scale of the universe R. In order, however, to have a bound Kepler object, one thus should have $\in \le {\in }_c\le 1,$ which never after achieving a critical scale $R_c$ of the universe will be realizable anymore. Hereby this critical scale $R_c$ is given by

$\begin{array}{l}{R}_c=\frac{2G}{[\frac{H_0^2}{\frac{4\pi }{3}{R}_0{\varrho }_0}]}\\ R\\ \tau =2\pi \sqrt{\frac{D(R)}{g(R)}}=2\pi \sqrt{\frac{D^3(R)}{G{M}_{\circ }}}=2\pi \sqrt{\frac{R^3}{G{M}_{\circ }}[\frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{\varrho }_0}]}\\ {\tau }^2\sim R^3\\ {\tau }^2=2\pi \frac{R^3}{G{M}_{\circ }}[\frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{\varrho }_0}]\\ R\end{array}$

meaning that bound planetary systems with a central mass of $M=1M_{\circ }$ will after that cosmic time $t_c=t(R_c)$ never anymore newly appear during the ongoing expansion of the universe.

This would have the interesting consequence that the "Kepler pendulum" (with the specific acceleration $g(R)=G\cdot M_{\circ }/D^2(R)$  at a distance $D(R)$ from a solar mass object with $M=1$ would act as "a cosmic clock" with a "cosmic oscillation/revolution period of:

$\tau (R)=2\pi \sqrt{L(R)/g(R)}=2\pi \sqrt{D(R)/g(R)}=2\pi \sqrt{D^3(R)/G{M}_{\circ }}=2\pi \sqrt{R^3[\frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{Q}_0}]/G{M}_{\circ }}=2\pi R\sqrt{\frac{R}{G{M}_{\circ }}}\sqrt{\frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{Q}_0}}$

As already mentioned in Fahr and Heyl⁵ again this period would change into a "linear" cosmic clock $\tau (R)\sim R$  when one could assume a scale variable Newton parameter as: $G=G(R)=G_0\cdot (R/R_0)$ .

The more interesting point in this context, however, is that the above derived ratio $\in (R)$ would under this latter assumption in fact be! a cosmologic constant, i.e.:

$\in (r)={\in }_0=\frac{R_0\cdot \frac{H_0^2}{\frac{4\pi }{3}{R}_0{\varrho }_0}}{2G_0}$

if the Newton gravitational coupling coefficient seen over the cosmic eons would not be a constant, but instead would scale with R according to the formula $G=G(R)=G_0\cdot (R/R_0)$ !

This anyway becomes manifest, also without the assumption of the scale variable G, when writing the Kepler pendulum period in the form (taking $D(R)$ as the length of the pendulum, and $g(R)$ as the gravitational acceleration of the central Sun):

$\tau =2\pi \sqrt{\frac{D(R)}{g(R)}}=2\pi \sqrt{\frac{D^3(R)}{G{M}_{\circ }}}=2\pi \sqrt{\frac{R^3}{G{M}_{\circ }}[\frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{\varrho }_0}]}$

and seeing that Kepler‘s third law (i.e. ${\tau }^2\sim R^3$ , $D(R)$ taken as the main axis of the planetary ellipse) would come out quite naturally from the above:

${\tau }^2=2\pi \frac{R^3}{G{M}_{\circ }}[\frac{M_{\circ }}{\frac{4\pi }{3}{R}_0^3{\varrho }_0}]$

So there are obviously two options immaginable: Either under variable G-conditions, like those discussed above, planetary systems can be produced at all cosmic times with the same character as at Newton‘s times,  - or without variable G-conditions the Kepler problem is specific for all cosmic evolution periods and it even exists a critical cosmic scale $R=R_c$ after passing the latter no planetary systems can be built and be expected as arising at all anymore.

In addition assuming that the planetary object at the periphery of the solar mass vacuole starts orbiting the central mass on a circular orbit (i.e. before $R=R_c$ is reached!), then at each of its orbital positions with an orbital velocity the centripetal force equals the gravitational attraction force of the central mass and thus it is required that:

$\frac{v^2}{R}=\frac{G{M}_{\circ }}{R^2}$

meaning that the kinetic energy of the object ${\in }_{kin}=(1/2)m{v}^2$ equals just half the binding energy ${\in }_{kin}=(1/2){\in }_{bind}=(1/2)mG{M}_{\circ }/R$ . This also again leads to Kepler‘s third law concerning the dependence of orbital periods and the main ellipse axis R of the orbit:

${\tau }^2=(\frac{2\pi R}{v})=4{\pi }^2\frac{R^3}{G{M}_{\circ }}$

In constrast to the case given in a static universe¹⁰ processes of structure formation evidently run very different in an expanding universe. This is because then structure formation definitely will depend on the specific form of the prevailing cosmic expansion (e.g. decelerated, accelerated or coasting expansion etc.,).^12-14 To explain the SN-1a luminosities as function of redshifts Perlmutter et al.,² Schmidt et al.,¹ or Riess et al.³ have prefered as basis an accelerated expansion of the universe connected with the action of a constant vacuum energy density. Such a constant vacuum energy is as yet a physically non-understood quantity and is problematic from its physical nature and action.^15-19 There are, however, more recent attempts by Casado²⁰ and Casado and Jou²¹ showing that a "coasting", non-accelerated universe can equally well explain these supernovae luminosities. If in fact vacuum pressure and vacuum energy play a cosmologic role, and if it must be assumed that the universe expands under the thermodynamic and gravodynamic action of vacuum pressure, then as shown by Fahr²² the unavoidable consequence is a "coasting expansion" of the universe with $R=dR/dt=const.,$ R denoting the scale of the universe.

As we do show in this article under the conditions of a coasting, instead of an accelerated, expansion of the universe the origin of new solar-type systems is possible all the time after the cosmic matter recombination, while under the condition of an accelerated expanion of the universe new solar systems cannot be built up after some critical cosmci time period. This could perhaps be a criterion to exclude the possibility of universes with an accelerated Hubble expansion.

None.

None.

None.

1. Schmidt BP. The High-Z Supernova Search: Measuring Cosmic Deceleration and Global Curvature of the Universe Using Type IA Supernovae. Astrophys J. 1998;507(1):46.
2. Perlmutter S, Aldering G, Goldhabe G, et al. The supernova cosmology project: Measurement of Omega and Lambda from 42 high-redshift supernovae. Astrophys J. 1999;517:565–586.
3. Riess AG. Observational evidence for an accelerating universe and a cosmological constant. Astron J. 1998;116(3):1009.
4. Fahr HJ. How much could gravitational binding energy act as hidden cosmic vacuum energy?, Advances Theoret. Computational Physics. 2022;5(2):449–457.
5. Fahr HJ, Heyl M. Evolution of cosmic structures in the expanding universe: Could not one have known it all before? Advances Theoret & Computational Physics. 2022;5(3):524–528.
6. Bennett CL, Hill RS, Hinshaw G. First year of Wilkinson Microwave Anisotropy emission. Astrophys J Supplement. 2003;148(1):97–117.
7. Goenner HFM. Einführung in die Spezielle und Allgemeine Relativitäststheorie, Spektrum Akademischer Verlag, Heidelberg. 1996.
8. Fahr HJ, Heyl M. Structure formation after the era of cosmic recombination. Advances Theoret & Computational Physics. 2021;4(3):253–258.
9. Fahr HJ, Zoennchen J. The writing on the cosmic wall: Is there a straightforward explanation of the cosmic microwave bachground. Annalen der Physik. 2009;18(10-11):699–721.
10. Jeans J Phil. Transactions Royal Society, 199A, 42, 1902, or: Astronomy and Cosmogony, Cambridge University Press, 1929 (Reprinted by Dover Publications, INC, New York, 1940).
11. Fahr HJ. The baryon distribution function in the expanding universe after the recombination era. Phys  Astron Internat Journal. 2021b;5(2):37–41.
12. Kolb EW. A coasting cosmology. Astrophys J. 1989;344:543.
13. Kragh HS. Cosmology and Controversy, Princeton University, Princeton, NJ, 1996.
14. Perlmutter S. Supernovae, Dark energy, and the accelerating universe. Physics Today. 2003;53–60.
15. Einstein A. Kosmologische Betrachtungen zur Allgemeinen Relativitätstheorie, Sitzungsberichte der K.P.Akademie der Wissenschaften. Phys Math Klasse. 1917;142–152.
16. Peebles PJE, Ratra B. The cosmological constant and dark energy. Rev Modern Physcs. 2003;75:559–599.
17. Fahr HJ, Willerding E. Entstehung von Sonnensystemen: Eine Einführung in das Problem der Planetenentstehung". Spektrum Akademischer Verlag, Heidelberg/Berlin. 1998.
18. Kragh HS, Overduin JM. The weight of the vacuum. Springer Briefs in Physics. 2014.
19. Fahr HJ, Heyl M. The thermodynamics of a gravitating vacuum. Astron Nachr/AN. 2014;999(88):789–793.
20. Cassado J, Jou D. Steady flow cosmological models. Astrophys Space Sci. 2013;344(2):513.
21. Cassado J. Linear expansion models versus standard cosmologies; a critical and historical overview. Astrophys Space Sci. 2020;365:16.
22. Fahr HJ, Heyl M. A universe with a constant expansion rate. Physics & Astronomy Internat J. 2020;4(4): 156–163.