In this paper, we derive a specific kinetic transport equation which as a partial differential equation describes the distribution function of cosmic H-gas (i.e. hydrogen atoms). We can infact solve this transport equation and find the gas distribution function as function f(v,t) of the particle velocity v and of the cosmic time t, with the surprising result that the effective temperature of these cosmic particles is not decreasing, but increasing with cosmic time. At the end of the cosmic recombination era, about 400000 years after the Big-Bang, electrons and protons are thought to recombine to neutral cosmic H-atoms. The question poses itself, what happens to this hydrogen (baryon) gas in thermodynamic terms, when it is exposed to the cosmic expansion dynamics of a Robertson-Walker Hubble universe. The result presented here is explained as due to the Hubble-induced velocity drift of the particles in velocity space.

Keywords: Hubble universe, cosmic expansion, hydrogen gas, kinetic transport equation

We start our theoretical considerations from the broadly accepted assumption of modern cosmology, that during the collision-dominated phase of the cosmic evolution, just before the time of matter recombination, matter and radiation in the universe, due to frequent energy exchange processes, are in complete thermodynamic equilibrium. That implies the belief that matter and radiation temperatures at this phase of cosmic evolution are identical, i.e. $T_m=T_s=T_0$ . But in the following cosmic recombination era this equilibrium will certainly experience perturbations as had already been emphasized earlier in a paper by Fahr.¹

The following part of the paper shall demonstrate that, even if a Maxwellian distribution would have prevailed at the entrance to the collision-free cosmic expansion phase, it would not continue to exist for later times. After the recombination phase when electrons and protons recombine to H-atoms, and photons start propagating through cosmic space practically without further interaction with matter, the thermodynamic contact between matter and radiation at the times there after is stopped. For this reason the initial Maxwellian atom distribution function does not persist in an expanding universe over times of the ongoing collision-free expansion.

We consider a collision-free particle population in an expanding, spatially symmetric Robertson-Walker universe (i.e. the so-called RW-Friedman-Lematre universe, see e.g^2–4 Under these guide lines it is clear that due to the cosmological principle or the requirement of spatial homogeneity, the velocity distribution function $f\left(v,t\right)$  of the cosmic particles must be isotropic in velocity space v and independent on the local cosmic place x. Thus $f\left(v,t\right)$  must be of the following general form

$f\left(v,t\right)=n\left(t\right)\cdot \overline{f}\left(v,t\right)$   (1)

where $n\left(t\right)$  denotes the time-variable, cosmic density, only depending on the worldtime t, and $\overline{f}\left(v,t\right)$  is the normalized, time-dependent, isotropic velocity distribution function with the time-independent property

:$4\pi {{\displaystyle \int }}^{\text{}}\overline{f}(v,t)v^{2}dv=1$ . If we now for cosmic particles respect the fact that particles moving freely with their velocity v into the direction $\overrightarrow{v}$  over a distance l , at their new place have to be incorporated into the actual cosmic distribution there, despite the differential Hubble flow and the explicit time-dependence of $f\left(v,t\right)$ , then a locally prevailing distribution function $f\left(\text{'}v\text{`},t\right)\text{'}$  must exist there ensuring that the two associated functions $f\left(\text{'}v\text{`},t\right)\text{'}$  and $f\left(v,t\right)$  are related to each other in an unequivocal, Liouville-conform way,^5–7 simply to guarantee the particle conservation in the universe. As has been shown recently in a lengthy derivation by Fahr⁸ this connection is expressed by the following relation:

$f^{\text{'}}(v^{\text{'}},t^{\text{'}})d^{3}v\text{`}{d}^{3}x\text{`}=f\left(v,t\right)d^{3}v{d}^{3}x$   (2)

When arriving at the place x these particles, after passage over a distance l are incorporated into a particle population which has as a bulk a relative Hubble drift with respect to the origin of the particle given by $v_H=l\cdot H$ , co-aligned with $\overrightarrow{v}$ . Here $H=\dot{R}/R$  denotes the Hubble parameter and characterizes the homologous, dynamic expansion of the universe. Thus the original particle velocity v registered at the new place x is locally tuned down to  $v\text{`}=v-l\cdot H$ . This is because at the present place x, deplaced from the original place x by the increment l, all velocities have to be judged with respect to the new local reference frame (standard of rest) with a differential Hubble drift of ($l\cdot H$ ) with respect to the particles origin. When taking all of that into account, it has been shown Fahr⁸ that one is lead to the following kinetic transport equation for the distribution function $f\left(v,t\right)$ :

$\frac{\partial f}{\partial t}=vH\cdot \left(\frac{\partial f}{\partial v}\right)-H\cdot f$   (3)

The above partial diffreential equation describes the evolution of the function $f\left(v,t\right)$  in cosmic time t and velocity space v. It was shown already by Fahr⁸ that the above kinetic transport equation does not allow for a solution in the form of a separation of variables, i.e. putting $f\left(v,t\right)=f_t\left(t\right)\cdot f_v\left(v\right)$ , but one rather needs a different, non-straightforward method of finding a kinetic solution of this above transport equation, i.e. of Equ.(1). Thus in the following we shall look for such a solution in a more complicated form.

A new access to the kinetic problem

In the aforegoing section we have briefly reviewed the mathematical procedure to describe the physical and thermodynamical behaviour of a cosmic baryon gas, i.e. essentially of the H-atom gas just after the process of recombination of cosmic electrons and protons at and after the recombination phase of cosmic matter roughly about  years after the Big Bang. In Fahr⁸ the relevant kinetic transport equation has been derived given by Equ.(1) for this cosmic situation. This eqution in its original form, however, could not be solved by an associated kinetic distribution function $f\left(v,t\right)$ . Only the velocity moments of this function $f\left(v,t\right)$ , like the density $n\left(t\right)$  and the pressure $P\left(t\right)$ , could be precisely derived as function of the cosmic time t. With this knowledge of the excact form of the kinetic transport equation and the knowledge of the moments $n\left(t\right)$  and $P\left(t\right)$  as functions of cosmic time one could be seduced to now be more ambitious and to find out more about the kinetic situation of the cosmic gas under these conditions just after the recombination era.

The kinetic transport equation

What kind of distribution function $f(v,t>t_0)$  and what kind of temporal change of it should be expected for that period? To answer this question we want to approach the problem here a little bit from an other direction and want to use here a new independent way to access this kinetic problem, namely to use a slightly different kinetic transport equation compared to that used by Fahr⁸ however nevertheless treating the identical cosmophysical situation as already envisioned there. Starting from a kinetic transport equation used by Fahr⁹ for a plasma physical scenario which, however, for the purposes here is directly transferable, since only of importance in both cases are the two terms for a temporal derivative of $f\left(v,t\right)$  and for the particle redistribution in velocity space, in our case here due to the Hubble-induced velocity space drift ${\dot{v}}_H={\dot{v}}_H\left(v\right)$  of the particles. With these two terms the kinetic transport equation would then attain the following, surprisingly simple form describing the temporal change of the distribution function as due to the spherical Hubble drift of the particles on spherical shells in velocity space:

$\frac{\partial f\left(v,t\right)}{\partial t}=\frac{1}{v^2}\frac{\partial }{\partial v}\left[v^2{\dot{v}}_{H}f\left(v,t\right)\right]$

where the term on the left side denotes the explicit temporal change of the distribution function $f\left(v,t\right)$  and the term on the right side describes the temporal change of the distribution function $f\left(v,t\right)$  under the Hubble-induced velocity drift migration ${\dot{v}}_H=-v\cdot H$ , quite analogous to the velocity space drift which was formulated as due to wave-particle-induced velocity diffusion for a different, but analogously operating plasma-physical scenario in Farh¹⁰ In this case here, this drift is connected with the fact that particles which move with a velocity v into the direction $\overrightarrow{v}$  within a time increment $dt$  suffer a velocity change ${\dot{v}}_H=dv/dt=-v\cdot H$  with respect to the new reference place which is reached by the particle at time $t\text{`}=t_0+dt$ . This consequently then allows to write the above kinetic transport equation after introduction of the normalized distribution in the form $f\left(t,v\right)=n\left(t\right)\cdot \overline{f}\left(v,t\right)$  by use of the explicit time-dependence of the density $n=n\left(t\right)$  in the following form:

$\frac{\partial }{\partial t}\left[n\left(t\right)\cdot \overline{f}\left(v,t\right)\right]=-\frac{1}{v^2}\frac{\partial }{\partial v}\left[v^2\left(vH\right)f\left(v,t\right)\right]=-\frac{H}{v^2}n\left(t\right)\frac{\partial }{\partial v}\left[v^3\overline{f}\left(t,v\right)\right]$

which can then be developed into the following form:

$\overline{f}\left(v,t\right)\frac{\partial n}{\partial t}+n\left(t\right)\frac{\partial }{\partial t}\overline{f}\left(v,t\right)=-\frac{H}{v^2}n\left(t\right)\frac{\partial }{\partial v}\left[v^3\overline{f}\left(v,t\right)\right]=-\frac{H}{v^2}n\left(t\right)\left[3v^2\overline{f}\left(v,t\right)+v^3\frac{\partial }{\partial v}\overline{f}\left(v,t\right)\right]$

and further arranges into :

$\frac{1}{n\left(t\right)}\frac{\partial n}{\partial t}+\frac{1}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial t}\overline{f}\left(v,t\right)=-H\cdot 3+\frac{v}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial v}\overline{f}\left(v,t\right)]$

We now furthermore must take into account that the normalized distribution $\overline{f}\left(v,t\right)$  also, however, is indirectly dependent on cosmic time t, because of the action of the Hubble-induced temporal velocity change which particles experience while moving to a new reference place. This implies that also $\overline{f}\left(v,t\right)$ , though being a normalized function, has to be indirectly differentiated with respect to t in the following way:

$\frac{1}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial t}\overline{f}\left(v,t\right)=\frac{1}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial v}\overline{f}\left(v,t\right)\frac{\partial v}{\partial t}=\left[\frac{1}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial v}\overline{f}\left(v,t\right)\right]\left(-vH\right)$

Putting these things together with the upper differential equation we then obtain the following equation:

$\frac{1}{n\left(t\right)}\frac{\partial n}{\partial t}+\left[\frac{1}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial v}\overline{f}\left(v,t\right)\left]\left(-vH\right)=\right[-3H-\frac{Hv}{\overline{f}\left(v,t\right)}\frac{\partial }{\partial v}\overline{f}\left(v,t\right)\right]$

consequently leading to the surprisingly simple equation:

$\frac{1}{n\left(t\right)}\frac{\partial n}{\partial t}=-3H$

and leading to the following solution

$n\left(t\right)=n_0\exp \left[-3H\left(t-t_0\right)\right]$

The Baryon distribution function

In order to now solve for the rest of the remaining kinetics, we have to find the solution for the function $\overline{f}\left(v,t\right)$ . In view of the fact that at time $t\le t_0$  (before the recombination) matter and radiation are expected to be in thermodynamical equilibrium, one may start with the assumption that $\overline{f}\left(v,t_0\right)$  has a Maxwellian shape, i.e. at time $t=t_0$  one can expect the following function:

$\overline{f}\left(v,t_0\right)=\frac{1}{{\pi }^{3/2}{(K{T}_0/m)}^{3/2}}\exp \left[-\frac{m{v}^2}{K{T}_0}\right]$

where $T_0$  is the Maxwellian particle temperature at time $t_0$ , and $\overline{f}\left(v,t_0\right)$  in fact fullfills the normalization requirement as all Maxwellian do:

$4\pi {{\displaystyle \int }}^{\text{}}\overline{f}\left(v,t_0\right)v^{2}dv=4\pi {{\displaystyle \int }}^{\text{}}\frac{1}{{\pi }^{3/2}{(K{T}_0/m)}^{3/2}}\exp \left[-\frac{m{v}^2}{K{T}_0}\right]v^{2}dv=1$

To look for times $t\ge t_0$  we now have to pay attention to the dynamical action of the Hubble drift $\dot{v}=-v\cdot H$  suffered by all particles and therefore may guess the following solution:

$\overline{f}\left(v,t\ge t_0\right)=\frac{1}{{\pi }^{3/2}{(K{T}_0/m)}^{3/2}}\exp \left[-\frac{m{(v-vH\left(t-t_0\right))}^2}{K{T}_0}\right]=\frac{1}{{\pi }^{3/2}{(K{T}_0/m)}^{3/2}}\exp [-\frac{m{v}^2}{K{T}_0}\left(1-H\left(t-t_0\right){)}^2\right]$

which for first glance looks reasonable, however, when reminding that we have required $\overline{f}\left(v,t\right)$  to be a normalized function at all times with the property $4\pi {{\displaystyle \int }}^{\text{}}\overline{f}\left(v,t\right)v^{2}dv=1$ , we shall have to check now whether the above representation does fulfill this request at all times t, and find,

$4\pi {{\displaystyle \int }}^{\text{}}\overline{f}\left(v,t\ge t_0\right)v^{2}dv=\frac{4\pi }{{\pi }^{3/2}{(K{T}_0/m)}^{3/2}}{{\displaystyle \int }}^{\text{}}\exp [-\frac{m{v}^2}{K{T}_0}\left(1-H\left(t-t_0\right){)}^2\right]v^{2}dv\cdot {(1-H\left(t-t_0\right))}^3$

which at a first glance does perhaps not make it evident that the normalization condition is fulfilled, but one can easily arrange things to make that evident, when introducing a new time-dependent Maxwellian temperature $T\left(t\right)$  given by:

$T\left(t\right)=T_0\cdot {(1-H\left(t-t_0\right))}^{-2}$

One then can convince oneself that the normalization is fulfilled , because then the wanted normalized distribution function would lead to:

$1=4\pi {{\displaystyle \int }}^{\text{}}\overline{f}\left(v,t\ge t_0\right)v^{2}dv=\frac{4\pi }{{\pi }^{3/2}{(KT\left(t\right)/m)}^{3/2}}{{\displaystyle \int }}^{\text{}}\exp \left[-\frac{m{v}^2}{KT\left(t\right)}\right]v^{2}dv$

Hence when putting things together we arrive at the final result for the wanted distribution function given in the following form:

$f\left(v,t\right)=n\left(t\right)\cdot \overline{f}\left(v,t\ge t_0\right)=n_0\exp \left[-3H\left(t-t_0\right)\right]\cdot \frac{1}{{\pi }^{3/2}{(KT\left(t\right)/m)}^{3/2}}\exp \left[-\frac{m{v}^2}{KT\left(t\right)}\right]$

or in a more concise form given by:

$f\left(v,t\right)=n_0\exp \left[-3H\left(t-t_0\right)\right]\cdot \frac{{(1-H\left(t-t_0\right))}^3}{{\pi }^{3/2}{(K{T}_0/m)}^{3/2}}\exp [-\frac{m{v}^2}{K{T}_0}\left(1-H\left(t-t_0\right){)}^2\right]$

Introduction of the mean thermal velocity $v_0$  at $t=t_0$  by: $v_0^2=K{T}_0/m$   then finally with $x=v/v_0$  leads to the following more usefull form:

$f\left(v,t\right)=n_0\exp \left[-3H\left(t-t_0\right)\right]\cdot \frac{{(1-H\left(t-t_0\right))}^3}{{\pi }^{3/2}{v}_o^3}\exp [-x^2\cdot \left(1-H\left(t-t_0\right){)}^2\right]$

In Figures 1 & 2 we show the above distribution function normalized by the density, i.e. $f\left(x,t\right)/n\left(t\right)$ , and the associated differential velocity space density, i.e. $x^{2}f\left(x,t\right)/n\left(t\right)$   as function of the normalized velocity $x=v/v_0$  for different times $t\ge t_0$ .

Figure 1 The baryon probability distribution $f\left(x,t\right)/n\left(t\right)$ is shown as function of the normalized velocity $x=v/v_0$ for times 1, 2, 3, 4 Billion years after the recombination time at $t=t_0$ .

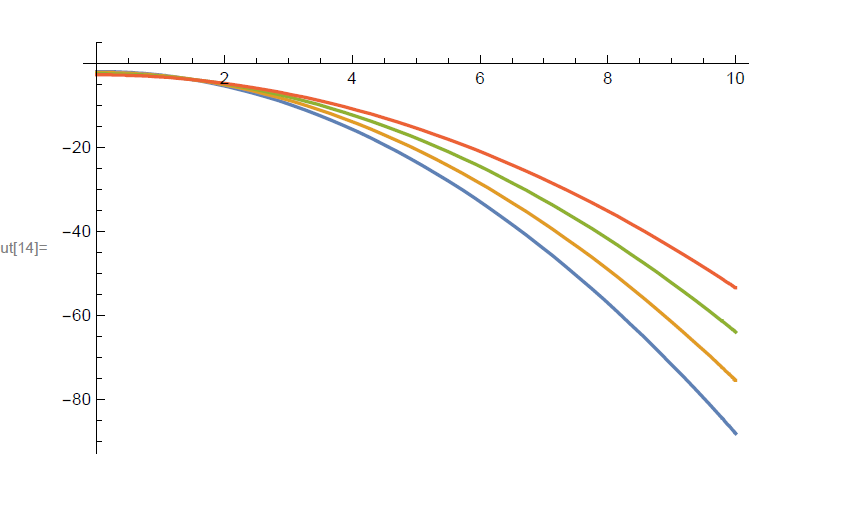
Figure 2 The differential velocity space distribution $x^{2}f\left(x,t\right)/n\left(t\right)$ is shown as function of the normalized velocity $x=v/v_0$ for times of 1, 2, 3, 4 Billion years after the recombination point at $t=t_0$ .

In this paper we have shown that the problem of the gas dynamic behaviour of a homogeneous cosmic baryon gas in an expanding universe can be solved on the basis of a special kinetic transport equation describing the temporal change of the kinetic distribution function $f\left(v,t\right)$  due to the decelerated motions of the particles in velocity space as reaction to the Hubble migration drift which cares for a typical velocity change per time of each particle according to $\dot{v}=-v\cdot H$ . The influence of these particle drifts we have described by a kind of spherical diffusion of the particles through spherical shells in velocity space and could find the solution of the particle distribution function $f\left(v,t\right)$  as function of the velocity v and the cosmic time t (see section above and our Figures 1 & 2. As these figures do show the original Maxwellian with a temperature $T=T_0=4000K$  is changing in the billions of years following the matter recombination at time $t=t_0$  by systematically transporting the particles from higher to lower velocities which, however in such a regularized way that it in fact corresponds to the increase of the accociated, effective temperature of the distribution function by $T\left(t\right)=T_0\cdot {(1-H\left(t-t_0\right))}^{-2}$ . This is shown in Figure 3 by means of the normalized, average kinetic energy $\overline{E}(xzt)=\left(4\pi /{{\rm E}}_0\right)\underset{0}{\overset{x}{{\displaystyle \int }}}m{x}^4\overline{f}\left(x,t\right)dx$  as function of the upper integration border $x=v/v_0$  for different cosmic times of  Billion years after the recombination point at $t=t_0$ .

Figure 3 The average thermal energy, normalized with its value $E_0=K{T}_0$ at $t=t_0$ , i.e. $\left(4\pi /E_0\right)\underset{0}{\overset{x}{{\displaystyle \int }}}m{x}^4\overline{f}\left(x,t\right)dx$ , is shownas function of the upper integration border $x=v/v_0$ at times 1, 2, 3, 4 Billion years after the recombination point at $t=t_0$ .

None.

The authors declare no conflicts of interest.

1. Fahr HJ, Loch R. Photon stigmata from the recombination phase superimposed on the cosmological background radiation. Astron & Astrophys. 1991;246;1–9.
2. Rindler W. Essential relativity special, general and cosmological. Physics. 1977.
3. Tolman R. Relativity Thermodynamics and Cosmology. Dove Publications Inc. New York. 1987.
4. Fahr HJ. Mit oder ohne Urknall das ist hier die Frage?. Springer Spektrum Publ. Berlin-Heidelberg. 2016.
5. Chapman S, Cowling TG. The mathematical theory of non-uniform gases. London. Cambridge University Press. 1952.
6. Cercigniani C. The Boltzmann equation and its applications. New York. Springer Verlag. 1988.
7. Lifshitz E, Pitaevskii L. Physical Kinetics Course of Theoretical Physics. Elsevier Scienec. 1995;10.
8. Fahr HJ. The thermodynamics of cosmic gases in expanding universes based on Vlasow-theoretcial grounds. Adv Theoret Computat Physics. 2021;4(2):129–133.
9. Fahr HJ. Mit oder ohne Urknall das ist hier die Frage? Springer Spektrum Publ. Berlin-Heidelberg. 2016.
10. Fahr HJ. Revisiting the theory of the evolution of pick-up ion distributions: magnetic or adiabatic cooling?. Annales Geophys. 2007;25:2649–2659.