The backlund transformation of the generalized Riccati equation and its applications to the nonlinear KPP equation

doi:10.15406/paij.2017.01.00007

eISSN: 2576-4543

Physics & Astronomy International Journal

Research Article Volume 1 Issue 1

The backlund transformation of the generalized Riccati equation and its applications to the nonlinear KPP equation

Elsayed ME Zayed,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Khaled AE Alurrfi,² Abdul Ghani Al Nowehy³

¹Department of Mathematics, Faculty of Sciences, Zagazig University, Egypt
²Department of Mathematics, Faculty of Arts & Science, Mergib University, Libya
³Department of Mathematics, Faculty of Education and Science, Taiz University, Yemen

Correspondence: Elsayed ME Zayed, Department of Mathematics, Faculty of Sciences, Zagazig University, Zagazig, Egypt

Received: June 17, 2017 | Published: August 30, 2017

Citation: Zayed EME, Alurrfi KAE, Al-Nowehy AG. The backlund transformation of the generalized Riccati equation and its applications to the nonlinear KPP equation. Phys Astron Int J. 2017;1(1):39-47. DOI: 10.15406/paij.2017.01.00007

Download PDF

Abstract

The Bäcklund transformation of the generalized Riccati equation is applied in this article to construct many new exact traveling wave solutions for the nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation. Solutions, trigonometric and rational solutions of this equation are obtained. This transformation is straightforward and concise. It gives much more general results than the well-known results obtaining by other methods. With the aid of Maple, some graphical representations for some results are presented by choosing suitable values of parameters.

Keywords: exact traveling wave solutions, bäcklund transformation of generalized Riccati equation, kolmogorov-petrovskii-piskunov equation, soliton solutions, trigonometric solutions, rational solutions

Mathematics subject classification

35K99, 35P05, 35P99, 35C05

Introduction

The investigation of exact traveling wave solutions to nonlinear PDEs plays an important role in the study of nonlinear physical phenomena. Nonlinear wave phenomena appears in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibers, biology, solid state physics, chemical kinematics, chemical physics and geochemistry. Nonlinear wave phenomena of dispersion, dissipation, diffusion, reaction and convection are very important in nonlinear wave equations. In recent decades, many effective methods have been established to obtain exact solutions of nonlinear PDEs, such as the inverse scattering transform,¹ the Hirota method,² the truncated Painlevé expansion method,³ the Bäcklund transform method,¹^,⁴^,⁵ the exp-function method,⁶^–⁸ the simplest equation method,⁹^,¹⁰ the Weierstrass elliptic function method,¹¹ the Jacobi elliptic function method,¹²^{^–}¹⁴ the tanh-function method,¹⁵^,¹⁶ the $(G^{'} / G)$ expansion method,¹⁷^–²² the modified simple equation method,²³^–²⁶ the Kudryashov method,²⁷^–²⁹ the multiple exp-function algorithm method,³⁰^,³¹ the transformed rational function method,³² the Frobenius decomposition technique,³³ the local fractional variation iteration method,³⁴ the local fractional series expansion method,³⁵ the $(\frac{G^{'}}{G}, \frac{1}{G})$ expansion method,³⁶^–⁴⁰ the generalized Riccati equation mapping method⁴¹^–⁴⁵ and so on.

The objective of this article is to use the Bäcklund transformation of the generalized Riccati equation to construct new exact traveling wave solutions of the following nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation.²²^,²⁶^,⁴⁶

$u_{t} - u_{x x} + μ u^{2} + γ u^{2} + δ u^{3} = 0$ (1.1)

Where $μ, γ, δ$ are real constants. Equation (1.1) includes the Fisher equation, Huxley equation, Burgers-Huxley equation, Chaffee-Infanfe equation and Fitzhugh-Nagumo equation as special cases. Recently, Feng et al.²² have discussed Equation (1.1) using the $(G^{'} / G)$ -expansion method and found its exact solutions, while Zayed et al.²⁶^,⁴⁶ have applied two methods via the modified simple equation method and the Riccati equation method combined with the $(G^{'} / G)$ -expansion method respectively, to Equation (1.1) and determined the exact traveling wave solutions of it.

This paper is organized as follows: In Section 2, the description of the Bäcklund transformation of the generalized Riccati equation is given. In Section 3, we use the given method described in Section 2, to find many new exact traveling wave solutions of the nonlinear KPP equation. In Section 4, physical explanations of some results are presented. In Section 5, some conclusions are obtained.

Description of the bäcklund transformation of the generalized riccati equation

Suppose that we have the following nonlinear PDE:

$F (u, u_{t}, u_{x}, u_{t t}, u_{x x}, ...) = 0,$ (2.1)

Where $F$ is a polynomial in $u (x, t)$ and its partial derivatives, in which the highest order derivatives and the nonlinear terms are involved. In the following, we give the main steps of this method [5]:

Step 1: Using the wave transformation

$u (x, t) = u (ξ), ξ = k x + ω t,$ (2.2)

where $k$ and $ω$ are constants, to reduce Equation (2.1) to the following ODE:

$P (u, u^{'}, u^{″}, ...) = 0,$ (2.3)

where $P$ is a polynomial in $u (ξ)$ and its total derivatives while $^{'} = d / d ξ .$

Step 2: Assume that Equation (2.3) has the formal solution

$u (ξ) = \sum_{i = 0}^{N} a_{i} ψ {(ξ)}^{i},$ (2.4)

where $a_{i}$ are constants to be determined, such that $a_{N} \neq 0$ , while $ψ (ξ)$ comes from the following Bäcklund transformation

$ψ (ξ) = \frac{- r B + A φ (ξ)}{A + B φ (ξ)},$ (2.5)

where $r, A, B$ are constants with $B \neq 0,$ while $φ (ξ)$ satisfies the generalized Riccati equation:

$φ^{'} (ξ) = r + p φ (ξ) + q φ {(ξ)}^{2},$ (2.6)

where $p, q$ are constants, such that $q \neq 0$ .

It is well-known^41-⁴⁵ that Equation (2.6) has many families of solutions as follows:

Family 1: When $p^{2} - 4 q r > 0$ and $p q \neq 0$ or $q r \neq 0$ , we have

$φ_{1} (ξ) = - \frac{1}{2 q} (p + \sqrt{p^{2} - 4 q r} \tanh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ)),$

$φ_{2} (ξ) = - \frac{1}{2 q} (p + \sqrt{p^{2} - 4 q r} \coth (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ)),$

$φ_{3} (ξ) = - \frac{1}{2 q} (p + \sqrt{p^{2} - 4 q r} (\coth (\sqrt{p^{2} - 4 q r} ξ) \pm c s c h (\sqrt{p^{2} - 4 q r} ξ))),$

$φ_{4} (ξ) = - \frac{1}{4 q} (2 p + \sqrt{p^{2} - 4 q r} (\tanh (\frac{\sqrt{p^{2} - 4 q r}}{4} ξ) + \coth (\frac{\sqrt{p^{2} - 4 q r}}{4} ξ))),$

$φ_{5} (ξ) = \frac{1}{2 q} (- p + \frac{\pm \sqrt{(R^{2} + M^{2}) (p^{2} - 4 q r)} - A \sqrt{p^{2} - 4 q r} \cosh (\sqrt{p^{2} - 4 q r} ξ)}{R \sinh (\sqrt{p^{2} - 4 q r} ξ) + M}),$

$φ_{6} (ξ) = \frac{1}{2 q} (- p - \frac{\pm \sqrt{(M^{2} - R^{2}) (p^{2} - 4 q r)} + A \sqrt{p^{2} - 4 q r} \sinh (\sqrt{p^{2} - 4 q r} ξ)}{R \cosh (\sqrt{p^{2} - 4 q r} ξ) + M}),$

Where $R$ and $M$ are nonzero real constants satisfying $M^{2} - R^{2} > 0$ .

$φ_{7} (ξ) = \frac{2 r \cosh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ)}{\sqrt{p^{2} - 4 q r} \sinh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ) - p \cosh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ)},$

$φ_{8} (ξ) = \frac{- 2 r \sinh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ)}{p \sinh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ) - \sqrt{p^{2} - 4 q r} \cosh (\frac{\sqrt{p^{2} - 4 q r}}{2} ξ)},$ $φ_{9} (ξ) = \frac{2 r \sinh (\sqrt{p^{2} - 4 q r} ξ)}{- p \sinh (\sqrt{p^{2} - 4 q r} ξ) + \sqrt{p^{2} - 4 q r} \cosh (\sqrt{p^{2} - 4 q r} ξ) \pm \sqrt{p^{2} - 4 q r}},$ $φ_{10} (ξ) = \frac{4 r \sinh (\frac{1}{4} \sqrt{p^{2} - 4 q r} ξ) \cosh (\frac{1}{4} \sqrt{p^{2} - 4 q r} ξ)}{- 2 p \sinh (\frac{1}{4} \sqrt{p^{2} - 4 q r} ξ) \cosh (\frac{1}{4} \sqrt{p^{2} - 4 q r} ξ) + 2 \sqrt{p^{2} - 4 q r} \cosh^{2} (\frac{1}{4} \sqrt{p^{2} - 4 q r} ξ) - \sqrt{p^{2} - 4 q r}} .$

Family 2: When $p^{2} - 4 q r < 0$ and $p q \neq 0$ or $q r \neq 0$ , we have

$φ_{11} (ξ) = \frac{1}{2 q} (- p + \sqrt{4 q r - p^{2}} \tan (\frac{\sqrt{4 q r - p^{2}}}{2} ξ)),$

$φ_{12} (ξ) = - \frac{1}{2 q} (p + \sqrt{4 q r - p^{2}} \cot (\frac{\sqrt{4 q r - p^{2}}}{2} ξ)),$

$φ_{13} (ξ) = \frac{1}{2 q} (- p + \sqrt{4 q r - p^{2}} (\tan (\sqrt{4 q r - p^{2}} ξ) \pm \sec (\sqrt{4 q r - p^{2}} ξ))),$ $φ_{14} (ξ) = - \frac{1}{2 q} (p + \sqrt{4 q r - p^{2}} (\cot (\sqrt{4 q r - p^{2}} ξ) \pm \csc (\sqrt{4 q r - p^{2}} ξ))),$ $φ_{15} (ξ) = \frac{1}{4 q} (- 2 p + \sqrt{4 q r - p^{2}} (\tan (\frac{\sqrt{4 q r - p^{2}}}{4} ξ) - \cot (\frac{\sqrt{4 q r - p^{2}}}{4} ξ))),$ $φ_{16} (ξ) = \frac{1}{2 q} (- p + \frac{\pm \sqrt{(R^{2} - M^{2}) (4 q r - p^{2})} - A \sqrt{4 q r - p^{2}} \cos (\sqrt{4 q r - p^{2}} ξ)}{R \sin (\sqrt{4 q r - p^{2}} ξ) + M}),$

$φ_{17} (ξ) = \frac{1}{2 q} (- p - \frac{\pm \sqrt{(R^{2} - M^{2}) (4 q r - p^{2})} + A \sqrt{4 q r - p^{2}} \sin (\sqrt{4 q r - p^{2}} ξ)}{R \cos (\sqrt{4 q r - p^{2}} ξ) + M}),$

where $R$ and $M$ are two nonzero real constants satisfying $R^{2} - M^{2} > 0$ .

$φ_{18} (ξ) = \frac{- 2 r \cos (\frac{\sqrt{4 q r - p^{2}}}{2} ξ)}{\sqrt{4 q r - p^{2}} \sin (\frac{\sqrt{4 q r - p^{2}}}{2} ξ) + p \cos (\frac{\sqrt{4 q r - p^{2}}}{2} ξ)},$

$φ_{19} (ξ) = \frac{2 r \sin (\frac{\sqrt{4 q r - p^{2}}}{2} ξ)}{- p \sin (\frac{\sqrt{4 q r - p^{2}}}{2} ξ) + \sqrt{4 q r - p^{2}} \cos (\frac{\sqrt{4 q r - p^{2}}}{2} ξ)},$ $φ_{20} (ξ) = \frac{- 2 r \cos (\sqrt{4 q r - p^{2}} ξ)}{\sqrt{4 q r - p^{2}} \sin (\sqrt{4 q r - p^{2}} ξ) + p \cos (\sqrt{4 q r - p^{2}} ξ) \pm \sqrt{4 q r - p^{2}}} .$ $φ_{21} (ξ) = \frac{2 r \sin (\sqrt{4 q r - p^{2}} ξ)}{- p \sin (\sqrt{4 q r - p^{2}} ξ) + \sqrt{4 q r - p^{2}} \cos (\sqrt{4 q r - p^{2}} ξ) \pm \sqrt{4 q r - p^{2}}},$ $φ_{22} (ξ) = \frac{4 r \sin (\frac{1}{4} \sqrt{4 q r - p^{2}} ξ) \cos (\frac{1}{4} \sqrt{4 q r - p^{2}} ξ)}{- 2 p \sin (\frac{1}{4} \sqrt{4 q r - p^{2}} ξ) \cos (\frac{1}{4} \sqrt{4 q r - p^{2}} ξ) + 2 \sqrt{4 q r - p^{2}} \cos^{2} (\frac{1}{4} \sqrt{4 q r - p^{2}} ξ) - \sqrt{4 q r - p^{2}}} .$

Family 3: When $r = 0$ and $p q \neq 0$ , we have

$φ_{23} (ξ) = \frac{- p d}{q (d + \cosh (p ξ) - \sinh (p ξ))},$

$φ_{24} (ξ) = \frac{- p (\cosh (p ξ) + \sinh (p ξ))}{q (d + \cosh (p ξ) + \sinh (p ξ))},$

where $d$ is an arbitrary constant.

Family 4: When $q \neq 0$ and $r = p = 0$ , we have

$φ_{25} (ξ) = \frac{- 1}{q ξ + c_{1}},$

where $c_{1}$ is an arbitrary constant.

Step 3: We determine the positive integer $N$ in (2.4) by using the homogeneous balance between the highest-order derivatives and the nonlinear terms in Equation (2.3). More precisely we define the degree of $u (ξ)$ as $D [u (ξ)] = N$ which gives rise to the degree of other expressions as follows:

$\begin{matrix} D [\frac{d^{l} u}{d ξ^{l}}] = N + l, \\ D [u^{m} {(\frac{d^{l} u}{d ξ^{l}})}^{s}] = N m + s (l + N) . \end{matrix}$ (2.7)

Therefore, we can get the value of $N$ in (2.4).

Step 4: We substitute (2.4) along with Equations (2.5) and (2.6) into Equation (2.3), collect all the terms with the same powers of $φ^{i} (ξ)$ and set them to zero, we obtain a system of algebraic equations, which can be solved by Maple to get the values of $a_{i}$ , $k$ and $ω$ . Consequently, we obtain the exact traveling wave solutions of Equation (2.1).

An application

In this section, we will apply the method described in Section 2 to find the exact traveling wave solutions of the nonlinear KPP equation (1.1). To this end, we use the wave transformation (2.2) to reduce Equation (1.1) to the following ODE:

$ω u^{'} (ξ) - k^{2} u^{″} (ξ) + μ u (ξ) + γ u^{2} (ξ) + δ u^{3} (ξ) = 0.$ (3.1)

By balancing $u^{″}$ with $u^{3}$ in Equation (3.1), we get $N = 1$ . Consequently, we have the formal solution

$u (ξ) = a_{0} + a_{1} ψ (ξ),$ (3.2)

where $a_{0}, a_{1}$ are constants to be determined, such that $a_{1} \neq 0,$ while $ψ (ξ)$ is given by (2.5).

Now, substituting (3.2) along with Equations (2.5) and (2.6) into (3.1), collecting the coefficients of $φ^{i} (ξ)$ and setting them to zero, we get the following system of algebraic equations:

$φ^{3} : δ A^{3} a_{1}^{3} - 2 A^{3} k^{2} q^{2} a_{1} + p A^{2} B k^{2} q a_{1} + ω A^{2} B q a_{1} + 3 δ A^{2} B a_{0} a_{1}^{2} + γ A^{2} B a_{1}^{2} - 2 r A B^{2} k^{2} q^{2} a_{1} + 3 δ A B^{2} a_{0}^{2} a_{1} + 2 γ A B^{2} a_{0} a_{1} + μ A B^{2} a_{1} + p r B^{3} k^{2} q a_{1} + r ω B^{3} q a_{1} + δ B^{3} a_{0}^{3} + γ B^{3} a_{0}^{2} + μ B^{3} a_{0} = 0,$

$+ 3 δ A B^{2} a_{0}^{2} a_{1} + 2 γ A B^{2} a_{0} a_{1} + μ A B^{2} a_{1} + p r B^{3} k^{2} q a_{1} + r ω B^{3} q a_{1} + δ B^{3} a_{0}^{3} + γ B^{3} a_{0}^{2} + μ B^{3} a_{0} = 0,$

$φ^{2} : 3 δ A^{3} a_{0} a_{1}^{2} - 3 q A^{3} k^{2} p a_{1} + γ A^{3} a_{1}^{2} + q ω A^{3} a_{1} + A^{2} B k^{2} p^{2} a_{1} + 2 q A^{2} B k^{2} r a_{1} + ω A^{2} B p a_{1}$

$- 3 δ A^{2} B r a_{1}^{3} + 6 δ A^{2} B a_{0}^{2} a_{1} + 4 γ A^{2} B a_{0} a_{1} + 2 μ A^{2} B a_{1} - 3 q A B^{2} k^{2} p r a_{1} - 6 δ A B^{2} r a_{0} a_{1}^{2}$

$- 2 γ A B^{2} r a_{1}^{2} + q ω A B^{2} r a_{1} + 3 δ A B^{2} a_{0}^{3} + 3 γ A B^{2} a_{0}^{2} + 3 μ A B^{2} a_{0} + B^{3} k^{2} p^{2} r a_{1}$

$+ 2 q B^{3} k^{2} r^{2} a_{1} + ω B^{3} p r a_{1} - 3 δ B^{3} r a_{0}^{2} a_{1} - 2 γ B^{3} r a_{0} a_{1} - μ B^{3} r a_{1} = 0,$

$φ : ω A^{3} p a_{1} - 2 q A^{3} k^{2} r a_{1} - A^{3} k^{2} p^{2} a_{1} + 3 δ A^{3} a_{0}^{2} a_{1} + 2 γ A^{3} a_{0} a_{1} + μ A^{3} a_{1} + 3 A^{2} B k^{2} p r a_{1}$

$- 6 δ A^{2} B r a_{0} a_{1}^{2} - 2 γ A^{2} B r a_{1}^{2} + ω A^{2} B r a_{1} + 3 δ A^{2} B a_{0}^{3} + 3 γ A^{2} B a_{0}^{2} + 3 μ A^{2} B a_{0} - A B^{2} k^{2} p^{2} r a_{1}$

$- 2 q A B^{2} k^{2} r^{2} a_{1} + ω A B^{2} p r a_{1} + 3 δ A B^{2} r^{2} a_{1}^{3} - 6 δ A B^{2} r a_{0}^{2} a_{1} - 4 γ A B^{2} r a_{0} a_{1} - 2 μ A B^{2} r a_{1}$

$+ 3 B^{3} k^{2} p r^{2} a_{1} + 3 δ B^{3} r^{2} a_{0} a_{1}^{2} + γ B^{3} r^{2} a_{1}^{2} + ω B^{3} r^{2} a_{1} = 0,$

$φ^{0} : ω A^{3} r a_{1} - p A^{3} k^{2} r a_{1} + δ A^{3} a_{0}^{3} + γ A^{3} a_{0}^{2} + μ A^{3} a_{0} + 2 A^{2} B k^{2} r^{2} a_{1} - 3 δ A^{2} B r a_{0}^{2} a_{1} - 2 γ A^{2} B r a_{0} a_{1}$ $- μ A^{2} B r a_{1} - p A B^{2} k^{2} r^{2} a_{1} + 3 δ A B^{2} r^{2} a_{0} a_{1}^{2} + γ A B^{2} r^{2} a_{1}^{2} + ω A B^{2} r^{2} a_{1} + 2 B^{3} k^{2} r^{3} a_{1} - δ B^{3} r^{3} a_{1}^{3} = 0.$

On solving the above algebraic equations with the aid of Maple or Mathematical, we have the following results:

Result 1:

$\begin{matrix} a_{0} = 0, a_{1} = \frac{2 k^{2} p}{γ}, r = \frac{ω^{2}}{4 k^{4}}, p = p, q = - 1, δ = \frac{γ^{2} k^{2}}{2 ω^{2}}, \\ μ = - \frac{1}{2} k^{2} p^{2}, A = - \frac{ω B}{2 k^{2}}, B = B, k = k, ω = ω . \end{matrix}$ (3.3)

Form this result, we have $p^{2} - 4 q r = p^{2} + \frac{ω^{2}}{k^{4}} > 0.$

Consequently, we have the following exact solutions:

$u_{1} (ξ) = - \frac{p ω}{γ} [\frac{(ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \tanh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{(- ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \tanh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}],$

$u_{2} (ξ) = - \frac{p ω}{γ} [\frac{(ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \coth (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{(- ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \coth (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}],$

$u_{3} (ξ) = - \frac{p ω}{γ} [\frac{(ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} (\coth (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) \pm c s c h (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ))}{(- ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} (\coth (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) \pm c s c h (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ))}],$

$u_{4} (ξ) = - \frac{p ω}{γ} [\frac{2 (ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} (\tanh (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + \coth (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ))}{2 (- ω + k^{2} p) + k^{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} (\tanh (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + \coth (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ))}],$

$u_{5} (ξ) = - \frac{p ω}{γ} [\frac{(ω + k^{2} p) - k^{2} (\frac{\pm \sqrt{\frac{(R^{2} + M^{2}) (p^{2} k^{4} + ω^{2})}{k^{4}}} - R \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \cosh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{R \sinh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + M})}{(- ω + k^{2} p) - k^{2} (\frac{\pm \sqrt{\frac{(R^{2} + M^{2}) (p^{2} k^{4} + ω^{2})}{k^{4}}} - R \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \cosh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{R \sinh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + M})}],$

$u_{6} (ξ) = - \frac{p ω}{γ} [\frac{(ω + k^{2} p) + k^{2} (\frac{\pm \sqrt{\frac{(R^{2} + M^{2}) (p^{2} k^{4} + ω^{2})}{k^{4}}} + R \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \sinh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{R \cosh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + M})}{(- ω + k^{2} p) + k^{2} (\frac{\pm \sqrt{\frac{(R^{2} + M^{2}) (p^{2} k^{4} + ω^{2})}{k^{4}}} + R \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} \sinh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{R \cosh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + M})}],$ $u_{7} (ξ) = - \frac{p ω}{γ} [\frac{\sqrt{p^{2} k^{4} + ω^{2}} \sinh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + (ω - p k^{2}) \cosh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{- \sqrt{p^{2} k^{4} + ω^{2}} \sinh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + (ω + p k^{2}) \cosh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}],$

$u_{8} (ξ) = - \frac{p ω}{γ} [\frac{(ω - p k^{2}) \sinh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + \sqrt{p^{2} k^{4} + ω^{2}} \cosh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}{(ω + p k^{2}) \sinh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) - \sqrt{p^{2} k^{4} + ω^{2}} \cosh (\frac{1}{2} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ)}],$

$u_{9} (ξ) = - \frac{p ω}{γ} [\frac{(ω - p k^{2}) \sinh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + \sqrt{p^{2} k^{4} + ω^{2}} (\cosh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) \pm 1)}{(ω + p k^{2}) \sinh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) - \sqrt{p^{2} k^{4} + ω^{2}} (\cosh (\sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) \pm 1)}],$

$u_{10} (ξ) = - \frac{p ω}{γ} [\frac{2 (ω - p k^{2}) \sinh (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) \cosh (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) + \sqrt{p^{2} k^{4} + ω^{2}} (2 \cosh^{2} (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) - 1)}{2 (ω + p k^{2}) \sinh (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) \cosh (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) - \sqrt{p^{2} k^{4} + ω^{2}} (2 \cosh^{2} (\frac{1}{4} \sqrt{p^{2} + \frac{ω^{2}}{k^{4}}} ξ) - 1)}],$

where $ξ = k x + ω t .$

Result 2:

$\begin{matrix} a_{0} = 0, a_{1} = \frac{(- ω + 3 k^{2} p) (A q - B p)}{γ A}, r = 0, p = p, q = q, δ = \frac{2 γ^{2} k^{2}}{{(- ω + 3 k^{2} p)}^{2}}, \\ A = A, B = B, μ = p (- ω + k^{2} p), k = k, ω = ω . \end{matrix}$ (3.4)

Since $r = 0$ and $p q \neq 0$ , then we have the following exact solutions:

$u_{11} (ξ) = \frac{(- ω + 3 k^{2} p) (A q - B p)}{γ} [\frac{- p d}{(A q - B p) d + A q (\cosh (p ξ) - \sinh (p ξ))}],$

$u_{12} (ξ) = \frac{(- ω + 3 k^{2} p) (A q - B p)}{γ} [\frac{- p (\cosh (p ξ) + \sinh (p ξ))}{A q d + (A q - B p) (\cosh (p ξ) + \sinh (p ξ))}],$

,p>where

$ξ = k x + ω t .$

Result 3:

$\begin{matrix} a_{0} = 0, a_{1} = \pm \frac{k (A q - B p) \sqrt{\frac{2}{δ}}}{A}, r = 0, p = p, q = q, A = A, B = B, \\ μ = k p (\sqrt{\frac{2 γ^{2}}{δ}} - 2 k p), k = k, ω = - k (\sqrt{\frac{2 γ^{2}}{δ}} - 3 k p), δ > 0. \end{matrix}$ (3.5)

,p>Since

$r = 0$ and

$p q \neq 0$ , then we have the following exact solutions:

$u_{13} (ξ) = \pm k (A q - B p) \sqrt{\frac{2}{δ}} [\frac{- p d}{(A q - B p) d + A q (\cosh (p ξ) - \sinh (p ξ))}],$

$u_{14} (ξ) = \pm k (A q - B p) \sqrt{\frac{2}{δ}} [\frac{- p (\cosh (p ξ) + \sinh (p ξ))}{A q d + (A q - B p) (\cosh (p ξ) + \sinh (p ξ))}],$

where $ξ = k x - k (\sqrt{\frac{2 γ^{2}}{δ}} - 3 k p) t .$

Result 4:

$\begin{matrix} a_{0} = - \frac{A γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})}, a_{1} = \frac{B γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})}, r = r, \\ p = p, q = q, A = A, B = B, μ = \frac{q γ^{2} (- A B p + q A^{2} + r B^{2})}{δ {(- p B + 2 A q)}^{2}}, \\ k = \frac{2 B \sqrt{\frac{γ^{2}}{8 δ}}}{- p B + 2 A q}, ω = \frac{B γ^{2}}{2 δ (- p B + 2 A q)}, δ > 0. \end{matrix}$ (3.6)

In this case, we deduce that Equation (1.1) has many types of the exact traveling wave solutions as follows:

Type 1: When $p^{2} - 4 q r > 0$ and $p q \neq 0$ or $q r \neq 0$ , we have

$u_{15} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A + A \sqrt{p^{2} - 4 r q} \tanh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ))}{2 A q - p B - B \sqrt{p^{2} - 4 r q} \tanh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ)}],$

$u_{16} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A + A \sqrt{p^{2} - 4 r q} \coth (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ))}{2 A q - p B - B \sqrt{p^{2} - 4 r q} \coth (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ)}],$

$u_{17} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A + A \sqrt{p^{2} - 4 r q} (\coth (\sqrt{p^{2} - 4 r q} ξ) \pm c s c h (\sqrt{p^{2} - 4 r q} ξ)))}{2 A q - p B - B \sqrt{p^{2} - 4 r q} (\coth (\sqrt{p^{2} - 4 r q} ξ) \pm c s c h (\sqrt{p^{2} - 4 r q} ξ))}],$

$u_{18} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (4 r q B + 2 p A + A \sqrt{p^{2} - 4 r q} (\coth (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) + \tanh (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ)))}{4 A q - 2 p B - B \sqrt{p^{2} - 4 r q} (\coth (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) + \tanh (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ))}],$

$u_{19} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A - \frac{A \sqrt{p^{2} - 4 r q} (- R \cosh (\sqrt{p^{2} - 4 r q} ξ) \pm \sqrt{R^{2} + M^{2}})}{R \sinh (\sqrt{p^{2} - 4 r q} ξ) + M})}{2 A q - p B + \frac{B \sqrt{p^{2} - 4 r q} (- R \cosh (\sqrt{p^{2} - 4 r q} ξ) \pm \sqrt{R^{2} + M^{2}})}{R \sinh (\sqrt{p^{2} - 4 r q} ξ) + M}}],$

$u_{20} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A + \frac{A \sqrt{p^{2} - 4 r q} (R \sinh (\sqrt{p^{2} - 4 r q} ξ) \pm \sqrt{R^{2} + M^{2}})}{R \cosh (\sqrt{p^{2} - 4 r q} ξ) + M})}{2 A q - p B - \frac{B \sqrt{p^{2} - 4 r q} (R \sinh (\sqrt{p^{2} - 4 r q} ξ) \pm \sqrt{R^{2} + M^{2}})}{R \cosh (\sqrt{p^{2} - 4 r q} ξ) + M}}],$

$u_{21} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (p B + 2 A) \cosh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ) - B r \sqrt{p^{2} - 4 r q} \sinh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ))}{(p A - 2 r B) \cosh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ) - A \sqrt{p^{2} - 4 r q} \sinh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ)}],$

$u_{22} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (p B + 2 A) \sinh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ) - B r \sqrt{p^{2} - 4 r q} \cosh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ))}{(p A - 2 r B) \sinh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ) - A \sqrt{p^{2} - 4 r q} \cosh (\frac{1}{2} \sqrt{p^{2} - 4 r q} ξ)}],$

$u_{23} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (p B + 2 A) \sinh (\sqrt{p^{2} - 4 r q} ξ) - B r \sqrt{p^{2} - 4 r q} (\cosh (\sqrt{p^{2} - 4 r q} ξ) \pm 1))}{(p A - 2 r B) \sinh (\sqrt{p^{2} - 4 r q} ξ) - A \sqrt{p^{2} - 4 r q} (\cosh (\sqrt{p^{2} - 4 r q} ξ) \pm 1)}],$

$u_{24} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} \times [A + \frac{B (2 r (p B + 2 A) \sinh (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) \cosh (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) - B r \sqrt{p^{2} - 4 r q} (2 \cosh^{2} (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) - 1))}{2 (p A - 2 r B) \sinh (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) \cosh (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) - A \sqrt{p^{2} - 4 r q} (2 \cosh^{2} (\frac{1}{4} \sqrt{p^{2} - 4 r q} ξ) - 1)}] .$

Type 2: When $p^{2} - 4 q r < 0$ and $p q \neq 0$ or $q r \neq 0$ , we have

$u_{25} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A - A \sqrt{4 r q - p^{2}} \tan (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ))}{2 A q - p B + B \sqrt{4 r q - p^{2}} \tan (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ)}],$ $u_{26} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A + A \sqrt{4 r q - p^{2}} \cot (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ))}{2 A q - p B - B \sqrt{4 r q - p^{2}} \cot (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ)}],$ $u_{27} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A - A \sqrt{4 r q - p^{2}} (\tan (\sqrt{4 r q - p^{2}} ξ) \pm \sec (\sqrt{4 r q - p^{2}} ξ)))}{2 A q - p B + B \sqrt{4 r q - p^{2}} (\tan (\sqrt{4 r q - p^{2}} ξ) \pm \sec (\sqrt{4 r q - p^{2}} ξ))}],$ $u_{28} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 r q B + p A + A \sqrt{4 r q - p^{2}} (\cot (\sqrt{4 r q - p^{2}} ξ) \pm \csc (\sqrt{4 r q - p^{2}} ξ)))}{2 A q - p B - B \sqrt{4 r q - p^{2}} (\cot (\sqrt{4 r q - p^{2}} ξ) \pm \csc (\sqrt{4 r q - p^{2}} ξ))}],$ $u_{29} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (2 (2 r q B + p A) + A \sqrt{4 r q - p^{2}} (\cot (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) - \tan (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ)))}{2 (2 A q - p B) - B \sqrt{4 r q - p^{2}} (\cot (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) - \tan (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ))}],$ $u_{30} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} \times [A + \frac{B ((2 r q B + p A) (M + R \sin (\sqrt{4 r q - p^{2}} ξ)) - A \sqrt{4 r q - p^{2}} (- R \cos (\sqrt{4 r q - p^{2}} ξ) \pm \sqrt{R^{2} - M^{2}}))}{(2 A q - p B) (M + R \sin (\sqrt{4 r q - p^{2}} ξ)) + B \sqrt{4 r q - p^{2}} (- R \cos (\sqrt{4 r q - p^{2}} ξ) \pm \sqrt{R^{2} - M^{2}})}],$

$u_{31} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} \times [A + \frac{B ((2 r q B + p A) (M + R \sin (\sqrt{4 r q - p^{2}} ξ)) + A \sqrt{4 r q - p^{2}} (R \cos (\sqrt{4 r q - p^{2}} ξ) \pm \sqrt{R^{2} - M^{2}}))}{(2 A q - p B) (M + R \sin (\sqrt{4 r q - p^{2}} ξ)) - B \sqrt{4 r q - p^{2}} (R \cos (\sqrt{4 r q - p^{2}} ξ) \pm \sqrt{R^{2} - M^{2}})}],$

$u_{32} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (2 A + p B) \cos (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ) + B r \sqrt{4 r q - p^{2}} \sin (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ))}{(A p - 2 r B) \cos (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ) + A \sqrt{4 r q - p^{2}} \sin (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ)}],$ $u_{33} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (2 A + p B) \sin (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ) - B r \sqrt{4 r q - p^{2}} \cos (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ))}{(A p - 2 r B) \sin (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ) - A \sqrt{4 r q - p^{2}} \cos (\frac{1}{2} \sqrt{4 r q - p^{2}} ξ)}],$ $u_{34} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (2 A + p B) \cos (\sqrt{4 r q - p^{2}} ξ) + B r \sqrt{4 r q - p^{2}} (\sin (\sqrt{4 r q - p^{2}} ξ) \pm 1))}{(A p - 2 r B) \cos (\sqrt{4 r q - p^{2}} ξ) + A \sqrt{4 r q - p^{2}} (\sin (\sqrt{4 r q - p^{2}} ξ) \pm 1)}],$ $u_{35} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} [A + \frac{B (r (2 A + p B) \sin (\sqrt{4 r q - p^{2}} ξ) - B r \sqrt{4 r q - p^{2}} (\cos (\sqrt{4 r q - p^{2}} ξ) \pm 1))}{(A p - 2 r B) \sin (\sqrt{4 r q - p^{2}} ξ) - A \sqrt{4 r q - p^{2}} (\cos (\sqrt{4 r q - p^{2}} ξ) \pm 1)}],$ $u_{36} (ξ) = - \frac{γ (- A B p + q A^{2} + r B^{2})}{δ (- p B + 2 A q) (A^{2} + r B^{2})} \times [A + \frac{B (2 r (2 A + p B) \sin (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) \cos (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) - B r \sqrt{4 r q - p^{2}} (2 \cos^{2} (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) - 1))}{2 (A p - 2 r B) \sin (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) - A \sqrt{4 r q - p^{2}} (2 \cos^{2} (\frac{1}{4} \sqrt{4 r q - p^{2}} ξ) - 1)}] .$

Type 3: When $r = 0$ and $p q \neq 0$ , we have

$u_{37} (ξ) = - \frac{γ (- B p + q A)}{δ (- p B + 2 A q)} [1 + \frac{B p d}{(A q - B p) d + A q (\cosh (p ξ) - \sinh (p ξ))}],$

$u_{38} (ξ) = - \frac{γ (- B p + q A)}{δ (- p B + 2 A q)} [1 + \frac{B p (\cosh (p ξ) + \sinh (p ξ))}{A q d + (A q - B p) (\cosh (p ξ) + \sinh (p ξ))}],$

where $ξ = (\frac{2 B}{- p B + 2 A q} \sqrt{\frac{γ^{2}}{8 δ}}) x + (\frac{B γ^{2}}{2 δ (- p B + 2 A q)}) t$ .

Type 4: When $r = p = 0$ and $q \neq 0$ , we have

$u_{39} (ξ) = - \frac{γ}{2 δ} [1 + \frac{B}{A q ξ + A c_{1} - B}],$

where $ξ = \frac{B}{A q} \sqrt{\frac{γ^{2}}{8 δ}} x + \frac{B γ^{2}}{4 δ A q} t$ .

Physical explanations of our obtained solutions

The obtained exact traveling wave solutions for the nonlinear KPP equation (1.1) are hyperbolic, trigonometric and rational. In this section, we have presented some graphs of the exact solutions $u_{1} (x, t)$ , $u_{7} (x, t)$ , $u_{11} (x, t)$ , $u_{14} (x, t)$ , $u_{16} (x, t)$ , $u_{19} (x, t)$ , $u_{25} (x, t)$ and $u_{31} (x, t)$ constructed by taking suitable values of involved unknown parameters to visualize the mechanism of the original equation (1.1). These solutions are kink, singular kink-shaped soliton solution, hyperbolic solutions and trigonometric solutions. For more convenience the graphical representations of these solutions are shown in the following figures 1 to 8:

Figure 1 Plot of the solution $u_{1} (x, t)$ when $k = 2, p = ω = 1, γ = - 1.$

Figure 2 Plot of the solution $u_{7} (x, t)$ when $k = 1, p = 3, ω = 2, γ = - 1.$

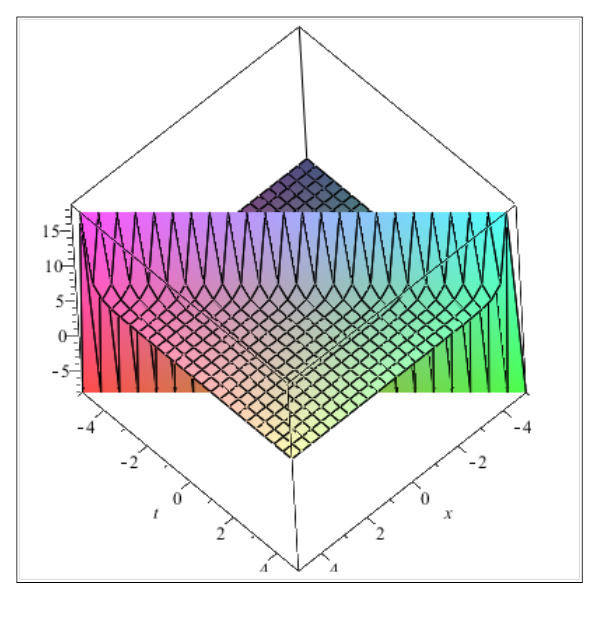
Figure 3 Plot of the solution $u_{11} (x, t)$ when $k = 1, p = 3, q = 4, ω = 1,$ $γ = - 3, d = 1,$ $B = 2, A = 1.$

Figure 4 Plot of the solution $u_{14} (x, t)$ when $k = 1, p = 1, δ = 2, q = 3,$ $γ = - 1, d = 3, B = 1, A = 2.$

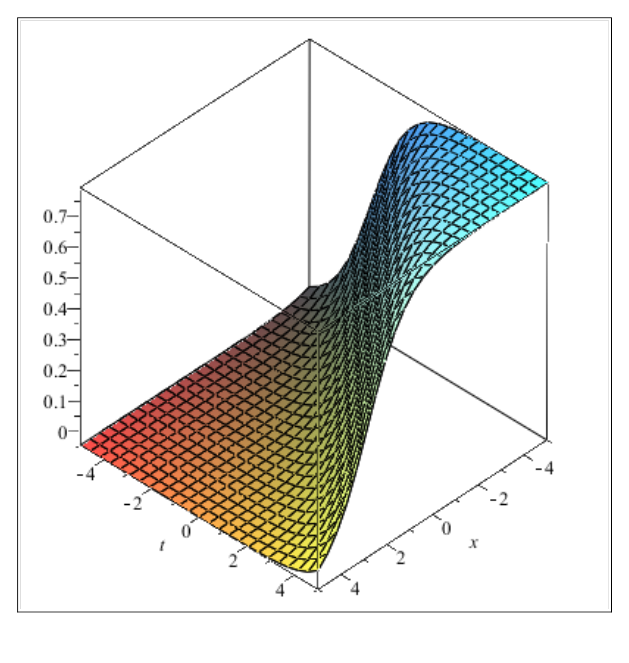
Figure 5 Plot of the solution $u_{16} (x, t)$ when $p = 3, δ = 4, q = 1,$ $γ = - 3, r = 1, B = - 2, A = - 1.$

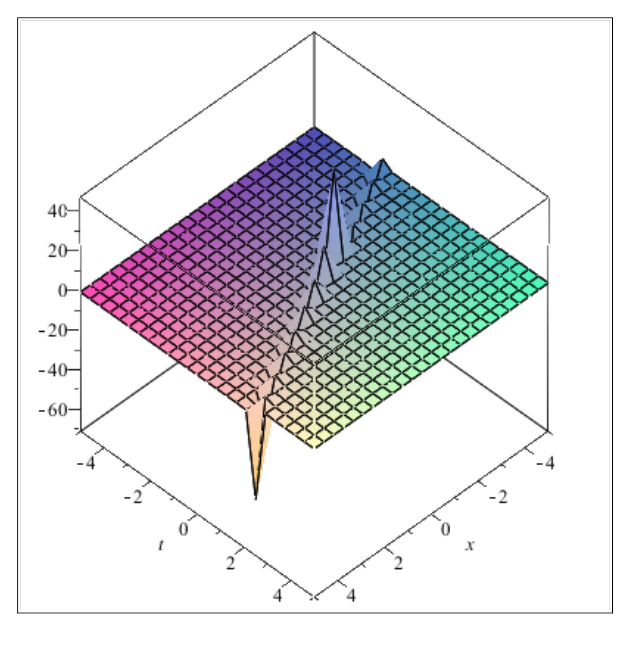
Figure 6 Plot of the solution $u_{19} (x, t)$ when $p = 5, δ = 1, q = 1, γ = - 3, r = 1, B = 2, A = 2, R = 2, M = 2.$

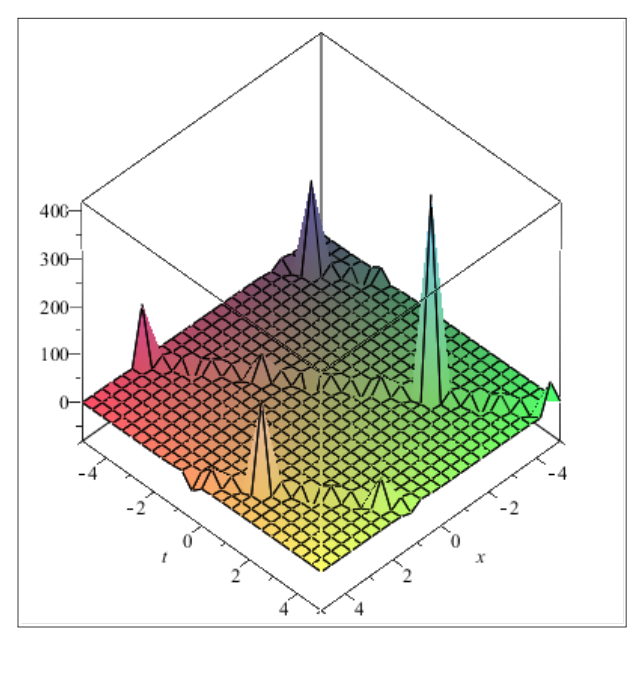
Figure 7 Plot of the solution $u_{25} (x, t)$ when $p = 1, δ = 1, q = 5,$ $γ = 1, r = 4, B = 3, A = 2.$

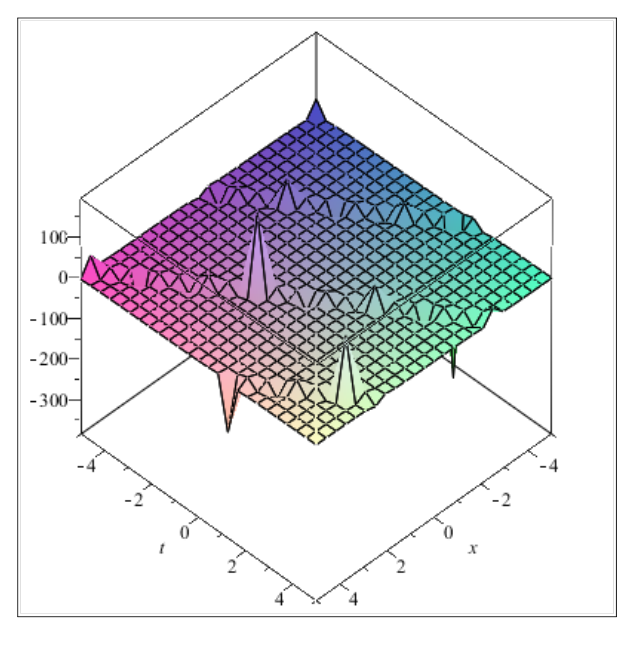
Figure 8 Plot of the solution $u_{31} (x, t)$ when $p = 1, δ = 1, q = 2,$ $γ = 1, r = 4,$ $B = 2, A = 2, R = 3, M = 2.$

Conclusion

In this article, we have employed the Bäcklund transformation of the generalized Riccati equation to obtain many new exact traveling wave solutions of the nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation (1.1). On comparing our results in this paper with the well-known results obtained in²²^,²⁶^,⁴⁶ we deduce that our results in this article are new and are not published elsewhere. The Bäcklund transformation of the generalized Riccati equation obtained in this article is more effective and gives more exact solutions than the generalized Riccati equation mapping method obtained in.⁴¹^–⁴⁵ Further, all solutions obtained in this article have been checked with the Maple by putting them back into the original equations. Finally, the proposed method in this article can be applied to many other nonlinear PDEs in mathematical physics, which will be done in forthcoming papers.