Einstein’s clock synchronization procedure has led to the contention of conventionalism that clock synchronization is arbitrary and, thus, the one-way speed of light cannot be measured even in principle. In the context of relativistic theories, we analyze the linear Sagnac effect and show that its interpretation implies the existence of superluminal light speeds. Furthermore, we consider an experiment of the Sagnac type that can test the second postulate of special relativity by discriminating absolute synchronization from Einstein synchronization. The mere existence in principle of such a test settles the nearly century-long controversy about the conventionality of the one-way speed of light. An immediate consequence is that the one-way speed is measurable and the Lorentz transformations maintain their unique physical meaning and, thus, cannot be substituted by transformations based on absolute synchronization. The outcome of the experiment, attainable with present technology, will either corroborate the postulate of a universal light speed in all inertial frames or identify the preferred frame of reference of relativistic theories. PACS: 03.30.+p; 03.65.-w; 45.50.-j

Keywords: sagnac effect, relativistic theories, one-way speed of light, Einstein synchronization

A theory is physically meaningless unless its basic postulates can be tested, i.e., verified experimentally. This procedure is sometimes referred to by saying that the theory can be falsified. The second postulate of the special theory of relativity reflects Einstein’s assumption that the universal one-way speed of light c is constant. With the exception of experts, many physicists believe that the speed of light measured in experiments refers to the one-way speed,¹ while what is measured is the round-trip value,² in accordance with Einstein synchronization procedure using a mirror on a round-trip flight path. In fact, Einstein did not provide a way to test his basic assumption. Instead, by proposing his well-known clock synchronization procedure, spatially separated clocks are conventionally synchronized by assuming that the average round-trip speed and the one-way speed are the same. Considering that, in principle, the two speeds (round-trip and one-way) may not be the same, the question of whether or not the one-way speed of light is measurable, represents one of the prominent controversial debates of modern physics. The conventionality of the synchronization procedure of spatially separated clocks in special relativity (SR), and the related measurement of the one-way speed of light, has been thoroughly discussed by Poincaré³ and Einstein,⁴ and reinforced in the works of Reichenbach,⁵ and Grünbaum.⁶ Discussions on this fundamental issue were revived by the works of Möller⁷ and Mansouri and Sexl,⁸ who confirmed that synchronization by means of clock transport, is equivalent to Einstein’s procedure, favoring the conventionalist view.

According to Mansouri and Sexl,⁸ the intrinsic indetermination in the one-way speed c renders the validity of the second postulate of SR not testable. This has led to a renaissance of alternative relativistic theories that assume the existence of a preferred frame where space and light speed are isotropic while, in a relatively moving inertial frame, they are no longer isotropic. Thus, physicists have focused their attention to preferred frame theories that use transformations with the same rod-contraction and clock-retardation as the Lorentz transformation (LT), but differ from it by an arbitrary synchronization parameter. By their very construction, preferred frame theories interpret all the known experiments that support SR. For example, in the Michelson-Morley experiment, the observable turns out to be independent from synchronization. Therefore, besides the Lorentz transformations, also the transformations based on absolute synchronization, such as the Tangherlini transformations (TT),⁹ provide the same null result of SR. What matters in this and in other optical experiments is the average speed on the optical path, which turns out to be exactly c with transformations (such as the TT) that foresee the Lorentz-Fitzgerald contraction of moving rods and the time dilation of moving clocks. One important contribution to the subject was given by Bell,¹⁰ who stated that although there is a stringent “difference in philosophy” between the view of SR and that of a preferred frame theory, “The facts of physics do not oblige us to accept one philosophy rather than the other”. Bell’s assertion was used as a starting point in a series of works adopting the conventionalist thesis within relativistic theories,^10–14 where it has been argued that there is essentially one theory, Bell’s two philosophies corresponding rather to different aspects of the same theory.^11–19

If synchronization is arbitrary and the two synchronizations (Einstein’s and absolute) are equivalent, important consequences arise. Indeed, the Lorentz covariance concept exploits the symmetry of the Lorentz group and is usually applied by theoreticians to several branches of modern physics. If Einstein and absolute synchronizations are physically indistinguishable, the LT could be equivalently substituted by the TT, which possesses a lower symmetry, similar to that of the Galileo group. In this case, the equivalence of the two synchronizations implies that what is important is the contraction of moving rods and the slowing down of moving clocks but not the symmetry of the transformations. This fact is hardly acceptable for most physicists who have been relying for decades on the properties of the Lorentz group. There are instances in the literature where, instead of the LT, the TT transformations are equivalently used to describe physical reality. In the context of relativistic theories, an example is found in the interpretation of the Sagnac²⁰ effect by Kassner,²¹ who proposes to solve Selleri’s^22,23 paradox by replacing Einstein synchronization with the absolute synchronization. Kassner’s conclusion is then that the light speeds c+v and c−v, pointed out by Selleri in his paradox, are to be interpreted in terms of the arbitrariness of synchronization and, thus, do not invalidate the second postulate of SR that requires the unique, universal value c for the speed of light.

Kassner’s paper is important for two reasons. First, he makes it evident that the approach of conventionalism has spread in the literature even among journals of didactic nature. Second and most importantly, because it supports the opinion shared by many physicists that within relativistic theories the principle of relativity remains valid even when we adopt a synchronization procedure different from that of Einstein, regardless of the validity or not of Einstein’s second postulate. In this complex scenario, the important issue consists in clarifying the physical equivalence — or lack thereof — of preferred frame theories with standard SR (i.e., special relativity with Einstein synchronization). The purpose of our paper is to show that, at least in principle and even on a kinematical basis,^24–27 there are experiments capable of testing the one-way speed of light, and the Sagnac effect is one of them. In Sects. 2 and 3 we consider the relativistic interpretation of the Sagnac effect, using a "linearized" version of it, and discuss the related controversial problem of the superluminal speeds of the light signals, highlighted by detractors of Einstein synchronization as disproving the validity of Einstein’s second postulate.

In Sect. 4 we show that an experiment of the Sagnac type can discriminate Einstein synchronization from absolute synchronization, i.e., standard SR from identifiable preferred frame theories. If the experiment is performed, its outcome will have significant consequences on modern physics. The first important result is that, from a theoretical perspective and in the description of physical theories, the LT are not equivalent to and cannot be arbitrarily replaced by the TT. In fact, if the one-way speed of light is observable, even only in principle, the validity of the second postulate of special relativity can be tested. Thus, standard SR maintains its unique meaning, physically different from that of theories that assume the existence of an identifiable preferred frame. Finally, we provide an indication of the sensitivity required by the experimental setup, capable of detecting in certain situations the velocity of the preferred frame if it were to exist.

The usual circular Sagnac experiment is pictured in Figure 1. Consider a disk rotating at constant angular velocity ω and an observer with a clock O∗ stationary on a point at radius R, the origin of a co-rotating reference frame S∗. As indicated in Figure 1, this observer sends two light signals (as in the Sagnac experiment), or two particles (or two clocks, as in the Hafele-Keating experimen²⁸) at velocity C around the disk circumference in opposite directions, respectively. Equivalently, we may consider the Sagnac experiment performed in a conveyor belt, as shown in Figure 2, which has been used to describe a modified, but equivalent, "linearized" version of the Sagnac effect.²⁹

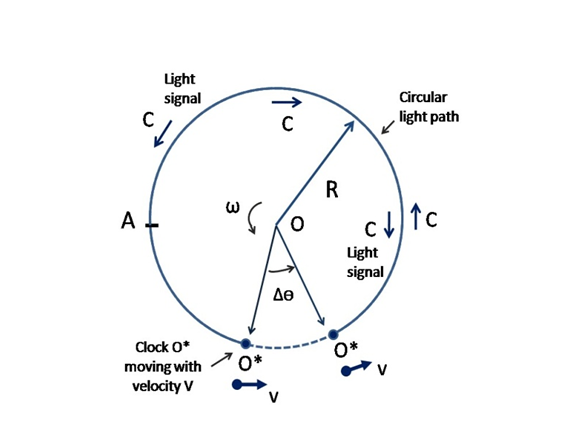
Figure 1 Clock O∗(originally at point A) is fixed on the circumference of the disk of radius Rrotating counter-clockwise at the angular velocity ωwith respect to the laboratory frame S. Two light signals are sent around the circumference of the disk in opposite directions starting from clock O∗, which measures the time span on the return of each signal to O∗.

We wish to know the time span observed by O∗ on the return of each signal on the disk. First, we consider the description given by an inertial observer O at the center of the disk stationary in the laboratory frame S. The observer O∗ at R is co-moving with the disk with angular velocity ω and possesses the tangential speed $v=\omega R$ . If the laboratory frame S is chosen as the preferred frame, the description of the Sagnac effect and corresponding time span variation$\Delta t=t_{-}-t_{+}$ in such a frame is the same for Newtonian mechanics and relativistic theories with any synchronization. In general, with different speeds $C_{+}$ and $C_{-}$ in the counter-rotating (+ clockwise) and co-rotating (- counterclockwise) directions, respectively, the result, for the propagation time $t_{+}$ and $t_{-}$ of the signal in S, is

$c_{\pm }=\frac{2\pi \gamma R}{t_{\pm }^{*}}\simeq c\pm v,$ (1)

where $L=\pi R$ and $\Delta t=t_{-}-t_{+}$ The local time of O∗ runs slower than the time of O by the time dilation factor , so that for O∗ the light signals take the times$t_{\pm }^{*}=t_{\pm }/\gamma$  and,

$\Delta t^{*}=t_{-}^{*}-t_{+}^{*}=\frac{2L\left(C_{+}-C_{-}+2v\right)}{\gamma (C_{+}+v)\left(C_{-}-v\right)}\Rightarrow \frac{4\gamma Lv}{c^2},$ (2)

where$\Delta t^{*}$ is the time span variation measured by the clock O∗ and the last term corresponds to the case$C_{+}=C_{-}=c$ .

With reference to Figure 1, for the observer O∗ on the disk at$r=R$ , the circumference length corresponds to the proper ground length of the path followed by the signals and is given by$2\pi \gamma R$ . For the usual case $C_{+}=C_{-}=c$  , the time spans are$t_{\pm }=2\pi R/\left(c\pm v\right)$ . Then, for the Sagnac effect, the average speeds of light in the counter- and co-rotating senses are

$c_{\pm }=\frac{2\pi \gamma R}{t_{\pm }^{*}}$ ≃ $c\pm v$ ,(3)

Where the results $c\pm v$ correspond to the speed of light in vacuum, $C=c.$

Different interpretations of the sagnac effect

Besides other properties, the Sagnac effect is widely recognized as an optical experiment capable of indicating the state of rotation of the interferometer.³⁰ We mention here only some of the several contrasting interpretations of the Sagnac effect, originally thought to disprove special relativity.²⁰ Landau and Lifshitz³¹ trace the physical cause of the existence of the Sagnac effect in the rotating reference system as due to a difference between the velocities of counter-propagating waves. This velocity difference, which refers to the average velocities in (3), leads to a paradox according to the interpretation of Selleri,²² who shows that when the radius of the rotating disk is increased to R → ∞ keeping constant $\omega R=v$ , the local speed of light in an inertial frame would be c + vor c − vdepending on the direction of propagation, in disagreement with the unique value c foreseen by the second postulate of special relativity. The existence of Selleri’s paradox has been supported by other papers^32-37 where the authors claim that the phase difference of counter-propagating waves in the reference system co-rotating with a ring interferometer, calculated in the context of standard SR, is equal to zero. Instead, Malykin³⁸ argues that we are rather in the presence of a Zeno paradox because, considering that the rotating disk is not an inertial frame, the interpretation of the Sagnac effect is reliant on the equivalence principle and the effect of time dilation in a gravitational field.

The argument against Einstein synchronization can be resumed as follows. Because of the motion of O∗, for the observer O of the laboratory frame S, the paths ± of the signal have different lengths, $2\pi R/\left(1\pm v/c\right)$ and, since the velocity c of the signal is the same in both directions, it appears obvious that we must have different propagation times t±. For O∗, instead, the propagation paths have the same length $2\pi \gamma R$ but still we have different propagation times, $t_{\pm }^{*}=t_{\pm }/\gamma$ . Thus, for propagation on paths of the same lengths, if the respective propagation times, $t_{\pm }^{*}$ , are different, different speeds $c_{\pm }$ (and not the same speed c) are expected. This argument, which seems to cast doubts about the validity of a universal constant speed of light c, has been expanded by Selleri who claims that the paradox can be solved only if relativistic theories adopt the "natural" absolute synchronization that foresees the different speeds$$$$c + v and c - v of expression (3).

In this context, it is worth recalling the arguments of Kassner about Selleri’s paradox. In rebutting Selleri’s claim, Kassner²¹ attempts to refute the paradox by explaining the Sagnac effect in the frame of the co-moving observer O∗ in two ways: through Minkowsky’s analysis and by means of the absolute synchronization. The point is that, if Einstein synchronization is applied along the closed circular path, the resulting average speed in (3) is c, and not c + v or c - v. Thus, in this case, the Sagnac effect invalidates standard SR. After his Minkowsky analysis, Kassner concludes by acknowledging that “Einstein synchronization fails when performed along a path around a full circle”, i.e., on a closed path on the rotating disk, a failure that has also been observed by Weber³⁹ and earlier by Anandan.⁴⁰

Thus, in order to account for the resulting unphysical time discontinuity arising from the speeds $c+v$ and $c-v$ and solve Selleri’s paradox, Kassner introduces the unusual concept of a “time gap” on the rotating disk and states, “the speed of light is c everywhere except at the point on the circle where we put the time gap. The position of this point is arbitrary but there must inevitably be such a point.”

The solution based on Minkowsky’s analysis presented by Kassner has been objected to by Gift⁴¹ who rejects Kassner’s adjustable “time gap” based on an unphysical time discontinuity claiming that is a theoretical construct that has no basis in reality. Similarly, Selleri has claimed that "it is not true that the synchronization procedure can be chosen freely because Einstein convention leads to an unacceptable discontinuity in the physical theory". Moreover, according to Selleri "Very probably the above discontinuity is the origin of the synchronization problems met with by the Global Positioning System". In relation to this, Gift emphasizes that the failure of Einstein synchronization is well known to GPS engineers who discovered^41,42 that they cannot synchronize GPS clocks fixed on the rotating Earth using Einstein synchronization.^43,44

The second argument presented by Kassner²¹ to solve Selleri’s paradox consists of replacing Einstein synchronization with the absolute synchronization. Thus, instead of the Lorentz transformations and without citing the related literature, Kassner makes use of the Tangherlini transformations. Considering that the one-way speed of light is synchronization dependent, for Kassner a difference from c does not constitute a problem because the observable two-way (average) speed of light remains c, as in the interpretation of the Michelson-Morley experiment. In fact, if synchronization is arbitrary (as also assumed by Kassner), the two synchronizations are equivalent and provide the same observable result, as they actually do within Kassner’s basic set up and hypotheses. Then, although acknowledging the anisotropy due to the different speeds c+v and c−v in Selleri’s paradox, Kassner argues that the difference is to be interpreted in terms of the arbitrariness of synchronization and, thus, does not invalidate the second postulate of special relativity. Yet, in Sect. 4 we demonstrate that, in general, Einstein synchronization and the absolute synchronization are not physically equivalent. Therefore, the assumption of conventionalism is groundless, so that Kassner’s argument based on it is untenable. Moreover, while adhering to the conventionality of the speed of light and the equivalence of the two synchronizations, Kassner does not discuss the consequences of this assumption on the countless physical theories traditionally based on the LT. These physical theories would be substantially modified if they were based on and developed by means of the TT. In the next section, we review the arguments in favor and against Einstein synchronization and the problem of superluminal speeds within the context of the "linearized" Sagnac effect, shown in Figure 2.

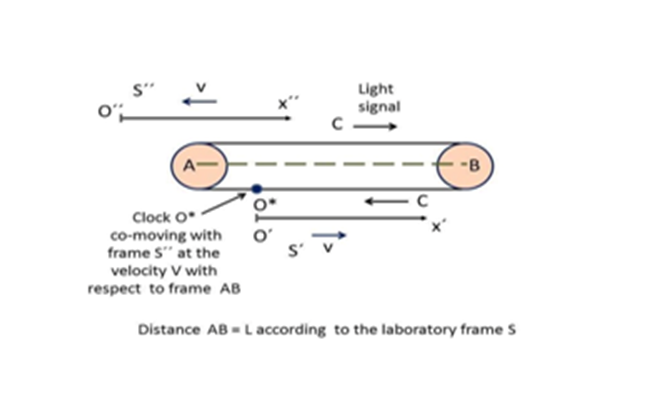
Figure 2 The conveyor belt system represents a "linearized" version of the Sagnac effect. The belt stands for a flexible tube and the signals propagate in opposite directions along the closed path inside the tube, acting as a wave-guide and rotating counter-clockwise while leaning over the two pulleys separated by the arm AB of fixed length L. The inertial frame S’’ is co-moving with the upper part of the tube with velocity vwith respect to the arm AB, stationary in the laboratory frame S, while frame S’ and clock O*are co-moving with the lower part of the tube in the opposite direction.

With reference to Figure 2, we assume that, if the distance L between the two pulleys of small radius r is long enough (r << L), the time $\tau \simeq R/v$ spent by the signals in the short portion of the tube in contact with the pulleys will be negligible with respect to the total time of flight and we may omit it. Furthermore, the acceleration $a=v^2/r$ that could cause a change in the flow of time of clocks co-moving with the tube is constant and depends on vand r. Therefore, the change due to the effect of the acceleration does not depend on L and, if the distance L is long enough, becomes negligible with respect to the time variation $\Delta t^{\ast }$ , proportional to L, observed in the Sagnac effect.

If the tube where the light signals propagate is filled with a co-moving medium (for example, a fluid of refractive index n where the local speed of light is $C^0=c/n$ ) the speed of light is no longer c but C0. In this more general case, the two signals circumnavigate the tube in opposite directions with the same local (ground) speed $C^{*}=C^0$ with respect to the tube.

1. For special relativity with the LT.

For simplicity we consider here the case $C^0=c$ We have,

$t_{+}=\frac{2L}{c+v};t_{-}=\frac{2L}{c-v}$ (4)

$\Delta t^{*}=\frac{\Delta t}{\gamma }=\frac{t_{-}-t_{+}}{\gamma }=4\gamma \frac{vL}{c^2}$  (5)

It can be shown that the Sagnac effect, related to $\Delta t^{*}$ is foreseen to be independent of the signals ground speed $C^0$ , for both the circular and linear cases.

2. For a preferred frame theory based on the TT.

The TT between the preferred frame Sand the moving frame S′ are:$x\text{'}=\gamma \left(x-vt\right);y\text{'}=y;z\text{'}=z;t\text{'}=t/\gamma$ . Using the TT, with $C_{+}=C^0/{\gamma }^2-v$ and $C_{-}=C^0/{\gamma }^2+v$ , we have

$t_{+}=\frac{2L}{C_{+}+v}=\frac{2{\gamma }^{2}L}{C^0};t_{-}=\frac{2L}{C_{-}-v}=\frac{2{\gamma }^{2}L}{C^0}$

$\Delta t^{*}=\frac{\Delta t}{\gamma }=\frac{t_{-}- t_{+}}{\gamma }=0,$

which implies no Sagnac effect independently of $C^0$ , the same result as in Newtonian mechanics.

From a mathematical perspective, the internal consistency of the LT is not questionable and not questioned here. In the following, we try to adopt an objective point of view, simply presenting the arguments in favor or against Einstein synchronization, with the aim of clarifying the issue of superluminal average speeds in the context of the Sagnac effect. The incompatibility of Einstein synchronization over a closed path has been discussed above in Sect. 2. The objection that could be made in the context of the circular Sagnac effect is that the rotating frame is a non-inertial frame and, thus, Einstein synchronization is not applicable in such a frame. Here, with the linear Sagnac effect, we may apply Einstein synchronization separately to the inertial frames S′′ and S′ co-moving respectively with the upper and lower part of the tube. Still, we find that the mentioned incompatibility subsists and we are met once more with superluminal speeds and the conflicting point of views, or "realities", of S’and S’’.

The Lorentz transformations from S’’ to S’ are,

$x^{\prime }={\gamma }^{\prime }\left(x^{″}-w{t}^{″}\right);t^{\prime }={\gamma }^{\prime }\left(t^{″} - \frac{w{x}^{″}}{c^2}\right),$ (6)

with$w=2v/\left(1+v^2/c^2\right)$  and$\gamma \text{'}={\left(1-w^2/c^2\right)}^{-1/2}={\gamma }^2\left(1+v^2/c^2\right)$ .

The crucial question for standard SR is: How does the observer O∗ manage to explain the observed time span difference for two signals counter-propagating along a path of the same length and with the same ground speed $C^0=c?$

For our example, we choose a special case where the effect of non-conservation of simultaneity is made apparent. For theexperimental set-up shown in Figure 3, we assume that the three origins O, O′, O′′ of frames S, S’, S’’, coincide at the initial time $t=t^{\prime }=t^{\prime \prime }=0$ , while the pulley at A is positioned at the distance $L_o=vL/C^0=vL/c$ to the left with respect to O, and the pulley at B at the distance $L-L_o=L\left(1-v/C^0\right)=L\left(1-v/c\right)$ to the right. For our purposes, it is sufficient to consider the clockwise propagation of a light signal and determine its time of flight starting from the clock $O^{\ast }$ , co-moving with the tube and coincident with the origin $O^{\prime \prime }$ at$t^{\prime \prime }=0$ , and returning to $O^{\ast }$ after a complete cycle. The single clock O∗ alone is used to determine the time interval of the closed trip and, therefore, no synchronization procedure is involved. The two physical realities of S’’ and S’ will be confronted.

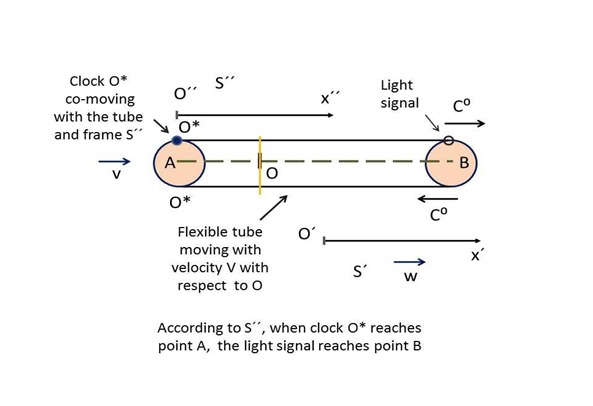
Figure 3 The linear Sagnac effect described from the perspective of frame S′′. The arm AB of length L, fixed in the laboratory frame S, moves with velocity vwith respect to S’’, stationary with the upper part of the tube. Frame S’, co-moving with the lower part of the tube, moves with velocity w with respect to S′′ and velocity v with respect to S. The origins O′′, O′ coincide with the origin O of frame S at t = t′ = t′′=0, when

the light signal is sent counter-propagating at the velocity $C^0=c$ . At the time$t_B^{\text{'}\text{'}}=t_A^{\text{'}\text{'}}$ , the signal has reached point B while clock O∗ has simultaneously reached point A.

Physical reality and total time for the clockwise trip according to S’’

Clocks at rest in some inertial reference frame may be “internally” synchronized according to Einstein’s procedure. Without reference to other inertial frames in relative motion, to say that the clocks at rest along the x′′ of the inertial frame S’’ are synchronized, it implies, for both Newton and Einstein, that in S’’ the clocks show the same readings simultaneously. Within a given inertial frame, “internal” simultaneity or, simply, simultaneity, is a reflection of internally synchronized clocks. Then, physical phenomena are described in S’’ as a function of the time t′′, the same time simultaneously displayed by all the synchronized clocks. If a hypothetical signal is sent at infinite speed along the x′′ axis of S’’, all the synchronized clocks on the x′′ axis will display the same time simultaneously when the signal passes by. At least in principle, clocks can be properly (internally) synchronized by signals with either finite or infinite speed, if the latter were available. The same conclusions apply for S’. For both Newton and Einstein, the concept of (internal) simultaneity applies when keeping within the physical reality of any inertial frame. The difference between Newton and Einstein shows up only when we relate two inertial frames in relative motion by means of the space-time coordinates transformations. In fact, as is well-known, if the hypothetical signal sent along the x′′ axis of S’’ had infinite speed also along the x′ axis of S’, there would be a conflict with the Lorentz transformations that assume the relativity of time and foresee different, non-simultaneous time readings between the two sets of clocks of S’’and S’. Supporters of special relativity overcome this problem by arguing that a signal with infinite speed is not operationally acceptable within the theory, which requires c to be the maximum speed permitted. However, given that the concept of simultaneity holds (internally) for both Newton and Einstein when keeping within the physical reality of a given frame, we may say that physical phenomena are portrayed in that frame as a function of the same "absolute" time. Thus, the restriction imposed by the finite speed c does not impede to conceive that, if spatially separated clocks are synchronized, they will display the same time simultaneously when a hypothetical infinite-speed signal passes by. The same is true for the synchronized clocks of any other inertial frame.

What is to expect in any case, is that the related physical realities of the two inertial frames in relative motion are compatible and reflect the same objective physical reality. In our analysis of the linear Sagnac effect, we shall consider the compatibility of the internal simultaneity of an inertial frame S’’ with that of another generic inertial frame S’ in relative motion with respect to S’’. As shown below, we find that internal simultaneity is not compatible with Einstein synchronization and the Lorentz transformations, because the latter imply, for S’’ and S’, two contrasting and irreconcilable physical realities.

We calculate now the time taken by the signal to reach point B after leaving the clock O∗. Since, at $t^{\prime \prime }=0$ point B is at the distance L(1−v/c)/γ to the right from the origin $O^{\prime \prime }=O^{\ast }$ and point A is at vL/γc to the left, the signal reaches B at the time

$t_B^{\text{'}\text{'}}=\frac{L}{\gamma c}=t_A^{\text{'}\text{'}}$ (7)

and at the same time $t_A^{\text{'}\text{'}}$  clock $O^{\ast }=O^{\prime \prime }$ reaches point A, the two events at A and B being simultaneous. In the time span $t_B^{\text{'}\text{'}}$  the signal has covered the ground length $L/\gamma$ of the upper part AB of the tube at the local speed c. As shown in Figure 3, after the clock O∗, initially co-moving with the origin O′′, reaches point A, it turns around the pulley and goes toward point B, co-moving now with the lower part AB of the tube and the x′ axis of S′.

Frame S’’and S′ agree on and share the common value for the total invariant proper length 2γL of the tube where propagation takes place. It follows that both S’’ and S′ agree that, after changing direction at B, the signal is bound to cover the remaining proper length $L\text{'}=2\gamma L-L/\gamma =\gamma \text{'}L/\gamma$  from B to O∗ by traveling entirely in the lower part of the tube until clock O∗ is met, as apparent from Figures 3, 4, and 5. For S’’, the ground length of the lower part of the tube is${\gamma }^{\prime }L/\gamma$ , which (because of its relative motion) is seen as being contracted by the factor ${\gamma }^{\prime }$ to $L/\gamma$ and, thus, it fits exactly the length $L/\gamma$ of the segment AB. Conversely and in contrast with the reality of S’’, frame S′ estimates that it is the upper part of the tube that has ground length ${\gamma }^{\prime }L/\gamma$ , seen by S′ as being contracted by the factor ${\gamma }^{\prime }$ to the value $L/\gamma$ . At this point, detractors of Einstein synchronization may point out the following two arguments against the validity of Einstein synchronization.

1. They may first argue that the time interval $\Delta t^{\prime }$ , corresponding to propagation in the lower part of the tube, can be inferred by S’’, knowing that the ground speed is c also in that lower section of the tube. In fact, the ground length of the lower part of the tube, $L^{\prime }={\gamma }^{\prime }L/\gamma$ , to be covered by the signal, and the corresponding ground speed c of the signal are known. Thus, an observer of S’’ may say that, whatever may be the time displayed by a clock of S′ when the signal starts propagating along the x′ axis, this clock will have advanced by the time interval$\Delta t^{\prime }=L^{\prime }/c$ , after the signal has completely covered the ground distance L′. About the corresponding elapsed time of clock $O^{\ast }$ , we need to consider that, when co-moving in the lower part of the tube, clock $O^{\ast }$ is sharing the same properties of the clocks fixed to the x′ axis. Therefore, since for S’’clock $O^{\ast }$ is always co-moving with the lower part of the tube while the signal is propagating along this lower part, the time interval by which $O^{\ast }$ advances must be the same as that of any other clock of S′. It follows that, as inferred by S’’, the proper length $L^{\prime }={\gamma }^{\prime }L/\gamma$ must be covered by the signal in the time interval

   $\Delta t^{\prime }=\Delta t^{*}=\frac{L^{\prime }}{c}={\gamma }^{\prime }\frac{L}{\gamma c},$ (8)

as measured by clock O∗ or any other clock of S′.

S’’ can claim the above result to be a necessary consequence of the observed physical reality shown in Fig. 3, reflecting the simultaneity of the two events: signal at point B and clock $O^{\ast }$ at point A. For S’’, this reality requires that the signal has still to travel the ground distance $L^{\prime }={\gamma }^{\prime }L/\gamma$ at the ground speed c after the clock $L^{\prime }={\gamma }^{\prime }L/\gamma$ reaches point A and, therefore, result (8) must inevitably hold. Then, for$S^{″}$ , the total time $t_{+}^{\text{'}}=t_{+}^{*}$  displayed by clock $O^{\ast }$ for the clockwise signal propagation must be,

$t_{+}^{*}=t_B^{\text{'}\text{'}}+\Delta t^{\prime }=2\gamma \frac{L}{c}.$ (9)

For the counter-clockwise propagation, the result is the same. Therefore, the propagation time difference for the light signals is$\Delta t^{*}=t_{-}^{*}-t_{+}^{*}=0$ , and no Sagnac effect is foreseen if the local speed of the signal is $C^0=c$ everywhere along the tube.

b) The second argument that detractors of standard special relativity may point out are the following.

Let us suppose that in (9) we have$\Delta t^{\prime }\to \Delta t_{SR}^{\text{'}}=\gamma {\left(1-v/c\right)}^{2}L/c$ , in agreement with special relativity (see (4) and (5)) and experimental observation. Then, we may write

$t_{+}^{*}=t_B^{\text{'}\text{'}}+\Delta t_{SR}^{\text{'}}$ (10)

and, correspondingly,

$\frac{2\gamma L\left(1-v/c\right)}{c}=\frac{L/\gamma }{c}+\frac{{\gamma }^{\prime }L/\gamma }{\stackrel{⌢}{c}} ,$  (11)

where, on the lhs of (11), $2\gamma L$ is the total length covered by the signal, and c/(1−v/c) ≃c+v is the corresponding superluminal average speed. On the rhs of (11), the length L/γ of the first term represents the length covered by the signal in the upper part of the tube and $\stackrel{⌢}{c}$ the corresponding local speed. The length ${\gamma }^{\prime }L/\gamma$ in the second term represents the length covered by the signal in the lower part of the tube and $\stackrel{}{\overbrace{c}}$  the corresponding local speed. Simple algebra indicates that the local speed$c$ , in the lower part of the tube, must be $\stackrel{}{\overbrace{c}}\simeq \text{c}+2\text{v} ,$, i.e., superluminal, in contradiction with Einstein’s second postulate, as pointed out by Selleri. It follows that internal simultaneity, as assumed by both Newton and Einstein, is not compatible with the Lorentz transformations based on Einstein synchronization.

Physical reality and total time for the trip according to S′

We have shown in the previous section that, according to the physical reality of S’’, the local speed of light in the lower part of the tube, co-moving with S’, must be superluminal. In order to restore the local speed of light to c in this lower section of the tube, frame S’ has to synchronize clocks ("de-synchronize clocks", would argue a detractor) by means of Einstein synchronization, so that the LT can be used.

In this way, the physical reality of S’corresponds now to the reality of S’’changed, or "transformed", by means of the LT (6) as shown in Figure 4. It follows that, according to S’, simultaneity no longer holds because the signal reaches point B at the time

$t_B^{\text{'}}={\gamma }^{\prime }{t}_B^{\text{'}\text{'}}\left(1 - \frac{w}{c}\right)=\gamma \frac{L}{c}{\left(1 - \frac{v}{c}\right)}^2$

while clock $O^{\ast }$ reaches point A at the later time

$t_A^{\text{'}}=t_B^{\text{'}}+\delta t^{\prime }={\gamma }^{\prime }{t}_B^{\text{'}\text{'}}=\gamma \frac{L}{c}\left(1 + \frac{v^2}{c^2}\right)$

being

$\delta t^{\prime }=t_A^{\text{'}}-t_B^{\text{'}}={\gamma }^{\prime }{t}_B^{\text{'}\text{'}}\frac{w}{c}=2\gamma L\frac{v}{c^2},$ (12)

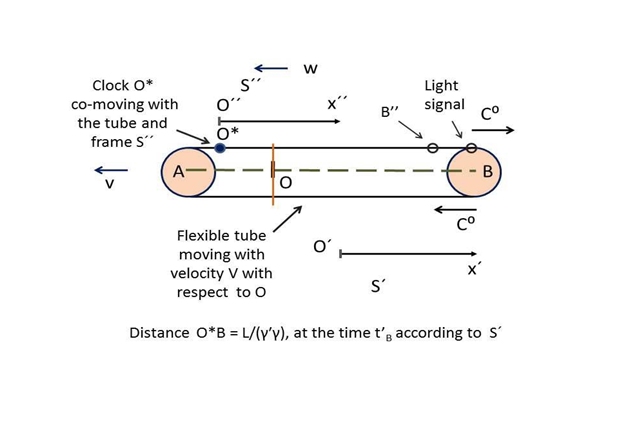
Figure 4 The linear Sagnac effect described from the perspective of frame S′ at the time $t_B^{\text{'}}$ . The origins O′′ and O′ were coinciding with the origin O at t = t′ = t′′= 0. At the time $t_B^{\text{'}}$ the signal has reached point B while clock O* has not yet reached point A. At time$t_B^{\text{'}}$ , the reading ofclock $O^{\ast }$ is$t_B^{\text{'}\text{'}}=t_B^{\text{'}}/{\gamma }^{\prime }<t_B^{\text{'}\text{'}}$ , while the proper ground length $O^{\ast }B$ is$L/\gamma$ . Hence, the corresponding ground speed is$\stackrel{}{\overbrace{c}}\simeq c+2v>c.$

the time interval (Kassner’s time gap) introduced by non-conservation of simultaneity. Fig. 4 pictures the physical reality of S’ at the time indicating that O∗ is at the distance $L/\gamma {\gamma }^{\prime }$ from B and at the distance $\Delta x^{\prime }=2\left(v^2/c^2\right)\gamma L/{\gamma }^{\prime }$ from A. The physical reality of S’ at the later time $t_A{}^{\prime }$ is pictured by Figure 5, indicating that when clock $O^{\ast }$ reaches A the signal has already traveled from B toward point A in the lower part of the tube during the time interval δt′ and is now at the shorter distance $L/\gamma -c\delta t^{\prime }$ from A and clock $O^{\ast }$ .  According to S’, as a consequence of

non-conservation of simultaneity the signal is not located at point B at the time$t_A^{\text{'}},$ , but has already moved in the lower part of the

tube from B toward $O^{\ast }$ by the amount $c\delta t^{\prime }=2\gamma L\left(v/c\right)$ , as shown in Figure 5. Meanwhile, in the same time interval $\delta t^{\prime }$ point A has moved with respect to O' by$-v\delta t^{\prime }$ . Thus, at the time $t_A{}^{\prime }$ , the remaining shorter distance to be covered by the signal is $L/\gamma -\left(c-v\right)\delta t$ ′, so that when the signal finally reaches $O^{\ast }$ this clock must have advanced by the time interval

$\Delta t_{SR}^{\text{'}}=\frac{L/\gamma -c\delta t^{\prime }+v\delta t^{\text{'}}}{c}=\frac{\gamma L}{c}{\left(1 - \frac{v}{c}\right)}^2.$  (13)

Then, according to S’, the total time displayed by clock O∗ at the end of the clockwise cycle is

$t_{+}^{*}=t_B^{\text{'}\text{'}}+\Delta t_{SR}^{\text{'}}=\frac{2\gamma L}{c}-\frac{2\gamma Lv}{c^2}=\frac{2L}{\gamma \left(c+v\right)},$  (14)

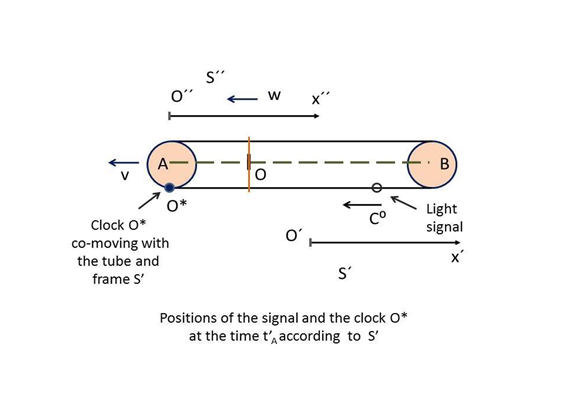
Figure 5 The linear Sagnac effect described from the perspective of frame S’ at the time $t_A^{\text{'}}$ . Clock $O^{\ast }$ has reached point A and, after turning around the pulley, starts co-moving with the lower part of the tube and frame S’. Because of the swifter ground speed $\stackrel{}{\overbrace{C}}>c$ in the upper part of the tube, the signal has already moved along the lower part of the tube advancing by $c\delta t^{\prime }$ from B toward $O^{\ast }$ .

In agreement with (10) and (11) as foreseen by special relativity. For the counterclockwise propagation, we find $t_{-}^{*}=2\gamma L\left(1-v/c\right)/c$  and thus, being $\Delta t^{*}=t_{-}^{*}-t_{+}^{*}=4\gamma Lv/c^2$  as in (5), the LT applied in frame S′ correctly foresee the Sagnac effect. It should be pointed out that the difference between (8) and (13) is precisely the time interval (12),$\delta t\text{' }=2\gamma Lv/c^2$  , introduced by non-conservation of simultaneity. As pointed out above, according to S′ and in agreement with standard special relativity, result (14) indicates that, for $C^0\Rightarrow c$ , the average counter-propagation speed, along the invariant ground length $2\gamma L$ of the closed path, is superluminal and given by $\simeq c+v$ .

Supporters of special relativity may claim that, although the average speed is superluminal, after Einstein synchronization the local speed in the lower part of the tube co-moving with S’is c, as it should be. Nevertheless, detractors of Einstein synchronization may argue that the local speed in the lower part of the tube has been achieved by re-setting the clocks in that part of the tube in such a way that the speed be c. For doing this, frame S’ has to pay a price because now the average superluminal speed $\simeq c+v$ along the closed path $2\gamma L$ cannot be justified by S’, unless the ground speed in the upper part of the tube is not only superluminal, but greater than the average value $\simeq c+v$ and of the order $\simeq c+2v$ . In fact, by synchronizing clocks with Einstein procedure, S’ has introduced the kinematical mechanism of non-conservation of simultaneity and the physical reality of $S’’$ has been changed. The resulting effect consists of modifying the time interval (8), making it shorter by a first order contribution in $v/c$ in order to equal the value (13). Because of non-conservation of simultaneity, when seen from the snapshot perspective of S’shown in Fig. 4, the clocks of S’’ in the upper part of the tube display readings predicted by the Lorentz time transformations. If the perspective of S’ is taken realistically (and is not a mere mathematical makeup), the reading of O*, at the time $t_B^{\text{'}}$ , can be inferred by means of the inverse Lorentz transformations, so that the time reading of clock O*

(at x′′ = 0) turns out to be

${\stackrel{}{\overbrace{t}}}_B^{\text{'}\text{'}}=\frac{t_B^{\text{'}}}{{\gamma }^{\prime }}=t_B^{\text{'}\text{'}}\left(1 - \frac{w}{c}\right)= \frac{L}{\gamma c}\left(1 - \frac{w}{c}\right).$ (15)

Obviously, the clock reading $t_B^{\text{'}\text{'}}$  represents the time of flight
of the signal from O* to the point of the tube reached by the signal at that time. According to S’’, at the time ${\stackrel{}{\overbrace{t}}}_B^{\text{'}\text{'}}$ the light signal has not yet reached point B but has covered only shorter ground length $L_{B^{″}}=c{\stackrel{⌢}{t}}_B^{\text{'}\text{'}}$  to the point B′′ shown in Fig. 4. For the Newtonian mindset, the fact that, at the displayed time ${\stackrel{}{\overbrace{t}}}_B^{\text{'}\text{'}}$ , the signal can be in two different places, at B or B′′, depending on the point of view of S’ or S’’, hints at an inconsistency between the two physical realities. However, if we admit non-conservation of simultaneity and focus on the reality of S’, it is a fact that, at the time$t_B^{\text{'}}$ , the signal has already reached point B, past B′′.

Thus, we may conclude that the signal has been sped up by non-conservation of simultaneity, while propagating in the upper section of the tube from clock O∗ to point B, past B′′. Considering that the ground length O*B is $L/\gamma$ and that ${\stackrel{}{\overbrace{t}}}_B^{\text{'}\text{'}}$  is the time of flight of the signal, we are compelled to infer that the local ground speedof the signal along O∗B is,

$\stackrel{}{\overbrace{c}}=\left(L/\gamma \right)/{\stackrel{}{\overbrace{t}}}_B^{\text{'}\text{'}}=c/\left(1-w/c\right)\simeq c+2v ,$  (16)

i.e., superluminal for$C^0=c$ , in conflict with the postulate of the constancy of c
In short, the argument discussed in b) in the above subsection, holds here also. If the average speed over the total length$2\gamma L$ is$\simeq c+v$ , and, over the partial length $\gamma L{\left(1-v/c\right)}^2$ of (13) in the lower part of the tube, the local speed is c, it follows that the local speed in the remaining part must be$\simeq c+2v$ , i.e., superluminal.

Preliminary conclusions

The two physical realities of Figure 3 (for S’’) and Figure 4 (for S’) are physically incompatible and lead to different results and interpretations of the Sagnac effect. For both Newton and Einstein, in an inertial reference frame the physical reality is described synchronously, i.e., at the same simultaneous time in every point of space of the inertial frame. The contrasting results obtained by S’’ and S’((9) and (14), respectively) are simply the reflection of the incompatibility between the concept of simultaneity and Einstein’s concept of relative time.

Non-conservation of simultaneity and the Lorentz transformations are direct consequences of Einstein synchronization and the validity of the second postulate of special relativity. Detractors of Einstein synchronization may claim that the resulting average propagation speed $\simeq c+v$ of (14) implies signal propagation at a superluminal local ground speed along some section of the closed path, in line with Selleri’s paradox for the circular Sagnac effect. We have shown that, for the equivalent linear Sagnac effect, if in one of the inertial frames, S’’or S’, the local ground speed is c, the local speed in the other inertial frame must be superluminal and of the order of$\simeq c+2v,$ , in contrast with Einstein’s second postulate. This result is seen as reflecting the incompatibility of Einstein synchronization applied to the closed path of the Sagnac effect, even when applied separately to the upper and lower parts of the tube. Therefore, since Einstein synchronization implies the existence of superluminal local speeds, the second postulate of SR is invalid.

Nevertheless, thinking beyond the controversy about the validity of the postulate of the universal light speed c in all inertial systems, supporters of SR may shift the debate to a more pragmatic scenario by highlighting the correctness of the predictions of the theory. They could argue that, even though the second postulate of SR is questionable because of the superluminal speeds involved in the interpretation of the Sagnac effect, from an operational standpoint, Einstein synchronization can still be applied to the upper and lower parts of the tube. Therefore, from a pragmatic point of view, followers of standard special relativity may claim that the theory is sound because, by means of non-conservation of simultaneity, it predicts for the Sagnac effect the observed results, derived either in the laboratory frame S or in the tube co-moving frame S’’or S’. Along these lines, assuming the physical equivalence between absolute and Einstein synchronization, Kassner argues that the difference between a local speed c and a superluminal average or local speed$\simeq c+v$ is to be interpreted in terms of the arbitrariness of synchronization and, thus, does not invalidate the second postulate of special relativity.

Thus, the debate of relative versus absolute time is at a standstill and it is unlikely that historically long debates such as this can be settled through mere theoretical arguments. Fortunately, physicists agree that, if there is a meaningful difference between opposing points of view, it must be ultimately observable, i.e., experimentally testable. Therefore, the best clear-cut way to solve the controversy is by means of a test capable of discriminating absolute versus Einstein synchronization. As shown in the next section, such a test exists and is precisely the Sagnac effect.

Regardless of the feasibility or not of experimental verification, the mere existence in principle of such a test proves that the Lorentz transformations are not physically equivalent to transformations based on absolute synchronization. An immediate consequence is that it is conceptually unfeasible to use the Tangherlini transformations and absolute synchronization in trying to conciliate, as claimed by Kassner, the superluminal average speed of the Sagnac effect with the postulate of the constancy of the speed of light. In principle, the two synchronizations are physically distinguishable and the arbitrariness of synchronization can no longer be invoked to substitute the LT with the TT in order to explain Selleri’s paradox, which remains unsolved.

Non-equivalence of Einstein and absolute synchronization

In relativistic theories, the coordinate transformations between inertial frames of reference in relative motion may take into account the synchronization procedure adopted (for example, internal and external ) through the dependence of the time ton a convenient synchronization parameter ε. The contention of conventionalism is that clock synchronization is arbitrary and, thus, the one-way speed of light, that can be expressed as$c(\epsilon )$ , is conventional and not measurable in principle. It follows that, within this scenario, an observable quantity must be synchronization-independent in order to be physically meaningful. If the observable quantities of relativistic theories are independent of the chosen synchronization procedure, all the experiments supporting standard special relativity also support a preferred frame theory with absolute synchronization. Then, non-conservation of simultaneity, which is a consequence of Einstein synchronization procedure, should not be observable per se. If, instead, synchronization is not arbitrary, it is feasible that some observable quantities are dependent on synchronization and, thus, their measurement would allow for the determination of the "natural" synchronization that fits with observation. In the case of the Sagnac effect, the propagation times over a cycle are measured by means of a single clock and there is no need to perform synchronization of distant, spatially separated clocks. If the laboratory frame S is chosen as the preferred frame where space is isotropic, the time relation t*= t/γ between clock O^∗ in motion with relative velocity v and a clock stationary in Sis the same for TT and LT. Therefore, both theories foresee the same results, independent of ε. However, it is unlikely that the laboratory where the Sagnac experiment is performed, located somewhere on the rotating Earth, should coincide with the preferred frame of some ether theory. Thus, it is justified to consider the hypothetical case when, in frame S, space is no longer isotropic, as a consequence of its possible motion with respect to some preferred frame. Let us then envision the existence of the preferred inertial frame $\Sigma \left(X,T\right)$ where space is isotropic and the one-way speed of light is c. In the Figure 2 we have to suppose that the laboratory frame S, where the set-up (arm AB) of the linear Sagnac effect is stationary, moves with velocity Win the Xdirection with respect to Σ. The clock $O^{\ast }$ , co-moving with frame S′, has velocity $W^{\prime }$ with respect to Σ. The following transformations⁸ apply to relativistic theories (special relativity with arbitrary synchronization parameter ε):

$x={\gamma }_W\left(X-WT\right);y=Y;z=Z$

$t={\gamma }_W\left[T\left(1+\frac{W^2}{c^2}\left(\epsilon -1\right)\right)-\epsilon \frac{WX}{c^2}\right]$  (17)

In Equation (17), when $\epsilon =1$ we recover the time relation $t={\gamma }_W\left(T-WX/c^2\right)$ of the LT and, when$\epsilon =0$ , the relation$t=T/{\gamma }_W$ of the TT. After taking the derivative$dx/dt$ , for the components of the velocity in the x, X direction, we obtain from (17),

$u=\frac{U-W}{\left(1+\frac{W^2}{c^2}\left(\epsilon -1\right)\right)-\epsilon \frac{WU}{c^2}}$ (18)

$v=\frac{W^{\prime }-W}{1+\frac{W^2}{c^2}\left(\epsilon -1\right)-\epsilon \frac{W{W}^{\prime }}{c^2}}$  (19)

We can see that for the $LT(\epsilon =1)$ the velocity composition (19) gives, as expected, $v=\left(W^{\prime }-W\right)/\left(1-W^{\prime }W/c^2\right)$ , while for the $TT(\epsilon =0)$ we have$v={\gamma }_W^2\left(W^{\prime }-W\right)$ . Expressed in terms of Wand v, the velocities of S′ and S′′ with respect to Σ are respectively,

$W^{\prime }=\frac{W+v\left[1+\frac{W^2}{c^2}\left(\epsilon -1\right)\right]}{1+\epsilon \frac{vW}{c^2}}$ ; $W^{\text{'}\text{'}}=\frac{W-v\left[1+\frac{W^2}{c^2}\left(\epsilon -1\right)\right]}{1-\epsilon \frac{vW}{c^2}}$  (20)

The following results, which depend on ε, are obtained for the linear Sagnac effect. As measured in the preferred frame Σ, the time intervals for the counter-propagating signal (clockwise propagation in Figure 2) with one-way speed c from A to B and from B to$O^{\ast }$ are respectively:

$T_{AB}=\frac{L}{\left(c-W\right){\gamma }_W};T_{B{O}^{*}}=\frac{L}{\left(c+W^{\prime }\right){\gamma }_W}-\frac{W^{\prime }-W}{c+W^{\prime }}{T}_{AB}$ .

The time T+ for counter-propagation and T− for co-propagation turns out to be, respectively,

$T_{+}=T_{AB}+T_{B{O}^{*}}=\frac{2L}{c\left(1+W^{\prime }/c\right)\left(1-W/c\right){\gamma }_W}$

$T_{-}=\frac{2L}{c\left(1-W^{\prime }/c\right)\left(1+W/c\right){\gamma }_W}$

$\Delta T=T_{-}-T_{+}=\frac{4L}{c^2}{\gamma }_{W^{\prime }}^2{\gamma }_W\left(W^{\prime }-W\right)$ (21)

where $\Delta T$ is the time span difference. The corresponding time difference $\Delta t^{\prime }$ measured by the clock $O^{\ast }$  for the Sagnac effect is,

$\Delta t^{\prime }=\Delta t^{*}=\frac{\Delta T}{{\gamma }_{W^{\prime }}}=\frac{4L}{c^2}{\gamma }_{W^{\prime }}{\gamma }_W\left(W^{\prime }-W\right)$ (22)

By means of (20), we may substitute in (22) W ′ expressed in terms of Wand $v$ and obtain,

$\Delta t^{\prime }=\frac{4Lv}{c^2{\gamma }_W}{\left\{{\left(1+\epsilon \frac{vW}{c^2}\right)}^2-{\left(\frac{W}{c}+\frac{v}{c}\left[1+\frac{W^2\left(\epsilon -1\right)}{c^2}\right]\right)}^2\right\}}^{-1/2}.$ (23)

Result (23) indicates that the optical path difference for two counter-propagating electromagnetic waves depends on the synchronization parameter ε in the Sagnac effect. If the procedure

used above is applied to other optical tests, for example, to the Michelson-Morley experiment, we find instead that ∆t′ is independent of ε, as also shown by Mansouri and Sexl.

If we set $\epsilon =1$ in (23), the term ${\left\{\mathrm{...}\right\}}^{-1/2}$ becomes γWγ and as foreseen by the LT, we obtain $\Delta t^{\prime }=4\gamma Lv/c^2$ independent of W. Withε=0 , the coupled term vW/c² does not vanish and, being attributable to the absolute synchronization, is present also in the Newtonian case. Thus, for the TT, from (23) we obtain,

$\Delta t^{\prime }=\Delta t^{*}=\frac{4Lv}{c^2}{\left[{\left(1 - \frac{vW}{c^2}\right)}^2- \frac{v^2}{c^2}\right]}^{-1/2}$ (24)

To the order$vW/c^2$ and with${\gamma }^{-2}=1-v^2/c^2$ , the term [...]−1/2 in(24) becomes,

${[\dots ]}^{-1/2}\simeq {[{\gamma }^{-2}-2\frac{vW}{c^2}]}^{-1/2}\simeq \gamma \left(1+\frac{vW}{c^2}\right)$ (25)

When, after reaching point B, the clock O∗ changes direction and moves with velocity −v with respect to S, the relation $W^{\prime }=W+v/{\gamma }_W^2$ has to be replaced by$W^{″}=W-v/{\gamma }_W^2$ , while the factor ${\gamma }_{W^{\prime }}$ has to be replaced by ${\gamma }_{W^{″}}$ in the

calculations. Furthermore, instead of the time interval ∆t′ = ∆t∗, we have now ∆t′′ = ∆t∗, which is the same as the expression ∆t′ of (24) with the term −vW/c2 replaced by +vW/c2.

Result (24) can be immediately extended to the circular Sagnac effect, where the clock moves with tangential speed $v=\omega R$ and its x-component is$v_x=vcos(\omega t)$ , by writing $\pm vW/c^2\Rightarrow \left(vW/c^2\right)cos(\omega t).$ Then, with the help of (25), the time span (24) measured by clock $O^{\ast }$ in the Sagnac effect can be expressed as

$\Delta t^{*}\simeq \frac{4\gamma Lv}{c^2}\left[1+\frac{vW}{c^2}\cos \left(\omega t\right)\right]$ (26)

Precision measurements of (26) can provide the value of the component W of the absolute velocity of the laboratory frame with respect to Σ.

Concerning the smallest measurable time interval, there are techniques capable of resolving femtosecond (${10}^{-15}\left(s\right)$ ) [45] or even attosecond (${10}^{-18}\left(s\right)$ )^46,47 pulses of laser light while better limits may be achieved by means of advanced interferometer. In terms of phase shift, we may write $\Delta \phi =c\Delta t^{\ast }/(\gamma \lambda )$ where λis the vacuum wavelength and c is the free-space velocity of light [30]. Then, result (26) can be expressed as

$\Delta \phi \simeq \frac{4Lv}{\lambda c}\left[1+\frac{vW}{c^2}\cos \cos \left(\omega t\right)\right]=K\left[1+A\cos \left(\omega t\right)\right]$ (27)

The amplitude Ain (27) could be more easily measured if interferometer techniques were available where the constant amplitude K is locked and fixed and we could estimate Wby resolving the relative fluctuation proportional to A=vW/c² and alternating with frequency ω. In any case, the stability of the amplitude K, is probably the limiting factor in any such possible experiment because the inevitable vibrations of the table or pillar on which the experiment is mounted will be hard to cancel out altogether. Therefore, the "constant" Kwill have its own fluctuations which can exceed A. Hopefully, we can transfer some of the advanced techniques developed for gravitational wave detection,⁴⁹ to the scenario of our experiment. There are vibration cancellation schemes available for wave interferometers, although very expensive. The phase measuring gravity wave detectors (which are the best in this category) keep Knear zero and, in special conditions by various enhancement techniques, one can theoretically hope for 10−9−10−11 of a fringe. Sometimes adding an optical cavity multiplies the signal by factor of 10².

Already at the time of Sagnac, for similar experiments [30, 49-50] the fringe shift was$\Delta \phi \simeq K\simeq 1$ . With this value for Kin (27) and with an optimal resolution of 10⁻¹³ of a fringe, requiring a lot of work and money, we can get an idea of the value of W that can be detected in some experimental conditions. Assuming that the smallest detectable value of $A=vW/c^2$ is${10}^{-13}$ , with a velocity $v\simeq 450\left(m/s\right)$ (a value of the order of the tangential speed of the Earth at the equator), we have $W={10}^{-13}{c}^2/v\simeq 20\left(m/s\right)$ as the minimum absolute velocity W detectable. Historically, the velocity W with respect to the preferred frame has been expected to be that of the Earth’s orbital speed$(W\simeq 30\left(km/s\right)$ , in relation to the Michelson-Morley experiment) or the absolute speed of the Earth through space$(W\simeq 300\left(km/s\right)$ , in relation to the observed cosmic background-radiation anisotropy). Therefore, we could hope to verify these two assumptions and even check if the hypothetical preferred frame is identifiable with the inertial rest frame of the center of the Earth$(W\simeq 450\left(m/s\right))$ . Although the realization and the cost of the experiment are certainly quite challenging factors, we believe this test not to be completely outside the reach of present technology. We may conclude that the two synchronizations (Einstein and absolute) are not physically equivalent in principle, but almost equivalent in practice and, should experimental evidence favor the absolute synchronization, it is understandable why experimental discrepancies with Einstein synchronization have not been evidenced so far. In this case, we may state that, from an operational perspective, Einstein synchronization represents a useful simple approach to the procedure of clock synchronization, capable of reproducing approximately the results of relativistic theories based on absolute synchronization.

Nevertheless, we will show in a future contribution that, with a modified experiment of the Sagnac type, the variation in which should be more easily measurable.

Consequences of the non-equivalence of Einstein and absolute synchronization

In the case of the Michelson-Morley experiment, the observed null result rules out the Galileo transformations, which foresee a non-null outcome. Instead, the TT and LT are confirmed because both predict the observed null result. In the case of the Sagnac effect, the non-null result $W=0$ would confirm absolute synchronization, i.e., Galileo transformation and the TT, while disproving standard SR. If the experimental result indicates that$W=0$ , the conclusion that can be drawn is the same as that of the Michelson-Morley experiment: the preferred frame coincides with the laboratory frame Sand both LT and TT are confirmed. However, it would be a conceptual error to conclude that they are equivalent, after having shown above that in principle they are physically distinguishable. A conclusive experimental proof consists of repeating the experiment having the Sagnac apparatus in motion with respect to S, identified as the preferred frame by the first experiment. Regardless of experimental verification, the mere existence in principle of such a test proves that absolute and Einstein synchronization are not physically equivalent. Even if the outcome of the experiment indicates the existence of a preferred frame of reference, the principle of relativity of physical laws holds. However, in this case, the principle has to reflect the invariance under transformations adopting absolute synchronization.

In conclusion, the countless theoretical approaches to modern physics based on the Lorentz covariance are substantially different from, and cannot be equivalently substituted by, approaches based on the invariance of physical laws under the TT. Therefore, it is conceptually unfeasible to use the Tangherlini transformations in trying to conciliate, as claimed by Kassner, the superluminal average speed of the Sagnac effect with the postulate of the constancy of the speed of light by invoking the arbitrariness of synchronization.

The thesis of conventionalism is based on the assumption that clock synchronization is arbitrary, so that the one-way speed of light is conventional and not measurable. Accordingly, Einstein’s second postulate of special relativity, requiring a universal light speed c in all inertial frames of reference, is not falsifiable. Consequently, all the experiments supporting special relativity can be interpreted in terms of the Lorentz transformations based on Einstein synchronization, as well as the physically equivalent Tangherlini transformations based on absolute synchronization. This scenario implies that the Lorentz transformations can be substituted by the Tangherlini transformations, a substitution hardly acceptable by physicists who have been relying on the symmetry of the Lorentz group for decades.

For the Sagnac effect, where light signals propagate in a closed path, for counter-clockwise light propagation, relativistic theories foresee the superluminal average speed$\simeq c+v$ , a well-known circumstance that leads to Selleri’s paradox and, according to detractors of SR, invalidates Einstein’s second postulate. The analysis of the "linear" Sagnac effect points out the role of non-conservation of simultaneity in keeping the local speed c in different sections of the tube when Einstein synchronization is used. Since the superluminal average speed is $\simeq c+v$ over the total length $2\gamma L$ of the tube, if in the upper part of the tube clocks are synchronized in such a way that the local speed is c, it follows that in the lower part of the tube the local speed must be$\simeq c+2v$ , and vice versa. Thus, detractors of SR may claim once more that the existence of superluminal light speeds invalidates Einstein’s second postulate. Despite Selleri’s paradox and superluminal average speeds, supporters of Einstein synchronization may argue that special relativity provides the correct observable result for the Sagnac effect and, thus, is still valid from a pragmatic operational point of view.

The controversy about the conventionality of the one-way speed of light and the validity or not of Einstein synchronization, reaches a turning point when it is shown that the second postulate of SR can be tested with an experiment of the Sagnac type, capable of discriminating absolute from Einstein synchronization. Hence, Einstein’s second postulate is falsifiable and the one-way speed of light is measurable in principle. From a theoretical point of view, an immediate consequence is that the symmetry of the Lorentz group maintains its unique physical meaning and cannot be equivalently substituted by the group properties of transformations based on absolute synchronization. Moreover, the claim that the existence of superluminal speeds in the Sagnac effect can be justified in terms of the arbitrariness of synchronization becomes groundless.

The experiment is realizable with present technology and the required sensitivity of the measuring apparatus is evaluated in some scenarios. The outcome of the test will have a significant impact on modern physics because, by testing Einstein’s postulate of a universal speed of light, it identifies, or rules out, the preferred frame of reference.

This work was supported in part by the CDCHTA of the Universidad de Los Andes, Mérida, Venezuela.

Authors declare that there are no conflicts of interests.

1. Krisher TP, Lute Maleki, George F Lutes, et al. (1990) Test of the isotropy of the one-way speed of light using hydrogen-maser frequency standards. Phys Rev D. 1990;42:731.
2. Spavieri G, Quintero J, CS Unnikrishnan, et al. Can the one-way speed of light be used for detection of violations of the relativity principle? Phys Lett A. 2012;376:795–797.
3. H Poincare. Létat Actuel Et l'avenir de la physique mathématique; Parm Henri Poincaré. Bulletin des Sciences Mathématiques. 1994;28:302–324.
4. A Einstein. Einstein’s Miraculous Year. Princeton University Press, New Jersey, USA. 1998.
5. R Reichenbach. Axiomatization of the Theory of Relativity. University of California Press 1st edn. (1924) & The philosophy of Space and Time. Dover (1st German edn.) (1928). 1969.
6. Grunbaum. Philosophical Problems in Space and Time 1st edn. Cambridge Univ. Press, Cambridge, USA. 1973.
7. C Moller. The Theory of Relativity. Suppl Nuovo Cimento. 1957;(6):381.
8. R Mansouri, RU Sexl. A test theory of special relativity: I. Simultaneity and clock synchronization. Gen Rel Grav. 1977;8(7): 497–513.
9. FR Tangherlini. The Tangherlini transformations are known in the literature also as the IST 20(1) transformations and (2015) The Selleri transformations and the one-way speed of light by Stephan JG Gift. 1961;28:474–481.
10. JS Bell. Speakable and Unspeakable in Quantum Mechanics 2nd edn. Cambridge Univ. Press, Cambridge, USA. 1988.
11. R de Abreu, V Guerra. Thought experiment discriminating special relativity from preferred frame theories. Eur J Phys. 2005;26:117–123.
12. Vasco Guerra, Rodrigo de Abreu. On the Consistency between the Assumption of a Special System of Reference and Special Relativity. Foundation Physics. 2006;36(12):1826–1845.
13. R de Abreu, V Guerra. Special relativity as a simple geometry problem. Eur J Phys. 2008;29:33–52.
14. F Selleri. The Inertial Transformations and the Relativity Principle. Foundations of Physics Letters. 2005;18(4):325–339.
15. B Ellisv, P Bowman. Conventionality in Distant Simultaneity. Philosophy of Science. 1967;34:116–136.
16. RW Brehme. The role of dynamics in the synchronization problem. American Journal of Physics. 2004;72(2):56–59.
17. R Anderson, I Vetharaniam, GE Stedman. Conventionality of synchronisation, gauge dependence and test theories of relativity. Physics Reports. 1988;295(3):93–180.
18. MM Capria. On the Conventionality of Simultaneity in Special Relativity. Foundation Physics. 2001;31(5):775–818.
19. HC Ohanian. The role of dynamics in the synchronization problem. American Journal of Physics. 2004;72:141–148.
20. G Spavieri. On measuring the one-way speed of light. The European Physical Journal D. 2012;66:76.
21. G Sagnac.Sagnac effect in an off-center rotating ring frame of reference. CR Acad Sci English translation in Relativity in rotating frames, chap 2nd ed. Rizzi G & Ruggiero ML Kluwer Academic Publishers, Dordrecht, Netherlands. 2004;1913; p. 5–7.
22. K Kassner. Ways to resolve Selleri's paradox. American Journal of Physics. 2012;80(12):1061.
23. F Selleri. Noninvariant one-way speed of light and locally equivalent reference frames. Foundations of Physics Letters. 1997;10(1):73–83.
24. F Selleri. Recovering the Lorentz Ether. Apeiron. 2004;11(1):246–281.
25. KR Atkins. Lorentz ether theory versus relativity — The possibility of new experimental evidence. Phys Lett A. 1980;80(4):243–245.
26. M Consoli, E Costanzo. From classical to modern ether-drift experiments: the narrow window for a preferred frame. Phys Lett A. 2004;361(6):509–512.
27. M Consoli, E Costanzo. Reply to:Comment on: From classical to modern ether-drift experiments: the narrow window for a preferred frame. Phys Lett A. 2007;361:513–514.
28. G Spavieri. On measuring the one-way speed of light. 2012;66:76.
29. Hafele C, Keating RE. Around-the-World Atomic Clocks: Predicted Relativistic Time Gains. Science. 1972;177(4044):166–170.
30. R Wang, Y Zhengb, A Yaob, et al. Modified Sagnac experiment for measuring travel-time difference between counter-propagating light beams in a uniformly moving fiber. Physics Letters A. 2012;312:7–10.
31. EJ Post. Sagnac Effect. Review of Modern Physics. 1967;39(2):475–493.
32. LD Landau, EM Lifshitz. Teoriya Polya. The Classical Theory of Fields. Oxford: Pergamon Press. 1967.
33. VI Bashkov, V Sintsova Yu. Connections in Principal Bundles and the Sagnac Effect , Grav. Cosmology. 1999;5:319–320.
34. VI Bashkov, V Sintsova Yu. Rep Math Phys. 2001;48:353.
35. VI Bashkov, M Malakhaltsev. In Intern Conf “Geometrization of Physics V”. 2001. p. 24–28.
36. NV Kupryaev. Izv Vyssh Uchebn. Zave Fiz. 1999;42(7):8.
37. NV Kupryaev. Izvestiya Vysshikh Uchebnykh Zavedenii. Matematika. 2001;44(8):63.
38. NV Kupryaev. The Sagnac Vortex Optical Effect. Russian Physics Jornal. 2001;44(8):858–862.
39. GB Malykin. Sagnac effect in a rotating frame of reference. Relativistic Zeno paradox. Physics-Uspekhi. 2002;45(8):907–909.
40. TA Weber. Measurements on a rotating frame in relativity, and the Wilson and Wilson experiment. American Journal of Physics. 1997;65: 946–953.
41. J Anandan. Sagnac effect in relativistic and nonrelativistic physics. Physical Review D. 1981;24:338–346.
42. SJG Gift. On the Selleri Transformations: Analysis of Recent Attempts by Kassner to Resolve Selleri’s Paradox. Applied Physics Research. 2015;7(2):112–120.
43. N Ashby. Relativity in the Global Positioning System. Living Reviews in Relativity. 2003;6(1):1–42.
44. F Selleri. Relativity in Rotating Frames. In: G Rizzi & ML Ruggiero editors. Kluwer Academic Publishers, London. 2010.
45. SJG Gift. One-Way Speed of Light Relative to a Moving Observer. Applied Physics Research. 2013;5(1):93–106.
46. DA Ludlow, MM Boyd, J Ye, et al. Optical atomic clocks. Reviews Modern Physics. 2015;87:637.
47. Kim J, Chen J, Cox J, et al. Attosecond-resolution timing jitter characterization of free-running mode-locked lasers. Optics Letters. 2007;32(24):3519–3521.
48. Kwon D, Jeon CG, J Shin, et al. BMP2-modified injectable hydrogel for osteogenic differentiation of human periodontal ligament stem cells. Scientific Reports. 2007.
49.  Abbott BP. Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters. 2016;116(6):061102.
50. Pogany B. Über die Wiederholung des Harress‐Sagnacschen Versuches. Ann Physik. 1928;385(11):217–231.
51. Pogany B. Über die Wiederholung des Harressschen Versuches. Ann Physik. 1928;390(2):244–256.