This paper deals with the planar circular restricted three-body problem when both the primaries are sources of radiation and oblate spheroids with their equatorial planes coincident with the plane of motion. A new mean motion is utilized which includes the secular effects of the oblateness of the primary on mean anomaly (M), the argument of perigee (ω), and right ascension of ascending node (Ω).¹ The value of the critical mass ratio (μ_c) is obtained in the series form. It is found that it further decreases with the increase in oblateness of the primaries as well with their radiation effect. The angular frequencies of the long-periodic orbits (s₄) and short-periodic orbits (s₅) around the triangular Lagrangian point (L₄) are computed in series form. It is observed that (s₄) increases with mass ratio μ, oblateness, and radiation pressure of both the primaries, while (s₅) decreases with mass ratio, oblateness, and radiation pressure of both the primaries. The eccentricities are also computed in the series form. It is observed that the eccentricity of long-periodic orbits (e₄) decreases with mass ratio, oblateness, and radiation pressure of both the primaries, whereas the eccentricity of short-periodic orbits (e₅) increases with mass ratio, oblateness, and radiation pressure of both the primaries. These results are confirmed with the numerical values. Comparisons of these solutions are made with the results of Singh and Ishwar² Abouelmagd and El-Shaboury,³ Arohan and Sharma,⁴ and Jency et al.⁵

Keywords: Restricted Three Body Problem, Oblateness, Radiation Pressure, Perturbations, Equilateral Points, Critical mass ratio, Periodic Orbits, Angular Frequencies, Eccentricities, Time Periods.

MB, Mitochondrial diseases; mtDNA, mitochondrial DNA; MRI, magnetic resonance imaging; GTCS, generalized tonic-clonic seizure; HSV, herpes simplex virus; ENMG, electroneuromyography

From Newton to Lagrange, the restricted three-body problem caught the curiosity of many mathematicians and astronomers in the early days of its development. The applications of the restricted three-body problem to celestial mechanics have formed the basis of certain lunar and planetary theories in recent years, with the launch of artificial satellites in the Earth-Moon system and in the solar system. Euler was the first to contribute to the restricted three-body problem in 1772. The theory of restricted three-body problem begins with Euler and Lagrange in 1772 and continues with Jacobi in 1836, Hill in 1878, Brown in 1896, Poincare in 1892, Levi-Civita in 1904, Birkoff in 1915, and many more current mathematicians and astronomers.⁶ Two bodies of masses m₁ and m₂ revolve around their centre of mass (barycentre) in circular orbits under the influence of their mutual gravitational attraction and a third body of mass m₃ attracted by the previous two bodies moves in a plane defined by the two revolving bodies. Here, the other two bodies are considerably having more mass than the third body (the mass of the third body is considered to be negligible and not in comparable with the other two heavier bodies). Since, the mass of the third body is restricted here; it will not influence the motion of other two revolving bodies. The two revolving bodies are called the primaries; they are also called as massive and smaller primaries, in accordance with their masses. The restricted three-body problem is to study the motion of third body around the primaries.

Sharma and Subba Rao^7-9 studied the restricted three-body problem by considering the more massive primary as an oblate spheroid with its equatorial plane coincident with the plane of motion by considering the secular effect of oblateness on mean motion.¹⁰ Sharma¹¹ studies the restricted three-body problem by considering the more massive primary as an oblate spheroid as well as source of radiation. Sharma¹² studies the restricted three-body problem by considering the more massive primary as a source of radiation and smaller primary as an oblate spheroid. Both the above studies used the mean motion of Subba Rao and Sharma.¹⁰ Many more studies were done with this mean motion expression literature.

Singh and Ishwar² studied the effect of oblateness and radiation pressure of both the primaries on the location and linear stability of the triangular points in the restricted three-body problem using the above mean motion expression. They derived a series expression for critical mass μ_c. Subba Rao and Sharma¹³ studied the effect of oblateness of the more massive primary on the non-linear stability of L₄ in the restricted three-body problem.

AbdulRaheem and Singh¹⁴ studied the combined effects of perturbations on the stability of equilibrium points in the restricted three-body problem. They investigated the perturbations due to small Coriolis and centrifugal forces, as well as the effects of oblateness and radiation pressure of the primaries for the equilibrium points. They calculated the critical mass by including all the perturbations. AbdulRaheem and Singh¹⁵ studied the effects of radiation and oblateness on the periodic orbits in the restricted three-body problem. Effect of Coriolis and centrifugal forces was also considered. Abouelmagd and El-Shaboury³ analyzed the periodic orbits under the combined effect of oblateness of three bodies and radiation pressure of both the primaries in circular restricted three-body problem. They calculated and plotted the variations of angular frequencies for perturbed and unperturbed cases with the mass ratio. Abouelmagd¹⁶ studied the linear stability of the triangular points with oblateness and radiation pressure in the restricted three-body problem. A series expression for critical mass μ_c is found. Ansari and Alam¹⁷ studied the circular restricted three body problem by considering one of the primaries as oblate and other one having the solar radiation pressure and all the masses are variable. They found that all the equilibrium points are linearly unstable. Khalifa¹⁸ carried out a semi-analytical study of the effect of ground-based laser radiation pressure on the location of triangular points in the framework of the planar circular restricted three-body problem. Jency et al.⁵ studied the stationary solutions, critical mass, tadpole orbits in the circular restricted three-body problem, where the massive primary is considered as an oblate spheroid. The authors utilized the new mean motion which included the secular effects of the oblateness of the primary on mean anomaly (M), the argument of perigee (ω), and right ascension of ascending node (Ω).¹ They found the critical mass value μ_c to decrease further, which was compared with the μ_c value obtained by Subba Rao and Sharma.¹⁰ They further calculated the angular frequencies of long- and short-periodic orbits. They also computed the angle between the two coordinate systems.

Arohan and Sharma⁴ utilized the new mean motion expression to study the stationary solutions of the planar circular restricted three-body problem when the more massive primary is a source of radiation and the smaller primary is an oblate spheroid with its equatorial plane coincident with the plane of motion. Locations of the Lagrangian points were found and an expression   for critical mass μ_c was obtained in the series form.  John and Sharma¹⁹ studied the circular restricted three body problem by considering with the more massive primary as an oblate spheroid and source of radiation by using the new mean motion expression.  The locations of the collinear Lagrangian points are found. The variations of the location of the Lagrangian points due to the unperturbed as well as the perturbed problem due to oblateness and radiation pressure were studied. A study on the eccentricity e and angular frequency s at the collinear points was carried out. Kumar et al.²⁰ utilized the new mean motion by considering both the primaries as oblate spheroids with their equatorial planes coincident with the plane of motion. They studied the stability of the equilibrium points and observed that the collinear equilibrium points are always unstable. However, the non-collinear equilibrium points are stable for some combinations of the involved parameters. They plotted the zero velocity curves of the infinitesimal body for different values of the Jacobi constant C and oblateness parameters. It was observed that the value of C played a vital role in obtaining the permissible regions of motion of the infinitesimal body.

In our study, we have considered both the primaries as oblate spheroids and source of radiation in the planar circular restricted three-body problem. We have utilized the newly derived mean motion by Sharma et al.¹ We have studied the effects of oblateness and radiation pressure of both the primaries on the critical mass ratio μ_c. We have also studied the variations of angular frequencies of long- and short periodic orbits at L₄ with mass ratio μ. We have further studied the variation of eccentricities and time periods of long- and short periodic orbits around L₄ with mass ratio. We have also generated an expression in series form for the angle α between the fixed and rotating coordinate system at L₄.  We have compared our results with other authors wherever possible. There are few new results in our study.

Equations of motion

We consider the two bodies called primaries of larger mass (m₁) and smaller mass (m₂) moving about their centre of mass in circular orbits in a plane (Figure 1). The third body of infinitesimal mass at point (P), which does not affect the motion of m₁ and m₂, is moving under their gravitational influence in the same plane. The origin of the system lies on the barycentre (centre of mass) of the primaries. r₁ and r₂ are the distances of the third body P from the more massive (m₁) and the smaller (m₂) primaries, respectively.

The equations of motion are given as

$\ddot{x}-2\mathrm{n}\dot{y}=\frac{\partial \text{Ω}}{\partial \text{x}}$   (1)

$\ddot{y}-2\mathrm{n}\dot{x}=\frac{\partial \text{Ω}}{\partial \text{y}}$   (2)

The force function Ω is given by:

$\text{Ω}=\frac{{\text{n}}^2\left({\text{x}}^2+{\text{ y}}^2\right)}{2}+\frac{{\text{q}}_1\left(1-\text{μ}\right)}{{\text{r}}_1}+\frac{{\text{q}}_2\text{μ}}{{\text{r}}_2}+\frac{{\text{A}}_1{\text{q}}_1\left(1-\text{μ}\right)}{2{\text{r}}_1{}^3}+\frac{{\text{A}}_2{\text{q}}_2\text{μ}}{2{\text{r}}_2{}^3}$ ,  (3)

where q₁ and q₂ are the mass reduction factors with respect to m₁ and m₂, constant for the particle, with q_i=1 – ε_i(i = 1, 2).ε_i are the ratio of radiation pressure forces to the gravitational forces [i.e., ε_i = F_Pi/F_gi].${\mu }_1 = \frac{\text{m}1}{\text{m}1+\text{m}2}, {\mu }_2 =\frac{\text{m}2}{\text{m}1+\text{m}2}$  ,are the mass ratios for the two masses (m₁) and (m₂), respectively.μ₁+ μ₂ = 1, If μ₂ = μ, then μ₁ = 1 – μ,  A_i = (AE_i² –AP_i²)/5R², (i =1, 2). AE₁ and AE₂ are the equatorial radii of the more massive and smaller primary, respectively. AP₁ and AP₂ are the polar radii of the more massive and smaller primary, respectively. R is the distance between the primaries. A₁ and A₂ are oblateness coefficients of the more massive and smaller primaries, respectively.

The distances (r₁) and (r₂) of the third body from the two primaries (m₁) and (m₂), respectively, in the rotating coordinate system are given by

${\text{r}}_1^2={\left(\text{x}-\text{μ}\right)}^2+{\text{y}}^2$ ,  (4)

${\text{r}}_2^2={\left(\text{x}+1-\text{μ}\right)}^2+{\text{y}}^2$ ,  (5)

$\begin{array}{l}\frac{\partial \text{Ω}}{\partial \text{x}}={\text{n}}^2\text{x}-\frac{{\text{q}}_1\left(1-\text{μ}\right)\left(\text{x}-\text{μ}\right)}{{\text{r}}_1{}^3}-\frac{{\text{q}}_2\left(-\text{μ}+\text{x}+1\right)\text{μ}}{{\text{r}}_2{}^3}\\ -\frac{3{\text{A}}_1{\text{q}}_1\left(1-\text{μ}\right)\left(\text{x}-\text{μ}\right)}{2{\text{r}}_1{}^5}-\frac{3{\text{A}}_2{\text{q}}_2\left(-\text{μ}+\text{x}+1\right)\text{μ}}{2{\text{r}}_2{}^5}\end{array}$   (6)

$\frac{\partial \text{Ω}}{\partial \text{y}}=\text{y}\left[{\text{n}}^2-\frac{{\text{q}}_1\left(1-\text{μ}\right)}{{\text{r}}_1{}^3}-\frac{{\text{q}}_2\text{μ}}{{\text{r}}_2{}^3}-\frac{3{\text{A}}_1{\text{q}}_1\left(1-\text{μ}\right)}{2{\text{r}}_1{}^5}-\frac{3{\text{A}}_2{\text{q}}_2\text{μ}}{2{\text{r}}_2{}^5}\right]$ .  (7)

$\frac{\partial \text{Ω}}{\partial \text{x}}\text{and}\frac{\partial \text{Ω}}{\partial \text{y}}$ are partial derivatives of Ω w.r.t. x and y, respectively.

Mean motion

Following Sharma and Subba Rao,⁷ AbdulRaheemand and Singh¹⁴ and Singh and Ishwar² and others had used the mean motion (n) as:

${\text{n}}^2=1+\frac{3}{2}{\text{A}}_1+\frac{3}{2}{\text{A}}_2$ .  (8)

Sharma et al.¹ derived another expression of mean motion by including the secular effects of oblateness on mean anomaly (M), argument of perigee (ω) and right ascension of ascending node (Ω) as (for inclination i = 0 degrees):

$\frac{d{M}_s}{dt}=n\left[1+\frac{3J_2}{2a^2{(1-e^2)}^{\frac{3}{2}}}\right],\frac{d{\omega }_s}{dt}=n\left[\frac{3J_2}{a^2{(1-e^2)}^2}\right],\frac{d{\Omega }_s}{dt}=n\left[\frac{-3J_2}{2a^2{(1-e^2)}^2}\right].$   (9)

Using the relationship,$ndt=(1-e\cos E)dE$  in Eq.(9)and averaging over one revolution:

$\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}d{M}_s=\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}\left[1+\frac{3J_s}{2a^2{(1-e^2)}^{\frac{3}{2}}}\right](1-e\cos E)dE$   (10)

$\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}d{\omega }_s=\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}\left[\frac{3J_s}{a^2{(1-e^2)}^2}\right](1-e\cos E)dE$   (11)

$\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}d{\Omega }_s=\frac{1}{2\pi }\underset{0}{\overset{2\pi }{\int }}\left[\frac{-3J_s}{2a^2{(1-e^2)}^2}\right](1-e\cos E)dE$   (12)

we obtain

$\overline{n}-1+\frac{3J_s}{2a^2{(1-e^2)}^{\frac{3}{2}}}, \Delta {\omega }_s=\frac{3J_s}{a^2{(1-e^2)}^2}, \Delta {\Omega }_s=\frac{3J_s}{2a^2{(1-e^2)}^2}$   (13)

Pseudo mean motion including the precession effect due to oblateness in view of Eq. (13) is calculated as:

$\tilde{n}=\overline{n}+ \Delta {\omega }_s+\Delta {\Omega }_s=1+\frac{3A_1{R}^2}{2a^2{[(1-e^2)R_e]}^2}(1+\sqrt{1-e^2}),A_1=\frac{J_2{R}_e^2}{R^2},$   (14)

which gives ñ = 1 for unperturbed case.

When the value of eccentricity e becomes zero, we get n = ñ = 1 + 3A₁R²/(a²R_e²), which upon non-dimensionalizing gives.^1,5

n = 1 + 3 A₁.  (15)

n² = 1 + 6 A₁, restricting to only first-order terms in A₁.  (16)

In our problem both the primaries are considered as oblate spheroids. So, we consider the mean motion as:

${\text{n}}^2=1+6{\text{A}}_1+6{\text{A}}_2.$   (17)

This mean motion is also used by Jency et al.,⁵ Arohan and Sharma,⁴ John and Sharma¹⁹ and Kumar et al.²⁰

Location of triangular equilibrium points

The location of the triangular points is found from the following two equations for y≠0:

${\text{Ω}}_{\text{x}}={\text{Ω}}_{\text{y}}=0.$   (18)

Equation (18) can be written in terms of equation (19) and (20) as:

${\text{n}}^2\text{x}-\frac{{\text{q}}_1\left(1-\text{μ}\right)\left(\text{x}-\text{μ}\right)}{{\text{r}}_1{}^3}-\frac{{\text{q}}_2\left(-\text{μ}+\text{x}+1\right)\text{μ}}{{\text{r}}_2{}^3}-\frac{3{\text{A}}_1{\text{q}}_1\left(1-\text{μ}\right)\left(\text{x}-\text{μ}\right)}{2{\text{r}}_1{}^5}-\frac{3{\text{A}}_2{\text{q}}_2\left(-\text{μ}+\text{x}+1\right)\text{μ}}{2{\text{r}}_2{}^5}=0$   (19)

$\text{y}\left[{\text{n}}^2-\frac{{\text{q}}_1\left(1-\text{μ}\right)}{{\text{r}}_1{}^3}-\frac{{\text{q}}_2\text{μ}}{{\text{r}}_2{}^3}-\frac{3{\text{A}}_1{\text{q}}_1\left(1-\text{μ}\right)}{2{\text{r}}_1{}^5}-\frac{3{\text{A}}_2{\text{q}}_2\text{μ}}{2{\text{r}}_2{}^5}\right]=0$   (20)

We note for y≠0 in equation (20) and only second term is zero.

Following Singh and Ishwar,² (19) and (20) can be written as

$-\frac{{\text{q}}_1}{{\text{r}}_1{}^3}-\frac{3{\text{A}}_1{\text{q}}_1}{2{\text{r}}_1{}^5}+{\text{n}}^2=0$   (21)

$-\frac{{\text{q}}_2}{{\text{r}}_2{}^3}-\frac{3{\text{A}}_2{\text{q}}_2}{2{\text{r}}_2{}^5}+{\text{n}}^2=0$   (22)

Substituting

${\text{q}}_1=1-{\text{ε}}_1,$   (23)

${\text{q}}_2=1-{\text{ε}}_2,$   (24)

and

$r_2=1+\beta .$   (25)

${\text{r}}_2=1+\text{β}.$   (26)

Substituting(25) and (26) in (4) and (5) and noting that perturbation terms α and β << 1so that the higher order terms of α and β are neglected, we solve for x and y in terms of α and β and obtain:

$\text{x}=-\frac{1}{2}\left[1-2\text{μ}+2\left(\text{α}-\text{β}\right)\right],$   (27)

$\text{y}=\pm \frac{\sqrt{3}}{2}\left[1+\frac{2}{3}\left(\text{α}+\text{β}\right)\right].$   (28)

Substituting (17), (23), (24), (25) and (26) in (21) and (22) and solving for α and β with MAXIMA²¹ software, we obtain

$\text{α}=-\frac{2{\text{ε}}_1+12{\text{A}}_2+9{\text{A}}_1}{6},$   (29)

$\text{β}=-\frac{2{\text{ε}}_2+9{\text{A}}_2+12{\text{A}}_1}{6}$ .  (30)

Substituting (29) and (30) in (27) and (28) and simplifying, we get

$\text{x}=\left[\frac{6\text{μ}-2{\text{ε}}_2+2{\text{ε}}_1+3{\text{A}}_2-3{\text{A}}_1-3}{6}\right]$   (31)

$\text{y}=\pm \sqrt{3}\left[\frac{-2{\text{ε}}_2-2{\text{ε}}_1-21{\text{A}}_2-21{\text{A}}_1+9}{18}\right]$   (32)

The values of A₁ and A₂ are different in y in (32) from those of Singh and Ishwar² due to different value of mean motion n.

For the unperturbed case, (31) and (32) become

$\text{x}=\text{μ}-\frac{1}{2},$   (33)

$\text{y}=\pm \frac{\sqrt{3}}{2},$   (34)

which matches with the case of unperturbed restricted three-body problem.

Stability of the triangular points

At the triangular point L₄:

${\text{Ω}}_{\text{xx}}=\frac{1}{4}\left[\left(-6{\text{ε}}_2+6{\text{ε}}_1+12{\text{A}}_2-12{\text{A}}_1\right)\text{μ}+4{\text{ε}}_2-2{\text{ε}}_1+24{\text{A}}_2+36{\text{A}}_1+3\right],$   (35)

${\text{Ω}}_{\text{yy}}=\frac{1}{4}\left[\left(6{\text{ε}}_2-6{\text{ε}}_1\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1+48{\text{A}}_2+48{\text{A}}_1+9\right],$   (36)

${\text{Ω}}_{\text{xy}}=\frac{\sqrt{3}}{12}\left[\left(2{\text{ε}}_2+2{\text{ε}}_1+138{\text{A}}_2+138{\text{A}}_1+18\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1-60{\text{A}}_2-78{\text{A}}_1-9\right].$   (37)

The characteristic equation is

${\text{λ}}^4+\left(4{\text{n}}^2-{\text{Ω}}_{\text{xx}}-{\text{Ω}}_{\text{yy}}\right){\text{λ}}^2+{\text{Ω}}_{\text{xx}}{\text{Ω}}_{\text{yy}}-{\text{Ω}}_{\text{xy}}{}^2=0$   (38)

Substituting (35), (36), (37) in (38) and simplifying with the help of MAXIMA, we get

$\begin{array}{l}{\text{λ}}^4+{\text{λ}}^2\left(\begin{array}{l}\frac{\left(6{\text{ε}}_2-6{\text{ε}}_1-12{\text{A}}_2+12{\text{A}}_1\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1-24{\text{A}}_2-36{\text{A}}_1-3}{4}\\ +\frac{-\left(6{\text{ε}}_2-6{\text{ε}}_1\right)\text{μ}+4{\text{ε}}_2-2{\text{ε}}_1-48{\text{A}}_2-48{\text{A}}_1-9}{4}+4\left(6{\text{A}}_2+6{\text{A}}_1+1\right)\end{array}\right)+\\ \frac{\begin{array}{l}\left(\left(-6{\text{ε}}_2+6{\text{ε}}_1+12{\text{A}}_2-12{\text{A}}_1\right)\text{μ}+4{\text{ε}}_2-2{\text{ε}}_1+24{\text{A}}_2+36{\text{A}}_1+3\right)\\ \left(\left(6{\text{ε}}_2-6{\text{ε}}_1\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1+48{\text{A}}_2+48{\text{A}}_1+9\right)\end{array}}{16}-\\ \frac{{\left(\left(2{\text{ε}}_2+2{\text{ε}}_1+138{\text{A}}_2+138{\text{A}}_1+18\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1-60{\text{A}}_2-78{\text{A}}_1-9\right)}^2}{48}=0\end{array}$   (39)

Substituting Λ = λ²_, in equation (39), we get this

$\begin{array}{l}{\text{Λ}}^2+\text{Λ }\{\frac{1}{4}[\left(6{\text{ε}}_2-6{\text{ε}}_1-12{\text{A}}_2+12{\text{A}}_1\right)\text{μ}\\ -4{\text{ε}}_2+2{\text{ε}}_1-24{\text{A}}_2-36{\text{A}}_1-3\left]+\frac{1}{4}\right[\left(6{\text{ε}}_1-6{\text{ε}}_2\right)\text{μ}+4{\text{ε}}_2-2{\text{ε}}_1-\\ 48{\text{A}}_2-48{\text{A}}_1-9+4\left(6{\text{A}}_2+6{\text{A}}_1+1\right)]\}\\ +\frac{1}{16}\{\left[\left(-6{\text{ε}}_2+6{\text{ε}}_1+12{\text{A}}_2-12{\text{A}}_1\right)\text{μ}+4{\text{ε}}_2-2{\text{ε}}_1+24{\text{A}}_2+36{\text{A}}_1+3\right]\\ \times \left[\left(6{\text{ε}}_2-6{\text{ε}}_1\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1+48{\text{A}}_2+48{\text{A}}_1+9\right]\}\\ -\frac{1}{48}{\left[\left(2{\text{ε}}_2+2{\text{ε}}_1+138{\text{A}}_2+138{\text{A}}_1+18\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1-60{\text{A}}_2-78{\text{A}}_1-9\right]}^2=\\ 0.\end{array}$   (40)

Solving the quadratic equation (40), we get the roots in the form:

${\Lambda }_1=\frac{\sqrt{(6{\epsilon }_2+6{\epsilon }_1+414A_2+414A_1+27){\mu }^2+(-6{\epsilon }_2-6{\epsilon }_1-420A_2-408A_1-27)\mu +12A_2+6A_1+1}+(3A_2-3A_1)\mu -6A_2-3A_1-1}{2}$   (41)

${\Lambda }_2=\frac{-\sqrt{(6{\epsilon }_2+6{\epsilon }_1+414A_2+414A_1+27){\mu }^2+(-6{\epsilon }_2-6{\epsilon }_1-420A_2-408A_1-27)\mu +12A_2+6A_1+1}+(3A_1-3A_2)\mu -6A_2-3A_1-1}{2}$   (42)

Simplifying (41) and (42) in series form with MAXIMA²¹ and retaining the linear terms in A₁, A₂, ${\epsilon }_1$ and, ${\epsilon }_2$ we get

${\text{Λ}}_1=\frac{\begin{array}{l}\left(6{\text{ε}}_2+6{\text{ε}}_1+414{\text{A}}_2+414{\text{A}}_1+27\right){\text{μ}}^2\\ +\left(-6{\text{ε}}_2-6{\text{ε}}_1-414{\text{A}}_2-414{\text{A}}_1-27\right)\text{μ}\end{array}}{4},$   (43)

${\text{Λ}}_2=-\frac{\begin{array}{l}\left(6{\text{ε}}_2+6{\text{ε}}_1+414{\text{A}}_2+414{\text{A}}_1+27\right){\text{μ}}^2\\ +\left(-6{\text{ε}}_2-6{\text{ε}}_1-426{\text{A}}_2-402{\text{A}}_1-27\right)\text{μ}\\ +24{\text{A}}_2+12{\text{A}}_1+4\end{array}}{4}$   (44)

Critical mass ratio

Taking the discriminant D in (40) and after simplification, we get

$\begin{array}{l}\text{D}=\left(6{\text{ε}}_2+6{\text{ε}}_1+414{\text{A}}_2+414{\text{A}}_1+27\right){\text{μ}}^2\\ +\left(-6{\text{ε}}_2-6{\text{ε}}_1-420{\text{A}}_2-408{\text{A}}_1-27\right)\text{μ}+12{\text{A}}_2+6{\text{A}}_1+1.\end{array}$   (45)

Equating D = 0 and solving Eq. (45), we get two values of the mass ratio: (μ)

${\text{μ}}_1=\frac{\begin{array}{l}\sqrt{3}\sqrt{100{\text{ε}}_2+100{\text{ε}}_1+6576{\text{A}}_2+6576{\text{A}}_1+207}\\ +6{\text{ε}}_2+6{\text{ε}}_1+420{\text{A}}_2+408{\text{A}}_1+27\end{array}}{12{\text{ε}}_2+12{\text{ε}}_1+828{\text{A}}_2+828{\text{A}}_1+54}$   (46)

${\text{μ}}_2=\frac{\begin{array}{l}-\sqrt{3}\sqrt{100{\text{ε}}_2+100{\text{ε}}_1+6576{\text{A}}_2+6576{\text{A}}_1+207}\\ +6{\text{ε}}_2+6{\text{ε}}_1+420{\text{A}}_2+408{\text{A}}_1+27\end{array}}{12{\text{ε}}_2+12{\text{ε}}_1+828{\text{A}}_2+828{\text{A}}_1+54}$   (47)

(μ_c) in the range [0, ½]. The triangular points are linearly stable for the mass parameter 0 ≤ μ <μ_c). After simplifications with MAXIMA²¹ and retaining first-order terms in A₁, A₂, ε₁ and ε₂, we get

${\text{μ}}_{\text{c}}=\frac{1}{2}\left[1-\frac{\sqrt{69}}{9}\right]-\frac{A_1}{9}\left[1+\frac{19}{\sqrt{69}}\right]+\frac{A_2}{9}\left[1-\frac{19}{\sqrt{69}}\right]-\frac{2}{27\sqrt{69}}\left({\epsilon }_1+{\epsilon }_2\right).$   (48)

${\mu }_c=0.0385208965-0.3652590232A_1-0.1430368010A_2-0.0089174706{\epsilon }_1-0.0089174706{\epsilon }_2.$   (49)

The expression for ${\text{μ}}_{\text{c}}$ up to first-order terms in A₁, A₂, ε₁ and ε₂, obtained by Singh and Ishwar² is

${\text{μ}}_{\text{c}}=\frac{1}{2}\left[1-\frac{\sqrt{69}}{9}\right]-2/\left\{9\sqrt{69} \right\}\left(A_1+A_2\right)-\frac{2}{27\sqrt{69}}\left({\epsilon }_1+{\epsilon }_2\right)$ .  (50)

or

${\mu }_c=0.0385208965–0.0267524118\left(A_1+A_2\right)-0.0089174706({\text{ε}}_1+{\text{ ε}}_2).$   (51)

From (49) and (51), we notice that with the new mean motion, the value of the critical mass μ_c further decreases.

It may be noted that the first two terms of critical mass ratio ${\mu }_{\text{c}}$  in equation (49) match with Jency et al.,⁵ who utilize the same expression of mean motion as used here by considering the more massive primary as an oblate spheroid. It may also be pointed out that the critical mass ratio ${\mu }_{\text{c}}$  obtained by Arohan and Sharma⁴ with the same mean motion expression by considering the smaller primary as an oblate spheroid does not match with our result here. They get the term 0.1194 A₂ in the critical mass expression ${\mu }_{\text{c}}$ i.e., it increases with oblateness of the smaller primary. However, our term with ε₁ matched with the ε term of Arohan and Sharma.⁴

We conclude from the present study that the critical mass value ${\mu }_{\text{c}}$ further decreases with oblateness with the new mean motion n when both the primaries are considered as oblate spheroids.

Periodic orbits

Angular frequencies

The angular frequencies can be calculated using the following relations

${\text{λ}}_{1,2}=\pm {\left(-{\text{Λ}}_1\right)}^{\frac{1}{2}}=\pm {\text{is}}_4$  

${\text{λ}}_{3,4}=\pm {\left(-{\text{Λ}}_2\right)}^{\frac{1}{2}}=\pm {\text{is}}_5$  

for long-periodic (S₄) and short-periodic (S₃) orbits around L₄, respectively.

${\text{s}}_4={\left(-{\text{Λ}}_1\right)}^{\frac{1}{2}}$   (52)

${\text{s}}_5={\left(-{\text{Λ}}_2\right)}^{\frac{1}{2}}$   (53)

Substituting (43) and (44) in (52) and (53), respectively, we have

${\text{s}}_4=\frac{\sqrt{\begin{array}{l}-\sqrt{\begin{array}{l}\left(6{\text{ε}}_2+6{\text{ε}}_1+414{\text{A}}_2+414{\text{A}}_1+27\right){\text{μ}}^2\\ +\left(-6{\text{ε}}_2-6{\text{ε}}_1-420{\text{A}}_2-408{\text{A}}_1-27\right)\text{μ}+12{\text{A}}_2+6{\text{A}}_1+1\end{array}}\\ -\left(3{\text{A}}_2-3{\text{A}}_1\right)\text{μ}+6{\text{A}}_2+3{\text{A}}_1+1\end{array}}}{\sqrt{2}}$   (54)

${\text{s}}_5=\frac{\sqrt{\begin{array}{l}\sqrt{\begin{array}{l}\left(6{\text{ε}}_2+6{\text{ε}}_1+414{\text{A}}_2+414{\text{A}}_1+27\right){\text{μ}}^2\\ +\left(-6{\text{ε}}_2-6{\text{ε}}_1-420{\text{A}}_2-408{\text{A}}_1-27\right)\text{μ}+12{\text{A}}_2+6{\text{A}}_1+1\end{array}}\\ +\left(3{\text{A}}_1-3{\text{A}}_2\right)\text{μ}+6{\text{A}}_2+3{\text{A}}_1+1\end{array}}}{\sqrt{2}}$   (55)

Simplifying (54) and (55) with MAXIMA in terms of a series up to third-order terms in μ, we get

${\text{s}}_4=\frac{3^{\frac{3}{2}}\sqrt{\text{μ}}}{2}\left[\begin{array}{l}\left(1+\frac{23\text{μ}}{8}+\frac{4439{\text{μ}}^2}{128}+\frac{548711{\text{μ}}^3}{1024}\right)\\ +{\text{ A}}_1\left(\frac{37}{6}+\frac{2291\text{μ}}{48}+\frac{680627{\text{μ}}^2}{768}+\frac{114994403{\text{μ}}^3}{6144}\right)+\\ {\text{A}}_2\left(\frac{14}{3}+\frac{157\text{μ}}{6}+\frac{83579{\text{μ}}^2}{192}+\frac{3334505{\text{μ}}^3}{384}\right)+\\ {\text{ε}}_1\left(\frac{1}{9}+\frac{77\text{μ}}{72}+\frac{23555{\text{μ}}^2}{1152}+\frac{4040297{\text{μ}}^3}{9216}\right)\\ +{\text{ε}}_2\left(\frac{1}{9}+\frac{77\text{μ}}{72}+\frac{23555{\text{μ}}^2}{1152}+\frac{4040297{\text{μ}}^3}{9216}\right)\end{array}\right]$   (56)

$\begin{array}{l}{\text{s}}_5=1-\frac{27\text{μ}}{8}-\frac{3213{\text{μ}}^2}{128}-\frac{355023{\text{μ}}^3}{1024}\\ +{\text{A}}_1\left(\frac{3}{2}-\frac{561\text{μ}}{16}-\frac{133767{\text{μ}}^2}{256}-\frac{21453741{\text{μ}}^3}{2048}\right)\\ +{\text{A}}_2\left(3-\frac{183\text{μ}}{8}-\frac{34443{\text{μ}}^2}{128}-\frac{5100327{\text{μ}}^3}{1024}\right)+\\ {\text{ε}}_1\left(-\frac{3\text{μ}}{4}-\frac{381{\text{μ}}^2}{32}-\frac{124821{\text{μ}}^3}{512}\right)+{\text{ε}}_2\left(-\frac{3\text{μ}}{4}-\frac{381{\text{μ}}^2}{32}-\frac{124821{\text{μ}}^3}{512}\right).\end{array}$   (57)

It may be noted that s₄ in (56) increases with oblateness (A₁ and A₂) and radiation pressure (ε₁and ε₂). It may also be noted that the unperturbed values in s₄ in (56) match with the unperturbed expression in Sharma and Subba Rao.⁸ The A₁ values in (56) match with the expression obtained by Jency et al.⁵ Similarly, the unperturbed values in s₅ in (57) match with the unperturbed expression in Sharma and Subba Rao. The A₁ values in (57) match with the expression obtained by Jency et al.⁵

Table 1 provides the variation of the angular frequencies (s₄) and (s₅) for mass ratioμ = 0.001 with different perturbations in A₁, A₂, ε₁ and ε₂. It may be noted that s₄ increases with all the 4 perturbations. s₅ decreases with radiation pressure perturbations ε₁ and ε₂. Figure 2 provided the angular frequency of the long- periodic orbits (s₄) vs. Mass ratio μ for different values of perturbations. It is observed that s₄ increases with the increase in μ for different cases of perturbations in A₁, A₂, ε₁ and ε₂.

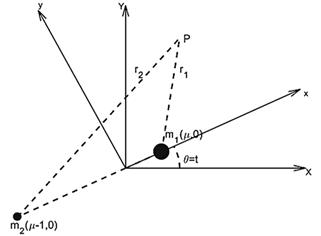
Figure 1 Planar Restricted Three Body Problem in the fixed (sidereal) and rotating (synodic) coordinate system.

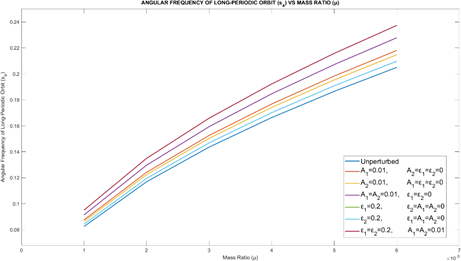
Figure 2 Angular frequency of the long-periodic orbits (s4) vs.mass ratio (μ).

Figure 3 provided the angular frequency of the short- periodic orbits (s₅) vs. Mass ratio μ for different values of perturbations.  It is observed that s₅ decreases with the increase in μ for different cases of perturbations in A₁, A₂, ε₁ and ε₂.

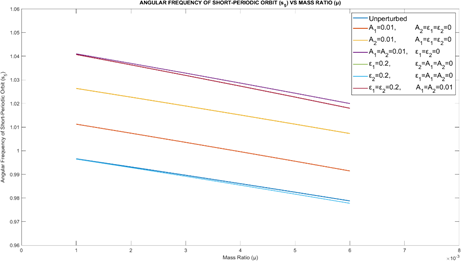
Figure 3Angular frequency of the short-periodic orbits (s5) vs.mass ratio (μ).

Eccentricities

The eccentricities of the long-periodic and short-periodic orbits around L₄ are given by

$\text{e}=\frac{\sqrt{2}{\left({\left({\text{Ω}}_{\text{xx}}-{\text{Ω}}_{\text{yy}}\right)}^2+4{\text{Ω}}_{\text{xy}}^2\right)}^{\frac{1}{4}}}{\sqrt{{\text{Ω}}_{\text{yy}}+\sqrt{{\left({\text{Ω}}_{\text{xx}}-{\text{Ω}}_{\text{yy}}\right)}^2+4{\text{Ω}}_{\text{xy}}^2}+{\text{Ω}}_{\text{xx}}+2\text{s}}}$   (58)

By substituting the corresponding angular frequencies, $(s_4)$ and $(s_5)$ in Eq.(58) and simplifying in series form with MAXIMA,²¹ we get the corresponding eccentricities (e₄) and (e₅) of the long- and short-periodic orbits, respectively.

The eccentricity of long-periodic orbits (e₄) is:

$\begin{array}{l}{\text{e}}_4=-\frac{153713{\text{ε}}_2{\text{μ}}^4}{128}-\frac{153713{\text{ε}}_1{\text{μ}}^4}{128}-\frac{27673863{\text{A}}_2{\text{μ}}^4}{1024}\\ -\frac{110019675{\text{A}}_1{\text{μ}}^4}{2048}-\frac{1316205{\text{μ}}^4}{1024}-\frac{1763{\text{ε}}_2{\text{μ}}^3}{32}-\\ \frac{1763{\text{ε}}_1{\text{μ}}^3}{32}-\frac{86631{\text{A}}_2{\text{μ}}^3}{64}-\frac{324039{\text{A}}_1{\text{μ}}^3}{128}-\frac{4977{\text{μ}}^3}{64}\\ -\frac{35{\text{ε}}_2{\text{μ}}^2}{12}-\frac{35{\text{ε}}_1{\text{μ}}^2}{12}-\frac{1285{\text{A}}_2{\text{μ}}^2}{16}-\\ \frac{4325{\text{A}}_1{\text{μ}}^2}{32}-\frac{93{\text{μ}}^2}{16}-\frac{{\text{ε}}_2\text{μ}}{3}-\frac{{\text{ε}}_1\text{μ}}{3}-\frac{19{\text{A}}_2\text{μ}}{2}-\frac{47{\text{A}}_1\text{μ}}{4}-\frac{3\text{μ}}{2}+1.\end{array}$   (59)

The eccentricity of short-periodic orbits (e₅) is:

${\text{e}}_5=\frac{\sqrt{3}}{2}\left(\begin{array}{l}\frac{4258317{\text{ε}}_2{\text{μ}}^4}{4096}+\frac{4258317{\text{ε}}_1{\text{μ}}^4}{4096}+\frac{383440059{\text{A}}_2{\text{μ}}^4}{16384}\\ +\frac{3048483753{\text{A}}_1{\text{μ}}^4}{65536}+\frac{36506349{\text{μ}}^4}{32768}+\frac{24153{\text{ε}}_2{\text{μ}}^3}{512}\\ +\frac{24153{\text{ε}}_1{\text{μ}}^3}{512}+\frac{298629{\text{A}}_2{\text{μ}}^3}{256}+\frac{4473063{\text{A}}_1{\text{μ}}^3}{2048}\\ +\frac{69147{\text{μ}}^3}{1024}+\frac{199{\text{ε}}_2{\text{μ}}^2}{96}+\frac{199{\text{ε}}_1{\text{μ}}^2}{96}\\ +\frac{3997{\text{A}}_2{\text{μ}}^2}{64}+\frac{28057{\text{A}}_1{\text{μ}}^2}{256}+\frac{573{\text{μ}}^2}{128}+\frac{{\text{ε}}_2\text{μ}}{12}+\frac{{\text{ε}}_1\text{μ}}{12}\\ +\frac{17{\text{A}}_2\text{μ}}{2}+\frac{183{\text{A}}_1\text{μ}}{16}+\frac{3\text{μ}}{8}+\frac{{\text{A}}_1}{2}+1\end{array}\right).$   (60)

The series expansion expressions for e₄ and e₅ in (59) and (60) are new results. It is noticed that e₄ decreases with the increase in the perturbations A₁, A₂, ε₁ and ε₂. And e₅ increases with the increase in the perturbations A₁, A₂, ε₁ and ε₂.

Table 2 provides the variation of the eccentricities (e₄) and (e₅) for mass ratio μ = 0.001 with different perturbations in A₁, A₂, ε₁ and ε₂. It may be noted that e₄ decreases with all the 4 perturbations. e₅ increases with all the 4 perturbations.

Figure 4 provides the eccentricity of the long- periodic orbits (e₄) vs. Mass ratio μ for different values of perturbations. It is observed that e₄decreases with the increase in the mass ratio (μ) for different cases of perturbations in A₁, A₂, ε₁ and ε₂.

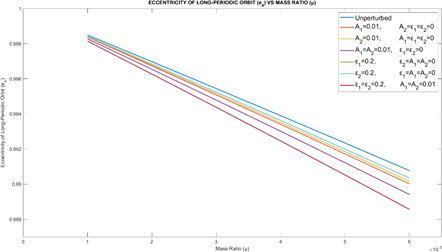
Figure 4 Eccentricity of the long-periodic orbits (e4) vs.Mass ratio (μ).

Figure 5 provides the eccentricity of the short- periodic orbits (e₅) vs. Mass ratio μ for different values of perturbations.  It is observed that e₅increases with the increase in the mass ratio (μ) for different cases of perturbations in A₁, A₂, ε₁ and ε₂.

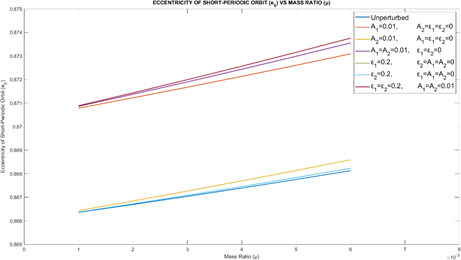
Figure 5 Eccentricity of the short-periodic orbits (e5) vs.Mass ratio (μ).

Time periods

Time periods of the long-periodic (T₄) and short-periodic (T₅) orbits around L₄ are given respectively

${\text{T}}_4=\frac{2\text{π}}{{\text{s}}_4}$   (61)

${\text{T}}_5=\frac{2\text{π}}{{\text{s}}_5}$   (62)

Table 3 provides the variation of the time periods (T₄) and (T₅) for mass ratio μ = 0.001 with different perturbations in A₁, A₂, ε₁ and ε₂. It may be noted that T₄ decreases with all the 4 perturbations, while T₅ decreases with oblateness of the primaries and increases with radiation pressure perturbations ε₁ and ε₂. As seen in the last line over all it decreases significantly, showing the dominance of oblateness.

Angle α:

(Figure 6) where α is the angle between the rotating and the fixed coordinate system.

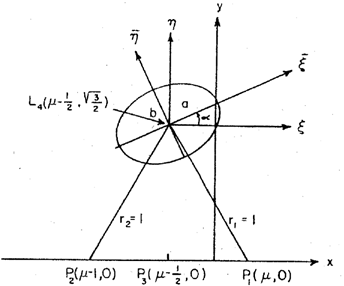
Figure 6 Fixed and Rotating coordinate system at L₄.⁶

The angle α given by

$\text{tan}2\text{α}=\frac{2{\text{Ω}}_{\text{xy}}}{{\text{Ω}}_{\text{xx}}-{\text{Ω}}_{\text{yy}}}$   (63)

Substituting (35), (36) and (37) in (63) and simplifying with MAXIMA, we get

$\text{tan}2\text{α}=\frac{\begin{array}{l}\left(2{\text{ε}}_2+2{\text{ε}}_1+138{\text{A}}_2+138{\text{A}}_1+18\right)\text{μ}\\ -4{\text{ε}}_2+2{\text{ε}}_1-60{\text{A}}_2-78{\text{A}}_1-9\end{array}}{6\left(\begin{array}{l}\frac{\left(-6{\text{ε}}_2+6{\text{ε}}_1+12{\text{A}}_2-12{\text{A}}_1\right)\text{μ}+4{\text{ε}}_2-2{\text{ε}}_1+24{\text{A}}_2+36{\text{A}}_1+3}{4}\\ -\frac{\left(6{\text{ε}}_2-6{\text{ε}}_1\right)\text{μ}-4{\text{ε}}_2+2{\text{ε}}_1+48{\text{A}}_2+48{\text{A}}_1+9}{4}\end{array}\right)}$  (64)

Simplifying (64) with MAXIMA, we get

$\tan 2\alpha =\sqrt{3}\left(-2\mu +\frac{8A_2(1-2\mu )}{3}+\frac{20A_1(1-2\mu )}{3}-\frac{4{\epsilon }_1(2-7\mu )}{9}+\frac{4{\epsilon }_2(4-11\mu )}{9}+1\right).$   (65)

Eq. (65) shows that α increases with oblateness and decreases with radiation force of the more massive primary and increases with the radiation force of the smaller primary.  It is noticed that our expression of tan2α matches with that of Jency et al.⁵ for A₁ term. Our results of tan2α do not match with ε₁ and ε₂ terms with that of Abouelmagd and El-Shaboury.³

Location of the triangular Lagrangian points is found with the new mean motion of Sharma et al.¹ The critical mass ratio μ_c is obtained. This value of critical mass ratio μ_c matches with that of Jency et al.⁵ for A₁ term. This value also decreases with oblateness and radiation pressure of both the primaries. The angular frequencies (s₄) of the long- and (s₅) short-periodic orbits around L₄ are obtained in the series form up to linear terms in oblateness and radiation pressure of both the primaries. These expressions match with Jency et al.⁵ with A₁ terms. It may be noted that s₄ increases with all the 4 perturbations and s₅ decreases with radiation pressure perturbations ε₁ and ε₂. The series expansion expressions for e₄ and e₅ are derived. It may be noted that e₄ decreases with all the 4 perturbations and e₅ increases with all the 4 perturbations. It may be pointed out that the series expansion expressions for e₄ and e₅ are new results. We also found the time-periods of long-(T₄) and short-periodic orbits (T₅) around L₄. It is that T₄ decreases with all the 4 perturbations, while T₅ decreases with oblateness of the primaries and increases with radiation pressure perturbations ε₁ and ε₂. The angle α between the rotating and the fixed coordinate system is also computed in series form. Our expression of tan2α matches with that of Jency et al.⁵ for A₁ term and does not match with ε₁ and ε₂ terms with that of Abouelmagd and El-Shaboury.³ 

Location of the triangular Lagrangian point (L₄) is obtained with the new motion expression of Sharma et al.¹ Linear stability of the triangular Lagrangian point is analyzed. In order to study the linear stability, the value of critical mass ratio (μ_c) is calculated. The angular frequencies of the long- and short-periodic orbits around L₄ are computed in series form using MAXIMA software.²¹ The eccentricities of the long and short-periodic orbits around L₄ are also calculated in the series form. The time-periods of the long- and short-periodic orbits around L₄ are calculated and studied their variation with respect to the mass ratio (μ), oblateness and radiation pressure of both the primaries. The angle between the fixed and rotating coordinate system is also computed in the series form. Some of these results are new and are checked with the numerically integrated values.

None.

None.

1. Sharma RK, Sellamuthu H, Jency AA. Perturbed Trojan Dynamics in the Solar System. – In: AAS AIAA Astrodynamics Specialist Conference. 2019;20–704:3599–3618.
2. Singh J, Ishwar B. Stability of the triangular points in the generalized photogravitational restricted three body problem. Bull Astr Soc India. 2019;27:415–424.
3. Abouelmagd EI, El–Shaboury SM. Periodic orbits under combined effects of oblateness and radiation in the restricted problem of three bodies. Astrophys. Space Sci. 2012;341:331–341.
4. Arohan R, Sharma RK. Periodic orbits in the planar restricted photo–gravitational problem when the smaller primary is an oblate spheroid. Indian Journal of Science and Technology. 2020;13(16):1630–1640.
5. Jency AA, Sharma RK, Singh G. Stationary solutions, critical mass, Tadpole orbits in the circular restricted three–body problem with the more massive primary as an oblate spheroid. Indian Journal of Science and Technology. 2019;13(39):4168–4188.
6. Szebehely V.  Theory of Orbits. Academic Press. New York; 1967.
7. Sharma R, Subba Rao PV. Stationary Solutions and Their Characteristic Exponents in the Restricted Three–Body Problem When the More Massive Primary Is an Oblate Spheroid. Celestial mechanics. 1976;13:137–149.
8. Sharma RK, Subba Rao PV. A case of commensurability induced by oblateness. Celestial Mechanics. 1978;18:185–194.
9. Sharma RK, Subba Rao PV. Effect of oblateness on triangular solutions at critical mass. Astrophysics and Space Science. 1979;60:247–250.
10. Subba Rao PV, Sharma RK. A note on the stability of the triangular points of equilibrium in the restricted three–body problem. Astronomy and Astrophysics. 1975;43:381–383.
11. Sharma RK. On linear stability of triangular libration points of the photogravitational three–body problem when the more massive primary is an oblate spheroid. In: Fricke W, Teleki G, editors. Sun and Planetary System, D. Reidel Publishing Co. Dordrecht, Holland.1982;435–436.
12. Sharma RK. The Linear Stability of Liberation Points of The Photogravitational Restricted Three–Body Problem When the Smaller Primary is an Oblate Spheroid. Astrophys Space Sci. 1987;135:271–281.
13. Subba Rao PV, Sharma RK. Effect of oblateness on the non–linear stability of L4 in the restricted three–body problem. Celestial Mechanics and Dynamical Astronomy. 1997;65:291–312.
14. AbdulRaheem A, Singh J. Combined effects of perturbations, radiation, and oblateness on the stability of equilibrium points in the restricted three–body problem. The Astronomical Journal. 2006;131:1880–1885.
15. AbdulRaheem A, Singh J. Combined effects of perturbations, radiation and oblateness on the periodic orbits in the restricted three body problem. Astrophys Space Sci. 2008;317:9–13.
16. Abouelmagd EI. Stability of the Triangular Points under Combined Effects of Radiation and Oblateness in the Restricted Three–Body Problem. Earth Moon Planets. 2013;110:143–155.
17. Ansari AA, Alam M. Dynamics in the circular restricted three body problem with perturbations. International Journal of Advanced Astronomy. 2017;5(1):19–25.
18. Khalifa NS. Location of triangular equilibrium points in the perturbed CR3BP with laser radiation pressure and oblateness. International Journal of Advanced Astronomy. 2018;6(1):8–11.
19. John D, Sharma RK. Periodic orbit in the photo–gravitational restricted three body problem around the collinear Lagrangian points when more massive primary is an oblate spheroid and source of radiation. International Journal of Advanced Astronomy. 2021;9(1):32–37.
20. Kumar D, Sharma RK, Aggarwal R, et al. A note on modified restricted three–body problem. Astronomy Reports. 2022;66(8) ;710–724.
21. MAXIMA: A Computer Algebra System, 1998.