Structural model of a piezo engine for composite telescope

doi:10.15406/paij.2022.06.00243

eISSN: 2576-4543

Physics & Astronomy International Journal

Review Article Volume 6 Issue 1

Structural model of a piezo engine for composite telescope

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, Russia

Correspondence: Afonin Sergey Mikhailovich, National Research University of Electronic Technology, MIET, 124498, Moscow, Russia

Received: February 01, 2022 | Published: February 22, 2022

Citation: Afonin SM. Structural model of a piezo engine for composite telescope. Phys Astron Int J. 2022;6(1):12-15. DOI: 10.15406/paij.2022.06.00243

Download PDF

Abstract

The structural model of a piezo engine for composite telescope is constructed. This structural model clearly shows the conversion of electrical energy by a piezo engine into mechanical energy of the control element of a composite telescope. The structural scheme of a piezo engine is determined. For the control systems with a piezo engine its deformations are obtained in the matrix form. This structural model, structural scheme and matrix equation of a piezo engine are applied in calculation the parameters of the control systems for composite telescope.

Keywords: Piezo engine, Structural model, Structural scheme, Matrix equation, Deformation, Composite telescope

Introduction

A piezo engine based on the piezoelectric effect is used in the control systems for composite telescope and adaptive optics.^1‒14 A piezo engine is applied for precise adjustment, compensation the deformations of composite telescope and scanning microscope.^15‒21 For decisions the displacements and the forces of a piezo engine in the control systems for composite telescope is used the structural model of a piezo engine. The structural model clearly shows the conversion of electrical energy by a piezo engine into mechanical energy of the control element of a composite telescope with using the physical parameters of a engine and its load.^16‒28 The structural model and the structural scheme of a piezo engine for composite telescope are determined in difference from Cady’s and Mason’s electrical equivalent circuits of a piezo transducer.^7‒28

Structural scheme of a piezo engine

The matrix state equations [8, 11‒17] of a piezo engine have the form

$(D) = (d) (T) + (ε^{T}) (E)$ $(D) = (d) (T) + (ε^{T}) (E)$

$(S) = (s^{E}) (T) + {(d)}^{t} (E)$ $(S) = (s^{E}) (T) + {(d)}^{t} (E)$

where $(D)$ $(D)$ , $(S)$ $(S)$ , $(T)$ $(T)$ , $(E)$ $(E)$ are the matrices of electric induction, relative deformation, mechanical field and electric field stresses, and t is transpose operator. For PZT engine the matrices have the form

$(d) = ⎛ ⎜ ⎝ \begin{matrix} \begin{matrix} 0 & 0 & 0 & 0 & d_{15} & 0 \end{matrix} \begin{matrix} 0 & 0 & 0 & d_{15} & 0 & 0 \end{matrix} \begin{matrix} d_{31} & d_{31} & d_{33} & 0 & 0 & 0 \end{matrix} \end{matrix} ⎞ ⎟ ⎠$ $(d) = (\begin{matrix} \begin{matrix} 0_{} & 0_{} & 0_{} & 0_{} & d_{15} & 0 \end{matrix} \\ \begin{matrix} 0_{} & 0_{} & 0_{} & d_{15} & 0_{} & 0 \end{matrix} \\ \begin{matrix} d_{31} & d_{31} & d_{33} & 0_{} & 0_{} & 0_{} \end{matrix} \end{matrix})$

${(d)}^{t} = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ \begin{matrix} 0 & 0 & d_{31} 0 & 0 & d_{31} 0 & 0 & d_{33} 0 & d_{15} & 0 d_{15} & 0 & 0 0 & 0 & 0 \end{matrix} ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠$ ${(d)}^{t} = (\begin{matrix} 0 & 0 & d_{31} \\ 0 & 0 & d_{31} \\ 0 & 0 & d_{33} \\ 0 & d_{15} & 0 \\ d_{15} & 0 & 0 \\ 0 & 0 & 0 \end{matrix})$

$(ε^{T}) = ⎛ ⎜ ⎜ ⎝ \begin{matrix} ε_{11}^{T} & 0 & 0 0 & ε_{22}^{T} & 0 0 & 0 & ε_{33}^{T} \end{matrix} ⎞ ⎟ ⎟ ⎠$ $(ε^{T}) = (\begin{matrix} ε_{11}^{T} & 0 & 0 \\ 0 & ε_{22}^{T} & 0 \\ 0 & 0 & ε_{33}^{T} \end{matrix})$

$(s^{E}) = ⎛ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ \begin{matrix} s_{11}^{E} & s_{12}^{E} & s_{13}^{E} & 0 & 0 & 0 s_{12}^{E} & s_{11}^{E} & s_{13}^{E} & 0 & 0 & 0 s_{13}^{E} & s_{13}^{E} & s_{33}^{E} & 0 & 0 & 0 0 & 0 & 0 & s_{55}^{E} & 0 & 0 0 & 0 & 0 & 0 & s_{55}^{E} & 0 0 & 0 & 0 & 0 & 0 & 2 (s_{11}^{E} - s_{12}^{E}) \end{matrix} ⎞ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠$ $(s^{E}) = (\begin{matrix} s_{11}^{E} & s_{12}^{E} & s_{13}^{E} & 0 & 0 & 0 \\ s_{12}^{E} & s_{11}^{E} & s_{13}^{E} & 0 & 0 & 0 \\ s_{13}^{E} & s_{13}^{E} & s_{33}^{E} & 0 & 0 & 0 \\ 0 & 0 & 0 & s_{55}^{E} & 0 & 0 \\ 0 & 0 & 0 & 0 & s_{55}^{E} & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 (s_{11}^{E} - s_{12}^{E}) \end{matrix})$

The equation of the reverse piezo effect [8‒51] has the form

$S_{i} = d_{m i} E_{m} + s_{i j}^{E} T_{j}$ $S_{i} = d_{m i} E_{m} + s_{i j}^{E} T_{j}$

where m, i, j are axises.

For the longitudinal piezo engine on Figure 1 its parameters are determined in the form

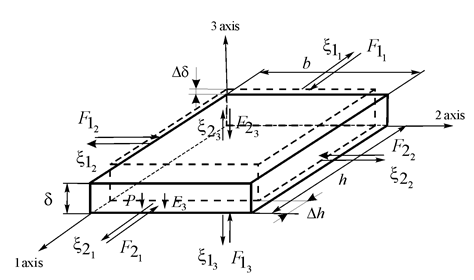
Figure 1 A piezo engine for composite telescope.

$Δ δ_{max} = d_{33} E_{3} δ = d_{33} U$ $Δ δ_{max} = d_{33} E_{3} δ = d_{33} U$ , $F_{max} = d_{33} E_{3} S_{0} / s_{33}^{E}$ $F_{max} = d_{33} E_{3} S_{0} / s_{33}^{E}$

At $d_{33}$ $d_{33}$ = 4∙10^‒10 m/V, $E_{3}$ $E_{3}$ = 0.8∙10⁵ V/m, $δ$ $δ$ = 2.5∙10^‒3 m, $S_{0}$ $S_{0}$ = 1.5∙10^‒4 m², $s_{33}^{E}$ $s_{33}^{E}$ = 15∙10^‒12 m²/N its maximum values of deformation and force are received in the form $Δ δ_{max}$ $Δ δ_{max}$ = 80 nm, $F_{max}$ $F_{max}$ = 320 N with error 10%.

The differential equation for a piezo engine has the form^11‒51

$\frac{d^{2} Ξ (x, s)}{d x^{2}} - γ^{2} Ξ (x, s) = 0$ $\frac{d^{2} Ξ (x, s)}{d x^{2}} - γ^{2} Ξ (x, s) = 0$

where $x$ $x$ , $s$ $s$ , $γ$ $γ$ are coordinate, operator and coefficient.

Its solution has form

$Ξ (x, s) = {Ξ_{1} (s) sh [(l - x) γ] + Ξ_{2} (s) sh (x γ)} / sh (l γ)$ $Ξ (x, s) = {Ξ_{1} (s) sh [(l - x) γ] + Ξ_{2} (s) sh (x γ)} / sh (l γ)$

For the stresses acting on two faces a piezo engine its transforms of Laplace have the form

$T_{j} (0, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} ∣ ∣}_{x = 0} - \frac{d_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)$ $T_{j} (0, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} |}_{x = 0} - \frac{d_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)$

$T_{j} (l, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} ∣ ∣}_{x = l} - \frac{d_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)$ $T_{j} (l, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} |}_{x = l} - \frac{d_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)$

where $Ψ = E$ $Ψ = E$ or $Ψ = D$ $Ψ = D$ .

For the structural model and scheme of a piezo engine for composite telescope on Figure 2 its equations have the form

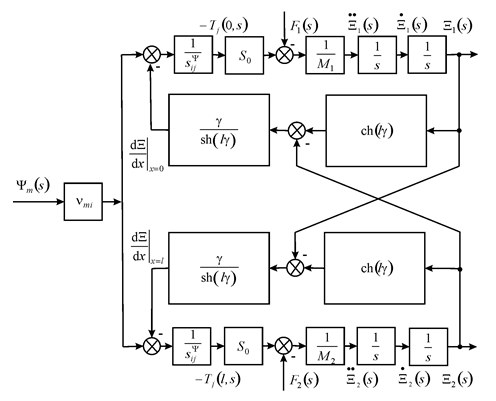
Figure 2 Structural scheme of a piezo engine for composite telescope.

$Ξ_{1} (s) = [1 / (M_{1} s^{2})] {- F_{1} (s) + (1 / χ_{i j}^{Ψ}) [\begin{matrix} d_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \times [ch (l γ) Ξ_{1} (s) - Ξ_{2} (s)] \end{matrix}]}$ $Ξ_{1} (s) = [1 / (M_{1} s^{2})] {- F_{1} (s) + (1 / χ_{i j}^{Ψ}) [\begin{array}{l} d_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{1} (s) - Ξ_{2} (s)] \end{array}]}$

$Ξ_{2} (s) = [1 / (M_{2} s^{2})] {- F_{2} (s) + (1 / χ_{i j}^{Ψ}) [\begin{matrix} d_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \times [ch (l γ) Ξ_{2} (s) - Ξ_{1} (s)] \end{matrix}]}$ $Ξ_{2} (s) = [1 / (M_{2} s^{2})] {- F_{2} (s) + (1 / χ_{i j}^{Ψ}) [\begin{array}{l} d_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{2} (s) - Ξ_{1} (s)] \end{array}]}$

where $v_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} g_{33}, g_{31}, g_{15} \end{matrix}$ $v_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} \\ g_{33}, g_{31}, g_{15} \end{matrix}$ , $Ψ_{m} = {\begin{matrix} E_{3}, E_{1} D_{3}, D_{1} \end{matrix}$ $Ψ_{m} = {\begin{matrix} E_{3}, E_{1} \\ D_{3}, D_{1} \end{matrix}$ , $s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} s_{33}^{D}, s_{11}^{D}, s_{55}^{D} \end{matrix}$ $s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} \\ s_{33}^{D}, s_{11}^{D}, s_{55}^{D} \end{matrix}$ , $l = {δ, h, b$ $l = {δ, h, b$ , $γ = {γ^{E}, γ^{D}$ $γ = {γ^{E}, γ^{D}$ , $c^{Ψ} = {c^{E}, c^{D}$ $c^{Ψ} = {c^{E}, c^{D}$ , $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0}$ , $v_{m i}$ $v_{m i}$ is the piezo coefficient.

Therefore, the matrix equation of a piezo engine has the form

$(\begin{matrix} Ξ_{1} (s) Ξ_{2} (s) \end{matrix}) = (\begin{matrix} \begin{matrix} W_{11} (s) & W_{12} (s) & W_{13} (s) \end{matrix} \begin{matrix} W_{21} (s) & W_{22} (s) & W_{23} (s) \end{matrix} \end{matrix}) ⎛ ⎜ ⎝ \begin{matrix} Ψ_{m} (s) F_{1} (s) F_{2} (s) \end{matrix} ⎞ ⎟ ⎠$ $(\begin{matrix} Ξ_{1} (s) \\ Ξ_{2} (s) \end{matrix}) = (\begin{matrix} \begin{matrix} W_{11} (s) & W_{12} (s) & W_{13} (s) \end{matrix} \\ \begin{matrix} W_{21} (s) & W_{22} (s) & W_{23} (s) \end{matrix} \end{matrix}) (\begin{matrix} Ψ_{m} (s) \\ F_{1} (s) \\ F_{2} (s) \end{matrix})$

The steady‒state displacements of faces 1 and 2 for the longitudinal piezo engine have the form

$ξ_{1} (\infty) = d_{33} U M_{2} / (M_{1} + M_{2})$ $ξ_{1} (\infty) = d_{33} U M_{2} / (M_{1} + M_{2})$

$ξ_{2} (\infty) = d_{33} U M_{1} / (M_{1} + M_{2})$ $ξ_{2} (\infty) = d_{33} U M_{1} / (M_{1} + M_{2})$

At $d_{33}$ $d_{33}$ = 4×10^‒10 m/V, U= 250 V, $M_{1}$ $M_{1}$ = 1 kg and $M_{2}$ $M_{2}$ = 4 kg its displacements are obtained $ξ_{1} (\infty)$ $ξ_{1} (\infty)$ = 80 nm, $ξ_{2} (\infty)$ $ξ_{2} (\infty)$ = 20 nm, $ξ_{1} (\infty) + ξ_{2} (\infty)$ $ξ_{1} (\infty) + ξ_{2} (\infty)$ = 100 nm with error 10%.

For the transverse piezo engine at elastic‒inertial load the expression has the form

$W (s) = \frac{Ξ (s)}{U (s)} = \frac{d_{31} h / δ}{(1 + C_{l} / C_{11}^{E}) (T_{t}^{2} p^{2} + 2 T_{t} ξ_{t} p + 1)}$ $W (s) = \frac{Ξ (s)}{U (s)} = \frac{d_{31} h / δ}{(1 + C_{l} / C_{11}^{E}) (T_{t}^{2} p^{2} + 2 T_{t} ξ_{t} p + 1)}$

$T_{t} = \sqrt{M / (C_{l} + C_{11}^{E})}$ $T_{t} = \sqrt{M / (C_{l} + C_{11}^{E})}$ , $ω_{t} = 1 / T_{t}$ $ω_{t} = 1 / T_{t}$

where $C_{l}$ $C_{l}$ , $C_{11}^{E}$ $C_{11}^{E}$ are the stiffness of load and engine, $T_{t}$ $T_{t}$ , $ξ_{t}$ $ξ_{t}$ , $ω_{t}$ $ω_{t}$ are the time constant, the attenuation coefficient and the conjugate frequency of the engine. At M= 3 kg, $C_{l}$ $C_{l}$ = 0.2×10⁷ N/m, $C_{11}^{E}$ $C_{11}^{E}$ = 1×10⁷ N/m its parameters are determined in the form the time constant $T_{t}$ $T_{t}$ = 0.5×10^‒3 s and the conjugate frequency of the engine $ω_{t}$ $ω_{t}$ = 2×10³ s^‒1 with error 10%.

Conclusion

The structural model of a piezo engine for composite telescope is obtained. The structural model clearly shows the conversion of electrical energy by a piezo engine into mechanical energy of the control element of a composite telescope using the physical parameters of a piezo engine and its load. The structural scheme of a piezo engine for composite telescope is determined.

The matrix equation of a piezo engine is received for the calculation its displacements and parameters. The structural model, the structural scheme and the matrix equation of a piezo engine are used in decisions of the control systems for composite telescope.

Acknowledgments

None.

Conflicts of interest

None.

References

Schultz J, Ueda J, Asada H. Cellular Actuators. Butterworth‒Heinemann Publisher, Oxford, 2007, 382 p.
Afonin SM. Absolute stability conditions for a system controlling the deformation of an elecromagnetoelastic transduser. Doklady Mathematics. 2006;74(3):943‒948.
Uchino K. Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher. 1997;350 p.
Afonin SM. Generalized parametric structural model of a compound elecromagnetoelastic transduser. Doklady Physics. 2005;50(2):77‒82.
Afonin SM. Structural parametric model of a piezoelectric nanodisplacement transducer. Doklady Physics. 2008;53(3):137‒143.
Afonin SM. Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics. 2008;73(2):307‒313.
Cady WG. Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw‒Hill Book Company, New York, London, 1946;806 p.
Mason W, editor. Physical Acoustics: Principles and Methods. Vol.1. Part A. Methods and Devices. Academic Press, New York, 1964;515 p.
Y Yang, L Tang. Equivalent circuit modeling of piezoelectric energy harvesters. Journal of Intelligent Material Systems and Structures. 2009;20(18):2223‒2235.
Zwillinger D. Handbook of Differential Equations. Academic Press, Boston, 1989;673 p.
Afonin SM. A generalized structural‒parametric model of an elecromagnetoelastic converter for nano‒ and micrometric movement control systems: III. Transformation parametric structural circuits of an elecromagnetoelastic converter for nano‒ and micrometric movement control systems. Journal of Computer and Systems Sciences International. 2006;45(2):317‒325.
Afonin SM. Decision wave equation and block diagram of electromagnetoelastic actuator nano‒ and microdisplacement for communications systems. International Journal of Information and Communication Sciences. 2006;1(2):22‒29.
Afonin SM. Structural‒parametric model and transfer functions of electroelastic actuator for nano‒ and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Ed. Parinov IA. Nova Science, New York, 2015;pp. 225‒242.
Afonin SM. A structural‒parametric model of electroelastic actuator for nano‒ and microdisplacement of mechatronic system. Chapter 8 in Advances in Nanotechnology. Volume 19. Eds. Bartul Z, Trenor J, Nova Science, New York, 2017;pp. 259‒284.
Afonin SM. Electromagnetoelastic nano‒ and microactuators for mechatronic systems. Russian Engineering Research. 2018;38(12):938‒944.
Afonin SM. Nano‒ and micro‒scale piezomotors. Russian Engineering Research. 2012;32(7‒8):519‒522.
Afonin SM. Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids. 2007;42(1):43‒49.
Afonin SM. Stability of strain control systems of nano‒and microdisplacement piezotransducers. Mechanics of Solids. 2004;49(2):196‒207.
Afonin SM. Structural‒parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics. 2017;5(1): 9‒15.
Afonin SM. Structural‒parametric model multilayer electromagnetoelastic actuator for nanomechatronics. International Journal of Physics. 2019;7(2):50‒57.
Afonin SM. Calculation deformation of an engine for nano biomedical research. International Journal of Biomed Research. 2012;1(5):1‒4.
Afonin SM. Precision engine for nanobiomedical research. Biomedical Research and Clinical Reviews. 2012;3(4): 1‒5.
Afonin SM. Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano‒ and microdisplacement. International Journal of Mathematical Analysis and Applications. 2016;3(4):31‒38.
Afonin SM. Structural‒parametric model of electromagnetoelastic actuator for nanomechanics. Actuators. 7(1):1‒9.
Afonin SM. Structural‒parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators. 2019;8(3):1‒14.
Afonin SM. Structural‒parametric models and transfer functions of electromagnetoelastic actuators nano‒ and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics. 2016;2(2):52‒59.
Afonin SM. Design static and dynamic characteristics of a piezoelectric nanomicrotransducers. Mechanics of Solids. 2010;45(1):123‒132.
Afonin SM. Electromagnetoelastic actuator for nanomechanics. Global Journal of Research in Engineering: A Mechanical and Mechanics Engineering. 2018;18(2):19‒23.
Afonin SM. Multilayer electromagnetoelastic actuator for robotics systems of nanotechnology, Proceedings of the 2018 IEEE Conference EIConRus, 2018;pp. 1698‒1701.
Afonin SM. A block diagram of electromagnetoelastic actuator nanodisplacement for communications systems. Transactions on Networks and Communications. 2018;6(3):1‒9.
Afonin SM. Decision matrix equation and block diagram of multilayer electromagnetoelastic actuator micro and nanodisplacement for communications systems. Transactions on Networks and Communications. 2019;7(3): 11‒21.
Afonin SM. Condition absolute stability control system of electromagnetoelastic actuator for communication equipment. Transactions on Networks and Communications. 2020;8(1): 8‒15.
Afonin SM. A Block diagram of electromagnetoelastic actuator for control systems in nanoscience and nanotechnology. Transactions on Machine Learning and Artificial Intelligence. 2020;8(4):23‒33.
Afonin SM. Optimal control of a multilayer electroelastic engine with a longitudinal piezoeffect for nanomechatronics systems. Applied System Innovation. 2020;3(4): 1‒7.
Afonin SM. Coded сontrol of a sectional electroelastic engine for nanomechatronics systems. Applied System Innovation. 2021;4(3): 1‒11.
Afonin SM. Structural scheme actuator for nano research. COJ Reviews and Research. 2020;2(5):1‒3.
Afonin SM. Structural–parametric model electroelastic actuator nano‒ and microdisplacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences. 2018;3(5): 306‒309.
Afonin SM. Electromagnetoelastic actuator for large telescopes. Aeronautics and Aerospace Open Access Journal. 2018;2(5): 270‒272.
Afonin SM. Structural‒parametric model actuator of adaptive optics for composite telescope and astrophysics equipment. Physics & Astronomy International Journal. 2012; 4(1):18‒21.
Afonin SM. Calculation of the deformation of an electromagnetoelastic actuator for composite telescope and astrophysics equipment. Physics & Astronomy International Journal. 2021;5(2):55‒58.
Afonin SM. Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surgery & Case Studies Open Access Journal. 2019;3(3):307–309.
Afonin SM. Piezo actuators for nanomedicine research. MOJ Applied Bionics and Biomechanics. 2019;3(2): 56‒57.
Afonin SM. Frequency criterion absolute stability of electromagnetoelastic system for nano and micro displacement in biomechanics. MOJ Applied Bionics and Biomechanics. 2017;3(6):137‒140.
Afonin SM. Multilayer piezo engine for nanomedicine research. MOJ Applied Bionics and Biomechanics. 2020;4(2):30‒31.
Afonin SM. Multilayer engine for microsurgery and nano biomedicine. Surgery & Case Studies Open Access Journal. 2020;4(4):423‒425.
Afonin SM. Rigidity of a multilayer piezoelectric actuator for the nano and micro range. Russian Engineering Research. 2021;41(4):285‒288.
Afonin SM. A structural‒parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in Nanotechnology. Volume 22. Eds. Bartul Z, Trenor J, Nova Science, New York, 2019;pp. 169‒186.
Afonin SM. Electroelastic digital‒to‒analog converter actuator nano and microdisplacement for nanotechnology. Chapter 6 in Advances in Nanotechnology. Volume 24. Eds. Bartul Z, Trenor J, Nova Science, New York, 2020;pp. 205‒218.
Afonin SM. Characteristics of an electroelastic actuator nano‒ and microdisplacement for nanotechnology. Chapter 8 in Advances in Nanotechnology. Volume 25. Eds. Bartul Z, Trenor J, Nova Science, New York, 2021;pp. 251‒266.
Nalwa HS, editor. Encyclopedia of Nanoscience and Nanotechnology. Los Angeles: American Scientific Publishers. 2004.
Bhushan B. Springer Handbook of Nanotechnology. New York: Springer, 2004;1222 p.