In the Standard Model (S.M.), it is known the constituent quark model, with a valence current quark (u-up, d-down, s-strange) or (c-charm, b-bottom, t-top) with a current mass:1 (1.8¸2.8; 4.3¸5.2; 92¸104) MeV/c2, respective: (1.27; 4.18; 173) GeV/c2 and a gluonic shell formed by gluons and sea-quarks,1 the resulted effective quark mass being the constituent quark mass: (336, 340, 486) MeV/c2, respective: (1.55, 4.73, 177) GeV/c2. The electric charge of u-, c-, t- quarks is +(2/3)e and the electric charge of d-, s-, b- quarks is –(1/3)e, the strong interaction of quarks being explained by so-named “color charge”, the gluons having two opposed color charges, the gluon field between a pair of color charges forming a narrow flux tube (as a ‘string’) between them, (the Lund string model).2 However, the Grand Unified theories (GUT) predict relations among the fermion masses, such as between the electron and the u-, d-quark, the muon and the strange quark and between the tau lepton and the bottom quark, but these relations were only partially obtained.
In a Cold Genesis pre-quantum theory of particles and fields, (C.G.T.,),3-5 based on the Galilean relativity, it results as more natural alternative the possibility to explain the constituent quarks and the resulted elementary particles as clusters of negatron-positron pairs, named ‘gammons’
, resulting that preonic bosons and quarks can be formed also ‘at cold’, as Bose-Einstein condensate of ‘gammons’ which form quasi-stable basic preons z0 of mass ~34 me , forming constituent quarks, (M. Arghirescu, 2006, p. 58).3 This z0 -preon was deduced by calibrating the value:
obtained by Olavi Hellman,5 by using the masses of the proton and of the
-baryon.3
The Olavi Hellman’s relation was deduced by a system of non-linear classical field equations having particle-like solutions, this relation being obtained in the form:
(1)
In a relative recent paper, (2015),7 after some experiments for the detection of dark photons, a research team of Science’ Institute for Nuclear Research in Debrecen (Hungary) evidenced a neutral super-light particle with a mass of ~17 MeV/c2 , (~34 me), named X17, by a reaction:
,
which was explained in CGT by the conclusion that z0-preon is composed by two ‘quarcins’, c0±, its stability being explained in CGT by the conclusion that it is formed as cluster of an even number n = 7x6 = 42 quasielectrons, (integer number of degenerate “gammons”,
), with mass me*
, i.e. reduced to a value corresponding to the charge e* = ±(2/3)e by a degeneration of the magnetic moment’s quantum vortex
, given by ‘heavy’ etherons of mass
and ‘quantons’ of mass
. The considered “gammons” were experimentally observed in the form of quanta of “un-matter” plasma.8
The me* -value results in CGT by the conclusion that the difference between the masses of neutron and proton:
is given by an incorporate electron with degenerate magnetic moment and a linking ‘gammon’
, forming a ‘weson’,
, which explains the neutron in a dynamide model of Lenard- Radulescu type,3 (protonic center and a negatron revolving around it by the
-vortex with the speed ve* << c, at a distance
fm4- close to the value of the nucleon’s scalar radius:
fm used by the formula of nuclear radius:
), at which it has a degenerate
-magnetic moment and Sen –spin).
The degenerate value
of the magnetic moment of a protonic positron (giving its charge, as in the Anderson’s model) or of a quasielectron results in CGT by the decreasing of its Compton radius
proportional with the quantum density
of the protonic Np- cluster in which is placed the electron’s super-dense kernel, (its centroid), from the value:
, to the value:
, (virtual radius of the proton’s magnetic moment
) given by the quantum mean density increasing, from the value:
to the value:
; (
;
– the mean density of electron and nucleon).
The used electron model supposes an exponential variation of its density, given by photons of inertial mass mf , vortically attracted around a dense kernel m0 and confined in a volume of classic radius a = 1.41 fm, (the e-charge in electron’s surface), the superposition of the (Np+1) quantonic vortices,
, of the protonic quasielectrons, generating a total dynamic pressure:
, inside a volume with radius: da = 2.1 fm, which gives an exponential nuclear potential:
of eulerian form conform to :
,(2)
with:
and
(0.6fm)-the ‘impenetrable’ volume,3,9 the nucleon resulting as formed by
quasi-electrons which give a proton density in its center of value:
,
, giving- with
:
and:
– value specific to the mean binding energy per nucleon in the nuclei with the most strongly bound nucleons, (9.14 ¸9.15 MeV/nucleon for 56Fe, 58Fe, 60Ni, 62Ni), explained by the Bernoulli’s law.3
In CGT it was also deduced a quark model of cold forming quark, with effective (constituent) mass giving the particle’s mass by the sum rule, by considering as fundamental stable sub-constituent the basic preon
which can form derived “zerons”, (preonic neutral bosons:
, the light and semi-light quarks (mqc2 < 1 GeV) resulting by only two preonic bosons: z2(4z0) = 136 me and:
.
The cold quarks result as superpositions of preonic bosons z2 = 4z0 and
with almost the same symmetry (Figure 1), resulting a constituent quark’ mass equation:4,5
(3)
i.e:
, (‚mark’ –mesonic quark);
, (‚rark’- un-stable quark);
(park, nark –nucleonic quarks); (lark –lambda-quark);
(sark –strange quark);
(vark).
The values of the basic quarks m1,2 (‚mark’,)3,4 are m1+ = 135.2 me and m2- = 137.8 me and correspond to a mean value
obtained by Eq. (1) with l0 = a = 1.14 fm, (electron’s classic radius corresponding to the e-charge contained by its surface), so:
.
The particle’s mass results by eqs. (3), in the approximation of the sum rule applied to the particle’s cold forming, as consequence of the quantum fields’ superposition principle applied to the particle’s cold forming as sum of degenerate electrons, whose total vortical field can explain also the nuclear force
conform to eq. (2).3,9
The main link between CGT and the S. M. consists in the fact that- considering the electron’s mass confined in its kernel, the z0-preon can be considered as formed by 3 pairs
of current uc -quarks formed by a quasielectron (e*±) surrounded by 3 gluonic ‘gammons’, i.e. with mass:
, the current d-quark resulting with a mass:
, (in the limits accepted by S.M.).
M. de Souza10 deduced the energy levels of baryon resonances with maximal discrepancy of ~5% by a rest mass’ energy of constituent quarks (Eq = mqc2) taken as being:
, Eq(ms) = 0.5 GeV, Eq(mc) = 1.7 GeV, Eq(mb) = 5 GeV, Eq(mt) = 174 GeV, (u, d- up, down; s, c- strange, charm; b, t –bottom, top).
A selection rule for the heavy quarks masses, which- with high discrepancy, may be applied also for the values used by de Souza (which are close to but higher than those used by the Standard Model,
) was found by R. A. Carrigan Jr.11 which found an exponential formula for the heavy quark masses:
and
, (values used by the Standard Model of the Quantum mechanics), of the form:
(4)
Eq. (4) being explained by the forming of compound quarks with upper mass as tri-quark combinations, i.e- as triplets formed by quarks with adjacent lower mass,
: two paired quarks
and an un-paired quark giving the charge and the magnetic moment.
By a z0-preon with a ratio: length/diameter
, it results in CGT that the cold quark’s stability is given by the (quasi)crystalline arrangement of its cluster of preonic kernels (kerneloids’)12 of regular hexagonal polyhedron form, with the ratio: length/diameter = 1÷2, i.e.- with 3÷5 levels of preonic bosons
and/or z2(4z0) and a light m1;2 -quark resulting from a z2-boson by the loosing of a degenerate electron e*.
By the principle of similitude, it results that a similar (quasi)crystalline arrangement may result by kernels of (semi)light quarks (mq < 1GeV/c2) or of heavy quarks (c- or b-quarks), formed as composite quarks by some (q-`q)-pairs and a un-paired q± -quark, also in the form:
.
It was shown by author12 that the values ms, mc and mb used by de Souza10 and those used by the S.M.1 can be deduced by the CGT’s model, with eq. (10), by the next observations:
-
-the mass of the nucleonic quarks of CGT;
-
-the mass of s-quark;
- mc = 1.7 GeV/c2 = 3326.8 me –charm quark’s mass used by de Souza, and:
- mb = 5000 MeV –bottom quark’s mass used by de Souza,
were obtained in CGT by eq. (4), by taking:
(-the mass of v-quark of CGT, instead of ms), and by considering the quarks c(mc+) and b(mc-) as de-excited states of the triplet with mass: m4*= m(c*) = 3mv*(v+) = 3363.6 me, (1.718 GeV/c2), and respective:
, (q* -‘cold’ quark), by the next de-excitation reaction:
(5a)
(5b)
- The t-quark results as collapsed cluster:
the structure of its kernel resulting by similitude with the preonic structure of the s-quark as formed from a pre-cluster of regular hexagonal polyhedron form with length/diameter
, in acceptable concordance with the experimentally obtained value of its constituent mass (
13 p. 135), with upper stability given by the crystalline form of its current mass, formed by kernels of b-quarks,12 the forms:
h0 = (7x3)m(c)= 35.7 GeV/c2 and (7x5)m(c) = 59.5 GeV/c2 resulting also as possible.
- The quarks
used by the S.M. result from the CGT’s quarks: s- , c+ , b- by the reactions:
(6a)
(6b)
(6c)
- If we interpret the energy:
, loosen at the de-exciting of the quarcic cluster qck+1, as binding energy between quarks, (by similitude with a nucleus), it may be obtained a semi-empiric relation for the mass of the heavy quarks
and
:
(7)
with: m1 = mv = 0.574 GeV/c2 ; z0 = 17.374 MeV/c2, (34 me) and ln(3n-13n-2) = ln32n-3 , which gives:
A relative similar semi-empiric relation may be found also for the quarks
and
, of the S.M., but in the form:
(8)
with:
giving:
the expression (8) being characteristic to mass addition to the tri-quark cluster, as in the case of the Sakharov’s equation,14 (which adds a term of spin-spin interaction at the total mass of quarks).
Quarks ‘species’ identifiable in CGT
From the previous equations it results that it is possible to classify the quarks obtained in CGT as being of two types (‚species’):
-A-species: preonic quarks -composed by the preonic bosons z2 = 4z0 and
, with mass mq(qA) given by Eq. (3) -, which are characteristic mainly to astro-particles;
-B-species: quarkonic quarks (composed of lighter quarks with or without de-excitation reaction),
with two sub-species:
- B1 –tri-quarcic, composed of 3n preonic quarks (mainly –v- or/and s-quarks) with 4 ³ n ³ 1,
(with mass mq(qB1) given by Eqs. (7) and (8)), and:
- B2 –multi-quarcic (with mass mq(qB2) given by: mq(qB2) = (7x5)mq(qB1) with theoretically possible variant:
),
(i.e. composed of preonic quarks).
The fact that the preonic quarks qA and qB1 can explain the ground states of the heavy elementary particles (mainly-heavy mesons and heavy baryons) by two mass ‚flavors’: of S.M. type and of Souza/CGT type, (Eqs. (6), (7), (8)) can be explained by the conclusion that the ‚flavor’ fq = f1 = 1 (of S.M.’s type) corresponds- for B-species, of composite quasi-stable quarks
generated in a strong interaction between lighter quarks (qk-1), at high impact energy, corresponding to a higher mass difference
between the sum of the qA –quarks which compose the composite qB1 –quark and the mass of the formed qB1 –quark, and the second ‚flavor’ (fq = f2 = 2 -of Souza/CGT type) corresponds to meta-stable quarks (qks) generated in a semi-strong interaction between lighter quarks (qk-1).
- -For qA –quarks of A-species, the general equation for the effective (constituent) quark mass, is:
(9)
The values k = 0; n = 0 correspond in CGT to the basic (mesonic) quark m±, (‚mark’).
For k = 3, n = 1, f = 1 is retrieved the mass of the
-quark (of the S.M.):
±(483) = s±(500) - z0 .
- -For the sub-species B1(qB1), by Eqs. (7), (8), assimilating the difference
with a binding energy lost in the formation of the composite quark
or qks, we can obtain a semi-empiric general equation for the quark’s effective mass m(qnc) by considering the flavors numbers: fq = f1 = 1;
fq = f2 = 2 and that both flavors of composite quarks: qns and
are obtained from ‚cold’ v-quarks:
i.e. by taking in Eq. (8):
(10)
It results, from Eqs. (7) , (8), (10), with: m1 =mv(574MeV), that:
(11)
(12)
The resulting general equation for m(qnc), for quarkonic quarks qnf = qB1 , is- in consequence:
(13)
or:
(13')
Eq. (13), by
Eq. (7) for m(qns) and by f = |fq| = 1 it retrieves Eq. (8) for
.
The mass difference
is characteristic –in consequence, to fq = 1, (strong interaction, at high energies) and it is approximately equal to the mass of the preonic boson z1(3z0) = 52.1 MeV. However, theoretically is not excluded the possibility to take in Eq. (13’), the value: m1 = ms(504MeV) or
, corresponding to a cold quark‚ (sark or lark), of CGT. From the Annexes C and D of Ref.15 it results that a de-excitation reaction with emission of z1 –boson can explain the ground states of the majority of baryons with total spin: Jp = 3/2. The conserving of the total‚ flavor’ number imply the conclusion that the flavor of
for quarks and
, at the anti-quark’s transforming, because we must take:
.
- -For the sub-species B2(qB2), by the formula:
m(qnc)B2 = (7x5)m(qn-1); (14)
(or simply: mn = (7x5)mn-1)
it results the next possible variants:
The last variant, obtained with qn-1= b, corresponds to the top quark, (effective mass mt = 177GeV/c2).
A general equation for the mass of baryons and of mesons, obtained by CGT
By analysing the Annexes A- D of Ref.15 it results that:
- -for baryons:
-almost all baryons with total angular momentum (total spin) Jp = ½ result from quarks of flavor fq = 1, (of Souza/CGT type), by the sum rule or with a de-excitation reaction corresponding to the loosing of (1¸2) z0 –preons, excepting the case of
(3.621) which results as composed by
- quarks of fq = 2, (of S.M. type), or as triplet: (ccp) or (ccn) de-excited by emission of 5z0.
- the baryons with total spin Jp = 3/2 results from quarks of flavor fq =1, by de-excitation reaction with emission of at least one z0-preon, generally –of three preons (one z0-preon/constituent quark)- corresponding to a z1 bosonic preon, or with emission of a z2(4z0) or z3(6z0) –preonic boson, excepting four cases, of:
whose mass results as sum of the masses of their constituent quarks –indicating a weaker (semi-strong) interaction between these quarks at the baryon’s forming.
A general semi-empiric equation for the baryons’ mass can be written in this case in the form:
(15)
(f = fq = 2; n = 0¸2 for Jp = ½ and n = 0¸5 for Jp = 3/2);
(fq –quark’s flavor).
Conform to Eq. (15), the baryon:
(3.621) corresponds to Jp = 3/2 and n = 4.
The mass defect
represents generally less than 2.7% of the particle’s mass mass, (excepting
(1532), resulting as: [(λvv) –z1], for which
corresponding to Jp = 3/2; n =2).
Conform to Eq. (15), the baryons which were formed without mass defect, (with
), are considered with Jp = ½ .
- For heavy mesons:
-by analysing the Annexes A- B of Ref.15 it results that the heavy mesons may be explained as pairs
by considering the both variants of the charm and of the bottom quarks:
(the Souza’s and the S.M.’s mass variants), i.e. with flavor fq = 2 or fq = 1, the pair of heavier quarks being de-excited by a defect mass dm corresponding to the emission of a preonic boson zk = n×z0 with
and which is generally of higher value to the formed pseudo-scalar mesons than to the formed vector mesons.
Because the pseudoscalar mesons have the total angular momentum (total spin) Jp = 0 and the vector mesons have Jp = 1, it can be written a semi-empiric equation similar to Eq. (15) but considered for
, in the form:
(16)
So, all mesons which can be explained by a reaction of the form (16), by combinations
, are in concordance with the CGT’s model.
Arguments for a vortical model of electron and a multi-vortical model of meson and baryon
The stability of the vector photon and of the electron’s magnetic moment
According to the vortical model of electron, of vector photon and of magnetic field, an electron and a free
vector photon must have also a perpetual ‘quantonic’ vortex Gv which gives its magnetic moment and – in the case of the lightest vector photons- also its spin. It was shown in CGT16 that for the case of a single ‚quanton’, of mass mh = h×1/c2 and radius rh , it results that its maintaining on the vortex line lr = 2pr around the super-dense centroid of radius r0 of a vector photon or of an electron, is possible by an etheronic force Fsh of Magnus type given by the quanton’s passing with the speed
through a brownian etheronic medium of variable density
, caused by the electron’s or the vector photon’s etheronic vortex
of heavy etherons’ (‚sinergons’ –with mass
)5 having an impulse density:
, the induced etheronic
- vortex of the quanton, of circulation:
, being explained by the gradient
of the relative impulse density ps of etherons related to the quanton’s surface, maintained by etheronic winds.17 A similar gradient,
of the
–vortex, generates a
- vortex to pseudo-stationary quantons which are attracted towards the vecton’s center. The condition of the quanton’s maintaining on the vortex-line is given by the dynamic equilibrium equation:
(17)
with:
- the density of sinergons’ at the surface of the vector photon’s or the electron’s centroid, by considering the quanton as cylindrical, of lenght lh = 2rh and density rh.17 This dynamic equilibrium (17) is realized by the resulted condition:
i.e. –by the condition:
.
With the value resulting from Ref.3 for the ratio:
, (giving rh = 1.79x10-25m), it results:
(18)
[kg/m2].
The quanton’s c-speed can be maintained by a dynamic equilibrium of etheronic pressure forces Ft on the tangent direction, of Stokes type
, given by the
–vortex having a density
and by the density
which generates a drag force:
.
The justification for the conclusion that the interaction of the etheronic fluid composed by ‚heavy etherons’ (‚sinergons’) with an un-bound quanton is in the laminary regime (specific to the Stokes type force) is the fact that the Reynolds number:
is still low also in this case because- even if
and the kinematic viscosity
of the medium of heavy etherons must be low, the specific lenght L must be approximately the diameter of the quanton, in this case, so –very small,
However, for the interaction of bound quantons with a flux of gravitonic etherons (
)18 we can consider the turbulent regime, (characterized by Navier-Stokes equations, with
), the kinematic viscosity of the flux of gravitonc etherons being lower than that of the‚ heavy etherons’ medium, (the medium of gravitonic etherons –much smaller than the sinergons, being more super-fluid).
By the hypothesis that the etheronic force Fa on the tangent direction is of Stokes type, specific to a laminary flowing of the etheronic medium, at dynamic equilibrium we have:
(19)
(20a)
(20b)
Particularizing for the case of the electron’s magnetic moment vortex,
, for which Ref.3 gives a density:
(a = 1.41 fm), and by using the formula:
for the electron’s B-field,3 with vv = c for
, by using for the magnetic potential the relation obtained in CGT,3 it results that :
(21a)
(21b)
By taking:
,3 it results:
From Eq. (20) we have also:
, resulting that:
, i.e.- a value which corresponds to the used hypothesis that the magnetic moment of electrons and of vector photons is given by an etherono-quantonic vortex induced by etherono-quantonic winds. For
, (value corresponding to a density of 3.6x1019 kg/m3 of the inertial mass
of a vector photon),3 by Eq. (18) we obtain:
, (with one size order of magnitude higher than the nucleon’s density). By Coandă effect, an etheronic vortex (but of gravitonic etherons) and an etheronic force of Magnus type can explain the stability of the sinergonic vortex ΓA which –in CGT, explains the observed physical nature of the magnetic potential A of the electron’s magnetic moment.
The perpetual rotation of the atomic electrons
It is know that the persisting currents in a superconductor, which flow at the superconductor’s surface to oppose the applied field and which expel the magnetic field of an external magnet, are not a result of Lenz's Law or Faraday's Law, (are not induced by change in flux), and that they do not decay with time, giving the illusion of perfect diamagnetism. Conform to CGT, we may suppose that the etheronic (‘sinergonic’)
–vortex associated to the A-potential which induces the magnetic vortex-tubes
of the magnet’s B-field, can maintain the intensity of the persisting current of electrons and of electronic Cooper pairs in a supraconductor, by its dynamic (etheronic) impulse density:
conform to a dynamic equilibrium equation (19), (20) multiplied by a fa- factor (fa <<1) imposed by the superfluidity of the etherono-quantonic medium (in which the drag force tends to zero). A similar but nuclear
–vortex can explain the perpetual rotation of the atomic electrons, in CGT.3 In the case of the hydrogen atom- for example, the quantified electron’s speed: ve(rn) = ve0(r0)/n, (rn = n2r0; n = 0, 1, 2…), gives the variation law:
which can be explained by a equation of dynamic equilibrium on the direction tangent to the electron’s rotation:
(22)
with:
- impulse density of the etherono-quantonic vortex
of the nuclear proton’s magnetic moment,
and:
the equivalent density of the low frictional Brownian (etherono-quantonic) medium which generate a drag force FR of Stokes’ type.
The expression of
in Eq. (22) results by correspondence with Eq. (20) at least for r = 2a. The coefficient
is imposed by the exponential variation of the quantonic density given by the superposed
- vortices of the proton’s cluster of degenerate electrons in the volume of radius r = 2a, (a = 1.41 fm), with their kernels confined in a protonic ‚impenetrable’ quantum volume of radius
.3,4
For: r = 2a ,
with
we have:
(23)
(with:
-the sinergonic vortex
resulting as pseudo-vortex with w- quasi-constant). It is observed that the speed of a beta radiation’s electron (~0.92c) is obtained (Eq. (23)) for: r = 2a.
For r >> a, (i.e. –for the case of an atomic electron), because in this case ve << c, we have:
(24a)
(24b)
It can be shown that –without the‚ sinergonic’ vortex of the atomic nucleus’ magnetic moment, because the density of the etherono-quantonic component of the‚ zero point’ energy of the quantum vacuum, the atoms would have a relative short existence, because the‚ drag force’ FR generated by this medium would determine the loosing of the electron’s kinetic energy and its falling to atomic nucleus. For a released electron at the neutron’s beta transforming, but also for quantons of the nuclear proton’s magnetic moment:
, (
–the nuclear magneton), corresponding to a Compton radius:
(ri –theoretic radius of the proton’s impenetrable quantum volume), Eq. (23) of dynamic equilibrium gives vh = c (until) at the limit: rlp = 2.35 fm and it is explained by the coefficient
, i.e. by the Compton radius of the photons contained in the proton’s quantum volume, which decreases from the value:
–specific to a photon contained by the electron’s volume, to the value:
–for the photons contained in the proton’s surface, of theoretic scalar radius
, (rle extending the protonic volume with quantons circulated at vct = c, to one of radius:
,
and
- being the electron’s mean density and the density of the proton’s surface, considering an exponential decreasing of its density.3 The apparent contradiction between the obtained values rlp = 2.35 fm and
is solved in CGT by a semi-empiric relation for the quantons’ speed in the vortex
of the proton’s magnetic moment, of the form:3
(25)
which - for r >> rlp , gives:
which retrieve the classic expression of magnetic induction by the CGT’s formula, with a variation of the density of quantons:
i.e.:
(26)
It exist a phenomenon named "cryogenic electron emission," that has no known physics explanation. At very cold temperatures, in the absence of light, a photomultiplier will spontaneously emit single electrons. The phenomenon was first observed nearly 50 years ago. The electrons are emitted in bursts distributed randomly in time. As the temperature decreases, the rate of bursts, as well as the number of events per burst, increase. Although scientists know of a few causes for electron emission without light (also called ‚the dark rate’), including heat, electric field and ionizing radiation - none of these can account for cryogenic emission.19 It can be observed that this phenomenon is in concordance with the vortical atomic model, i.e. with the conclusion that the atomic electrons are rotated under the pressure force generated by a vortex of heavy etherons of the magnetic potential A which generate the B-field of the nuclear magnetic moment, which acts more efficient over the electrons of an un-vibrated atom, (at lower temperatures).
Theoretic implications in astrophysics of a (multi)vortical model of nucleon
Arguments for a ‘gravistar’ model
An important theoretic consequence of the (multi)vortical model of quark and of elementary baryonic particle, of CGT, (particularly-nucleon), is a ‘gravistar’ model,3 conceived as a hard-core rotation ellipsoid of “dark energy” with vortexially generated “dark photons” and “dark particles” formed as Bose-Einstein condensates at distinct levels of density.
This gravistar model was inspired by the model of “gravastar”proposed by Mottola and Mazur20 with very cold core with central “black hole” and a “dark energy” fluid which may create Bose-Einstein condensate in the outer core, and a thin shell of matter on the events horizon, the dark energy-like behavior of the inner region preventing the collapse to a singularity and the presence of the thin shell preventing the formation of an event horizon, avoiding the infinite blue-shift. Also, the inner region of this gravastar has thermodynamically no entropy and may be thought of as a gravitational Bose–Einstein condensate.
In the model of hard-core gravistar proposed in CGT,3 a region of vortexed elementary particles, plasma and photons can exists inside an ellipsoidic region of “dark” etherono-quantonic enery, forming a relativist etherono-quantonic vortex:
, with the etheronic part formed by heavy etherons (sinergons’) generating the magnetic potential A of a strong (magnetaric) magnetic B-field generated by the magnetic moment
of a rotated hard-core, similarly to the electron case. This gravistaric hard core (HC) of mass MC must be a black hole but in the sense that at least the quantons
and‚ trapped’ vector photons are maintained on circular orbit around the gravistaric hard core by a quantum potential
generated by a force FM(r) of Magnus type, which satisfy the stability condition conform to Eqs. (19)-(22), (and not purely gravitational- in this case), the pseudo-scalar photons of mass
, speed
and density
of the inertial mass of its vector photons, (formed as couple of vector photons with opposed spins and magnetic moments –in CGT),17 being retained when the sum between the gravitation potential Vg(r) and the gravito-magnetic potential
(conform to Eq. (2)), (given by the static pressure Ps(r) of the pseudo-stationary etheronic medium of heavy etherons gravitationally accumulated around the gravistaric hard core), becomes equal to the centrifugal potential, i.e.:
(27)
The magnetic field B of a gravistar can be generated- as in a black-hole’s case, by the charged plasma of a rotated accretion disk or/and the electric charge of the rotated HC, (or –low probable, and by its permanent magnetization). Also, if HC is a spinning black hole, it can generate matter
energy conversion in the known mode, destroying nuclear matter and releasing polar relativist jets of radiation and elementary particles.
- It is known in this sense that spinning black holes with accretion disks are thought to generate very strong magnetic fields, which are presumably responsible for the astrophysical jets that have been observed in several systems.21 Relativistic jets are beams of ionized matter accelerated close to the speed of light. Most have been observationally associated with central black holes of some active galaxies, radio galaxies or quasars, and also by galactic stellar black holes, neutron stars or pulsars. Massive central black holes in galaxies have the most powerful jets, but their structure and behaviors are similar to those of smaller galactic neutron stars and black holes. These systems are often called microquasars’. Relativistic jets formation may also explain observed gamma-ray bursts. But the mechanisms behind the composition of jets remained uncertain. Some studies favor models where jets are composed of an electrically neutral mixture of nuclei, electrons, and positrons, while others are consistent with jets composed of positron–electron plasma, as in case of quasars 3C278 and 3C345.22
About 1% of supermassive black holes have an "accretion disk" of gas and dust swirling around them. When material from this disk falls toward the black hole, it gets so hot that it shines more brightly than the whole rest of its galaxy. One in 10 of these active black holes also produces jets that fire out particles at 99.995% of the speed of light. Astrophysicists suspect that accretion disks produce the jets, but they don't know how. The researchers chose for its association with a natural cosmic lens. Schild and his colleagues23 found that for the quasar Q0957+561 the jets appear to emerge from two regions of 1,000 astronomical units in size located above the poles of the central compact object, and that location would be expected only if the jets were powered by reconnecting magnetic field lines that were anchored to the rotating supermassive compact object within the quasar. It was concluded that by interacting with a surrounding accretion disk, such spinning magnetic field lines spool up, winding tighter and tighter until they explosively unite, reconnect and break, releasing huge amounts of energy that power the jets, this magnetic field being internally anchored to a central, rotating supermassive black hole, the inner edge of the accretion disk, located about 2,000 astronomical units from the central object, being heated to incandescence by the swirling, internal magnetic field, pulled around by the rotation of the central compact object, ("magnetic propeller effect").
Observations also suggest the presence of a broad cone-shaped outflow from the accretion disk. The surprisingly large angular opening of the outflow that is observed is best explained by the influence of an intrinsic magnetic field contained within the central compact object in this quasar. With Kerr’s equations, Blandford and Znajek showed24 that when magnetic field lines from the accretion disk fall onto the spinning hole, the black hole’s rotation will wind the field lines into a helix oriented along the hole’s rotation axis, for the most part of its matter the disk being locked in place, (“magnetically arrested disk” or MAD models). Because the magnetic fields in motion generate E-field, a current of electrons and positrons will start flowing through the helix away from the black hole in both directions, forming the jet. But in light of the previous observations, Schild and his colleagues23 have proposed a controversial theory that the magnetic field is intrinsic to the quasar's central, supermassive compact object, rather than only being part of the accretion disk, proposing the name- Magnetospheric Eternally Collapsing Objects, (MECOs) and concluding that in addition to its mass and spin, the quasar's central compact object may have physical properties more like a highly redshifted, spinning magnetic dipole than like a black hole. For that reason, most approaching matter does not disappear forever, but instead feels the motor-like rotating magnetic fields and gets spun back out.
According to this theory, a MECO does not have an event horizon, so any matter that is able to get by the magnetic propeller is gradually slowed down and stopped at the MECO's highly redshifted surface, with just a weak signal connecting the radiation from that matter, but that signal is very hard to observe.23 This explanatory hypothesis is in concordance with the fact that Black holes become electrically charged when charged particles falls into them, up to an “extremal limit,” a saturation point where they store as much electric charge as possible for their size.
- By the vortical model of magnetic field used in CGT,3 the previous hypothesis is in concordance with the proposed model of gravistar.
-Also, because in the polar zones the radial speed of these emitted jets are less affected (diminished) by the dynamic pressure
of the etherono-quantonic vortex
of the HC’s magnetic field, the fact that these spinning black holes can emit relativist jets, by the resulting gravistar model it can be explained.
-It is also considered that four years of observations from the European Space Agency’s Integral (INTErnational Gamma-Ray Astrophysics Laboratory) satellite have cleared up the origin of a giant cloud of antimatter surrounding the galactic center of Milky Way, by observing a glow of 511 keV gamma rays from electron-positron annihilation. It was concluded that hard low-mass X-ray binaries, since they light up in high-energy (hard) X-rays as gas from a low-mass star spirals into a companion black hole or neutron star, they are producing significant amounts of positrons .
But scientists don’t understand how low-mass X-ray binaries could produce enough positrons to explain the cloud, and they also don’t know how they escape from these systems.25
- It can be observed that the quark model of CGT, resulting as Bose-Eistein condensate of ‚gammons’- considered as pairs of degenerate electrons:
which –logically, are released in the matter energy conversion process, can explain the considered composition of the emitted relativist jets, consisting in electrons, positrons, electron-positron pairs and gamma quanta.
The gravistar as source of dark energy
The Universe’ expansion is considered as caused by the ‚dark energy’ of the cosmic space. In CGT,3 in concordance with some astrophysical observations,26 this energy is an etheronic field-like component of the quantum vacuum; similar etheronic un-compensated fluxes can explain the gravitation force as in the Fatio-Lesage theory.3,18 A 32-year-old hypothesis of the formation of barred-spiral galaxies (Bostick 1957, 1958, 1986; Laurence, 1956 ) which become coherent-self-exciting homopolar generators has recently gained confirmative support from 3-D, particle-in-cell computer simulations.27 According to this model, such galaxies should be able to convert an appreciable fraction, f, of the energy from their gravitationally-collapsing plasmas to coherently-increasing magnetic energy via their coherent, self-exciting, homopolar-generator action. The following simple calculation shows that the resulting mutually-induced magnetic repulsions (Lenz's law) between neighboring galaxies is greater than the gravitational attractive forces between the galaxies. It was concluded that the observed expansion of the Universe can be thus simply accounted for, without recourse to the ‘Big Bang’ hypothesis.27 But the existence of the dark energy could explain and other astrophysical observations.
-It was also concluded that the supermassive black holes in elliptical galaxies are between seven and 20 times more massive than they were nine billion years ago.28 This indicates that supermassive black holes can gain mass through some other mechanism as well. And if they contain vacuum energy, they would both contribute to the expansion of the universe and gain mass from the process as well, in a phenomenon called‚ cosmological coupling’.
The researchers considered that this is the first observational evidence that black holes contain vacuum energy, and when they crunched the numbers they found that this could account for the amount of the dark energy measured in the universe today, (around 68%). While there’s been no shortage of other proposed sources of dark energy, this conclusion doesn’t require anything new to be added to our existing models – the gap can be plugged by black holes as predicted by Einstein’s general theory of relativity. The new model also explains another cosmological puzzle: In current models black holes are theorized to compress everything that falls into them into an infinitely dense singularity, a point where the laws of physics break down. This should be mathematically impossible. But if black holes contain vacuum energy, singularities no longer need to exist.
- The team compared observations of elliptical galaxies, which lack star formation, in the past and in the present day. These dead galaxies have used up all their fuel. Thus, any increase in their black hole mass over this time is not due to the normal processes by which black holes grow by accumulating matter. The team considered that these black holes actually contain vacuum energy and that they are “coupled” to the expansion of the universe, so that they increase in mass as the universe expands. The idea that black holes might contain vacuum energy (a manifestation of dark energy) is not particularly new, but this latest model assumes that this energy (and therefore the mass of the black holes) would increase with time as the universe expands as a result of cosmological coupling. The team calculated how much of the dark energy in the universe they could attribute to this process. They found that black holes could potentially explain the total amount of dark energy we measure in the universe today. It is considered that this theoretical result could solve one of the most fundamental problems in modern cosmology and provides a possible origin for the dark energy in the Universe.28
-In connection with the problem of the the dark energy’s provenience, a new survey of more than 200 of supermassive black holes found that the emitted jets are much more powerful than scientists thought. Astronomers don't know what powers these jets, but they proposed the conclusion that the jets are tapping into the rotational energy of the black hole itself.29 Also, it is known that the stars which are called "blue fast optical transients" (LFBOT) are much brighter than the supernovae. They light up very quickly and are extremely hot, reaching temperatures of up to nearly 40,000 degrees Celsius, and emit blue light. Supernovae normally flare up and then die out over weeks or months, but the LFBOTs flare up in just three or four days and turn off in a much shorter time period.30
-The recent observation that black holes in certain Einstein-Maxwell-dilaton (EMD) theories can violate the entropy super-additivity led to the suggestion that these black holes might repel each other without electrostatic force between them, the dilaton being the antigravity agent, (i.e. two black holes might not always attract).31 It was also shown that the potential of dilaton field can be taken in an exponential form and that the dilaton can be a candidate for dark energy that can explain the accelerated universe, an analytical solution of Einstein equation being found.32 These results led one to propose that and the dilaton may play the role of antigravity.33
-In CGT3 the electronic neutrino results as couple of two super-heavy centroids of electrons with opposed e-charge, and it was deduced that sinergonic winds (of heavy etherons) are generated in the gammon
electronic neutrino conversion:
(28)
–when also the sinergonic vortices of the paired electrons are reciprocally annihilated. These sinergonic winds contribute to the mean value
of the dark energy” as fluxes of quanta of an antigravitic (pseudo)charge of the “black hole”.
Writing the electric field energy of an electron in the form:
for:
and
it results for the electron’s (electro) gravitic energy, that:
(29)
i.e.- the gravitic field energy of the me-gravitic charge is of ~1042 times smaller than the etheronic energy contained by the sinergonic - vortex of the electron’s magnetic moment:
.
In consequence, according to the CGT’s electron model, (which deduces a value
also for the sinergonic energy contained by the volume of Compton radius:
),3 the releasing of the sinergonic energy of the destroyed degenerate electrons of the nucleons’ quarks (considered as in CGT, as non-destructively collapsed Bose-Einstein condensate of ‘gammons’), in the process of matter ®energy conversion at the surface of a black hole or inside its volume, could explain the amount and the provenience of the dark energy in the actual Universe, responsible for the Universe’s expansion, in concordance with the mentioned conclusions looking the phenomenon called ‚cosmological coupling’.
Because the radial releasing of the sinergons of destroyed
– vortices generate periodically an antigravitic (pseudo)charge Ma = kam, (m- the mass of the destroyed particle, ka >>1), in condition of the existence of a magnetically ‘arrested’ disk of matter around the gravistar’s hard core (HC), (MAD - which contributes also to the black hole’s growing), it results that the CGT’s model of gravistar could explain not only the source of the dark energy, but also the repulsive property of some black holes in condition of the existence of a ‘dilaton’ field- considered by the EMD theories. But because in the considered gravistar’s case, this repulsive field of the central HC of black hole type can be produced only pulsatory, it raises also the question if a pulsatory gravistar can produce a removal total mechanical work LT over a material particle or celestial body mt on a given distance
.
- In CGT, the force generated by gravistar’s HC as in the Fatio-LeSage’s theory, has the expression:
Fg = mtkhPg = GmtMC/r2, (
–the equivalent pressure generated by the un-compensated radial flux of (gravitonic) etherons with impulse density
;
).
Let us suppose that at the surface of the gravistar’s HC of radius R0, in a cubic meter is destroyed simultaneously a quantity of nucleons:
, which –according to CGT,3 will generate a radial flux of sinergons of energy density:
corresponding to an impulse density:
and to a static pressure
, which will generate –over each quanton mh of a test particle mt, (particularly –a photon), a force of Stokes type, generating a total antigravitic force:
(30)
(MA- the antigravitic charge generated by a matter quantity
simultaneously destroyed at the HC’s surface ; kA –proportionality constant, depending on the kinematic viscosity ne of the flux of heavy etherons and on the quanton’s radius, rh ; kh = 27.4).3
The exponential factor f(r) is justified by the gravitational attraction over the sinergons, in the next way: Supposing an initial speed
for the released sinergons at matter-energy conversion, after a radial distance: r characterized by a (quasi)constant gravitational acceleration aC, the sinergons’ speed will be given by the classic formula:
.
By the formula:
, admitting the approximation: 1 + x » ex, for the previous case,
, it results that:
(31)
-If the gravistaric HC has also a magnetization MB that generates a magnetic B-field of the form:
, with
, the sinergonic (pseudo)vortex of this magnetic potential A will generate –according to CGT, a magneto-gravitic potential
and a magneto-gravitic force:
, which can be estimated by applying the Bernoulli’s law to the etheronic medium existent around the gravistaric HC, (composed of light and heavy etherons):
constant, resulting that:
(32)
The dynamic sinergonic pressure Pds(r) = ½rsvw2 can estimated by Eq.(21a) of CGT:
, (33)
,
for a variation of B(r) of the form:
, resulting that:
(34)
resulting that:
.(34')
By
[m2/C] and taking for
the value obtained in CGT for the inertial mass of the vecton (vector photon of ~ 3K-radiation and of electric field, of mass
):
,16 it results that:
Considering that the gravistaric HC is a charged rotational black hole of 25 MS (MS –solar mass:
) and radius
, that has also a magnetaric B-field of
1011 T –at its surface, it results that:
In the same time, the Newtonian force/kg will be:
It results- in consequence, that even if HC is magnetaric, the gravitomagnetic force is neglijible compared to the Newtonian gravitic force generated by a relative small stellar black hole, and can be neglected. So, the HC must be a black hole in a purely gravitational sense, for retain also relativist particles and pseudo-scalar photons. However, the magneto-gravitiv force Fgm of Magnus type, generated by the sinergonic vortex
corresponding to the sinergonic energy of the magnetic A-potential of the HC’s B-field, remains of values that maintain quantons and vector photons and electrons around the gravistar’s HC.
-For r < Rl, by considering a short time
of existence of the antigravitic (pseudo)charge
MA >> MC , it is understood that the particles mt of the magnetically ‘arrested’ accretion disk (MAD) will be rejected with a force Fa(r) that will produce a mechanic work:
(admitting the conclusion that the test particle mt obtains a relativist speed in the time
).
The obtained kinetic energy
will be lost by the test particle on a distance
as consequence of the mechanic work LG produced mainly by the gravitation force: Fg(r) (and by Fgm(r) << Fg(r)), i.e.:
, (35)
(
).
It results that:
(36)
So, inside the volume of radius
,
, if the t- period between the antigravitic (short) pulses
satisfy the condition:
, the MAD will be gradually destroyed at the HC’s surface, (with a period
between the moments
of MA –antigravitic (pseudo)charge’ generating), with the releasing of mixed radiation (including X-rays, gamma radiation and electronic neutrinos). But because in the polar zones the radial speed of these emitted jets are less affected (diminished) by the dynamic pressure
of the etherono-quantonic vortex
of the HC’s magnetic field, the fact that the spinning surface of the gravistar’s HC can emit relativist jets of particles and photonic radiation, as it vas astrophysically observed, excepting the released sinergons, which are slowed by the gravitational Fg –force but not retained by the HC’s gravitic field, (Fgm not acting on sinergons, on their volume, because it is generated by sinergons with approximately the same volume).
-For r > Rl, an external body gravitationally attracted by HC can be repelled by the periodically generated MA –antigravitic charge, up to a distance RR > Rl, given by the equality:
.
For
, because:
, it results that:
(37)
For r >> Rl, it results that: (1/R0-1/r) » 1/R0, and to a distance
, we have:
(38)
(by considering vs as quasi-constant on distances comparable with the diameter of mt -test-particle).
From Eq. (37) it results that:
, and with
, Eq.(38)
becomes:
(39)
that- because the antigravitic field generated by the antigravitic charge GA vary approximately with:
, conform to Eq. (38), (because the spherical distribution of the released sinergons and the gravitationally reducing of their speed), to distances R > Rl , will give:
(40)
and:
(41)
Because the sinergonic pulses of duration dt generates gravitational waves, for R>> R0 we must have- by Eq. (31):
, i.e.:
, i.e. it can be black hole in purely gravitational sense, for rs > R0 > 0.7276 rs .
For R0 a little lower than rs = 2GMC/c2, (the HC’s Schwarzschild radius), said:
, we will have: vs(R) = 1.07c . Writing:
, Eq.(41) may be written as:
(42)
Some particular values of MC and R0 can be relevant:
a1)-Taking in Eq. (37)
, (super-massive black hole), we obtain for Rl the value:
.
From Eq. (37) it results that
, so the test particle loses its kinetic energy in a time:
If the test particle is a nucleus from the MAD, it results that
.
a2)- Taking in Eq. (37)
, (super-massive b. h.), we obtain for Rl the value:
.
From Eq. (37) it results that
, so the test particle loses its kinetic energy in a time:
.
If the test particle is a nucleus from the MAD, it results that
.
The sinergons of the antigravitic pulses, released with
, will have at the limit Rl a kinetic energy:
,
(
) (43)
and the antigravitic pulses can be detected as gravitational waves.
The energy lost by sinergon at
will be:
;
(For obtain
would be necessary to have:
.
-b)-For r > Rl, by taking
in the previous case, a2):
by Eq. (42) it results:
Eq. (40) gives:
The same conclusion
is obtained also for the case a1), by taking RL = 2Rl.
- Extrapolating, we can conclude that the sinergons released by the destruction (by matter→energy conversion) of the MAD cannot generate an expansion of the matter existing over the limit Rl, but the generated antigravitic (pseudo)charge can interrupt periodically the matter’s ‚eating ‚by the black hole. An argument for this conclusion can be also the fact that a team of astrophysicists observed tidal disruption events to a white dwarf named Swift J0230 observed in X-rays spectrum, with a mass of three times the Eart’s mass, each time when it passes close to the black hole existent in the center of the galaxy named 2MASX J02301709+2836050, a small one with a mass of about 10,000 to 100,000 times the sun’s mass. Regular observations of Swift J0230 revealed a rapid drop in the star's brightness on the fourth day. According to the new study, that's the point at which it dimmed by a factor of 20 in just 57 kiloseconds (15.8 hours). Shortly after, the star became elusive to telescope observations. But why this black hole only partially disrupts the star is not very well understood.34
However, the HC’s antigravitic charge MA can be generated also by matter→energy conversion inside the gravistaric HC, if we consider a HC’s shell of cold current strange quarks forming a crystalline network, (as in the model of the known quark star made entirely of quark matter, which would be stable if they quickly transform into strange quark matter),35 or even of nucleons in quasi-crystalline state (depending on the HCi’s mass), taking into account the fact that the high density of the quak matter and the strong force nucleons ensures – at T→0K, a high inter-quarks force and binding energy, (at least tens of MeV/current quark), which can determine the resistance of the HC’s surface at high internal pressure Pi , and the fact that the sinergons released by the destroyed matter and radially emitted can penetrate the HC’s shell of strange quarks matter.
The possible cause of the interior destruction of nucleons inside the gravistaric HC is not only the pressure given by the gravitational attraction of its inner part , but also a small difference between the angular rotation speed w of this inner part HCi-supposed to be of gravitic black hole type (network of current quarks considered in CGT’s model) and its rotated shell, HCe , formed by strange current quarks, (in conformity with Ref. 35). This angular rotation speed difference
(Figure 1) will generate a neutronic liquid shell F, when
increases and decreases periodically changing its sign, as a consequence of HCe’s growth, similar to the case of the Earth’s convective liquid inner shell (of ionized atoms) which- in Bullard’s self-exciting dynamo model36 explains the generating of Earth’s magnetic field.
Inside this neutronic liquid shell, matter→energy conversion can be generated due the high radial pressure gravitationally generated by the attraction of the inner part Hci, conform to the model. -If the antigravitic (pseudo)charge
of the inner part HCi cannot destroy the solid shell HCe, but is enough high for cancel the gravitational attraction of HCi and for generate matter’s expansion, it is able to generate a mechanic work higher than that of the gravitational force:
, if its duration
is enoug high and its generating period is
.
The generated antigravitic field, can be- in this case, a natural equivalent of the dilaton field of the EMD theories.
The internal pression must satisfy the equation:
(44)
with:
-the superficial tension of HCe; Fq –the strong force between two current strange quarks at
fm (the approximate diameter’s value of a preonic current quark; Rs –the inner radius of HCe –shell) or between two cold nucleons at ~ 1 fm inter-distance, (depending on the HCi’s mass).
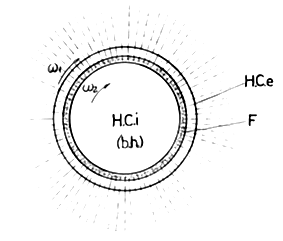
Figure 1 Antigravitic (pseudo)charge generating by matter→energy conversion inside the gravistar’s HC.


