The paper brings supplementary arguments regarding the possibility of cold particles forming as collapsed cold clusters of gammons–considered as pairs:${\gamma }^{*}=\left(e^{-}{e}^{+}\right)$ of axially coupled electrons with opposed charges. It is argued physico–mathematically that the particles cold forming from chiral quantum vacuum fluctuations is possible at$T\to 0K$ , either by a vortexial, magnetic–like field or by already formed gammons, in a “step–by–step” process, by two possible mechanisms: a)–by clusterizing, with the forming of preons$z^0=34m_e$ , and of basic bosons:$z_p=7z^0;z_2=4z^0$ , with hexagonal symmetry and thereafter–of cold quarks and pseudo–quarks, by a mechanism with a first step of $z^{*}/{\left(q^{\pm }/q^0\right)}^{*}$ –pre–cluster forming by magnetic interaction and a second step of $z/\left(q^{\pm }/q^0\right)$ –collapsed cluster forming , with the aid of magnetic confinement, and b)–by pearlitizing, by the transforming of a bigger Bose–Einstein condensate into smaller gammonic pre–clusters which may become particle–like collapsed BEC.

Keywords: cold genesis, bose–einstein condensate, quasi–crystal quark, dark energy, quantum vortex

In a previous paper¹ were presented briefly some basic particle models resulted from a cold genesis theory of matter and fields^2–5 of the author, (CGT), regarding the cold forming process of cosmic elementary particles, formed–according to the theory, as collapsed cold clusters of gammons–considered as pairs:${\gamma }^{*}=\left(e^{-}{e}^{+}\right)$ of axially coupled electrons with opposed charges, which gives a preonic, quasi–crystalline internal structure of cold formed quarks with hexagonal symmetry,⁵ based on $z^0\approx 34m_e$ preon–experimentally evidenced in Krasznahorkay et al.,⁶ but considered as X–boson of a fifth force, of leptons–to quark binding, and on two cold formed bosonic ‘zerons’ :$z_2=4z^0=136m_e$ ; and $z_{\pi }=7z^0 =238m_e$ , formed as clusters of degenerate electrons with degenerate mass and magnetic moment and with degenerate charge$e^{*}=\left(\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\right)e$ , (characteristic to the up–quark–in the quantum mechanics).

According to this theory,^2–5 based on the Galilean relativity, the magnetic field is generated by an etherono–quantonic vortex${\Gamma }_M={\Gamma }_A+{\Gamma }_{\mu }$ of s–etherons (sinergons–with mass$m_s\approx {10}^{-60}kg$ ) giving the magnetic potential A by an impulse density:$p_s\left(r\right)={({\rho }_s\cdot c)}_{r }$ and of quantons (h–quanta, with mass:$m_h=h\cdot 1/c^2\approx 7.37x{10}^{-51}kg$ , formed as compact cluster of sinergons) giving the magnetic moment and the magnetic induction B by an impulse density:$p_c\left(r\right)={({\rho }_c{v}_c)}_r$ , the nuclear field resulting from the attraction of the quantum impenetrable volume u_i of a nucleon in the total field generated according to fields superposition principle, by the Nsup>n

$V_n\left(r\right)={\upsilon }_i{P}_n=V_n^0\cdot e^{-r/}{}^{\eta *}; P_n\left(r\right)=\left({}^1{/}_2\right){\rho }_n\left(r\right)\cdot c^2$ (1)

By an electron model with radius: a = 1.41fm and with exponential variation of the quantum volume density and of the magnetic field quanta: ${\rho }_{\mu }\left(r\right)\approx {\rho }_e\left(r\right)={\rho }_e{}^0·e^{-r/}{}^{\eta }$ ;$\eta \approx 0.96fm$ ;${\rho }_e{}^0=2.22x{10}^{14}kg/m^3$ .

In the base of some neo–classic (pre–quantum) relations of the electric and magnetic fields:^2–5

$\begin{array}{l}{{\displaystyle E}}_s(r)={{\displaystyle k}}_1\cdot {\rho }_e(r)\cdot {\text{v}}_{\text{c}}^{\text{2}}=\frac{\text{1}}{\text{2}}{{\displaystyle k}}_1\cdot \frac{\Delta p_c^2}{\Delta t};{\text{ q}}_{\text{s}}=\frac{\text{4}\pi \cdot {\text{r}}_{\text{q}}^{\text{2}}}{{\text{k}}_{\text{1}}};\\ \text{B }={\text{k}}_{\text{1}}\cdot {\rho }_{\mu }(r)\cdot {\text{v}}_{\text{c}}\text{; (}{k}_1=\frac{4\pi \cdot a^2}{e}=1.56x{10}^{-10}\frac{m^2}{C};{\text{ v}}_{\text{c}}\approx c)\end{array}$  (2)

In two relative recent papers,^7,8 were brought arguments for two possible mechanism of cold particles forming as collapsed Bose–Einstein condensate (BEC) without destruction:
a) by clusterizing and cold collapsing without destruction, from a gammonic quasi–crystallin pre–cluster N^z,7 or

b) by pearlitizing, by the fragmenting of a bigger BEC.⁸ The particles cold forming by clusterizing may results–according to CGT, in a “step–by–step” process,⁷ supposing:
a1)$z^{0*}/z^0$ pre–cluster/cluster forming, with the aid of magnetic confinement, with a metastable equilibrium interdistance between gammons with antiparallel magnetic moments:$d_e=a=1.41fm$ (Figure 1);

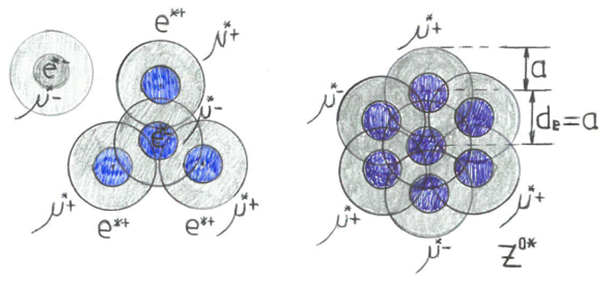
Figure 1 The z⁰*–pre–cluster forming.

a2)$z_2{}^{*}/z_2$ and $z_{\pi }{}^{*}/z_{\pi }$  are pre–cluster/cluster forming;
a3) $(q^{\pm }/q^0)$ –quark or neutral pseudo–quark pre–cluster/cluster forming;
a4) pre–cluster of quarks or pseudo–quarks forming;
a5) elementary particle/dark boson forming, or directly:
a1’) quark pre–cluster forming (Figure 2) (Figure 3)®collapsed quark cluster forming;

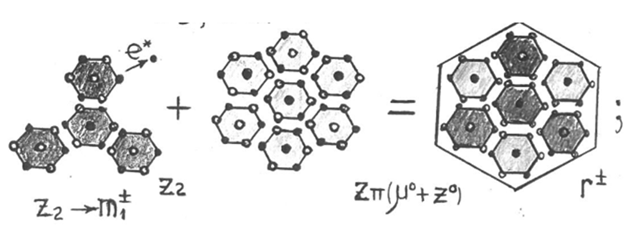
Figure 2 The m₁–and r*–quark pre–cluster forming.

Figure 3 The cold forming of baryonic quarks.

a2’) elementary particle/dark boson forming (cluster of quarks with the current mass in the same baryonic impenetrable quantum volume, u_I–Table 1).

The particles cold forming by pearlitizing supposes:
b1) the forming of a bigger BEC of gammons, with the concentration of particles:$N_0\approx 1/a^3=3.57x{10}^{44}$ , (a=1.41 fm), in a strong gravitational or magnetic field:$B_{\gamma }=(2.2x{10}^6÷8.3x{10}^7)T$ , at temperatures $T=T_p=(4.8x{10}^{-11}÷1.8x{10}^{-10})K<T_B$ , i.e.–Much lower than the transition temperature $T_B$ –corresponding to a very low (neglijible) fraction N₀/N; (N($T_B$ )–the initial concentration of particles, (for example, for$N\approx {10}^{24}$ , T_BE(B=0)=1464K), the length along the$B_{\gamma }$ –field, of a gammonic BEC with the concentration N₀ formed at T=T_p resulting of value: $L\approx 2.5x{10}^{-7}m$ ;⁸
b2) The pearlitizing of the resulted BEC by large temperature oscillation around the transition value$T_B$ . The necessity of temperature oscillation around the transition value$T_B$ for the BEC’s pearlitization results as consequence of the residual (reciprocal) magnetic interactions between gammons, which gives a superficial tension$\sigma$ .

For example, considering a radius r_p of meta–stable equilibrium of a drop of BEC formed by the BEC’s pearlitization and maintained by the equilibrium between the force generated by the internal vibration (thermal) energy$F_t\left(r_p\right)=V\cdot N_0{k}_B{T}_i$ and the force generated by the surface tension $\sigma$ :

$\frac{dE}{dr}=-P_0\frac{dV}{dr}+\sigma \frac{dS}{dr}=0\text{ ; V}=\frac{\text{4}\pi }{\text{3}}{r}^3\text{ ; S}=\text{4}\pi \cdot {\text{r}}^{\text{2}};$ (3)

Because$\sigma =\left(\mathrm{½}\right)F_{\lambda }/1$ , (the force rectangular on unit length), for:$N_0\approx 1/a^3=3.57x{10}^{44}$ , (a=1.41fm–the metastable equilibrium inter–distance between gammons),⁸ the equilibrium radius is:
$r_p=\frac{2\sigma }{P_0}=\frac{F}{l\cdot P_0}\approx \frac{F_{\gamma }}{l_{\gamma }\cdot P_0}\approx \frac{{\mu }_0}{2\pi }\frac{{\mu }_{\gamma }^2}{d_e^3\cdot l_{\gamma }}{\frac{\text{1}}{{\text{N}}_{\text{0}}{k}_{B}T}}_{\text{i}}[m]$  (4)

In which de is the inter–distance between adjacent gammons and$l_{\gamma }$ is the length of a gammon. It is necessary in consequence–for estimate the value r_p, to estimate the value of gammon’s length and magnetic moment${\mu }_{\gamma }$ .

It was argued in CGT,⁷ that is not logical to consider at an inter–distance$d_i<r_{\lambda }=h/2\pi m_{e}c=386fm$ , a value of the electron’s magnetic moment radius:$r_{\mu }$ , higher than the inter–distance $d_i$ , resulting a value:$r_p\approx 5.5x{10}^{-9}m$ for$T_B\approx {10}^{3}K$ with$r_p~1/T_i$ , by the use of equation (2) and with$r_{\mu }\approx d_i$ .⁸

If we use the expression (2) of the B–field, because the magnetic moment radius $r_{\mu }$ , represents in the etheronic, quantum–vortexial model of magnetic moment, the radius until which the B–field quanta have the light speed c, and because–for$d_i<r_{\lambda }$ , for$\left(e^{-}-e^{+}\right)$ interaction is maintained the relation:B = E/c, we may re–write this relation in the form:

$B(d)\approx \frac{\text{E(d)}}{\text{c}}=\frac{e}{4\pi {\epsilon }_0{d}^{2}c}=\frac{{\mu }_0}{2\pi }\frac{e\cdot r_{\mu }c}{2\cdot d^3},\text{ a}<\text{d}<{\text{r}}_{\lambda }\text{ ; }\Rightarrow {\text{r}}_{\mu }\approx d$  (5)

Resulting in consequence, the expression of the electron’s magnetic moment at inter–distances$d_i\le r_{\lambda }$ . The reciprocal equilibrium position of gammonic electrons, in the particular case of a semi–hard gamma quantum considered–in CGT, as gammonic pair:${\gamma }^{*}=\left(e^{-}{e}^{+}\right)$ , may be estimated by equation (5), imposing a correspondence with the conclusion of quantum mechanics regarding the ($e^{-}{e}^{+}$ ) pair production, which indicates as minimal energy value of an external electric or magnetic field which may convert the gamma quantum into stable electrons, the value:$E_{\gamma }=2m_e{c}^2$ . In CGT, based on the classical mechanics and relativity, this value $E_{\gamma }$ has the sense of the energy necessary to ‘split’ the gamma quantum into the component electrons with opposed charges:

$E_{\gamma }=2m_e{c}^2=\frac{e^2}{4\pi {\epsilon }_{0}a}=\frac{{\text{e}}^{\text{*2}}}{4\pi {\epsilon }_0{d}_e}+B_e\cdot {\mu }_e(d_e)=\frac{e^{*2}}{4\pi {\epsilon }_0{d}_e}+\frac{{\text{e}}^{\text{*2}}}{8\pi {\epsilon }_0{d}_e}$  (6)

In which we considered a possible degenerate charge,$e^{*}\le e$ . This interpretation is logical by the fact that the nuclear E–field may split the$\gamma$ –quantum only if it can act over internal e(e*)–charges of opposed sign.

Between e and (2/3)e, considering an electric permittivity$\epsilon ={\epsilon }_0{\epsilon }_r\approx {\epsilon }_0$ , we have the next significant possibilities:

1.  $e^{*}=e,\Rightarrow d_e=1.5a$ ;
2. $d_e\approx a,\Rightarrow e^{*}\approx \sqrt{\left({}^2{/}_3\right)e}$ ;
3. $e^{*}\approx \left({}^2{/}_3\right)e,\Rightarrow d_e\approx \left({}^2{/}_3\right)a$ .

Because for a photon–like gammon its length must exceed its diameter proportional with the speed,⁹ it results that the case a) corresponds to a relativist gammon ($v\to c$ ), which–in CGT, may have simultaneously rest mass and the c–speed, and the case c) correspond to a linked gammon, which is confined inside a bigger elementary particle (mesonic or baryonic), the degenerate charge$e^{*}\approx \left({}^2{/}_3\right)e$ being specific to the up–quark , (p–quark–in CGT).^2–5 So the case b) corresponds to a gammonic pre–cluster, in accordance also with the quantum mechanics.

The degenerate charge’s radius:$r_e(e^{*}=\sqrt{\left({}^2{/}_3\right)}e)$  for $d_e\approx a$  , results from (6), according to a CGT’s relation:

$e^{*}(a)=\frac{2S_x^e}{k_1}\approx \frac{4\pi \cdot r_e^2}{k_1}=e{\left(\frac{r_e}{a}\right)}^2\approx e{\left(\frac{r_e}{d_i}\right)}^2=\sqrt{\frac{2}{3}}e;\Rightarrow r_e\approx \text{0}{\text{.9d}}_{\text{i}}{\text{; S}}_{\text{x}}=\pi {{\text{(r}}_{\text{e}}+{\text{r}}_{\text{v}}\text{)}}^{\text{2}}\text{;}$ (7)

but in the hypothesis:$\epsilon ={\epsilon }_0{\epsilon }_r\approx {\epsilon }_0$ . However, the so–called “stopped light experiment”^10,11 showed that a Bose–Einstein condensate determine a high slowing of the light passed through it, at a value$v_c<<c$ , so for$d_e\approx a$ , by the known relation:$n=c/v_c\approx \sqrt{\epsilon }$  it results that we may consider the approximation:$\epsilon ={\epsilon }_0{\epsilon }_r\approx {\epsilon }_0$ only in the case:d_e=1.5a, corresponding to a relativist gammon, for the case b) and c) resulting that${\epsilon }_r>1$ , so–the charge degeneration may be less accentuate,$(e^{*}\left(a\right)>\sqrt{\left({}^2{/}_3\right)}e)$ , because the decreasing of the V_e–potential with$\epsilon$ . By the proportionality between n,$\epsilon$ and the quanta density, deduced in CGT: n,$\epsilon ~{\rho }_c$ ,⁹ because the proportionality:${\rho }_c~r^{-2}$ for r > a, it results that:

${\rho }_c~r^{-2},\left(r>a\right)\Rightarrow \epsilon \left(a\right)/\epsilon \left(d_e\right)\approx {\left(d_e/a\right)}^2=2.2$ (8)

As consequence, the relation (6) must be re–written in the approximate form:

$E_{\gamma }=2m_e{c}^2=\frac{e^2}{4\pi {\epsilon }_{0}a}=\frac{{\text{e}}^{\text{*2}}}{4\pi {\epsilon }_0{d}_i}+B_e\cdot {\mu }_e(d_i)=\frac{e^2}{4\pi {\epsilon }_0{\epsilon }_r{d}_i}+\frac{{\text{e}}^{\text{2}}}{8\pi {\epsilon }_0{d}_i}$  (9)

with${\epsilon }_r=\epsilon \left(a\right)/\epsilon \left(d_e\right)\approx 2$ , resulting that:$V_e\left(a\right)\approx V_{\mu }\left(a\right)$ . This result explains also the possibility of particles forming by clusterizing, by the conclusion that–in a section plane of a preonic $z^{0*}$ –pre–cluster formed with hexagonal symmetry, the inter–distance of metastable equilibrium d_i =a results by the equality$V_e\left(a\right)\approx V_{\mu }\left(a\right)$ for the interaction with the central electron, either by electrostatic attraction and magnetic repelling or by magnetic attraction and electrostatic repelling (Figure 1) (Figure 4), the gammonic pre–cluster’s collapsing resulting by the attraction between adjacent circularly disposed gammonic electrons, the central chain of axially coupled gammons giving the z⁰–preon magnetic moment, which explains similarly the cold confining of a pre–cluster of z⁰–preons, and so on (Figure 5).

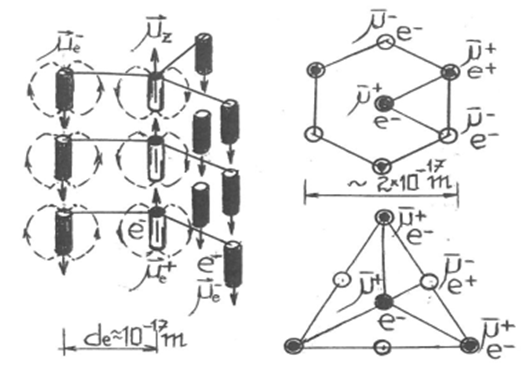
Figure 4 The forming of the z⁰–cluster’s kernel.

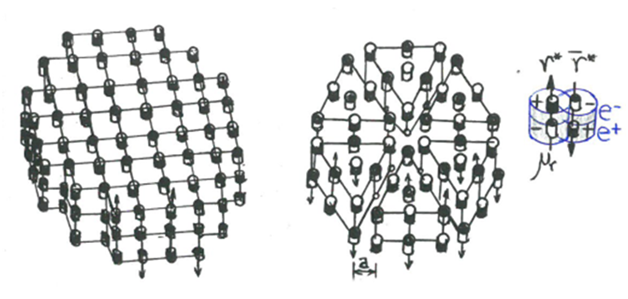
Figure 5 Parts of crystallized gammonic pre–cluster which may result by a BEC’s pearlitizing.⁸

The total collapse of the gammon is impeded–according to CGT, by a repulsive field and force with exponential variation, generated by the ‘zeroth’ vibrations of the electron’s kernel (centroid) and acting over a quantum volume of the electron: u_e(r_e » d) with a force:$F_r\left(d\right)\approx 2S_x{\rho }_r\left(d\right)c^2$ , (which explains also the non–annihilation between e^–and e⁺ at low energies), deduced considering a quasi–elastic interaction of field quanta with the interaction surface$S_x=\pi d^2$ of the repelled electron.

We may consider–in consequence, that the gammonic electrons have a remnant vibration of spin and of translation between the interdistances: d_e=1.5a and d_i’=(2/3)a , as consequence of the self–resonance induced by the repulsive potential V_r(d), the value d_e=a being a mean value, the equilibration between the attraction force F_a(d), of magnetic and electric type, and the repulsive force$F_r\left(d\right)=-\nabla V_r\left(d\right)$ , being realized at d £ di’ = (2/3)a, the action of magnetic potential$V_{\mu }$  being diminished by V_r with a factor f_d £1.

For the approximation of the superficial tension$s_{\gamma }=F_{\gamma }/2l_{\gamma }$ , according to the previous considerations, we may approximate that–at the gammonic pre–cluster’s surface with a mean interdistance d_e=a between adjacent gammons, the binding force$F_{\gamma }\left(a\right)$ is given by the magnetic interaction between gammons, the electric interaction force between gammons (of inter–dipoles type) being considered compensated by the repulsive force F_r (d), in a simplified model.

At increased temperatures$T_i\ge T_B$ , the linking (magnetic) energy resulted from equation (9):$V_{\mu }\left(a\right)\approx m_e{c}^2$ , is diminished by the vibration energy according to a relation of the total binding energy of the form:$V_T\left(a\right)=f_d·V_{\mu }\left(a\right)–k_B{T}_i$ , ($f_d~T_i$ –diminishing factor), the binding force being in this case:

$F_T(a)={\text{F}}_{\mu }(a)\left(1-\frac{T_{\text{i}}}{T_C}\right)\approx {\text{f}}_{\text{d}}\frac{m_e{c}^2}{a}\left(1-\frac{T_i}{T_C}\right){\text{; T}}_{\text{C}}={\text{f}}_{\text{d}}\frac{m_e{c}^2}{k_B}$  (10)

In consequence, we may approximate the expression of the superficial tension${\sigma }_{\gamma }=F_{\gamma }/2l_{\gamma }$ as being given by the magnetic interaction force between two adjacent gammonic electrons, according to the approximation relation:

${\sigma }_{\gamma }=\frac{{\text{F}}_{\gamma }}{\text{2}\cdot \text{l}}\approx \frac{F_{\mu }^e}{2a}={\text{f}}_{\text{d}}\frac{m_e{c}^2}{2a^2}\left(1-\frac{T_i}{T_C}\right){\text{; T}}_{\text{C}}={\text{f}}_{\text{d}}\frac{m_e{c}^2}{k_B}=f_d\cdot \text{5}{\text{.9x10}}^{\text{9}}\text{ K}$  (11)

with$f_{d }\approx (1-F_r\left(a\right)/F_{\mu }\left(a\right))\le 1$ . The equilibrium radius r_p of the pearlitic gammonic pre–cluster results in this case according to the approximate relation:

$r_p=\frac{2{\sigma }_{\gamma }}{P_0}=f_d\frac{m_e{c}^2}{k_B}\frac{a}{T_i}\left(1-\frac{T_i}{T_C}\right)\approx \frac{T_C}{T_i}\text{a}\approx f_d\frac{\text{8}{\text{.3x10}}^{-6}}{{\text{T}}_{\text{i}}}[m]$  (12)

For$T_i=T_B\approx {10}^{3}K$ and$f_d\approx 1$ , it results:$r_p\approx 8x{10}^{-9}m$ . When$T_i>T_B\left(r_p\right)$ , the (metastable) equilibrium radius results smaller, according to (12), (r_p’< r_p), but because the equilibrium inter–distance cannot decrease when the internal energy kBTi increases, according to equation (4), it results that the equilibrium radius of the BEC may be re–obtained at the specific decreased value only by the decreasing of the particles number of the BEC, so the pearlitization with the forming of quasi–cylindrical pre–clusters of baryonic neutral particles corresponding to a radius:$r_b<r_a$  may be formed by large oscillations of the internal temperature T_i–given by the boson’s vibrations, around the value$T_i{}^{*}=T_B$ .

On the radial direction, for a pre–cluster with the radius r_c< r_p , the electric interaction between gammons having the electron’s charge in surface, may be neglected for d_i< a and we may consider that the magnetic potential$V_{\mu }$ between gammons is partially equilibrated by the vibration energy k_BT_i and by the repulsive potential Vr(d) acting over a quantum volume of the electron:${\upsilon }_e^e(r_e\le d)$ .⁷

For conformity with the general electrogravitic form of CGT,^2–4 we will take for the repulsive force F_r(d), the form correspondent with equation (2):

$F_r(d)=-\nabla V_r\text{'}=q_s\cdot E_s=S_x\cdot 2{\rho }_r^0{c}^2\cdot e^{-\frac{d_i}{{\eta }_r}};{\text{ S}}_{\text{x}}=\pi {\text{ r}}_{\text{c}}^{\text{2}}{\text{; r}}_{\text{e}}\le d_i$ (13)

i.e.–considering an exponential variation of the quanta density and a quasi–elastic interaction of V_r–field quanta (approximated with small radius–in report with the radius r_c of the static q_s–charge) with the interaction surface:

$S_x\left(r_c+r_h\right)\approx S_x\left(r_c\right)=\pi r_c{}^2\approx \mathrm{½}{S}_x{}^{*}\left(e^{*}\right).$ (14)

Considering the effective action of the V_r–field quanta over the qs–pseudo–charge in a quasi–constant solid angle Α_s,rc may be approximated as given by the result of equations (6)+(7):$r_c\approx d_i$ , which may be used also for approximate the value of the reciprocal magnetic moment :${\mu }_r=\mathrm{½}{e}^{*}c\cdot d_i$ .

Because the magnetic force results from the gradient of quanta density${\rho }_{\mu }\left(d\right)$ which gives by equation (2), the magnetic induction B(d), we must deduce the magnetic force considering that the magnetic moment${\mu }_r$ of the attracted electron is quasi–constant to a short derivation interval$\delta d_i$ , retrieving the expression of the magnetic force between two degenerate electrons in the form:⁷

$\begin{array}{l}{F}_{\mu }={\mu }_r(d_i)x\nabla B_e(a)\cdot e^{\frac{a-d_i}{\eta }}\cdot \left(1-\frac{T_i}{T_C}\right)\approx -f_{\mu }\frac{{\text{e}}^{\text{2}}{d}_i^2}{8\pi {\epsilon }_0{a}^4}\left(\frac{{\text{d}}_{\text{i}}}{\eta }\right)\cdot {\text{e}}^{\frac{{\text{a-d}}_{\text{i}}}{\eta }}\text{;}\\ {\mu }_{\text{r}}=\frac{{\text{e}}^{\text{*}}c\cdot d_i}{2}=\frac{{\text{ecd}}_{\text{i}}^{\text{3}}}{{\text{2a}}^{\text{2}}}{\text{; e}}^{\text{*}}=\frac{4\pi r_e^2}{k_1}\approx {\left(\frac{d_i}{a}\right)}^{2}e\text{; }\eta \approx \text{0}\text{.96fm}\end{array}$ (15)

which results from the exponential variation of the B–field quanta density inside the electron’s quantum volume,$f_{\mu }~T_i$  being a diminishing factor resulted by the periodically partial destroying of the internal etherono–quantonic vortex${\Gamma }_{\mu }$ of the magnetic moment by the vibration energy:${\epsilon }_v\approx k_B{T}_i$ . By (15) the equality:$F_r\left(d_i\right)=F_{\mu }\left(d_i\right)$ , for$T_i<<T_C$ , gives:

$\begin{array}{l}{F}_{\mu }\approx {\text{f}}_{\mu }\frac{{\text{e}}^{\text{2}}{d}_i^2}{8\pi {\epsilon }_0{a}^4}\left(\frac{{\text{d}}_{\text{i}}}{\eta }\right)\cdot {\text{e}}^{\frac{{\text{a-d}}_{\text{i}}}{\eta }}=2S_x{\rho }_r(d_i)c^2\approx \text{ 2}\pi {\text{d}}_{\text{i}}^{\text{2}}\cdot {\rho }_r(d_i)c^2\text{;}\\ \Rightarrow {\rho }_r(d_i)={\rho }_r^0(T_i)\cdot e^{-\frac{d_i}{{\eta }_r}}=f_{\mu }{\rho }_e(a)\left(\frac{{\text{d}}_{\text{i}}}{\eta }\right)\cdot {\text{e}}^{\frac{{\text{a-d}}_{\text{i}}}{\eta }}\text{; }{\rho }_{\text{e}}(a)=\frac{{\mu }_0}{k_1^2};{\text{ f}}_{\mu }\le 1\end{array}$ (16)

with${\rho }_e\left(a\right)={\mu }_0/k_1{}^2=5.17x{10}^{13}kg/m^3$ 1 and with:${\rho }_r{}^0\left(T_i\right)=f_{\mu }(d_i/\eta ){\rho }_e{}^0; {\rho }_e{}^0={\rho }_e\left(a\right)·e^{a/}{}^{\eta }=2.22x{10}^{14}kg/m^3$ 1 resulting that:$(d_i/\eta )~T_i$ .

At low temperatures, because the magnetic moment results–according to CGT–by the energy of etherono–quantonic winds of the quantum vacuum, we may take$f_{\mu }\approx 1$ . For the kernel of a formed particle, because the superdense centroids of quasi–electrons are contained (quasi)integrally inside its impenetrable quantum volume ui , we may approximate that–for a protonic m–quark with$N_q\approx 756$ quasi–electrons with the centroids included in the quark’s impenetrable quantum volume of radius$r_q\approx 0.21fm$ , we have$d_e\left(T_i\right)\approx 0.02fm$ at$T_i\approx T_B$ .

Considering that at$T_i<<T_B$  , (for example–at$T_i{}^p\approx 1K$ ), the pre–cluster’s collapse is stopped at$d_i\approx 0.02fm$ , with$f_{\mu }\approx 1$ it results that${\rho }_r{}^0\left(T_i\right)/{\rho }_e{}^0={\rho }_r{}^p\left(T_e\right)/{\rho }_e{}^0\approx (d_i{}^p/\eta )\approx 0.02$ . Because${\rho }_r{}^0\left(T_i\right)/{\rho }_e{}^0\le 1$ , it results that the cluster cannot be equilibrated at an inter–distance$d_i\ge \eta =0.96fm$ ,^2–4 (<$d_i=\eta$  being close to but higher than $d_i\approx \left({}^2{/}_3\right)a$ –corresponding to c)–case), so the conclusion that the mean inter–distance d_i=a between the electrons of the gammonic pre–cluster is one of un–stable equilibrium, is justified.

It results that–at temperatures$T_i<T_B$ , the resulted pearlitic pre–clusters with radius$r_c<r_p$ may collapse because the residual (reciprocal) magnetic moments of the gammons and because the decreasing of the internal energy: $P_{0}V\left(r_c\right)$ more than the superficial energy:${\sigma }_{\gamma }S\left(r_c\right)$ , from equation (3) resulting that:$\left(r_c/r_p\right)<1\Rightarrow P_0\cdot V\text{'}<{\sigma }_{\gamma }S\text{'},(\text{'}=d/dr)$ . Because the electron is a very stable particle, its negentropy being maintained by the energy of the etherono–quantonic winds according to CGT and in concordance with the particle’s “hidden thermodynamics”,¹² it results a slow variation of${\rho }_r{}^0$ with the internal temperature T_i , of the fraction${\rho }_r{}^0\left(T_i\right)/{\rho }_e{}^0\approx (d_i/\eta )$ , but with the consequence of inflation generating or of collapsing of the gammonic pre–cluster, at high variation.

The repulsive force increasing with the temperature T_i may be approximated by a relation specific to metals. Considering that the value${\rho }_r{}^0\left(T_i\right)\approx {\rho }_e{{}^0}^{ }\approx 2.22x{10}^{14}kg/m^3$ is attained at a temperature close to those of quarks deconfining:$T_q\approx 2x{10}^{12}K$ , it results an approximation relation of${\rho }_r$ –density variation with the temperature:

$\begin{array}{l}\frac{\Delta {\rho }_r(d_i)}{{\rho }_r^p(d_i^p)}\approx {\alpha }_c\Delta T\text{; }\frac{{\rho }_e^0}{{\rho }_r^p}=f_{\mu }\frac{d_i}{{\eta }_e}\approx \frac{\text{1}}{\text{0}\text{.02}}={\alpha }_{\text{c}}{\text{(T}}_{\text{q}}{\text{-T}}_{\text{i}}^{\text{p}}\text{)}\approx {\alpha }_c\cdot T_q\\ {\text{T}}_{\text{i}}^{\text{p}}\approx \text{1K ; }{T}_q=2x{10}^{12}K\text{;}\Rightarrow {\alpha }_{\text{c}}\approx \text{2}{\text{.5x10}}^{\text{-11}}{K}^{-1}\end{array}$ (17)

with${\rho }_r{}^p\left(T_B\right)\approx 0.02{\rho }_e{}^0$ resulting:${\alpha }_c\approx 2.5x{10}^{-11}{K}^{-1}$ . So, we may approximate that$f_d\approx (1-{(F_r/F_{\mu })}_a)\approx 0.98$ . At very low temperatures T_i the repulsive force F_r is maintained–according to equations (7), (13) & (17), because the maintaining of the ‘zeroth’ vibrations of the electronic superdense kernels (centroids) which creates the disturbance which generates the scalar density part:${\rho }_r{}^0\left(T_i\right)$ , according to CGT. This phenomenon explains the fact that the quasi–crystallin cluster of electronic centroids of the particle’s kernel not collapses neither at very low temperatures, explaining the particle’s lifetime increasing with the temperature’s decreasing.^2–5

If the internal pre–cluster’s temperature T_i is maintained close to the metastable equilibrium value$T_i{}^e=T_B$  , the pre–cluster’s collapsing may still occur in a strong magnetic field, by the aid of the magneto–gravitic potential $V_{MG}(r_{\varphi })$ , according to CGT.⁸

This conclusion may be argued by the hypothesis of the magnetic fluxon${\varphi }_0=h/2e\approx 2x{10}^{-15}Wb$ , considering that the${\xi }_B$ –vortex–tubes of the B–field are fluxon${\varphi }_0$ with a section radius$r_{\varphi }$  , with a linear decreasing of the impulse density:$p_c=\rho \left(r\right)·(\omega ·r)=\rho \left(r\right)·c~r^{-1}$ , for$r\le r_{\varphi }$ , (which is specific to vortex–tubes) and with the mean density:${\rho }_{\varphi }$ approximate equal with those resulted from the local B_l–field value given by equation (2).

Assuming–by CGT,^2–4 that the vortex–tubes${\xi }_B$ of the magnetic B–field are formed around vectorial photons (vectons) of 2.7K microwave radiation of the quantum vacuum–identified in CGT as electric field quanta having a gauge radius:$r_v\approx 0.41a=0.578fm$ ⁴ and that the electron has a small impenetrable quantum volume:${\upsilon }_i{}^e=1.15x{10}^{-4}f{m}^3$ ,⁵ from CGT⁸ it results that:

$\begin{array}{l}{\text{V}}_{\text{MG}}\text{(r) }=\frac{{\upsilon }_i}{\text{2}}{\rho }_{\phi }(r)\cdot c^2=\frac{{\upsilon }_i{c}^2}{\text{4}\pi \text{ r}}\sqrt{\frac{m_{\phi }\cdot B(R)}{k_1\cdot c}}=\frac{{\upsilon }_i\cdot c}{\text{4}\pi k_1\cdot \text{r}}\sqrt{{\phi }_{0}B(R)}\text{; }{\rho }_{\phi }\text{(r)}={\rho }_{\phi }^{\text{0}}\frac{{\text{r}}_{\text{v}}}{\text{r}}=\frac{m_{\phi }}{2\pi \cdot r_{\phi }}\frac{\text{1}}{\text{r}}{\text{ ; m}}_{\phi }=2\pi {\rho }_{\phi }^0{r}_v{r}_{\phi }\text{;}\\ {\text{V}}_{\text{MG}}\text{(r)}={\text{K}}_{\text{M}}\frac{\sqrt{\text{B(R)}}}{\text{r}}{\text{ ; K}}_{\text{M}}=\frac{{\upsilon }_{\text{i}}^{\text{e}}\cdot c}{\text{4}\pi k_1}\sqrt{{\phi }_0}=\text{7}{\text{.87x10}}^{\text{-40}}\left(\frac{\text{J}\cdot \text{m}}{\sqrt{\text{T}}}\right){\text{; r}}_{\phi }=\sqrt{\frac{m_{\phi }{k}_1\cdot c}{B(R)}}=\sqrt{\frac{{\phi }_0}{B(R)}}\end{array}$ (18)

with ($m_{\varphi }=4.27x{10}^{-14}kg/m$ –the fluxon’s mass on unit lengt). For$l_i=N^{-1/3}=r_{\varphi }$ , we have: $V_{MG}(r_{\varphi })=({\upsilon }_i{}^e·c)B\left(R\right)/4\pi k_1=1.76x{10}^{-32}B\left(R\right)$ –a neglijible value comparative to:$V_{\mu }={\mu }_{e}xB, ({\mu }_e={\mu }_{PB})$ , but which can initiates the clusterizing process of a preonic $z^0$ –pre–cluster forming or of an photon or of an electron forming–around a superdense kernel (half of an electronic neutrino–in the electron’s case, according to CGT),^1–3 but at high values of the B–field or of magnetic field–like etherono–quantonic vortexes formed in the quantum vacuum as chiral fluctuations.

The necessity of a high value of the B–field–like chiral fluctuations intensity in the process of particles cold forming directly from the primordial “dark energy”, results in accordance with a particle–like sub–solitons forming condition¹³ which specifies that the energy$E_{\Gamma }=m_{\Gamma }{c}^2$ of the mass–generating chiral soliton field, (given–in this case by a sinergono–quantonic vortex${\Gamma }_{\mu }={\Gamma }_A+{\Gamma }_B=2\pi r\cdot c$ ), should be double, at least, comparing to the mass energy:$E_m=m{c}^2$ of the generated sub–solitons; ($E_{\Gamma }\ge 2E_m$ ).

The generalization to the scale of an atomic nucleus permits to consider an atomic nucleus as a (non–collapsed) fermionic condensate with quasi–crystallin arrangement of nucleons, which may explain the nucleonic “magic” numbers of maximal stability,^2–4 the nuclear fission reactions–well described by the droplet nuclear model, being explained by a nuclear local phase transformation at the internal temperature increasing–determined by the nucleons’ vibrations.

Mathematically this phenomenon may be equated by equation (11), by modifying the volume term:$E_V=a_{v}A$  and the surface term$E_{\sigma }=a_S{A}^{2/3}$ from the Bethe–Weizsäcker semi–empiric formula of the nuclear binding energy, based on the liquid drop model proposed by George Gamow, in which A is the atomic number and $a_{V }=E_b–\left({}^3{/}_5\right){\epsilon }_F\approx 15.8MeV\approx a_S=17.8MeV$ –the volume and the surface term coefficiens, given as difference between the binding energy of the nucleons to their neighbours:$E_b\approx 40MeV$  and $E_k=\left({}^3{/}_5\right){\epsilon }_F$ –the kinetic energy per nucleon, depending on its Fermi energy.

A generalized form of the binding energy formula for a gammonic BEC, may be obtained writing the kinetic term Ek in the form: k_BT_v, which gives:

${\text{ E}}_N\approx E_b\cdot \left(A-A{}^{\frac{2}{3}}\right)\left(1-\frac{E_k}{E_b}\right);\frac{E_k}{E_b}=\frac{{\text{T}}_{\text{v}}}{{\text{T}}_{\text{C}}}\text{; E}={\text{k}}_{\text{B}}\text{T}$  (19)

with T_C=E_b/k_B and Ev=kBTv–the mean vibration energy of the particles and Eb–the binding energy per particle. The vibrations induced by interaction particles such as a neutron which can split an uranium nucleus, may explain by equation (19), the fact that the nuclear fission is explained by the “drop” nuclear model, even if the nuclear properties and even the nuclear “magic” numbers of nucleons which gives the maximal nuclear stability: 2, 8, 20, 28, (40), 50, 82, 126, may be explained also by a solid rotator type of nuclear model , particularly–of quasi–crystallin type, as those deduced in CGT^2–4 which explains the “magic” nuclear numbers as resulting from quasi–crystalline forms of alpha particles, with$Z={\displaystyle \sum \left(2n^2\right),(n\in N)}$ .

In CGT, this phenomenon is equated by multiplying the binding energy between two nucleons with a term depending on the vibration “liberty” (amplitude) of the nucleon, in the form: $E_b\left(T_v\right)=E_b^0·e_v^{{{}^{-l}}^{/}{}^{\eta *}}\approx E_b^0·\left(1-k_B{T}_v/E_b^0\right)$ , with$l_v~k_B{T}_v$  .

For a gammonic BEC, the number A of degenerate electrons results in the form:

$A_e\approx (4\pi r_p{}^3/3)·N_0=(4\pi /3){\left(r_p/a\right)}^3, \left(N_0=1/a^3\right),$

the equations (12) & (19) , for a metastable gammonic BEC, giving the binding energy in the form:

${\text{E}}_N\approx E_b\cdot \left\{\frac{4\pi }{3}{\left[\frac{T_C}{T_v}\left(1-\frac{T_v}{T_C}\right)\right]}^3-{\left(\frac{4\pi }{3}\right)}^{\frac{2}{3}}{\left[\frac{T_C}{T_v}\left(1-\frac{T_v}{T_C}\right)\right]}^2\right\}\left(1-\frac{T_v}{T_C}\right);$ (20)

with$E_b\approx E_m\approx f_d·m_e{c}^2; T_C\approx f_d·m_e{c}^2/k_{B,} (f_d\approx 0.98)$ , the relation (20) showing that the increasing of the BEC’s temperature determines transition to a liquid/like phase and thereafter–pearlitization, as consequence of the internal temperature increasing over the equilibrium value.

By the paper it is argued that the particles cold forming from quantum vacuum fluctuations–considered in the quantum mechanics, is possible at $T\to 0K$ , but usually by clusterizing, in specific conditions, as a “step–by–step” process in which the intrinsic rest mass/energy necessary for the particles forming: mc², is acquired either by an initial quantum vortex corresponding to an intense magnetic–like field, with vortexial energy comparable with those of the ulterior formed particle and with the producing of a dense kernel which may stabilize the quantum vortex, or by a less intense vortex but enough strong for increase locally the density of formed gammons or z⁰(34m_e) preons.

The vortex was identified as the logical way to explain the fermions pairs forming also in other theoretical models,¹³ but a vortex of etherons with the mass of ${10}^{-60}÷{10}^{-69}kg$ –considered as particles of the sub–quantum medium, (corresponding to the ‘dark energy’ concept), is not enough to explain the possibility of fermion forming from quantum vacuum, without a quantonic component, with quantons of energy $\epsilon =h·1$ ¹⁴ and having superdense centroids which–by vortexial confining, can form a superdense centroid and a rest mass of the formed fermion. According to CGT,^1–5 this mechanism may explain the background radiation (2.7K) photons forming as pairs of vectorial photons, in the Cold ProtoUniverse.

The possibility to explain the masses and the magnetic and electric properties of the elementary particles resulted from the cosmic radiation, in a preonic model, by a cold clusterizing process and with only two quasi–crystallin basic bosons: z₂=4z⁰ =136m_e; z_p=7z⁰ =238m_e, indicates–in our opinion, that after the electrons (negatrons and positrons) cold forming, the clusterizing was the main process of the particles forming in the Universe, by at least two steps: a)–the quasi–crystallin pre–cluster forming (of gammons or of formed z⁰–preons or z₂–and z_p–zerons) and b)–the pre–cluster’s cold collapsing, without destruction, with the maintaining of a quasi–crystallin arrangement of electronic centroids at the kernel’s level, as consequence of their ‘zeroth’ vibrations–which determines an internal scalar repulsive field.

As secondary, particular possibility, the particles forming by pearlitizing supposes the forming of a bigger BEC of gammons, with the concentration of particles:$N_0\approx 1/a^3=3.57x{10}^{44}$ , (a=1.41 fm), in a strong gravitational or magnetic field and at very low temperature and the BEC’s fragmenting by the temperature oscillation around the transition value T_B. and thereafter–the cold collapsing of the resulted pre–clusters, without their destruction. We suppose that this model of particles cold forming may explain a part of the dark matter.

In conclusion, the resulted explicative model of particles cold genesis may explain the existence of a huge number of material particles in the Universe, by the conclusion of cold (“dark”) photons and thereafter–of electronic neutrinos and cold electrons genesis in the Cold Proto–Universe’s period, by chiral (vortexial) fluctuations in the ‘primordial dark energy’–considered in CGT as omnidirectional fluxes of etherons and quantons circulated through a brownian part of etherons and quantons.

None.

Author declares there is no conflict of interest.

1. Arghirescu M. The Cold Genesis– A New Scenario of Particles Forming. Physics & Astronomy International Journal. 2017;1(5):1–5.
2. Arghirescu M. A Cold Genesis: Theory of Fields and Particles. viXra; 2012. p. 1–108.
3. Arghirescu M. The Cold Genesis of Matter and Fields. USA: Science Publishing Group; 2015. p. 1– 222.
4. Arghirescu M. A Quasi–Unitary Pre–Quantum theory of Particles and Fields and some Theoretical Implications. International Journal of High Energy Physics. 2015;2(1):80–103.
5. Arghirescu M. A preonic quasi–crystal quark model based on a cold genesis theory and on the experimentally evidenced neutral boson of 34me. Global Journal of Physics. 2016;5(1):496–504.
6. Krasznahorkay JA, Csatlós M, Csige L, et al. Observation of Anomalous Internal Pair Creation in 8Be: A Possible Signature of a Light, Neutral Boson. UAS: Cornell University Library; 2015. p. 1–5.
7. Arghirescu M. The Explaining of the Elementary Particles Cold Genesis by a Preonic Quasi–Crystal Model of Quarks and a Pre–Quantum Theory of Fields. International Journal of High Energy Physics. 2018;5(1):12–22.
8. Arghirescu M. The Possibility of Particles Forming from a Bose–Einstein Condensate, in an Intense Magnetic or Gravitational Field. International Journal of High Energy Physics. 2018;5(1):55–62.
9. Arghirescu M. A Revised Model of Photon Resulted by an Etherono–Quantonic Theory of Fields. Open Access Library Journal. 2015;2(10):1–9.
10. Hau LV, Harris SE, Dutton Z, et al. Ultra–slow, stopped, and compressed light in Bose–Einstein condensates gas. Nature. 1999;397(594):1–368.
11. Harris SE, Hau LV. Nonlinear Optics at Low Light Levels. Physical Review Letters. 1999;82(23).
12. de Broglie L. La thermodynamique“cachee” des particules. Ann de l’IHP Secttion A. 1964;1(1):1–20.
13. Kiehn RM. The Falaco Effect, A Topological Soliton.USA: Talk at ’87 Dynamics Days; 1987.
14. Şomăcescu L. Electromagnetism and gravity in a unitary theory. Sweden: International Conf. of Gravitation; 1986.