We investigate the critical properties of the Majority-Vote model (MVM) one-dimensional (1D) on directed small-world networks. The MVM is studied by applying the Monte Carlo method. We calculate the critical points, as well as the critical exponent's ratio, and. We find that MVM presents identical exponents to the Ising model one-dimensional on directed Small-World networks (DSW). Our results are in agreement with the Grinstein criterion for models with up and down symmetry on regular lattices.

Keywords: Majority-vote, networks, monte Carlo simulations

Grinstein et al.¹ argue that non-equilibrium spin systems on square lattices (SL) with up-down symmetry belongs to the same class of universality of the Lenz-Ising model in two dimensions (2D). This hypothesis was endorsed for some non-equilibrium models on other regular lattices.²⁻⁸

In 1992 Oliveira⁹ proposed the a non-equilibrium model known as MVM which disobeys the detailed balance. The update of the MVM follows a Markov sequence of stochastic dynamics with local rules and with up-down symmetry. In 2D, on a square lattice, the MVM presents a continuous phase transition with critical exponents identical⁹ of the Ising model¹⁰. Sousa¹¹ and Brenda¹² studied the Ising model and MVM on DSW random lattices, respectively. The exponents obtained in both models are identical and in agreement with the conjecture suggested by Grinstein et al.¹

In this paper, we consider the MVM in 1D on DSW networks and perform an extensive computer simulation study of the MVM. To extract the critical exponents, we applied finite-size scaling (FSS) techniques. Monte Carlo simulations of this system were performed using a master equation to update the spins. Here, there is a continuous phase transition for $0\text{<p}\le 1,$ where p is the rewiring probability. Besides, the calculated critical exponents for p=0.1 do not belong to the same universality class as the 2D Ising model.

We consider the non-equilibrium MVM on DSW networks by a set of spins variables ${\sigma }_i$ assuming values values $\pm 1$ located on every node i of a DSW networks with L sites, where L is the length of a linear chain. The small-world network in one-dimension is built from a regular network with two closest neighbors, connected to L nodes and J neighbors. In this network, each node is randomly reconnected with n edges with probability p. When p = 0 for the network it is regular (received no long-range connection), but for 0 <p <1 the network is small world (short-range links) and p = 1 random network (long-range connections), as shown in Figure 1.

In the MVM on a network, the system dynamics traditionally is as follows: We assign a spin variable ${\sigma }_i$ with values $\pm 1$ at each node of the net. At each step, we try to spin- flip a node. The flip is accepted with probability

                          $w_i\left(1-2q\right){\sigma }_i.S=\frac{1}{2}\left(1-\left({\displaystyle \sum }_J{\sigma }_J\right)\right)$                                                               (1)

where S(x) is the sign of x if $x\ne 0$ , S(x)=0 if x=0. To calculate$w_i$ our sum runs over the (J=2) nearest neighbours of spin i on the network. In this model, we add a long-range connection connecting to another site k with p=0.1. This connection is only one way, that is, the site k does not send back a connection to the site i. $w_i$ means that with probability (1-q) the spin will adopt the same state as the majority of its neighbours. The control noise parameter $q\left(0\le q\le 1\right)$ works like the temperature in the Ising model: the smaller the value of q, the greater the likelihood of parallel alignment with the local majority. The simulations have been performed on different DSW networks sizes comprising a number L=5000, 10000, 20000, 40000, 60000, 80000, 120000, 160000, 200000, and 2600000 of sites. For each L size quenched averages over the connectivity disorder are approximated by averaging over independent realizations. For each simulation, we have started with a stable configuration of spins. We ran $3\times {\text{10}}^5$ Monte Carlo steps (MCS) per spin with $2\times {\text{10}}^5$ configurations discarded for thermalization using a` random-number generator.

Figure 1 Random networks.

The molar magnetization, $\text{m=}{\displaystyle {\sum }_i{\sigma }_i}/L,$ were measured. From magnetization, we can obtain other measures such as the average magnetizsation, susceptibility and the fourth-order Binder cumulant,

                                                                   $\text{m=}{\left[\langle m\rangle \right]}_{\text{av}},$                                                                                          (2)

                                                                     $\chi \left(q\right)=\frac{N}{T}{\left[{\langle m^2\rangle }_{av}-{\langle m\rangle }_{av}^2\right]}_{av}$                                                      (3)

,                                                                       $U_4\left(q\right)=1-\frac{{\langle m^4\rangle }_{av}}{3{\left[\langle m\rangle \right]}_{av}^2}$                                                                     (4)

in the above equations <...> stands for thermodynamic averages and $\mathrm{...}{\left[\mathrm{...}\right]}_{\text{av}}$ for averages over different realizations.

In order to calculate the exponents of these models, we apply finite-size scaling (FSS) theory. We then expect, for large system sizes, an asymptotic FSS behavior of the form

                                                                     $\text{m}=L^{-\beta /\nu }{f}_m\left(x\right)\left[1+\mathrm{...}\right],$                                                         (5)

                                                                      $\chi =L^{\gamma /\nu }{f}_{\chi }\left(x\right)\left[1+\mathrm{...}\right],$                                                           (6)

Where $\beta$ and $\gamma$ are the usual critical exponents, and $f_i\left(x\right)$ are FSS functions with

                                                                      $x=\left(q-q_c\right)L^{1/\nu }$                                                                         (7)

being the scaling variable. The dots in the brackets [1+...] indicate corrections-to-scaling terms. We calculated the error bars from the fluctuations among the different realizations. Therefore, from the size dependence of m and $\chi$ we obtain the exponents ratios $\text{β/ν}$ and $\gamma \text{/ν}$ respectively. The susceptibility at its maximum also scales as $L^{\gamma \text{/ν}}$ . Moreover, the value of $T^0=T_c\left(L\right)$ for which $\chi$ has a maximum scales with the lattice size as

In this way, Eq. 7 may be used to get $1/\nu$ .⁷

In the Figure 2, we plot the magnetization , Binder Cumulante, and susceptibility versus the noise parameter q for sizes L=5M, 10M, 20M, 30M, 40M, 60M, 80M, 120M, 160M, 200M, and 260M and rewiring probability p=0.1. The shape of these figures indicates that this model exhibits a continuous phase transition.

In the Figure 3, we plot logarithm of the magnetization at $q_c$ versus $InL$ for p=0.01 and of the eq. (5), we obtain the exponents ratio $\beta /\nu =0.218\left(11\right)$ .

In the Figure 4, we plot logarithm of the susceptibility $\chi$ at $q_c$ and ${\chi }_{\max }$ versus $InL$ . Of the eq. (6), we obtain the exponents ratio $\gamma /{\nu }_{q_c}=0.535\left(7\right)$ , and $\gamma /{\nu }_{q_{\max }}=0.533\left(8\right)$ for $p=0.1$ .

In the Figure 5, we plot the log-log of $\left[q_c\left(L\right)-q_c\right]$ versus L and the eq. (7), we obtain the exponents ratio $1/\text{ν=}0.\text{51}\left(3\right)$ .

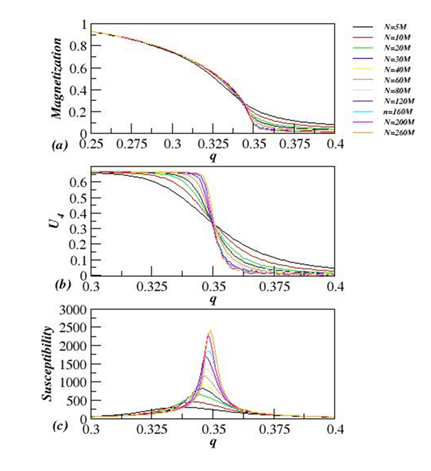
Figure 2 Plot of the magnetization (A) Binder Cumulant (U₄) (B) and susceptibility $\chi$ (C) as a function of the noise parameter q and for sizes L=5M, 10M, 20M, 30M, 40M, 60M, 80M, 120M, 160M, 200M, and 260M with rewiring probability p=0.1. Here 1M=1000.

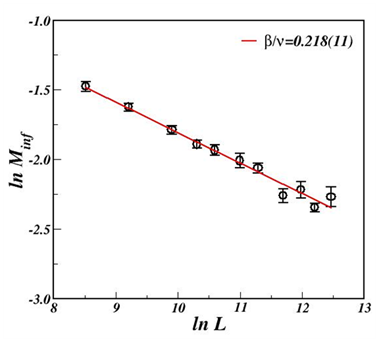
Figure 3 Plot of the logarithm of the magnetization at q_c as a function of the logarithm of L. noise parameter p=0.1.

Figure 4 Plot of the logarithm of the susceptibility ${\chi }_{q_c}$ and ${\chi }_{max}$ versus ln L and noise parameter p=0.1.

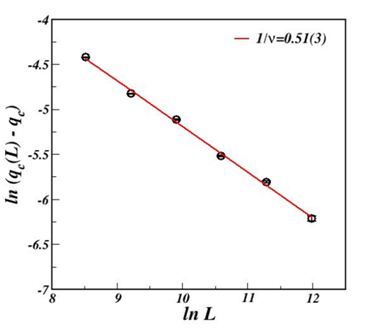
Figure 5 Plot of the $ln\left[q_c\left(L\right)-q_c\right]$ versus ln L and noise psrameter p=0.1.

In the present work, we have shown that, by considering the ferromagnetic MVM in one-dimension on DSW networks there is a continuous phase transition. The exponents ratio $\beta /\text{ν=}0.\text{218}\left(11\right)$ ,$\gamma /{\nu }_{q_c}=0.\text{535}\left(7\right)$ and $1/\text{ν=}0.\text{51}\left(3\right)$ for p=0.1 indicate that they are identical from Ising model in one-dimension on DSW networks.¹³ Therefore, our results agree with the Grinstein criterion for DSW networks.

The author would like to thank the Brazilian agencies CNPq and Capes.

The author states that there is no conflict of interest.

1. G Grinstein, C Jayaprakash, Yu He. Statistical Mechanics of Probabilistic Cellular Automata. Phys Rev Lett. 1985;55,:
2. CH Bennett. Role of Irreversibility in Stabilizing Complex and Nonergodic Behavior in Locally Interacting Discrete Systems. Phys Rev Lett. 1985;55:657.
3. JS Wang, JL Lebowitz J. Phase transitions and universality in nonequilibrium steady states of stochastic Ising models. Stat Phys. 1988;51(5−6):893−906.
4. MC Marques. Nonequilibrium Ising model with competing dynamics: A MFRG approach. Phys Lett A. 1990;145(6−7):379−382.
5. HWJ Blote, JR Heringa, A Hoogland, et al. Stability of Ising systems against non-hamiltonian, symmetry breaking dynamics. Int J Mod Phys B. 1991;5(4):685−695.
6. JM Gonzalez-Miranda, PL Garrido, J Marro, et al. Nonequilibrium phase diagram of Ising model with competing dynamics. Phys Rev Lett. 1987;59:1934.
7. FWS Lima. Majority-vote model on (3, 4, 6, 4) And (3⁴, 6) Archimedean Lattices. Int J Mod Phys C. 2006;17(9):1273−1283.
8. JC Santos, FWS Lima, K Malarz. Majority-vote model on triangular, honeycomb and Kagomé Physica A. 2011;390(2):359−364.
9. MJ de Oliveira. Isotropic majority-vote model on a square lattice. Journal of Statistical Physics. 1992;66(1-2):273−281.
10. RJ Baxter. Exactly solved models in statistical mechanics. London: Academic Press; 1982. p. 502.
11. EM Sousa, FWS Lima. Ising model on directed small-world Voronoi Delaunay random lattices. European Physical Journal Plus. 2013;128:150.
12. Brenda RSC, FWS Lima. Majority-vote model on directed Small-World-Voronoi–Delaunay random lattices. Int J Mod Phys C. 2018;29(7):29
13. FWS Lima. Ising Model in One-Dimensionalon Directed Small- World Networks. RMES. 2017;3(1):553.