Kaluza-klein cosmological models with barotropic fluid distribution

doi:10.15406/paij.2017.01.00018

eISSN: 2576-4543

Physics & Astronomy International Journal

Research Article Volume 1 Issue 3

Kaluza-klein cosmological models with barotropic fluid distribution

Mohammad Amjad Hossain,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Mohammad Moksud Alam,¹ AHM Mahbubur Rahman¹

¹Department of Mathematics, University of Chittagong, Bangladesh
²Department of Mathematics and Natural Sciences, BRAC University, Bangladesh

Correspondence: Mohammad Moksud Alam, Department of Mathematics, University of Chittagong, Bangladesh

Received: August 23, 2017 | Published: October 5, 2017

Citation: Hossain MA, Alam MM, Rahman AHMM. Kaluza-klein cosmological models with barotropic fluid distribution. Phys Astron Int J. 2017;1(3):98-103. DOI: 10.15406/paij.2017.01.00018

Download PDF

Abstract

Kaluza-Klein cosmological models have been investigated for barotropic fluid distribution with time dependent gravitational constant and cosmological constant in the context of general relativity. We have used Hybrid Expansion Law (HEL), a product of power-law and exponential type of functions, to obtain determinate solutions of the Einstein’s field equations. In this paper, we have mainly discussed the graphical behavior of the results for three different cases of interest in modern cosmology.

Keywords: Kaluza-Klein cosmology, cosmological constant, barotropic fluid, hybrid expansion law

Introduction

From astronomical observations, the $2.72548 \pm 0.00057 K$ ¹ isotropic microwave background radiation (CMBR) motivated many researchers to explore the FRW metric with a two-fluid source.²^–⁴ The radiation field corresponding to the experimental CMB radiation is one of the fluids preferred while another is a perfect fluid represent by the matter content of the Universe.⁵ Recently, many researchers investigated different aspects of FRW cosmological models and Kaluza-Klein cosmological models⁶^–¹⁰ in the context of f(R,T) theory of gravity. Higher dimensional plane symmetric cosmological models studied by Mete et al.¹¹ and Amirhashchi et al.¹² also conferred interrelating two-fluid viscous dark energy models in a non-flat Universe. In particular, Samantha & Debata et al.,¹³ have considered two-fluid cosmological models in Kaluza-Klein space-time.

The Kaluza-Klein theory was led to unify Maxwell’s electromagnetic theory and Einstein’s gravitational theory by counting the fifth dimension.¹⁴ Kaluza¹⁵ has revealed that General Relativity (GR) when construed as a vacuum 5D theory contains four-dimensional GR in the existence of electromagnetic field, unruffled with Maxwell’s electromagnetism. To this problem, Kaluza proposed that – GR is not modified, just extended to five dimensions, and there is no physical dependence on the fifth dimension. Klein¹⁶ recommended the compactification of the fifth dimension. Chodos and Detweiler et al.,¹⁷ have shown in their five dimensional models that the extra dimension contracts for cosmic evolution.

Einstein’s field equations are highly nonlinear differential equations. It is not easy to understand what qualitative type of solution they might possess. After the cosmological constant was introduced into general relativity, many cosmologists believe that the simplest candidate for the dark energy is the cosmological constant or vacuum energy. The cosmological constant Λ and phantom fields are violating weak energy conditions $p + ρ > 0$ ¹³ On the other hand this cosmological constant always suffers from the theoretical problems – ‘fine-tuning’ and ‘cosmic coincidence’.¹⁸ For this reason, the equation of state (EoS) of dark energy $ω = \frac{p}{ρ}$ where p is the pressure and $ρ$ is the energy density, in the universe transit from $ω > - 1$ to $ω < - 1$ . Steinhardt et al.¹⁹ Caldwell et al.²⁰ have proposed $ω > - 1$ , and Santhi et al.²¹ have proposed $ω < - \frac{1}{3}$ in their recent paper. In general relativity the dynamics of the spatially flat RW spacetime, the fluids with constant EoS parameter $ω > - 1$ give either a power-law expansion of the Universe $a \propto t^{α}$ or an exponential expansion $a \propto e^{β t}$ , where $α, β \geq 0$ are constant.²² The Hybrid Expansion Law (HEL) leads to $β = 0, α = 0$ which are the special cases of the HEL in early universe. Surprisingly, if the $α > 0$ and $β > 0$ leads to a new cosmology ascending from the HEL.

A time variation of the gravitational constant G was first proposed by DiracDirac²³ in his large number hypothesis. Other outstanding solutions were studied by WeinbergWeinberg²⁴ and Padmanabhan²⁵ Cosmological models with time-dependent G and $Λ$ , the relation $Λ \propto a^{- 2}$ (a is the scale factor of the Robertson-Walker metric) and $Λ \propto t^{- 2}$ , were first obtained Bertolami²⁶ Sharif et al.²⁷ Gamal et al.²⁸ and Mukhopadhyay et al²⁹ are some of the authors who have investigated several aspects of Kaluza-Klein cosmology with varying gravitational constant and cosmological constant and also deceleration parameter q. For the range of α, the transition from deceleration to acceleration phase of the universe for HEL take place at $t = (\sqrt{α} - α) / β$ .

There are different cases of interest in modern cosmology, the matter dominated eras, the radiation dominated eras, and stiff fluid eras. In the matter dominated era, the main energy density is that of ordinary matter in galaxies, whose random velocities are small and which therefore behave like dust $p = 0$ . In the radiation dominated era, which is in the early universe, the principal energy density is in radiation or relativistic particles which have an equation of state $p = \frac{1}{4} ρ$ . The cosmological model of Zeldovich³⁰ in which the primordial universe is supposed to be constituted of a cold gas of baryons. For positive energy density in the presence of stiff matter, the primordial universe is singular which begins with infinite density from a state with a vanishing scale factor.

Inspired by the above investigations and discussions, we have studied KK cosmological models with variable G and $Λ$ by taking different barotropic fluid distributions into account. In this work we have 4 sections. Section 2 represents the field equations where the universe filled with perfect fluid. An explicit solution of the equations with graphs is presented in section 3. Graphical discussion and conclusion are given in the last two sections.

Model and field equations

The metric of the Kaluza-Klein cosmology is given by¹⁵

$d s^{2} = d t^{2} - a^{2} (t) [\frac{d r^{2}}{1 - k r^{2}} + r^{2} d Ω^{2} + (1 - k r^{2}) d ψ^{2}]$ (1)

Where $d Ω^{2} = (d θ^{2} + \sin^{2} θ d ϕ^{2})$ and $a (t)$ is the scale factor, $k = - 1, 0, 1$ is the curvature parameter for spatially open, flat and closed universe respectively.

The energy-momentum tensor where the universe is filled with perfect fluid is given by

$T_{i j} = (ρ + p) u_{i} u_{j} - p g_{i j}$ (2)

Where $i, j = 0, 1, 2, 3, 4$ and $u_{i}$ are the components of the five velocity satisfying $u^{i} u_{j} = 1;$ $ρ$ is the energy density and p is the pressure of the cosmic fluid.

The Einstein’s field equations are given by

$R_{i j} - \frac{1}{2} R g_{i j} + Λ g_{i j} = - 8 π G T_{i j}$ (3)

Where $R_{i j}$ , $g_{i j}$ and $R$ are the Ricci tensor, metric tensor and Ricci scalar respectively.

Here, we have considered the gravitational constant G and cosmological constant $Λ$ as a function of time t.

Using equations (1), (2) and (3), we obtain the following two independent equations

$6 (\frac{{\dot{a}}^{2}}{a^{2}} + \frac{k}{a^{2}}) = 8 π G ρ + Λ$ (4)

$- 3 (\frac{\ddot{a}}{a} + \frac{{\dot{a}}^{2}}{a^{2}} + \frac{k}{a^{2}}) = 8 π G p - Λ$ (5)

Equations (4) and (5) reduce to

$6 (H^{2} + \frac{k}{a^{2}}) = 8 π G ρ + Λ$ (6)

$- 3 (\dot{H} + 2 H^{2} + \frac{k}{a^{2}}) = 8 π G p - Λ$ (7)

$H = \frac{\dot{a}}{a}$ is the Hubble parameter and an overhead dot $(.)$ hereafter, denote ordinary differentiation with respect to cosmic time ‘t ’ only.

The usual energy conservation equation $T_{; j}^{i j} = 0$ yields

$\dot{ρ} + 4 H (p + ρ) = 0$ (8)

From (3) by taking the vanishing divergence of the Einstein tensor, we have

$8 π \dot{G} ρ + \dot{Λ} + 8 π G [\dot{ρ} + 4 H (p + ρ)] = 0$ (9)

Substituting (8) in (9) it follows that

$8 π \dot{G} ρ + \dot{Λ} = 0$ (10)

Equation (10) indicates that $Λ$ is a constant whenever G is constant and vice versa.

The equation of state is given by

$p = ω ρ$ (11)

where $ω \in [0, 1]$ is a constant and can take the values 0, $\frac{1}{4}$ , and 1 respectively for the pressure less dust, radiating and stiff or Zel’dovich fluids.

Solution of field equations

The system of equations (6)-(8) and (11) supply only four equations in five unknowns like $a$ , $ρ$ , $G$ and $Λ$ . One extra equation is needed to solve the system completely. Now we consider the following ansatz for the average scale factor of the universe which yields a time dependent deceleration parameter as

$a = c t^{α} e^{β t}$ (12)

where $c > 0$ , $α \geq 0$ and $β \geq 0$ are constants. This generalized form of scale factor is referred to as the Hybrid Expansion Law (HEL) and combines both exponential and power law. We assume $α \geq 0$ and $β \geq 0$ to sustain HEL that leads to a new cosmology. Because of the time dependency, the obtained deceleration parameter exhibits the transition of the universe from the initial decelerating phase to the present accelerating phase. That is why this sort of average scale factor is physically meaningful. Akarsu et al.²² Vijaya Santhi³¹ Pradhan et al.,³² and Yadav³³ are some of the authors who have taken into account the above consideration to investigate different cosmological models.

From equation (12), we have

$H = \frac{\dot{a}}{a} = \frac{α}{t} + β$ (13)

and $\dot{H} = - \frac{α}{t^{2}}$ (14)

From equations (8), (11) and (12), we obtain the energy density

$ρ = \frac{l}{c^{γ} t^{γ α} e^{β γ t}}$ (15)

Where $γ = 4 (ω + 1)$ and $l$ is a constant of integration.

The pressure of the cosmic fluid is

$p = \frac{ω l}{c^{γ} t^{γ α} e^{β γ t}}$ (16)

Adding equations (6) and (7) and hence using equations (13), (14) and (15), the gravitational constant is calculated as

$G = \frac{3}{2 π l γ} [c^{γ} t^{γ α} e^{β γ t} (\frac{α}{t^{2}} + \frac{k}{c^{2} t^{2 α} e^{2 β t}})]$ (17)

Equation (6) gives the cosmological constant as

$Λ = 6 {(\frac{α}{t} + β)}^{2} - \frac{12 α}{γ t^{2}} + \frac{6 k (γ - 2)}{γ c^{2} t^{2 α} e^{2 β t}}$ (18)

The deceleration parameter is

$q = - \frac{a \ddot{a}}{{\dot{a}}^{2}} = \frac{α}{{(α + β t)}^{2}} - 1$ (19)

$q = 0$ when $t = \frac{\sqrt{α} - α}{β}$ where $0 < α < 1$ . At this point of time the expansion velocity has an extreme. Hence the universe expands with decelerated velocity, $q > 0$ , and accelerated velocity and $q < 0$ (inflation), for some t, but q can never be less than -1. This shows a transition from deceleration to acceleration phase of the universe for Hybrid expansion law (HEL). As the deceleration parameter q measures the rate of change of the expansion of the universe, it is considered as the most important observational quantity in cosmology.

From the relation between mean scale factor and red shift $(z)$ , we have

$a (t) = \frac{1}{1 + z}$ (20)

Where the present scale factor $a_{_{0}} = 1$ . Combining (12) and (20), we perform the following calculation to obtain time-red shift relation as shown in.⁸

Now choosing $c = 1$ we can write

$t^{α} e^{β t} = \frac{1}{1 + z}$

Which implies

$t e^{\frac{β t}{α}} = {(\frac{1}{1 + z})}^{\frac{1}{α}}$

Substitute $\frac{β t}{α} = u$ to obtain

$u e^{u} = \frac{β {(\frac{1}{1 + z})}^{\frac{1}{α}}}{α}$

Which follows that

$u = W [\frac{β {(\frac{1}{1 + z})}^{\frac{1}{α}}}{α}]$

Which implies that

$t = \frac{α W [\frac{β {(\frac{1}{1 + z})}^{\frac{1}{α}}}{α}]}{β}$ (21)

Where the Lambert-W function (also called the omega function or product logarithm) is introduced.

By using equations (21) and (19), we can determine the deceleration parameter $q$ which indicates the transition from decelerated to accelerated phase as per observation occurs at some red shift as obtained in.⁸

Discussion

In summary, we have discussed the Kaluza-Klein cosmological model with the barotropic equation of state which exhibits a number of interesting phenomena in different parameter regimes. We have analyzed the variation of various parameters against time graphically for the cosmological models.

(Figure 1) shows that the energy density $(ρ)$ decreases with time and coincides after a certain time at around $t = 0.5$ for different values of $ω$ and keep up a similar trend to the evolution of universe for dust, radiation and stiff fluid era. Figure-2, Figure-3 and Figure-4 show the plot for the variation of the gravitational constant $(G)$ against time for different epochs representing flat , closed and open universes. From those figures, it can be seen that the gravitational constant decreases with time showing similar behavior for $ω = 1 / 4$ and $ω = 1 / 4$ , but sharply decreases for $ω = 1$ . For all three prescribed fluid distributions, $ω = 0, \frac{1}{4}, 1$ , it is noticed from Figure-5, Figure-6 and Figure-7 that the cosmological constant, $Λ$ , approaches zero from negative values with the evolution of the universe marking similarities for $k = 0$ and $k = - 1$ , but the graphs show significant dissimilarities for $k = 1$ .

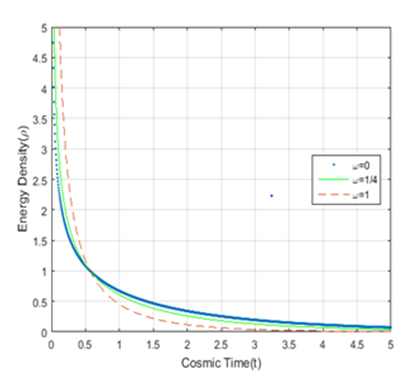
Figure 1 Plot for variation of energy density vs cosmic time; using equation (15). The dotted, solid, and dashed curves $(l = 1, c = 1, α = β = 0.1)$ represent $γ = 4, 5 a n d 8$ respectively.

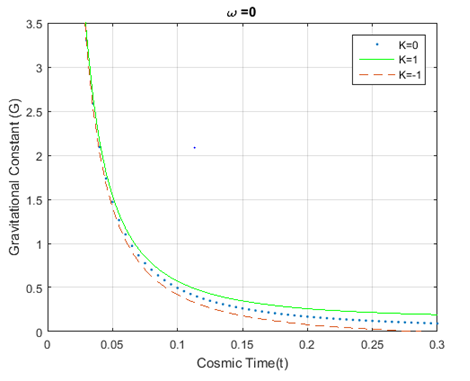
Figure 2 Plot for variation of Gravitational constant (G) vs cosmic time; using equation (17). The dotted, solid, and dashed curves $(l = 1, γ = 4, α = β = 0.1)$ represent $k = 0, k = 1, k = - 1$ respectively.

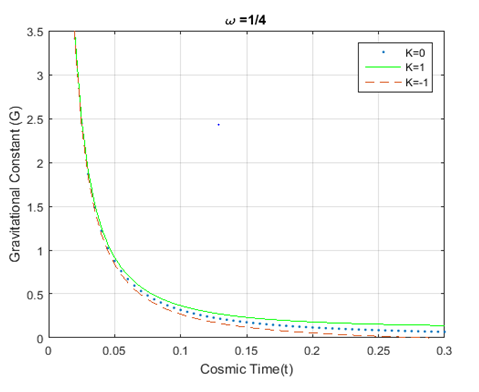
Figure 3 Plot for variation of Gravitational constant (G) vs cosmic time; using equation (17). The dotted, solid, and dashed curves $(l = 1, γ = 5, α = β = 0.1)$ represent $k = 0, k = 1, k = - 1$ respectively.

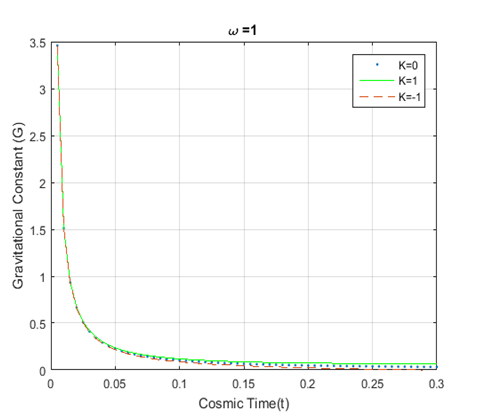
Figure 4 Plot for variation of Gravitational constant (G) vs cosmic time; using equation (17). The dotted, solid, and dashed curves $(l = 1, γ = 8, α = β = 0.1)$ represent $k = 0, k = 1, k = - 1$ respectively.

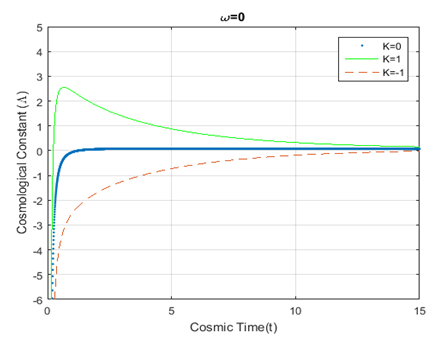
Figure 5 Plot for variation of Cosmological constant $(Λ)$ vs cosmic time; using equation (18). The dotted, solid, and dashed curves $(γ = 4, c = 1, α = β = 0.1)$ represent $k = 0, k = 1, k = - 1$ respectively.

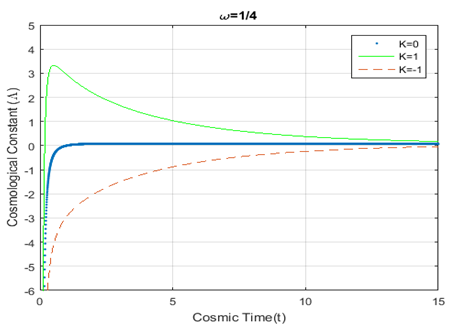
Figure 6 Plot for variation of Cosmological constant $(Λ)$ vs cosmic time; using equation (18). The dotted, solid, and dashed curves $(γ = 5, c = 1, α = β = 0.1)$ represent $k = 0, k = 1, k = - 1$ respectively.

Figure 7 Plot for variation of Cosmological constant $(Λ)$ vs cosmic time; using equation (18). The dotted, solid, and dashed curves $(γ = 8, c = 1, α = β = 0.1)$ represent $k = 0, k = 1, k = - 1$ respectively.

Again we have plotted different cosmological parameters for $k = 0$ , $k = 1$ and $k = - 1$ representing the graphs for $ω = 0$ , $ω = 1 / 4$ and $ω = 1$ in the same coordinate diagram . It is observed from the Figure-8, Figure-9 and Figure-10 that $G (t)$ falls gradually as we move from $ω = 0$ to $ω = 1$ at the same time in Figure-11 , Λ(t) increases when moving from $ω = 0$ to $k = 0, - 1$ and follows reverse order for $k = - 1$ in Figure-13. According to Figure-12, $Λ (t)$ goes up sharply and changes the trend dramatically after a certain age of the universe with the change of epochs. Finally, Figure-14 is a plot of the deceleration parameter against time and shows that the deceleration parameter reaches -1 with the age of the universe. All these graphical results indicate the dependency of the curvature parameter among the fluid distributions and compatibility with the current cosmological observations.

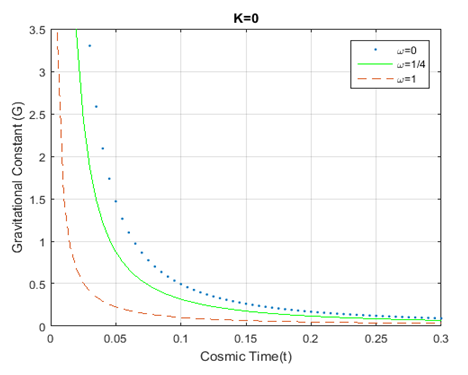
Figure 8 Plot for variation of Gravitational constant $(G)$ vs cosmic time; using equation (17). The dotted, solid, and dashed curves $(k = 0, l = 1, c = 1, α = β = 0.1,)$ represent $γ = 4, 5 a n d 8$ respectively.

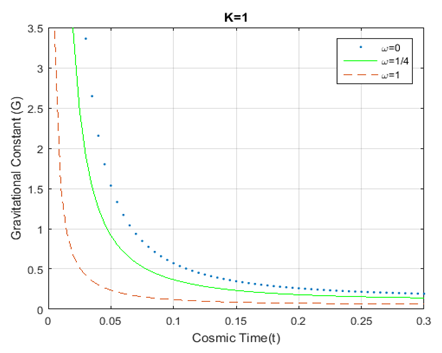
Figure 9 Plot for variation of Gravitational constant $(G)$ vs cosmic time; using equation (17). The dotted, solid, and dashed curves $(k = 1, l = 1, c = 1, α = β = 0.1,)$ represent $γ = 4, 5 a n d 8$ respectively.

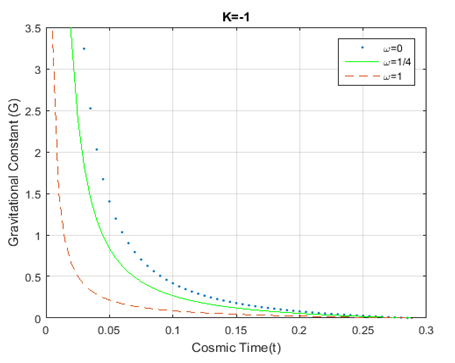
Figure 10 Plot for variation of Gravitational constant $(G)$ vs cosmic time; using equation (17). The dotted, solid, and dashed curves $(k = - 1, l = 1, c = 1, α = β = 0.1,)$ represent $γ = 4, 5 a n d 8$ respectively.

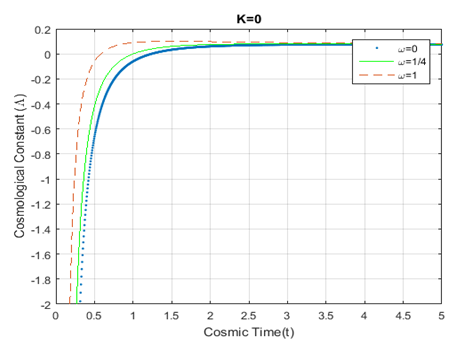
Figure 11 Plot for variation of Cosmological constant $(Λ)$ vs cosmic time; using equation (18). The dotted, solid, and dashed curves $(k = 0, c = 1, α = β = 0.1)$ represent $γ = 4, 5 a n d 8$ respectively.

Figure 12 Plot for variation of Cosmological constant $(Λ)$ vs cosmic time; using equation (18). The dotted, solid, and dashed curves $(k = 1, c = 1, α = β = 0.1)$ represent $γ = 4, 5 a n d 8$ respectively.

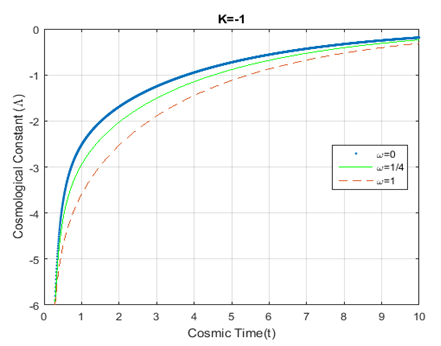
Figure 13 Plot for variation of Cosmological constant $(Λ)$ vs cosmic time; using equation (18). The dotted, solid, and dashed curves $(k = - 1, c = 1, α = β = 0.1)$ represent $γ = 4, 5 a n d 8$ respectively.

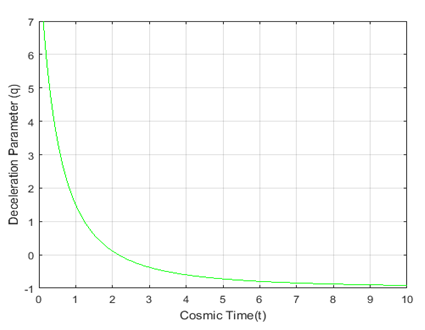
Figure 14 Plot for variation of Deceleration parameter $(q)$ vs cosmic time for $α = β = 0.1$ ; using equation (19).

Conclusion

In this paper, we have investigated the Kaluza-Klein cosmological model with time dependent gravitational and cosmological constant taking the barotropic equation of state into account. We have presented our solutions for the energy density, pressure, gravitational constant and cosmological constant with respect to time t. We have plotted these solutions and discussed graphical features with different fluid distributions for flat and non-flat universe models. It is noticed that the energy density ρ is a decreasing function of time t and ρ approaches zero with the evolution of time. Also we have shown that the gravitational constant is a decreasing function of time as studied in the models by Grøn³⁴ Helling et al.²⁵ and Rowan Robinson³⁶ It is also observed that the cosmological constant is negative throughout the evolution of universe for $k = 0, - 1$ (Figure 11 & Figure 13) irrespective of the barotropic fluid distributions which is termed as an anti-de Sitter phase with cyclic evolution of the universe. On the contrary, the universe enters from anti-de Sitter phase to de Sitter phase within a the short period after Big Bang and remains in that phase with the evolution of universe until the cosmological constant reaches a small positive value for $k = 1$ (Figure 12) which is reasonable for the accelerating expansion of the universe³⁷^–⁴⁰ that we observe at present. Moreover, it can be deduced from equation (19) that the deceleration parameter $q < 0$ when $t > \frac{\sqrt{α} - α}{β}$ . It means that the universe is accelerating because acceleration at certain stage in the evolution of the universe implies $q < 0$ for some time t.