This paper presents the Landau theory of second order phase transitions in terms of the configurational entropy using the connection between this entropy and the order parameter. It is offered a variant of theory, in which the Nernst theorem is obeyed. Within the framework of heterogeneous model the phenomena of growth of level of fluctuations and their correlations are analyzed at transition of critical point as competitions of kinetic and relaxation processes in the conditions of proximity of two critical points.

The Landau theory of second order phase transitions (PT-2) was offered in the middles of previous century,^1,2 but interest to it does not weaken to the present, for example, in phase fields theories.^3–11 By more late researches in the theory of PT-2 very important one-valued connection was set up between the order parameter (OP) and the configurational entropy.¹² Such connection allows choosing as an independent variable one of them. PT-2 was based traditionally on the use of OP, but a variant will be first considered here, in basis of which as an independent variable configurational entropy is fixed.

Connection between the free and internal energy

Let’s set the free energy functional F{φ(x)} for the non-equilibrium state of the system with given OP φ(x) in a form typical for PT-2¹²

$F\left\{\varphi \left(x\right)\right\}=F_0+\frac{1}{2}{\displaystyle \int \left[c{\left(\nabla \varphi \right)}^2+a{\varphi }^2+\frac{1}{2}b{\varphi }^4-2\varphi h\right]dV}$ ,  (1)

Free energy is here presented, actually, as expansion of a functional F{φ(x)} in a series over the small φ(x) and its spatial derivatives. The first term in square brackets is energy of the heterogeneous distribution, h(x) is the external field. The type of dependence on the spatial derivate φ(x) is dictated by considering of a homogeneous and isotropic system. In obedience to ideology of PT-2 the free energy depends on a temperature, however its dependence on a temperature is concentrated only in a coefficient a, which besides changes a sign in a critical point. It is considered that other coefficients do not depend on a temperature at all.

For a homogeneous case

$f\left(\varphi \right)=f_0+\frac{1}{2}a{\varphi }^2+\frac{1}{4}b{\varphi }^4-2\varphi h$ ,  (2)

Here and below the extensive thermodynamic variables are designated by large characters F, S et cetera, and their densities are designated by small characters f, s et cetera. A derivative of the free energy on the temperature differs from entropy by a sign only. As the coefficient a depends on temperature only, than differentiating (2), we get¹²

$s_c=-\frac{df}{dT}=-\frac{\alpha }{2T_c}{\varphi }^2<0$ ,  (3)

where s_c is configurational entropy density, T_c is a critical temperature, the constant α does not depend on a temperature, and is determined by a relation

$a=\alpha \frac{T-T_c}{T_c}$ ,  (4)

where T is the absolute temperature (thermostat). Actually, s_c is not total entropy, but its configurational part only, as pure thermal effects in PT-2 are not explicitly considered. In addition, the relation (3) is not general, but a model. However within the framework of this model a one-valued connection between OP and the configurational entropy is established. It means that it is possible to choose one of these variables as an independent thermodynamic variable and to outline a theory of PT-2, for example, not in terms of OP, but in terms of configurational entropy. Besides, it prompts the idea for application of similar model relations in more wide area (not only for PT-2), including modeling of severe plastic deformation processes. We mark that a similar situation arises up in the theory of vacancies. There Boltzmann offers a formula, uniquely relating the configurational entropy and the vacancy concentration that also allows choosing one of them as an independent variable.¹³ It is possible to conclude from it, that all three variables, configurational entropy, defect concentration and order parameter, in a different form characterize the same structural reality of solid, its defectiveness. In the case of phase transitions the defectiveness obviously can be related to the spontaneous origin of embryos of a new phase. Within the framework of this model relation it is possible to pass in accordance with expression

$F_c=U-T{S}_c$   (5)

from the configurational free energy to the internal energy and vice versa. Here, to underline configurational nature of free energy and entropy, they are supplied a lower index c.

Differentiating (5) we get useful relations

$S_c=-\frac{\partial F}{\partial T}=-\frac{\partial U}{\partial T}-S_c+T\frac{\partial S_c}{\partial T}$   (6)

from which follows

$\frac{\partial U}{\partial T}-T\frac{\partial S_c}{\partial T}=0$   (7)

by virtue of that the derivative of configurational entropy on temperature is the second derivative of the free energy on temperature, but the last depends linearly on the temperature. It is follows from there that both the configurational entropy and the internal energy do not explicitly depend on temperature. Using Eqs. (2) and (5) we find an explicit expression for the internal energy (for a homogeneous case and without the account of the external field)

$u\left(\varphi \right)=f_0-\frac{1}{2}\alpha {\varphi }^2+\frac{1}{4}b{\varphi }^4$   (8)

where already all coefficients do not depend on a temperature at all. It is possible to consider by virtue of generality of result that namely expression (8) is base model relation of theory of PT-2, and temperature dependence of the coefficient a (4) and the free energy (1), (2) is simple consequence of this fact. Indeed, let us consider that simple base relation for internal energy (8), in which all of coefficients do not depend on a temperature, is initially given. In this case ∂U/∂T ≡ 0, and according to (7) ∂S_c/∂T ≡ 0 too. Then configurational entropy can be also presented as a series expansion on OP, limited here quadratic approaching only

$s_c=\frac{1}{2}c{\varphi }^2+\mathrm{...}$   (9)

Substituting it in Eq. (5) and taking into account Eq. (8) we get

$f\left(\varphi \right)=f_0-\frac{1}{2}\alpha {\varphi }^2-\frac{1}{2}cT{\varphi }^2+\frac{1}{4}b{\varphi }^4\mathrm{...}$   (10)

We define coefficient c from a condition that in the critical point T = T_c a total coefficient at φ₂ must be a zero

$c=-\frac{\alpha }{2T_c}$   (11)

Collecting all formulas, we get (2). We mark that in area of small φ in (8) the first term prevails, and the internal energy has a maximum. Therefore for the nonequilibrium states with a zero value OP (T>T_c) the internal energy has a maximum too (curve 1, Figure 1), while the free energy has, as it must be, a minimum (curve 3). At large OP, the second term prevails, and the internal energy has already minimums in non-zero extreme points, determined from a conditions

$\mu =\frac{\partial u}{\partial \varphi }=\varphi \left(-\alpha +b{\varphi }^2\right)=0$   (12)

and equal

${\varphi }_{\mu }=\pm {\left(\frac{\alpha }{b}\right)}^{1/2}$   (13)

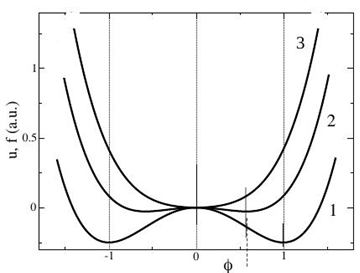
Figure 1 Internal (1) and free (1-3) energies: 1 – at T = 0K; 2 – at T = 200K; 3 – at T = 400K. It is here accepted α = 1, b = 1, T_c = 300K.

Here μ is the “chemical potential” as surplus energy, being on unit of OP. In area of zero OP the internal energy is convex; it is concave in area of non-zero values of OP (13). Inflection points, dividing these areas, are deduced from a condition

$\frac{{\partial }^{2}u}{\partial {\varphi }^2}=-\alpha +3b{\varphi }^2$ ,  (14)

that gives a value

${\varphi }_{\mu }=\pm {\left(\frac{\alpha }{3b}\right)}^{1/2}$   (15)

(it is dotted vertical line in Figure 1). Now we compare positions of extremums of the internal and free energy. For the last they are determined from a condition

$\frac{\partial f}{\partial \varphi }=\varphi \left(a+b{\varphi }^2\right)=0$   (16)

and non-zero roots are equal

${\varphi }_F=\pm {\left(\frac{a}{3b}\right)}^{1/2}={\varphi }_{\mu }{\left(\frac{T_c-T}{T_c}\right)}^{1/2}$   (17)

From where we notice that at a zero temperature non-zero roots of the free and internal energy coincide (their graphs coincide fully, see curve 1 in Figure 1)

${\varphi }_{\mu }=\max \left({\varphi }_F\right)=\pm {\left(\frac{\alpha }{b_c}\right)}^{1/2}\ne 0$   (18)

With growth of temperature non-zero roots of the free energy diminish (curve 2) and in a critical point goes to zero (curve 3). Here they meet with identically zero roots. Higher than critical point expression (17) is lost meaning, and there are only roots of equations (16) identically equal to the zero. If the system is in the non-equilibrium state, it tends to the equilibrium state in accordance with the Landau- Khalatnikov equation (see arrows along to the curve 2, Figure 2).

$\frac{\partial \varphi }{\partial t}=-{\gamma }_f\frac{\partial f}{\partial {\varphi }_c}$   (19)

Figure 2 Internal (1) and free (2) energies at T = 200K, Arrows pointer specify direction of the system evolution along relief of the free and internal energy.

where f is the free energy density, γ_f is a kinetic coefficient. But tending of the system to the equilibrium state it is possible to express and in terms of the internal energy. We must take into account thus that in the equilibrium state the tangent to the graph of the free energy has a zero inclination by definition, while tangent to the graph of the internal energy has a non-zero inclination. Then evolution equation in terms of the internal energy must look like

$\frac{\partial \varphi }{\partial t}=-{\gamma }_u\left(\frac{\partial u}{\partial \varphi }-{\mu }_{eq}\right)$   (20)

where u is the internal energy density, γ_u is a new kinetic coefficient, µ_eq is “chemical potential” in the equilibrium state. Sign a “plus” gets out, if in the equilibrium state the internal energy is convex, sign “minus” if concave (Figure 3). Tending of the system to the equilibrium state in this case is shown by arrows along relief of the internal energy in Figure 2 & 3. Both in terms of the free energy and in terms of the internal energy, the system tends to the same steady-state (Figure 2). It follows from that in a steady-state a condition of equality to zero of right parts of evolution Eqs. (19) and (20) is satisfied at the same agreed solutions (13) and (17). Eq. (20) can be directly deduced from Eq. (19). For this purpose it is enough to substitute (5) in (19) with taking in account (3)

$\frac{\partial \varphi }{\partial t}=-{\gamma }_f\left(\frac{\partial u}{\partial {\varphi }_c}-T\frac{\partial s}{\partial \varphi }\right)=-{\gamma }_f\left(\frac{\partial u}{\partial {\varphi }_c}-\alpha \frac{T}{T_c}\varphi \right)$   (21)

We consider that deviation from the equilibrium state is small, and value of the second term in (21) is little differing from equilibrium. Then, taking the equilibrium value OP from (17), we get

$\frac{\partial \varphi }{\partial t}=-{\gamma }_f\left(\frac{\partial u}{\partial {\varphi }_c}-{\mu }_{eq}\right)$   (22)

Where

${\mu }_{eq}=-\frac{{\alpha }^{1/2}}{b^{3/2}}\frac{T}{T_c}\sqrt{\frac{T_c-T}{T_c}}$   (23)

Expression for μ_eq it is possible to get also, substituting (17) in (12). The curve of its dependence on a temperature is resulted in Figure 4, from which is obvious, that μ_eq always less zero, that however is obvious and from the curve U′ in Figure 3. In addition, from Figure 4 it is obvious that most sharply μ_eq changes at approaching to the critical point. Eq. (22) coincides with Eq. (20), if to consider that kinetic coefficients are connected with a relation

${\gamma }_u={\gamma }_{f}sign\left(u^{″}\right)$   (24)

Figure 3 Internal energy and its derivatives. Vertical line conducted through minimums of free energy (eq1, eq2).

Figure 4 Dependence of the “chemical potential” on the temperature.

The validity of choice of signs in Eq. (20) it is possible to check with help of Figure 3, where the curves of the internal energy and its first two derivatives on OP are resulted only. For illustration the equilibrium states are chosen on the left and on the right of inflection point in area of convex and concavity of the internal energy. If the system is in the non-equilibrium state φ >φ_eq1 (dotted line on the right of eq1 in Figure 3), then

$\frac{\partial u}{\partial \varphi }\le {\left(\frac{\partial u}{\partial \varphi }\right)}_{eq1}$ ,  (25)

and returning force is directed toward diminishing of OP, and the sign in Eq. (20) must be positive. In area of concavity at condition φ>φ_eq2 inequality is just opposite

$\frac{\partial u}{\partial \varphi }>{\left(\frac{\partial u}{\partial \varphi }\right)}_{eq2}$ ,  (26)

and sign in Eq. (20) must be chosen negative. Thus, following connection between the configurational entropy and OP (3), it was succeeded to set connection between the free and internal energy, and to find the alternative form of evolution equations in terms of the internal energy (20). In an order to use evolution equation (20) it is needed to know an equilibrium value of “chemical potential”. For its finding again all the same it is necessary to use a minimum of the free energy (16), in which it is possible to calculate all of descriptions the internal energy and its derivatives.

For a heterogeneous problem a functional of the internal energy by analogy with (1) and with taking in account (8) looks like

$U\left\{\varphi \left(x\right)\right\}=F_0+\frac{1}{2}{\displaystyle \int \left[c{\left(\nabla \varphi \right)}^2-\alpha {\varphi }^2+\frac{1}{2}b{\varphi }^4-2\varphi h\right]dV}$ .  (27)

Evolution equation of type (20) is in this case

$\frac{\partial \varphi }{\partial t}=-{\gamma }_u\left(\frac{\partial u}{\partial \varphi }-{\mu }_{eq}\right)$ ,  (28)

or in an explicit form

$\frac{\partial \varphi }{\partial t}=-{\gamma }_u\left(-c\Delta \varphi -\alpha \varphi +b{\varphi }^3-h-{\mu }_{eq}\right)$ .  (29)

Equation contains algebraic part (sources and sinks) and differential one. If to ignore algebraic part at a negative coefficient c<0 the equation is diffusive type. In such form it can describe the processes of spreading (diffusion) of OP, resulting in its more homogeneous distribution and, consequently, it is favorable for resorption of possible fluctuations. Vice versa, at a positive sign c>0 this equation can describe the processes of strengthening of fluctuations or avalanche-type transition to the new phase. Chemical potential of OP unlike (12) is now determined through a functional derivative

$\mu =\frac{\delta u}{\delta \varphi }=-c\Delta \varphi -\alpha \varphi +b{\varphi }^3-h$   (30)

and it depends on gradient part. At the same time, its equilibrium value μeq must not depend on gradient part, because the equilibrium state is supposed the homogeneous distribution by definition. Therefore an equilibrium value is determined on those formulas (23) as for a homogeneous problem. The evolution equation (29), following from functional of the internal energy (27), as well as evolution equations, followings from functional of free energy (1)¹² can describe relaxation (suppression) of the heterogeneous field of fluctuations. But they do not contain an active constituent, describing the generation of thermal fluctuations (noise). For modeling of this we add an accidental source of OP to right part (29)

$\frac{\partial \varphi }{\partial t}=-{\gamma }_u\left(-c\Delta \varphi -\alpha \varphi +b{\varphi }^3-h-{\mu }_{eq}\right)+n\left(\varphi \right)$   (31)

Thus, if the system is initially in the equilibrium state and a temperature strongly differs from critical one, expression in parentheses in Eq. 31 equals zero for all volume of the system. The origin of thermal fluctuations of OP due to the last term transfers locally the system into separate areas in a non-equilibrium state. Now for these areas expression in parentheses becomes different from zero, and the reaction of the system is directed on suppression of arising up fluctuations. Note that suppression them goes in all of volume due to algebraic part of the evolution equation (rapid process), and additionally due to gradient part on the boundaries of areas (slow process).

At the same time, fluctuations are arisen in other places. The processes of their generation and suppression, which will dynamically counterbalance each other, go in parallel. Actually, thermal fluctuations displace slightly the true equilibrium state of the system, and it will take nature of stationary-state. These processes in vicinity of a critical point, when two (zero and non-zero) steady-states are close to each other, will go quite othergates. Thermal fluctuation can transfer part of volume of the system from one stable state in another stable state. In this case, the volume (rapid) suppression of fluctuation is absent, and there is only slow suppression it on the boundaries of area and the boundary of an area will be gradually reduced. As this process is slow by virtue of dimension factor, long-living fluctuations are arisen. As the process of generation of fluctuations continues with same intensity, and the process of their suppression is strongly slowed, the total number of fluctuations increases, what is observed at PT-2. It is of interest to probe numerically the transition of the system through a critical point on some model example. In view of calculable resource limiting of serial computers we consider the 2D variant of problem. Parameters for calculations the same, as higher (Figure 1), a coefficient at a gradient term is chosen equal c=0.5. All of area with zero OP consists of 100×100 squares of unit sizes. For testing of problem a heterogeneity is entered in the left overhead corner of model with coordinates 25÷40 on a horizontal line and on a vertical line (Figure 5). OP in this area gets out equal 0.1.

Figure 5 Evolution of 2D system with heterogeneity through the equal intervals of time.

The evolution of heterogeneity goes in an expected manner. The area of heterogeneity diffuses, broadening in size. Amplitude diminishes here, both due to diffusion and due to relaxation in a volume. The evolution is slowed in the course of time, and the system tends to pass fully to the equilibrium state. For modeling of accidental fluctuations the function of sources n(φ) in (31) chooses in a form of white noise with amplitude 0.1, setting accidentally in every cell. The example of the system evolution is resulted in Figure 6. We see that fluctuations in the initial state have branching fractal-like structure, (the first frame in Figure 6). On later stages of evolution they are localized hearth-like areas (the second frame in Figure 6), which becomes less and less in number, and they diminish in size (the third frame in Figure 6). Finally, they disappear practically from the visible field (the last frame in Figure 6).the chosen relationship between intensity of production of fluctuations and their annihilation, the last prevails. At other parameters other situation is possible. The variant of the second order phase transition reported in this section is comfortable for generalization in the nonequilibrium evolution thermodynamics approaches for description of defect evolution under severe external mechanical load,^13–17 regularities in stick-slip phenomenon in lubricant of different nature^18–21 and so on. Unfortunately, a transition through the critical point T_c did not give the effect of growing of fluctuations; therefore investigation of this case will be executed in the next section, in which the theory of PT-2 is presented in terms of the configurational entropy.

Figure 6 Evolution of 2D system with heterogeneity through the equal intervals of time.

Relation (3) shows a potential possibility for formulation of theory of phase transitions without resorting to the concept of order parameter, but being based directly on (configurational) entropy. It is here necessary to rewrite the base relation (3) in a form

$\varphi =\mp s\sqrt{-\frac{2T_c}{\alpha }}$   (32)

Because of that, a sign of expression under a root is minus, entropy can be either a negative value that corresponds partial or complete ordering or identical zero that corresponds the complete disordering. The free energy (2) in absence of an external field must be written down in a form

$f_s=f_0-2\left(-\left(T-T_c\right)s+2b{\left(\frac{T_c}{\alpha }\right)}^2{s}^2\right)$  at $T<T_c$ , $f_s=f_0$  at $T>T_c$ .  (33)

In this formulation, however, the free energy cannot be presented by unified expression for all of temperature interval, but it is presented as a locally determined function. It is related to that fact that the configurational entropy peaks at the temperature of T=T_c, and at further growth of temperature it remains at this (zero) value. The equilibrium values are determined from a condition

$\frac{\partial f}{\partial s}=2\left(-\left(T-T_c\right)+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s\right)=0$   at $T<T_c$ , $\frac{\partial f}{\partial s}\equiv 0$    at $T>T_c$ .  (34)

From where

$s_1=\frac{1}{2b}\left(T-T_c\right){\left(\frac{\alpha }{T_c}\right)}^2$  at $T<T_c$ , $s_2=0$  at $T>T_c$ .  (35)

At T>T_c the system is in a state of indifferent equilibrium. Any constant s formally satisfies the condition, however, from considering of continuity of the free energy and its first derivatives it follows to choose the second equilibrium value as zero. In principle, it is necessary to write separately Landau – Khalatnikov-like evolution equations for every temperature interval. For the interval T<T_c the type of equation is quite obvious

$\frac{\partial s}{\partial t}=2{\gamma }_1\left(-\left(T-T_c\right)+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s\right)$   (36)

For the interval T>T_c situation is more difficult. Here the system is in the equilibrium state with a maximal chaos. Deviation from this equilibrium state can be only by fluctuation toward diminishing of chaos and appearance of partial ordering. This effect can be only small of the second order with respect to entropy and expansion of the free energy is begun with the quadratic term on entropy. Therefore we will specify the second equation (33)

$f\left(s\right)=f_0+2b{\left(\frac{T_c}{\alpha }\right)}^2{s}^2$   (37)

A coefficient is chosen from those considering, that relief of the free energy must be continuously changed during transition of the critical point. The first Eq. 33 and Eq. 37 can be written as unified equation, if we use theta-function

$f\left(s\right)=f_0-\theta \left(T_c-T\right)\left(T-T_c\right)s+2b{\left(\frac{T_c}{\alpha }\right)}^2{s}^2$   (38)

The curve of the free energy is resulted in Figure 7. From picture evidently that with growth of temperature a minimum of the free energy is uniformly displaced to the right, reaching in the critical point T=T_c=300K of a zero value, and relief of the free energy does not change whereupon. With taking in account Eq. 37 evolution equation is for the case T>T_c looks like

$\frac{\partial s}{\partial t}={\gamma }_1\frac{\partial f}{\partial s}=-4{\gamma }_{1}b{\left(\frac{T_c}{\alpha }\right)}^{2}s$ ,  (39)

$\frac{\partial s}{\partial t}=-2{\gamma }_1\left(\theta \left(T_c-T\right)\left(T-T_c\right)+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s\right)$ .  (40)

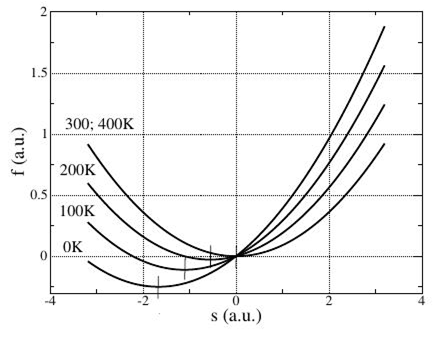
Figure 7 Dependence of the free energy on the entropy and with use of theta-function both Eq. 36 and Eq. 39 can be also written as one equation for all temperature interval.

It is of interest to look, to what Landau – Khalatnikov equation (19) transits at formulation of the problem in terms of the configurational entropy

$\frac{\partial s}{\partial t}=-{\gamma }_f\frac{\partial f}{\partial s}{\left(\frac{\partial s}{\partial \varphi }\right)}^2$ ,  (41)

or with taking in account (32) and explicit expression for the free energy (33) and (37)

$\frac{\partial s}{\partial t}=-2{\gamma }_f\frac{\alpha }{T_c}s\left(T-T_c-2b{\left(\frac{T_c}{\alpha }\right)}^{2}s\right)$  at $T<T_c$ , $\frac{\partial s}{\partial t}=-4{\gamma }_{f}b{\left(\frac{T_c}{\alpha }\right)}^2{s}^2$  at $T>T_c$ .   (42)

The first evolution equation in a form (42) absorbs seemingly in itself both evolution equations (36) and (39) and thus it can be extended in hole temperature interval. Indeed, the multiplier s causes the system to tend to the same steady-state as Eq. 39, and multiplier in parentheses to the same steady-state for Eq. 36. But it is pure outward coincidence, because the multiplier s arose up in this equation as a formal transformation of variables with Jacobean ∂s/∂φ in (40), and it does not any relation to physics of process. The second Eq. 41, which is deprived every sense, testifies about it too, because any negative fluctuation of the entropy causes its further decrease to −∞. Therefore it is most correct to use Eq. 40 for analysis of evolution of a system in terms of the configurational entropy. It does not result by means of limiting transition from the classic Landau – Khalatnikov equation (19) in terms of OP. Taking into account that the configurational entropy is more fundamental quantity as compared to OP, it is necessary to give a preference for it. It is possible to suppose that an attempt to write down the general evolution equation (19) with help of OP at once for a temperature higher and below of critical point contains a latent defect, which, though does not influence on the asymptotic states of the system, but can distort speed kinetics of phase transition. In accordance with (18) and (3) at the absolute zero of temperature the configurational entropy is minimal and negative. It contradicts to the Nernst theorem, in obedience to which entropy at the zero of temperatures must be equal to the zero. For the removal of this contradiction it is enough to shift a scale on entropy,

$s^{\prime }=s+\frac{{\alpha }^2}{2b{T}_c}$   (43)

that at zero temperature the configurational entropy is wittingly equal zero. Then the free energy is look like

$f\left(s\right)=f_0+\frac{{\alpha }^2}{2b{T}_c}\theta \left(T-T_c\right)\left(T-T_c\right)+\frac{{\alpha }^2}{4b}-\theta \left(T_c-T\right)\left(T-T_c\right)s^{\prime }+2b{\left(\frac{T_c}{\alpha }\right)}^2{s^{\prime }}^2$   (44)

At a zero temperature a zero value of the entropy corresponds to a minimum of the free energy, that is, in accordance with the Nernst theorem (Figure 8). With growth of the temperature the entropy grows evenly and takes the maximal value in the critical point T=T_c=300K. Further with growth of the temperature a relief of the free energy does not change, the system reaches a maximal structural disorder, and entropy remains at the attained maximal value. The negative values of configurational entropy are throw-away as unphysical. A minimum value of the free energy grows with growth of the temperature, as well as in case of Figure 7.

Figure 8 Dependence of the free energy on the entropy with satisfaction of Nernst theorem.

Evolution equation (40) for this case is looked like

$\frac{\partial s}{\partial t}=-2{\gamma }_f\left[T_c-\theta \left(T_c-T\right)\left(T-T_c\right)+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s\right]$   (45)

It presents a considerable methodological interest to present the same theory simultaneously in terms of internal energy and configurational entropy. In accordance with (5) and (44) the expressions for the internal energy and its derivatives in this case will look like this

$u\left(s\right)=f_0^{*}-\theta \left(T-T_c\right)\left(T-T_c\right)s+2b{\left(\frac{T_c}{\alpha }\right)}^2{s}^2$ ,  (46)

$T_{rv}=u^{\prime }\left(s\right)=-\theta \left(T-T_c\right)\left(T-T_c\right)+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s$ ,  (47)

$u^{″}\left(s\right)=2b{\left(\frac{T_c}{\alpha }\right)}^2$ ,  (48)

where

$f_0^{*}=f_0+\frac{{\alpha }^2}{2b{T}_c}\theta \left(T_c-T\right)\left(T-T_c\right)+\frac{{\alpha }^2}{4b}$ ,  (49)

where the dash of variable s is dropped. Here T_rv is a current value of the temperature, which in the equilibrium state coincides with T, that, with the temperature of external thermostat. The curves of the internal energy and current temperature are resulted in Figure 9. With the increase of temperature up to critical a minimum of the internal energy grows all of time, remaining at a zero value of the configurational entropy. Here the curves of current temperature coincide between itself for all temperatures (line 1). Their equilibrium values at different temperatures however differ between itself and equal to the temperature of external thermostat. Compare vertical lines in Figure 9, drawn between the abscissas axis and the straight line of current temperature in the equilibrium states for temperatures 100, 200 and 300K. At a zero temperature of thermostat the equilibrium value of current temperature is equal to the zero.

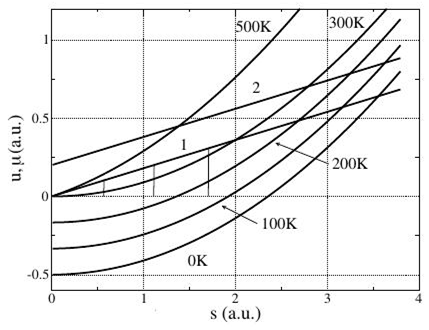
Figure 9 Dependence of the internal energy and its derivatives on the entropy.

At temperatures higher critical ones the minimum of the internal energy moves in the negative unphysical area of configurational entropy values. The curve of current temperature with growth of temperature of thermostat begins to be evenly moved upwards along the abscise axis. The equilibrium value of current temperature accordingly grows also. Let us evident that the equilibrium value of current temperature coincides with the temperature of thermostat. We define the equilibrium value of the configurational entropy from an obvious condition

$\frac{\partial f}{\partial s}=-\theta \left(T_c-T\right)\left(T-T_c\right)-T_c+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s=0$ ,  (50)

from where follows

$s_{eq}=\frac{1}{2b}{\left(\frac{\alpha }{T_c}\right)}^2\left[\theta \left(T_c-T\right)\left(T-T_c\right)+T_c\right]$   (51)

Substituting this value in (47) we get

$T_{rv}=\theta \left(T-T_c\right)\left(T-T_c\right)+\theta \left(T_c-T\right)\left(T-T_c\right)+T_c\equiv T$   (52)

The analogue of the evolution equation (20) in terms of entropy then has more natural form

$\frac{\partial f}{\partial s}={\gamma }_s\left(\frac{\partial u}{\partial s}-T\right)$   (53)

that, the system is evoluated until a current temperature is accepted the temperature of thermostat. For a heterogeneous problem equation (31) in terms of configurational entropy it is possible to write down in a form

$\frac{\partial s}{\partial t}={\gamma }_s\left(-c\Delta s+2b{\left(\frac{T_c}{\alpha }\right)}^{2}s\right)+n\left(s\right)$   (54)

We put this equation in basis for calculation of fluctuations, arising up at passing of critical temperature of the system (Figure 10). The primary temperature of thermostat got out equal a bit higher critical T=300.1K, and goes down slowly. In the vicinity of critical temperature, predictably, there are intensive long-living fluctuations. It is interest that in the strictly critical point long-living fluctuations dies out, and general level of fluctuations go down to the thermal background. It is related to that distinction between two types of steady-states in a critical point disappears, and they cannot serve more by the traps of thermal fluctuations for each other. Therefore excrescence of fluctuations takes a place not strictly in a critical point, but in some vicinity of it. Thus, in this paper a theory of the second order phase transitions is considered from four different positions – in terms of free and internal energy in language of order parameter, and also in language of configurational entropy. The indicated variants cannot simply be taken to each other, and formulation in language of configurational entropy seems more preferable. Evolution equation in terms of the internal energy in language of configurational entropy has clear physical sense, meaning tendency of current temperature of the system to the temperature of external thermostat. The analysis of long-living fluctuations, arising up in the vicinity of critical temperature due to transitions between two types of the states, shows that in the strictly critical point the level of fluctuations goes down to the average thermal background.

Figure 10 Dependence of the internal energy and its derivatives on the entropy.

In this paper a theory of the second order phase transitions is considered from four different positions in terms of free and internal energy in language of order parameter, and also in language of configurational entropy. The indicated variants cannot simply be taken to each other, and formulation in language of configurational entropy seems more preferable. Evolution equation in terms of the internal energy in language of configurational entropy has clear physical sense, meaning tendency of current temperature of the system to the temperature of external thermostat. The analysis of long-living fluctuations, arising up in the vicinity of critical temperature due to transitions between two types of the states, shows that in the strictly critical point the level of fluctuations goes down to the average thermal background. We mark that theory of PT-2, developed here in terms of entropy, can enough correctly describe order - disorder phase transition at transition of Curie point, for example, in a magnetic. Thus heterogeneous terms in the free and internal energy describe generation and disappearing of accidental structural fluctuations. At the same time, within the framework of this theory it is while problematic to describe structural heterogeneity of the second type, namely origin of regular antiphase boundaries.²² For solution of this problem a complication of the model is required by introduction of additional degree of disorder.

None.

The author declares there is no conflict of interest.

1. Landau LD, Phys Z Sowjetunion On the theory of phase changes II . 1937.
2. On the Theory of Phase Transitions. Phys Z Sowjet. 1937;11:545.
3. Aranson IS, Kalatsky VA, Vinocur VM. Continuum Field Description of Crack Propagation. Phys. Rev. Lett. 2000;85:118.
4. Eastgate LO, Sethna JP, Rauscher M, et al. Fracture in Mode I using a Conserved Phase-Field. Model Physc Rev. 2002;65:036117.
5. Levitas VI, Preston DL, Lee DW. Three-dimensional Landau theory for multivariant stress-induced martensitic phase transformations. II. Multivariant phase transformations and stress space analysis.  Phys Rev B.  2003;68:134201.
6. J. C. Ramirez, C. Beckermann, Karma A, et al. Phase-field modeling of binary alloy solidification with coupled heat and solute diffusion. Phys Rev E. 2004;69:051607.
7. Granasy L, Pusztai T, Tegze G, et al. Phase field theory of crystal nucleation and polycrystalline growth: A review. Phys Rev E. 2005;72:011605.
8. Achim CV, Karttunen M, Elder KR, et al. Phase diagram and commensurate-incommensurate transitions in the phase field crystal
9. model with an external pinning potential. Phys Rev E. 2006;74:0211044.
10. Svandal A. Modeling hydrate phase transitions using mean-field approaches. 2006.
11. Rosam J, Jimack PK, Mullis AM. Quantitative phase-field modeling of solidification at high Lewis number. Phys Rev E. 2009;79:030601.
12. J. Choudhury, and B. Nestler. Grand-potential formulation for multicomponent phase transformations combined with thin-interface asymptotics of the double-obstacle potential. Phys Rev E. 2012;85:021602.
13. Patashinsky AZ, Pokrovsky VL. Fluctuation Theory of Phase Transitions. 1979.
14. Metlov LS. Nonequilibrium Evolution Thermodynamics of Vacancies. Phys Rev Lett. 2011;106:165506.
15. LS Metlov. Tribological properties of dry, fluid, and boundary friction. Phys Rev E. 2010;81:051121.
16. LS Metlov. Nonequilibrium dynamics of a two-defect system under severe load. Phys Rev E. 2014;90:022124.
17. A Khomenko, D Troshchenko, L Metlov. Effect of stochastic processes on structure formation in nanocrystalline materials under severe plastic deformation. Phys Rev E. 2019;100:022110.
18. LS Metlov. High Press. Phys Technics. 2019;29:1–28.
19. IA Lyashenko, AV Khomenko, LS Metlov. Tribology International. 2011;44:486.
20. AV Khomenko, OV Yushchenko. Solid-liquid transition of ultrathin lubricant film. Phys Rev E. 2013;68:036110.
21. AV Khomenko, IA Lyashenko. Phys Lett A. 2007;366:1-2:165.
22. AV Khomenko, IA Lyashenko. Effect of the temperature dependence of the viscosity of pseudoplastic lubricants on the boundary friction regime. J Frict Wear. 2010;31:4–308.
23. IB Krasnuk, TN Melnik, VM Yurchenko. Scientific records of Tavriya national university. 2012;25(64):1–193.