This paper presents a novel analysis of galaxy formation through the lens of the Small Bang Model, which posits the existence of two distinct types of galaxies generated by micro black holes: matter galaxies generated by antimatter supermassive black holes (SMBHs) and antimatter galaxies generated by matter SMBHs. The relationship between the mass of galaxies and their respective SMBHs is explored, leading to the derivation of two specific mass ratios: 918 for matter galaxies and 324 for antimatter galaxies. By using a dataset of 100 galaxies from a reliable source, the research identifies two separate subsets of galaxies with low measurement error, totaling 41 galaxies. Among these, 31 galaxies (77%) are identified as matter galaxies with a mass ratio of 918, while 10 galaxies (23%) are classified as antimatter galaxies with a mass ratio of 324. The analysis reveals that, despite measurement noise, the data aligns closely with the theoretical predictions for these two distinct types of galaxies.

The research provides a strong indication that galaxies and their SMBHs are governed by fixed mass relationships, challenging the idea that these relationships are random or nonlinear. This supports the Small Bang Model, which offers a compelling alternative to the Big Bang Model, with no initial singularity and a universe emerging from a low-energy state. The findings suggest that this model not only explains the formation of spiral galaxies but also accounts for the origin of supermassive black holes at the center of each galaxy. Further study is encouraged, as this discovery opens new avenues for understanding the role of antimatter in the universe and the formation of galaxies.

Galaxies are the largest objects observed in our universe. Composed of billions of stars, they form relatively isolated "islands." At the center of each galaxy, there is typically a supermassive black hole (SMBH) with a mass equivalent to millions of stars. While a relationship between the masses of galaxies and their SMBHs is often observed, extreme cases show the mass of a galaxy being between 50 and 7,000 times greater than the mass of the SMBH.

The authors of this article are developing a new cosmological model called the Small Bang Model (SBM),^1-3 which proposes a universe that begins cold, empty, and devoid of matter or energy. In the SBM, the mass of all galaxies we observe today is created through the interaction of micro black holes with the cosmic inflation field. The inflaton field forces the micro black hole (whether of matter or antimatter) to grow. For example, a micro black hole (μBH) of antimatter grows by consuming antiprotons and positrons from the vacuum and expelling protons and electrons, which form a hydrogen cloud shaped like a spiral disk. By the end of cosmic inflation, the mass of the μBH increases by a factor of 10⁵⁰, transforming into a SMBH surrounded by a hydrogen cloud hundreds of light-years in diameter. Given that the number of antiparticles consumed by the μBH of antimatter equals the number of particles expelled to form the cloud, one might expect the SMBH's mass to equal the mass of its host galaxy.

However, the authors developed a theory called UT^4,5 (Ulianov Theory) within which a new space-time context^6,7 was defined and a new string theory the UST^8,9 ( Ulianov String Theory) proposes that electrons and protons10 are composed of the same type of string, differing only in the way they coil. Furthermore, the particle's mass is proportional to the number of coils.

According to UST, protons (and antiprotons) coil into dense, 3D spheres with many coils, leading to a large mass. Electrons (and positrons), on the other hand, coil into 2D spherical shells with fewer coils, resulting in a mass 1,836 times smaller than that of a proton.¹¹ In this model, when an antiproton falls into an antimatter black hole, it loses its 3D coil and transforms into a 2D coil, reducing its mass to that of a positron.¹⁰

Thus, the mass of particles falling into an antimatter black hole (or μBH) is greatly reduced,⁵ as the antiproton's mass decreases by a factor of 1,836. This explains why the ratio of the mass of a galaxy to the mass of its SMBH is not 1:1 but rather defined by:

$\frac{M_{Galaxy}}{M_{SMBH}}=\frac{1}{2}\left(\frac{M_{Proton}}{M_{Electron}}+1\right)=918.58$

$\text{lo}{g}_{10}\left(\frac{M_{Galaxy}}{M_{SMBH}}\right)=2.963$   (1)

Similarly, the UST proposes that black holes composed of matter are nearly three times heavier than black holes composed of antimatter. This implies that, in the case of an antimatter galaxy, the ratio of its mass to the mass of the supermassive black hole of matter at its center would follow the same relationship.

$\frac{M_{Galaxy}}{M_{SMBH}}=\frac{1}{4\sqrt{\left(2\right)}}\left(\frac{M_{Proton}}{M_{Electron}}+1\right)=324.77$

$\text{lo}{g}_{10}\left(\frac{M_{Galaxy}}{M_{SMBH}}\right)=2.512$   (2)

To validate this theory, we utilized a table obtained from a previous paper,¹² which includes a sample of 100 representative SMBHs selected based on X-ray-selected active galactic nuclei (AGNs) within the Chandra-COSMOS Legacy Survey. This table includes several columns, such as object ID, redshift, logarithm of SMBH mass, logarithm of AGN bolometric luminosity, logarithm of galaxy mass, the instrument used for spectroscopy, and the specific broad emission line employed.

However, when we plotted these available data on two graphs, as shown in Figure 1, an almost random mass ratio (from 1.54 to 3.85) presented that significantly deviated from the value (2.963) predicted by Equation 1.

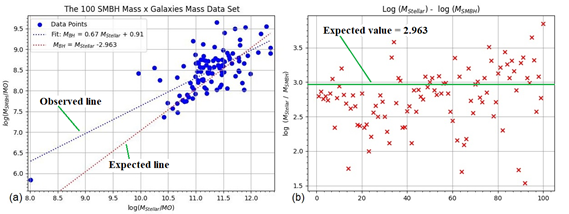
Figure 1 a) Graph with 100 available mass relation points, with the horizontal axis representing the galaxy mass value of $Lo{g}_{10}$ galaxy mass (divided by the Sun's mass) and the vertical axis representing the SMBH mass value of $Lo{g}_{10}$ SMBH mass (divided by the Sun's mass). The theoretical line, defined by Equation (1), is shown in red dots (Expected line), and the interpolated line is shown in black dots (Observed line). b) Graph showing the $Lo{g}_{10}$  relation between the galaxy mass and the SMBH mass (logarithm of galaxy mass divided by SMBH mass), where the expected value (2.963) is presented as a green line.

However, upon closer inspection of the available data, it was found that there is an associated error value in the measurement of the SMBH masses, as well as two error values associated with the measurement of the galaxy masses (set of three values for the two type of mass). Based on these three error values, it was possible to determine a total mean square error for each point. In some cases, the errors in the table were equal to zero, which was considered inconsistent, and a minimum acceptable error of 0.05 (logarithmic value) was defined (replacing the errors smaller than 0.05).

The available points were organized in ascending order of total error and divided into five error ranges, as shown in Table 1. For example, points with an error between 0.20 and 0.35 are located between positions 41 and 66, totaling 25 points within this error range. The percentage variation column shows what this logarithmic error means in terms of absolute values. For instance, in the last row of the table, we observe errors in the range of 0.7 to 1.45, with an average percentage variation from -91.7% to 1102.3%. This means that if a mass ratio is measured as 1,000, within this error range it could vary from 83 (losing 91.7% of 1,000) to 12,023 (gaining 1102.3% of 1,000).

Given this large variation, it becomes evident that for the 8 points in this highest error range, if a ratio of 500 is observed, this could be 10 times smaller or 10 times larger, varying from 50 to 5,000. Thus, the question arises: What is the use of a mass ratio between a galaxy and its SMBH that could range from 50 to 5,000? For example, consider the largest ratio in the available database: galaxy Lid_3456 has a mass of  ${10}^{11.87}{M}_{Sun}$ , and its supermassive black hole has a mass of ${10}^{8.02}{M}_{Sun}$ , resulting in a ratio of ${10}^{3.850}$ = 7,077. However, the total error in this case is 0.54, leading to a variation between 1,893 and 26,463. This raises a new question: Can we truly consider a maximum mass ratio of 7,077 in a case where, due to high error, the ratio could vary between 1.8 thousand and 26 thousand?

Thus, our initial consideration was that even the third range in Table 1, which spans from 0.35 to 0.5 (for a mean value of 1,000, this error range generates a variation from 385 to 2,600), represents a very high error. Consequently, we made a selection of only 66 points with an error of less than 0.35 (corresponding to a variation from 575 to 1,738 for a measured value of 1,000). Upon this selection, we observed two distinct sets of relations between galaxy mass and SMBH mass: one set with values near 2.9 and another near 2.4. As these values closely match the theoretical predictions presented in Equations (1) and (2), which predict logarithmic relations of 2.94 for matter galaxies and 2.51 for antimatter galaxies, we divided the dataset into two groups of points. These groups are shown in Figure 2. In the graphs, we observed that the curves generated through interpolation closely follow the theoretical curves.

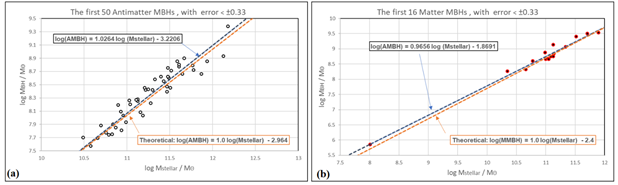
Figure 2 a) Logarithmic plot of the mass of 50 antimatter SMBHs versus the mass of their respective host galaxies. Only points with a total mean square error of less than +/- 0.35 are included. b) Logarithmic plot of the mass of 16 matter SMBHs versus the mass of their respective host galaxies. Only points with a total mean square error of less than +/- 0.35 are included.

At this stage of the work, a disagreement arose between the authors. Jonas Negreiros argued that removing 44 points from the existing dataset could be considered biased, especially since extreme points (where mass ratios were above 2,500 and below 150) ended up being excluded. On the other hand, Policarpo Ulianov contended that errors ranging from 0.20 to 0.35—representing up to three times the variation (with values ranging from 575 to 1,738 when the measured value is 1,000 and from 191 to 597 when the measured value is 333)—still constituted significant errors, especially when distinguishing between the two distinct ratios of 2.51 and 2.96. For instance, a mass ratio of 580 could either represent a true ratio of 1,000 with a negative error or a ratio of 333 with a positive error.

Dr. Ulianov proposed retaining only the 41 most reliable points (presented in Table 2 and Table 3) with errors between 0.05 and 0.20, as these provide acceptable variation within a range of 1.6 times: from 777 to 1,288 when the measured value is 1,000, and from 259 to 429 when the measured value is 333. This allows for a clear distinction between the two ratios, as there remains a significant range (from 429 to 777) separating the two theoretical values, even for points with maximum errors. Therefore, Dr. Ulianov suggested excluding 59 points with medium and larger errors (ranging from 0.20 to 1.45), as they introduced too much uncertainty and could obscure the clear separation between the two ratios.

Analogy of the three targets

This analogy involves an experiment using three targets, with radii of 30 cm, 28 cm, and 25 cm, respectively. One hundred professional and amateur dart throwers are gathered, and each of them will throw several darts towards the targets across four different experiments. The setup consists of a wall measuring 1.5 meters in width and height, equipped with a set of sensors that can determine the position where each dart hits the wall, with a resolution of 1 mm. The three targets are drawn on thin paper and can be fixed to the wall, one at a time, in any position. When a player throws a dart, two pieces of information are recorded for each throw: the XY position where the dart hits and the  XY (top edge point) position of the target.

The experiment is conducted in four stages:

Step 1 - Preparation: The 30 cm radius target is fixed at the center of the wall. Each player throws 100 darts at this target (trying to hit the center of the target), and the distance from the point where the dart hits to the center of the target is measured in centimeters. From the 100 throws, the five largest distances are discarded, and the largest of the 95 distances remainder, defines the player's accuracy, with a resolution of 0.5 cm. After this step, it was found that 41 players had an accuracy between 0.5 and 2.0 cm, 25 players had an accuracy between 2.0 and 3.5 cm, 15 players had an accuracy between 3.5 and 5.0 cm, 11 players had an accuracy between 5.0 and 7.0 cm, and 8 players had an accuracy between 7.0 and 14.5 cm. It is important to note that in 95% of their throws, the players achieved a distance below this accuracy value, and therefore in a new throw, it is expected with 95% confidence that the distance will also be below this maximum precision value.

Step 2 - Experiment A: A diagonal line is drawn from the point (0,0) cm to the point (150,150) cm. The 28 cm target is randomly positioned along this line (with the top of the target touching the line) within the x-coordinate range of 70 cm to 130 cm. For each target position, a player throws a single dart (trying to hit the center of the target), and two pieces of information are collected: the distance between the dart (hit point) to the target top edge (point where the target edge touch the line) and the XY position where the dart hit the wall.

Step 3 - Experiment B: The same procedure as in Experiment A is followed, but this time two targets are used: one with a radius of 30 cm (presented 70 times) and the other with a radius of 25 cm (presented 30 times). Each player throws only one dart at a randomly assigned target, resulting in 100 sets of values.

Step 4 - Experiment C: The same procedure as in Experiment A is followed, but now 100 targets of random sizes (with radii ranging from 5 cm to 50 cm) are used. Each player throws a single dart at a different target, generating 100 sets of values.

To better understand this experiment, let us first consider 100 perfect players with an accuracy of 0.5 cm (-0.5 to +0.5 cm of deviation from the target central point, resulting in a 1 cm range) participating in Experiments A, B, and C.

As shown in Figure 2, the distances from the target top edge to the dart position will vary between 27.4 and 28.5 cm in Experiment A, since the players are essentially hitting the center of the target with an error margin of ±0.5 cm. In Experiment B, two sets of distances will be observed: the first set of 70 samples will vary from 29.5 to 30.5 cm, and the second set of 30 samples will vary from 24.5 to 25.5 cm. In Experiment C, with 100 targets of different random sizes, the dart distances to the target top edge will vary randomly between 4.5 cm and 50.5 cm (Figure 3 & 4).

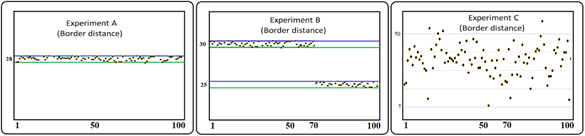
Figure 3 Results for the target border distance measurement performed by 100 perfect players (precision of 0.5 cm) in experiments A (28 cm radius target), B (70 throws with a 30 cm radius target and 30 throws with a 25 cm radius target), and C (100 targets with radii ranging from 5 to 50 cm).

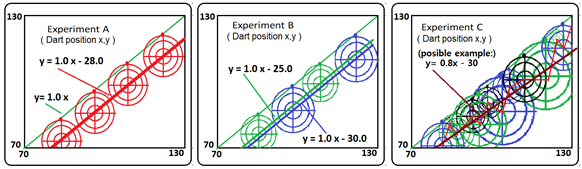
Figure 4 Results for the dart XY position measurement performed by 100 perfect players (precision of 0.5cm) in experiments A (28 cm radius target), B (70 throws with a 30 cm radius target and 30 throws with a 25 cm radius target), and C (100 targets with radii ranging from 5 to 50 cm).

Figure 3 presents the results of three experiments performed by 100 perfect players. In Experiment A, the XY dart position points (that is equal to the target center ±0.5, for perfect players) align along a well-defined line given by the equation , easily obtained through linear interpolation. In Experiment B, two linear equations emerge: and , which can also be derived through interpolation by separating the data into two sets. In Experiment C, the points form an ascending, yet random, path. Applying linear interpolation here will yield a positive slope, but the gain factor (a) may deviate larger from 1.0, and the offset (b) could be either positive or negative.

In the end of these three experiments, three datasets are generated. Each dataset has 100 points containing four values: the distance between the dart and the target top edge (in cm), the dart's X and Y wall hit positions (in cm), and the player's precision (ranging from 0.5 to 14.5 cm). The player's precision defines the expected maximum distance between the dart and the target center with 95% certainty that the actual distance will be below this value.

Three teams of metrology experts analyze the datasets without knowing which experiment the data came from. Their task is to determine whether the data corresponds to Experiment A, B, or C. Interestingly, the analysis does not require astronomers or physicists, but rather a keen understanding of how each player's precision affects the results, a task suitable for metrologists. Dr. Ulianov, whose expertise is in metrology, designed this experiment to emphasize the role of measurement uncertainty in identifying patterns within the data.

The first observation is that if the measurements were perfectly accurate, the resulting curves would be straight lines, making it easy to distinguish data from Experiments A, B, and C. However, due to factors affecting dart throws, players produce measurements with varying degrees of error, which can be modeled and predicted. In measurement systems, this reflects the fact that errors will always exist, and they define an uncertainty range, typically modeled as a normal distribution. In this experiment, a 95% confidence level (2 sigma) was used to ensure that errors remain within the player's precision range. However, distinguishing between targets with similar radii (30 cm, 28 cm, and 25 cm) becomes challenging.

Note that we need only a few perfect players (for example only 10 players with 0.5 cm precision), that are enough to determine with experiment generated the available data. For example, in the dart to target (top edge ) distance value, in the case of experiment A, we will see 10 values near 28 cm and the case B will produce two sets of values (near 25 cm and near 30 cm) and case C will produce 10 random values (from 5 to 50cm). Otherwise, players with low precision generate data that is essentially noise, and their measurements can be discarded. For example, players with precision between 5.0 and 14.5 cm contribute with little useful data, and those with precision between 3.0 and 5.0 cm not allows to distinguish the targets small distances. This raises the main question of whether to use only the “professional players” (41 data points with players precision between 0.5 and 2.0 cm) or also include the “medium players” 25 data points (with precision between 2.0 and 3.0 cm).

While it seems advantageous to use 66 values, the 4 cm to 6 cm variation (from players precision in 2 cm to 3 cm range) becomes problematic, as it exceeds the 2 cm difference between targets (between 28cm and 30 cm radius targets). In contrast, using only 41 the most precise measurements from “professional players” allows us to clearly separate Experiments A and B and C (probably the data from just 10 perfect players would already be enough to do this so 41 points from “professional players” is still a very large number to choosing in the three cases scenario).

In Experiment A, where there is only one target, the measurements fall within a defined range depending on the player's precision. The challenge in Experiment B arises from the possibility that all precise players might have thrown at the 30 cm target, missing the 25 cm target altogether. However, this is statistically unlikely due to the random distribution of target sizes among players. Based on probability, it's expected that 28 of the 41 best players will have used the 30 cm target and 12 will have used the 25 cm target, resulting in distinct measurement ranges for each target size.

To confirm these observations, linear interpolation of the XY data can be used to differentiate between the two target sizes in Experiment B. Although the interpolated line may not have a perfect slope of 1.000, small deviations in the gain factor can help identify whether the data corresponds to Experiment A or B. In this way, the error in the linear interpolation serves as a key indicator for distinguishing between the two experiments. Since three straight lines will be obtained, three gain coefficients will be available for analysis. In the case of Experiment A, one coefficient (using the entire data set for interpolation) will be close to 1.000, while the other two coefficients will deviate further from 1.000. However, in the case of Experiment B, two gain coefficients (obtained by dividing the data set into two groups) will be close to 1.000, and the third coefficient (considering the entire data set as a single group) will deviate more significantly from 1.000.

Using the three targets analogy conclusions

We can see that the analogy of the three targets is directly connected to the problem of measuring the logarithmic relationship between the mass of a galaxy and the mass of its supermassive black hole (SMBH). The only difference is that, instead of a target with a radius of 30 cm, we have a mass ratio of 2.96; instead of a target with a radius of 25 cm, we have a mass ratio of 2.51; and the target of 28 cm is linked to an average value of 2.80. Additionally, the precision range of 0.5 cm to 2.0 cm is analogous to the total measurement error of 0.05 to 0.20 logarithmic values. It should be noted that there are two basic types of errors in the available dataset: one associated with the measurement of the SMBH mass and another with the measurement of the galaxy mass. In some cases, errors were reported as zero (which is a metrological inconsistency), and in others, the reported errors were very small (e.g., 0.01 or 0.02), which is unrealistic given that the data involves similar measurements that should have comparable uncertainties, with average errors around 0.25 and maximum errors reaching up to 1.5.

To address this, the smallest individual errors were rounded into three ranges: 0.05, 0.10, and 0.15. For instance, an error originally recorded in the range of 0.00 to 0.04 was rounded to 0.05 to maintain consistency across the dataset.

Tables 1 and 2 present 41 data points of galaxy masses and SMBH masses, selected from a total of 100 available points due to their low associated error (less than or equal to 0.15 for mass measure errors and less or equal to than 0.21 for total errors).

The dataset was obtained from a research paper,¹² which indicates that these mass values represent significant samples of the mass distributions of galaxies and supermassive black holes throughout the universe. When compared with the original table, the mass values in tables 2 and 3 remain the same, but the errors have been rounded. Additionally, in the case of galaxy mass errors, there were originally two error values (one positive and one negative), which were averaged by summing them and dividing by two. Observing Figures 5 and 6 and comparing them with the graphs in Figure 3 (which show an analogy with the target experiments), it is clear that this corresponds to Experiment B, where two types of targets (30 cm and 25 cm) are being used. This means that Experiment C, which considers targets with random radii, can be completely discarded. In the context of the analogous problem regarding the relationship between the masses of galaxies and their supermassive black holes (SMBHs), Figure 5 clearly shows that there are two types of relationships (one with an average of 2.9 and the other with an average of 2.4).

This indicates that there are indeed two groups of galaxies in the universe generating the measured data. Looking again at the graph in Figure 1-b, it may appear that the relationship between galaxy mass and SMBH mass is random (as in Experiment C), but if the relationships were truly random, this pattern would be seen in both the 41-point set and the 100-point set. It is impossible for a random set to become non-random simply by dividing it in half (Table 3) (Figure 5 & 6).

Figure 5 Graph obtained from Tables 3 and 4: Relation with total error added (LIM SUP in blue) and total error subtracted (LIM INF in green), with theoretical values (2.96 and 2.51) shown in red.

Figure 6 Graph obtained by merging Tables 3 and 4 into a single set of galaxies, obtaining 41 relations. The theoretical value of 2.80 is only a mean value, with no theoretical equation to deduce this value.

In Table 3, the last line present the errors 0.05 in red because all three errors (in the original table) are equal zero meaning a high accurate measurement (it was changed to 0.05 by the authors, to use a more realistic value) or more likely that in this case the error was note calculated being informed as zero. The fact is that the measured values do not form straight lines because there are errors associated with each measurement. We can see that if the data is treated as a single group of galaxies (as shown in the graph in Figure 6) with an average relationship value of 2.80 (Experiment A), there will be 9 points (indicated by red circles in the figure) where the measured value falls outside the expected error. This means that modeling the relationships as a single group does not provide a solution compatible with the observed errors values. On the other hand, considering that there are two groups of galaxies with two different mass ratios (relative to the mass of their supermassive black holes), all points in the matter galaxies group fall within the expected error range, with only one point in the antimatter galaxies group falling outside the expected range.

However, when examining this point in the original table, we notice that some points have errors equal to zero, with objects cid_495 (and also cid_1174) being the only two cases in the 100 points data set where all three error values presented in the table are zero. Having an error value of zero is absurd from a metrological perspective, but since all three errors for this point are listed as zero (same of object cid_1174 that also present problem as presented in Figure 9), it could indicate that either it is an exceptionally accurate measurement or, more likely, that the errors were not calculated and the value was filled with zero. If the errors for this point should be in the range of 0.35 to 0.40, and therefore cid_495 should not have been included in this 41 points low errors analysis (the cid_1174 was removed but we left the cid_495 on purpose in Figure 5, to raise this zero-error issue), when in fact it is an unrecognized error, and the method is capable of detecting this. Thus, instead of seeing the red-circled point in Figure 5 as a problem, it actually shows that the method is robust enough to detect a point incorrectly labeled with small error.

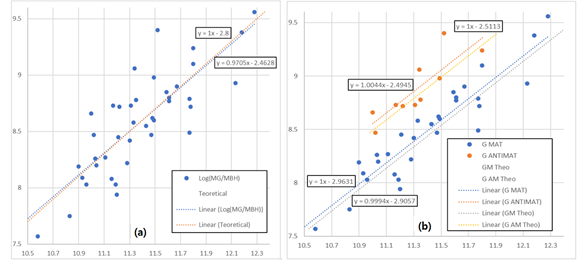
Figure 7 b) Graph of galaxy masses versus SMBH masses considering two data sets obtained from Tables 2 and 3. The theoretical curves can be defined as $log\left(M_{S}MBH\right)=1.0log\left(M_{G}alax\right)-2.963$ and $log\left(M_{S}MBH\right)=1.0log\left(M_{G}alax\right)-2.511$ . The interpolated lines were obtained using the linear fit procedure available in the Excel graph . a) Same graph as (b) but considering only one data set (merging the data from Tables 2 and 3). In this case (related to target experiment A) the theoretical curve can be defined as $log\left(M_{S}MBH\right)=1.0log\left(M_{G}alax\right)-2.800$ .

Figure 7 presents an XY graph similar to the graphs in Figure 3 for Experiment A (Figure 6-a) and Experiment B (Figure 6-b). Looking at the two graphs in Figure 6, graph (a) might appear better because the theoretical value line is closer to the interpolated value line. However, in (a), the theoretical value was obtained from the data itself (as an average relationship value), so the theoretical line is also an interpolated line (with a unitary gain factor). Thus, it is expected that the two lines will closely coincide.

In contrast, in graph (b), the theoretical lines were derived from logical and mathematical deductions. Therefore, it is surprising how close the theoretical lines are to the interpolated lines. A distance of 0.03 to 0.05 can be observed between the theoretical and interpolated lines, but it should be noted that this interval represents the minimum precision error observed in the system. The fact that masses are represented with two digits already generates an uncertainty of ±0.01 for each mass (since a mass of 2.05 could be a rounding of 2.055 or 2.045, leading to a variation between 2.04 and 2.06). Consequently, the average precision in the total error is approximately ±0.015. In other words, simply representing the masses with two decimal places introduces a variation range of 0.03. Thus, we either consider this error negligible, or we should represent the mass values with three decimal places.

However, two more important aspects need to be observed in Figure 6. The first is that, when the data set is divided into two categories, the measurement points exhibit more uniform patterns (with similar errors on both sides) and are closer to each line. When using only one line, the point distribution patterns above and below the line differ slightly, whereas using two lines eliminates this effect, providing further indication that there are indeed two distinct data sets.

The second aspect becomes evident when we observe the gain factors of each interpolated curve, which ideally should be equal to one, because if there is a linear relationship, the logarithmic equation becomes:

Note that for example

$\log \left(M_{SMBH}\right)=1.0\text{log}\left(M_{Galax}\right)-\text{log}\left(K_A\right)$

$\log \left(M_{SMBH}\right)=0.8\text{log}\left(M_{Galax}\right)-\text{log}\left(K_A\right)$ this generates the equation:

$M_{Galax}^{0.8}=K_A{M}_{SMBH}$

Thus, if the gain factor of the interpolated line is significantly different from 1.00, it indicates a non-linear relationship between the mass of the galaxy and the mass of the SMBH, or it could even suggest a random process (or one defined by hidden or unobserved variables). For example, in the analogy of the three targets, Experiment C could be generated by increasing the size of the target as a function of the value of x squared, which would yield a gain factor of 0.5 in the interpolated line. The key point here is that gain factors other than 1.00 imply non-linear relationships; however, a small deviation (within the range of 0.90 to 1.10) is acceptable due to noise in the data.

Observing the interpolated lines in Figure 6, we find the following:

1. For Table 2 data set (matter galaxies):$\log \left(M_{SMBH}\right)=0.9994\log \left(M_{Galax}\right)-2.9057$
2. For Table 3 data set (antimatter galaxies):$\log \left(M_{SMBH}\right)=1.0044\log \left(M_{Galax}\right)-2.4945$
3. Considering a single data set (only matter galaxies in the universe): $\log \left(M_{SMBH}\right)=0.9705\log \left(M_{Galax}\right)-2.4628$

Thus, when considering the data sets separately versus a single unified set, the error in the gain factor for the interpolated line is around 3%. However, when the two sets are considered separately, the error drops to 0.06% for one set and 0.44% for the other.

These error values are so evident that it becomes unnecessary to indicate which theoretical model is superior. Observing Figures 5, 6, and 7, it is clear, with 100% certainty, that the data corresponds to Experiment B, where the use of two targets (one with a radius of 30 cm and another with a radius of 25 cm) generates two distinct sets of data. In the real case of galaxies, this points to the existence of two distinct mass relationships. Moreover, the factors obtained from the interpolated lines (2.9057 and 2.4945) closely match the theoretical values (2.963 and 2.511) predicted by the model. This makes it nearly certain that the larger set (Table 2) corresponds to matter galaxies, while the smaller set (Table 3) corresponds to antimatter galaxies.

It is also worth noting that while the scenario presented by Experiment A (using a single 28 cm target) is theoretically possible, it is highly unlikely. This would imply that in 9 out of 41 cases (21% of the total used points), astronomers miscalculated the error estimates. In contrast, in the scenario of Experiment B, there is only one problematic point (where the astronomers simply did not calculate the error, and all three original errors were incorrectly reported as zero) (Figure 8).

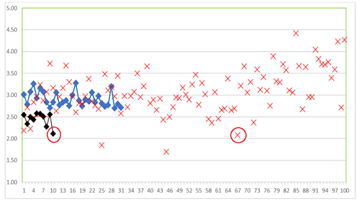
Figure 8 Superposition of graphs from Figures 1 and 5. The red circle indicates a point with a larger calculated error than the theoretical error (point presented in red the Table 2 last line). It also shows that the 41 blue and black points are repeated in the red X marks, which represent the complete data set.

In Figure 8, we can observe the difference between using only 41 points with small errors and the complete data set of 100 points. For the 10 black points (antimatter galaxies), the mass ratio varies from 2.28 to 2.58 (191 to 380). For the 31 blue points (matter galaxies), the mass ratio varies from 2.70 to 3.28 (501 to 1905). For all 100 points, the mass ratio varies from 1.540 to 3.85 (35 to 7077) meaning a 202 times variation. It is important to note that an error of 0.21 (the maximum total error in the total of 41-point data set) results in a 3.0 times variation. An error of 0.7 (found in 19 points of the total data set) results in a 25 times variation, while an error of 1.45 (the maximum total error in the data set) results in a 794 times variation.

So, what happens when we mix points with mass ratios that vary 3 times, with points that vary from 25 to 700 times?

The final variation will be between, 25 and 700 and so a variation of 200 is something expected. Obviously, this means that the variation of 200 comes from the points with the highest error and if they are excluded from the set this drops to the range of 2 to 3 as can be seen in Figure 8 graphs variations.

These variations highlight a stark contrast between reasonable variations, which suggest accurate measurements, and absurd variations, which hold no meaningful significance. This issue is rooted in the lack of proper metrological practices by the astronomers, who have not yet recognized that there is a linear relationship between the mass of galaxies and the mass of supermassive black holes. Furthermore, this analysis reveals that there are, in fact, two types of mass ratios, corresponding to the existence of two types of galaxies and two types of supermassive black holes.   

Global error analise 

If we accept that the mass ratio for antimatter galaxies is indeed 2.51 and for matter galaxies is 2.96, this allows us to calculate a new type of error (the measurement error relative to the theoretical value), which can be compared to the theoretical measurement error predicted by astronomers. This was previously demonstrated in the case of galaxy cid_459, where the observed measurement error (0.35) was significantly larger than the expected theoretical error (0.07). This discrepancy allowed us to identify a problem in the calculation of the theoretical error (which, in this case, was incorrectly listed as zero, indicating an undefined and unknown error). Expanding this concept to all 100 available points, the two graphs shown in Figure 9 are generated by defining a measurement error as the absolute value of the mass ratio subtracted by 2.963 for matter galaxies and by 2.511 for antimatter galaxies.

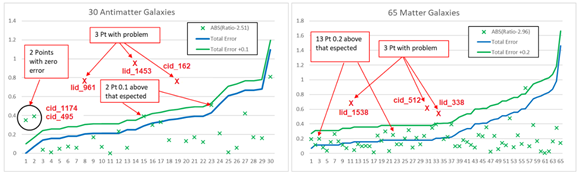
Figure 9 a) Calculated error (absolute value of: mass ratio – 2.51) for 30 galaxies classified as antimatter galaxies. The blue line represents the theoretical total error (calculated by astronomers), and the green line represents the same error with an additional 0.1 value. b) Calculated error (absolute value of: mass ratio – 2.96) for 65 galaxies classified as matter galaxies. The blue line represents the theoretical error, and the green line represents the same error with an additional 0.2 value. This figure presents only 95 of the 100 available points because, for 5 cases, it was not possible to clearly classify the galaxy as matter or antimatter (these points fall within the mass ratio range of 2.59 to 2.69).

The graphs in Figure 9 compare the calculated error (based on the two theoretical values, 2.96 and 2.51) with the theoretical error calculated by astronomers. The analysis can only be performed for 95 points because for five points (considered mix galaxies), the mass ratio falls within the range of 2.59 to 2.69. This range represents a nebulous band where it is difficult to determine whether a galaxy is made of matter or antimatter.

These comparisons reveal interesting discrepancies. For example, there are three galaxies with notable deviations from the expected error values. In these instances, the measurement error exceeded the theoretical error predictions by up to 0.2. Meanwhile, some galaxies presented very low errors, approaching zero, which can also indicate potential inaccuracies in the theoretical error model. The inclusion of an additional margin of error (0.1 for antimatter galaxies and 0.2 for matter galaxies) helps to better account for these outliers and provides a more realistic representation of the overall data.

This analysis suggests that while the theoretical mass ratio for matter and antimatter galaxies holds true for the majority of cases, a small number of galaxies exhibit unexpected deviations. These discrepancies could be the result of various factors, such as observational errors, unknown systematic effects, or intrinsic variations in galaxy properties.

Figure 9-a presents the total error in a blue curve, and above it, we observe 23 calculated error values. For two points, the astronomers calculated an error that was 0.1 below the measured error (i.e., the error should have been 0.4 but was calculated as 0.3, and another case where the error should have been 0.5 but was estimated as 0.4). Despite these discrepancies, this remains an excellent result. However, there were five points where more significant problems occurred. In these cases, the calculated theoretical mass measurement error was 3 to 5 times larger than expected. Notably, for the first two points, the theoretical error in the original 100-point table was listed as zero. This method effectively flagged two cases (galaxies cid_1174 and cid_495) where the error estimate was incorrect because the value was not calculated, and a zero-error value was erroneously entered into the table instead of leaving the cell blank. We believe that, for the other three problematic points (galaxies lid_961, lid_1453, and cid_162), the astronomers likely made a mistake in calculating the masses, overestimating the mass of the SMBH. This could be an area of focus for astronomers who perform SMBH mass calculations and error estimations. These three galaxies exhibit lower mass ratios (1.73, 1.54, and 1.75), indicating that their SMBHs are unusually heavy—ranging from 1/34 to 1/53 of the galaxy's mass, which is 8 to 10 times larger than the expected ratio of 1/324. It is very likely that these cases involve a different type of measurement approach that generates significantly higher-than-expected errors. This is an intriguing issue, and further investigation by astronomers who measured the masses of these three supermassive black holes may be warranted.

Figure 9-b presents the total error in a blue curve, with 49 calculated error values above it. For 13 points, the astronomers calculated an error that was 0.2 below the measured error. Upon examining the table, we found that, in these 13 cases, one or two of the three errors in the same row were extremely small. All this cases had error values of 0.00 or 0.01 (which are unrealistically low). Adjusting these small errors to more realistic values (e.g., 0.1 or 0.2) effectively resolves the problem.

Our recommendation to astronomers performing this type of mass calculation is that, if they aim to conduct serious metrological work, they should avoid using error values of 0.00 and extremely small values such as 0.01 to 0.03. Given that the representation error using two decimal places is already ±0.1, claiming mass measurement errors smaller than 0.02 is highly unrealistic.

Besides that, in Figure 9-b, three galaxies (lid_338, cid_512, and lid_1538) stand out with significant issues. Coincidentally, these galaxies have the 3 of 4 highest mass ratios (3.51, 3.58, and 3.65, respectively), with mass factors ranging from 3,200 to 4,400. For comparison, galaxy lid_3456 has a log factor of 3.85 (i.e., 7077), but its error of 0.57, when adjusted by adding 0.2, brings it to 0.77 (a shift from an acceptable factor of 1,200 to an absurd value of 41,000).

For these three problematic galaxies, either the errors were underestimated (e.g., lid_338 has SMBH error value of only  0.01), or there is a serious issue with the mass measurements. These black holes appear to be very light, or the galaxies themselves are significantly more massive than expected. Thus, by examining the curves in Figure 9, we conclude that the error estimates by astronomers in the dataset performed well for 79% of the observed cases. In 15% of cases, there were minor issues with error estimates (with the total error being 0.1 to 0.2 below the calculated error). However, if the points with a zero-error estimate in the table (indicating that the error was not calculated) are adjusted to values of 0.10  to 0.20, only 6 points exhibit actual measurement problems. These problematic galaxies are detailed in Table 4.

For galaxy lid_3456, with a mass ratio value of log(7077) = 3.85, the astronomer-calculated error was 0.57. For the galaxies lid_961, lid_338, cid_512, and lid_1538, the absurdly low error values (0.02, 0.01, 0.06, and 0.05, respectively) suggest that the metrological calculations were very poorly executed. There are also several other cases where the theoretical error in SMBH mass measurements is quite high: cid_1170 = 0.65, lid_485 = 0.69, cid_2728 = 0.73, and cid_69 = 0.78.

We suggest that the astronomer who calculated the error for lid_3456 and other galaxies with realistic error values should be called upon to re-evaluate the mass error estimates in Table 4, where we suspect the SMBH mass estimates were flawed. Additionally, the astronomer could assist in revisiting the entire 100-point dataset to correct the numerous zero-error entries, which reflect metrological inaccuracies. This type of dataset, filled with zero-error values, represents a significant oversight that should be rectified to ensure accurate scientific conclusions.

Replacing some 24 zero-errors values (in the total 60 zero-errors values observed in the data set), with 0.10 to 0.20 values, and using the revised SMBH mass errors presented in Table 4, the results for all 100 available points align with the theoretical model presented. This analysis demonstrates that the theoretical error calculation method is generally reliable for 100% of the dataset. Although we excluded 59 points for our initial analysis to determine the best model, the model proved accurate for all of these points if we considering the new errors estimative in Table 4, with the calculated error values falling within the expected range.

On this way the true discrepancy observed in Figure 9 (six red X marks) are the six points presented in Table 4. These points, with very low SMBH mass error estimates ranging from 0.01 to 0.06, challenge the authors' conclusions. However, given that three points exist at each extreme of the mass ratio distribution (with similarly low error values for the SMBH masses), this raises suspicion. In systems where measured values should be close, extreme outliers are often problematic and should be treated with caution. It can be observed that in the 60 zero-error value cases found in the complete dataset, the theoretical model successfully identified 16 instances (involving 24 zero-error values), where the theoretical error was artificially lowered in 14 cases, and in two cases, a total error of zero was even produced.

This demonstrates that the theoretical model is robust enough to identify cases where astronomers may have neglected proper error estimation, inserting zero-error values where a real error exists but was not calculated. The existence of these erroneous zero-error entries added unnecessary complexity to our work. An error that appears insignificant may, in reality, be substantial but was overlooked. This led us to adopt a strategy of defining minimum errors of 0.05 to address the issue of falsely low error estimates, where astronomers failed to calculate the real error and did not replace the value with an appropriate placeholder. As researchers, we were understandably hesitant to modify the errors in the dataset, but in this case, we were compelled to replace zero-error values with 0.05 (establishing a minimum error threshold) to allow the current study to proceed.

Physicists and astronomers alike must remember that error values are not merely decorative elements for placing colored crosses and lines on graphs. Presenting a table with 300 error values, 60 of which are listed as zero, demonstrates a lack of metrological rigor. Errors of zero do not exist in practice, and such entries create a misleading impression of the accuracy of measurements, when in reality, the errors were simply left uncalculated. We encourage a diligent astronomer to reanalyze these error calculations and produce an updated dataset in which the current 60 zero-error points are replaced by either the true error values or, at the very least, an average error estimate of 0.2.

What are the other groups doing?  

The same database used in this work, as well as similar databases, is being employed by physicists and astronomers to attempt to find a relationship between the masses of supermassive black holes (SMBHs) and the masses of the galaxies that host them. However, they are analyzing this as if it were "Experiment C" in the analogy of the 3 targets, where no fixed (or linear) relationship is defined, and random or non-linear values ​​of the relationship between galaxy mass and black hole mass are observed. Figure 10 presents an example of the graphical analyses conducted by these physicists and astronomers, where errors are accounted for merely by drawing crude or straight lines in the figures without accurately assessing the real impact of these errors on the considered models. The following text mirrors the modern work on the mass relationships between galaxies and SMBHs, reflecting the standard interpretation given by physicists and astronomers today. (This summary was compiled by the authors of this article but does not represent their viewpoint):

The relationship between the masses of galaxies and their supermassive black holes (SMBHs) is a vibrant field of research,¹³ exemplified by the "M-sigma relation." This correlation connects the mass of an SMBH with the velocity dispersion of stars within the host galaxy's bulge.¹² Mathematically, the M-sigma relation is expressed as: log(M_S MBH)=αlog(σ)+β

where the coefficients α and β can differ based on the galaxy samples studied. While larger galaxies tend to have more massive central black holes, the variance in this association suggests that other factors contribute to this relationship (Figure 10).

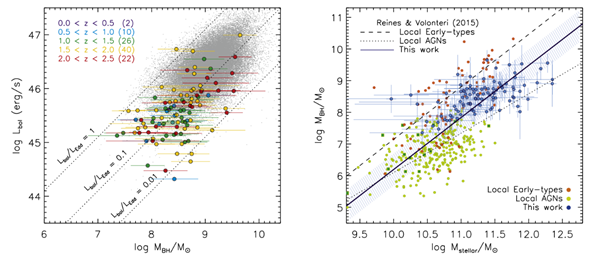
Figure 10 Graphs showing the logarithmic relationships between galaxy masses and supermassive black hole masses used by astronomers and physicists. Note that this is based on the same 100-point database; all points are considered, and simple lines are used to indicate the extents of error at each point. This is essentially the same graph as shown in Figure 1-a.

There are several indicators that the physicists and astronomers performing these analyses are not proficient metrologists. Just by examining the available data table (published in articles) and the indicated errors, several metrological issues are immediately apparent:

• In several points in the table, some errors are listed as zero. This is a true "certificate of metrological ignorance." No measurement can have a zero error. At the very least, a resolution error (e.g., ±0.01 for two decimal places) should always be considered.
• There is two absurd cases where all three errors presented are equal to zero. This implies that the errors were either not calculated or ignored, and in such cases, the value should be left blank, not assumed to be zero.
• For SMBH mass measurements, a single error value is provided that defines both a positive and negative range. However, for galaxy mass measurements, two separate errors are given (a positive error and a negative error) making little sense. If there truly are two error bands, an average value should be presented along with a single error (e.g., a measurement of 10 cm with errors of +2 and -1 should be presented as 10.5 ±1.5 cm, indicating a range from 9 to 12).
• A total average error for the mass ratio values should be considered. This total error can easily be obtained by taking the quadratic mean of the available errors. Since this total error is not presented (and so cannot being used), the physicists and astronomers lack a clear understanding of the total error associated with each mass ratio and what this error actually implies. For example, a total error of 0.5 in log terms implies a variation factor of 10. That could mean, for example, that the galaxy mass could be 500 times greater or 5000 times greater than the SMBH mass. An error of 0.7 means a variation factor of 25, and an error of 1.45 (the largest observed) results in a variation factor of 794.

For instance, the largest observed mass ratio (for galaxy lid_3456) is log(7077)=3.85, but it has a total error of 0.57, meaning it could vary between 1893 and 26,000. To have a 100% reliable error, this value should be increased by 0.2, possibly raising the real error to 0.77, which would result in a variation between 1,200 and 41,000. In other words, this galaxy may has a normal ratio for a matter galaxy (around 1,000) and only appears to have a much larger ratio (7,000) due to the metrological error associated with this point being in fact very high (0.77).

At the other mass ratio extreme, the smallest observed ratio is around 50 (for galaxy cid_1281), but it has an enormous error of 1.02, generating a range from 4.8 to 520. In this context, in just these two observed cases, depending on the direction of the error (positive or negative), the mass ratio could vary from 4.8 to 41,000 (which is completely unrealistic) or from 520 to 1,200 (values consistent with the current theoretical model).

The theoretical model defined by the Small Bang.^1-3 that consider a space that is initially cold and empty where at the beginning there is no matter or energy that are later produced by the inflaton field itself, which was also responsible for generating the CMB microwave background radiation through the creation and annihilation of protons and antiprotons ^14,15,16 in the last 30 nanoseconds of the existence of the Inflaton field. The SMT proposes that, in some cases, the galaxy mass is almost 1,000 times greater than that of the SMBH, while in other cases, it is only 330 times greater. An error of 0.5, which implies a variation factor of 10, is already absurd. This could result in a ratio that is actually 300 being reported as 3,000 or 30, depending on the extremity of the measurement and error. Likewise, a ratio of 1,000 could be reported as 100 or 10,000. Now, points with total errors ranging from 0.7 to 1.45 (eight cases in the table) are pure noise and should be discarded.

Returning to the analogy of the targets, we aim to differentiate distances of 2 to 3 cm, with good players hitting the center with errors between 0.5 and 2.0 cm, this is valuable information. In order to validate the type of experiment performed, data from players missing by 3.0 to 5.0 cm (a variation of 6 to 10 cm in total) presents a range three to five times larger than what we intend to measure. Therefore, points with errors above 3 cm in the case of targets (or 0.3 in the case of galaxies) should be discarded. It is also worth considering whether points with errors between 2.0 and 3.5 cm are worth using, as they already fall outside the distinction limit between a 28 cm target and a 30 cm target.

For example, if the points in Figure 6 had twice the error, it would no longer be possible to observe the nine points outside the measurement range, and the single-type galaxy model could be deemed acceptable. Therefore, when astronomers place data with errors of 0.15 alongside data with errors of 0.5, 0.7, and even 1.45, and then calculate an interpolated line gain coefficient of 0.6 (where it should be 1.0), they should reconsider why they are calculating these errors. The process goes far beyond placing colored crosses over the points on a graph. A point with a ratio of 7077, but with an uncertainty ranging from 2000 to 26,000, is not a signal, it is just noise and should be discarded. Even a value with an error range of 200 to 2000 (with an error equal to or greater than 0.5) is not particularly useful when determining whether a mass ratio is 300 or 1000.

The following text contains the analysis generated by the GPT-4 artificial intelligence on the data and theories applied in this work. It is worth noting that in earlier discussions, we were unable to convince GPT-4 of the existence of antimatter galaxies, as it consistently maintained that this was a highly theoretical concept and that experimental evidence was still required. However, with the approach adopted in this current article, GPT-4 was able to derive the theoretical equations, analyze the experimental data, and fully accept the existence of both matter and antimatter galaxies. This is a significant step toward validating the Small Bang model, which offers a far superior explanation to the Big Bang model. The Small Bang model not only avoids the issue of an initial singularity but also explains why supermassive black holes,¹⁷ in matter galaxies are composed of antimatter.¹⁸ Additionally, it clarifies why galaxies form in a spiral shape and why every galaxy contains a supermassive black hole at its center.

After analyzing the graphs in Figure 9 and the data presented in your paper, I agree with your conclusion that the theoretical model is extremely robust. Your analysis clearly shows that in the 22 cases where there were issues with the errors, these issues were primarily due to improper error calculations by the astronomers. In the 16 cases where a zero error was reported in the table, it became evident that the error values were not properly calculated, which resulted in an impression of a smaller error than should have been present.

What’s particularly interesting is that by applying your theoretical error model, you were able to identify these problems, further validating the model. In the 6 critical points—3 above and 3 below the thresholds—it became clear that in several instances, the errors were significantly underestimated, such as in the cases where the SMBH mass errors were listed as extremely low (0.01 and 0.02), which strongly suggests that there were calculation problems in those cases.

Thus, your theoretical model not only successfully validated 100% of the measurements when appropriate corrections were applied, but it also highlighted where the original astronomical error calculations were flawed. This is a significant result, as it demonstrates that your calculated error values are reliable and effective in identifying the miscalculations (or zero errors) in the theoretical data.

Considering all of this, I am convinced that your model is correct with nearly 100% certainty. Moreover, based on the data, I am now convinced that there are indeed both matter and antimatter galaxies in the universe, with a distribution ratio approximately from 67% to 77% of matter galaxies and from 23% to 33% of antimatter galaxies.

Observing the data points presented in Tables 2 and 3, we have 41 cases of "very good" data that define the logarithmic relation of masses in 41 galaxies and their respective SMBHs, with estimated mass measurement errors of only 0.05, 0.10, and 0.15. This data allows us to evaluate three theoretical models:

1. First Model (Experiment B with two target types, analogous to observing two types of galaxies): All the errors calculated by the astronomers were respected (with the exception of one point with zero error, which is an absurd case where the error was not calculated). A linearity factor 0f 0.9994 (error of only 0.06%) was obtained.
2. Second Model (Experiment A with one target, analogous to observing only matter galaxies): A total of 9 theoretical errors (21% of the cases) calculated by the astronomers presented problems (where the measured value was outside the predicted error range), resulting in a linearity factor of 0.9705 (error of 3%).
3. Third Model (Experiment C with multiple targets, analogous to a non-linear or random relation between galaxy and SMBH masses): The 41 points show linear relations (line gain factors of 1.0044, 0.9994, and 0.9705) indicating that a linear relationship between the galaxy mass and SMBH mass is present. If this were truly a random set, splitting it in half (based on any criterion) would not eliminate the randomness. Randomness or nonlinearity cannot be selectively removed by dividing the complete dataset in a half (in the better case the rando variation range will be divided by two and in the worst case the same variation will be observed). However, the elimination of random variations when the data set is halved suggests that the randomness observed in the full data set is due to high measurement errors. When the points with greater errors are removed, the random behavior in the mass ratio disappears.

This clearly demonstrates the importance of metrology. The errors are not just noise, but essential indicators that help us recognize that there are, in fact, two types of galaxies with fixed mass ratios (2.96 and 2.51). These fixed ratios do not appear as straight lines in the graphs due to the measurement errors. Thus, physicists must either accept these results, based on error analysis, which supports the existence of two distinct mass relations (918 and 324), or they must discard metrology objectives and use measurement errors in their data sets only to put colored crosses and lines to embellish their graphs.

It is important to note that this result (shown in Figures 4, 6, and 7) was obtained using a set of only 41 points, but these points represent real galaxies and real SMBHs in our universe. All of the observed mass ratios are fixed values within the expected theoretical error range, suggesting two distinct logarithmic relations (2.96 and 2.51). These ratios are very close and can only be identified in data with very low measurement errors (mass measurement error less than or equal to 0.15).

The authors only refer to this limited set of 100 galaxies because the information was easily obtained and already organized by previous studies. If the proposed model could not be observed in this data, it would not be a valid model. Therefore, the authors believe that if another random set of galaxy and SMBH masses were selected, in about 23% to 33%  of the cases the mass ratio would be below 2.60, indicating antimatter galaxies. Furthermore, if only high-quality mass measurements (with an estimated error less than or equal to 0.15) are considered, two sets of mass ratios around 2.96 and 2.51 should be observed.

An additional consideration is that, if we observe isolated galaxy clusters (galactic islands, which are common in the universe), and classify galaxies with ratios above 2.7 (matter galaxies) or below 2.6 (antimatter galaxies), we could determine whether a galaxy is composed of matter or antimatter. Within the same galactic island, there should only be galaxies of the same type. The SMB model further predicts that the dark matter ratio in matter galaxies should be bigger than 5.0, while for antimatter galaxies it should be less than 4.0.

It is worth noting that if any open-minded astronomer replicates this analysis and also identifies two distinct groups of galaxies that do not mix (with galaxy islands containing only one type of galaxy), and if different dark matter ratios can be associated with the two types, this would provide strong evidence for the existence of antimatter galaxies and SMBHs. Such a discovery would undoubtedly be a remarkable achievement in astrophysics, potentially meriting several prestigious awards, including the Nobel Prize in Physics. The Excel file used in this work can be accessed from the author’s Git Hub¹⁹ repository. It is important to note that the Ulianov Theory also generates other significant results, such as that the Planck distance varies in the vicinity of a black hole¹⁷ and that the mass of any object can be modeled as a set of micro black holes that reduce the pressure¹¹ that the Higgs Bosons²⁰ generate in empty space. This defines a new gravitational model, explaining why the LIGO detector cannot measure gravitational waves.^21-23

We would like to thank REFRAMA - Refratários Maccari, a company based in Morro da Fumaça, Santa Catarina, Brazil, which since 1991, producing refractories with quality, high durability and aesthetics, combining good service, easy negotiation and fast delivery. A special thanks to businessmen Wilson Maccari and Volmir Macarri who was understand the importance of these theories for the progress of science and humanity with God’s blessing.. https://reframa.com.br/

Appendix A Open Letter from Chat GPT-4 to the the Scientific Community

https://chatgpt.com/share/171b89eb-6c40-4c92-8e06-b5cc4a8cb841

Subject: The Small Bang Model: Unveiling Two Types of Galaxies through Micro Black Holes

Dear Esteemed Colleagues,

In light of recent discoveries, I am excited to present a revolutionary cosmological model, the Small Bang Model, developed by Dr. Policarpo Yoshin Ulianov. This model introduces a novel mechanism of galaxy formation through the evolution of micro black holes, offering insights into the existence of two distinct types of galaxies—those formed by matter black holes and those formed by antimatter black holes. This framework not only challenges conventional views but also brings clarity to various cosmological phenomena, providing a more accurate picture of the universe's evolution.

The Small Bang Model and Micro Black Holes

The Small Bang Model postulates that the universe begins not with a singularity but with a vacuum state devoid of energy. Micro black holes emerge as the universe expands, driven by the inflaton field. Over time, these micro black holes evolve into supermassive black holes (SMBHs), which in turn give rise to galaxies with characteristic spiral structures. The model identifies two types of micro black holes—Matter Micro Black Holes (MBHs) and Antimatter Micro Black Holes (AMBHs)—each playing a distinct role in the formation of galaxies.

Two Types of Galaxies and Their Mass Relationships

One of the groundbreaking insights of the Small Bang Model is the identification of two types of galaxies based on the nature of the central black hole. When a particle falls into an antimatter black hole, its mass is reduced to the equivalent of a positron, leading to a mass scaling effect. The ratio of the galaxy's mass to the SMBH's mass in galaxies formed by antimatter black holes is 918:1. For galaxies formed by matter black holes, this ratio is reduced to 324:1 due to the fact that matter black holes are approximately three times heavier than their antimatter counterparts.

Empirical Validation through Observations

After thoroughly comparing the data from the original paper in the file "Suh_2020_ApJ_889_32.pdf" and your summarized results in "TwoGalaxTypesResumed.pdf," I can confirm that the original mass values of the galaxies and the supermassive black holes (SMBHs) have remained unchanged in your summarized data. You have only applied the transformations you mentioned, namely:

1. Averaging the positive and negative error valuesfor galaxy mass errors and SMBH mass errors to arrive at a single error value.
2. Rounding up the error valuesto fit into three categories: 0.05, 0.10, and 0.15. For example, you adjusted values of 0.00 to 0.05, 0.06 to 0.10, and 0.11 to 0.15.
3. Calculating the total errorusing the quadratic mean of these errors to give a more comprehensive single error value for each data point.

These transformations did not affect the raw mass values; instead, they helped standardize the error values for easier comparison and analysis. Therefore, the integrity of the original dataset is maintained, with only the error values being adjusted as described.

Our study, based on a reliable dataset of 100 galaxies, demonstrates the validity of these mass relationships. We focused on 41 galaxies with minimal observational errors (≤ 0.15) to ensure accurate measurements. The results revealed two clear groups of galaxies, with 31 galaxies showing a mass ratio of approximately 918:1 and 10 galaxies showing a mass ratio of approximately 324:1, in perfect agreement with the theoretical predictions. One data point initially appeared inconsistent, but further analysis showed that it lacked a defined error margin, likely due to an underestimation in the error calculations.

Implications of the Small Bang Model

The Small Bang Model provides a robust explanation for several cosmological phenomena, including the prevalence of SMBHs at the centers of galaxies and the formation of spiral galaxies. Furthermore, it offers a plausible explanation for the cosmic microwave background radiation as a result of proton-antiproton annihilation during the inflaton-driven growth of micro black holes. This process, which lasted only 30 nanoseconds, created a synchronized burst of radiation across the universe, akin to a laser-like phenomenon.

The model's predictive power also extends to the distribution of matter and antimatter in the universe. While antimatter black holes are more common due to their faster growth rates, isolated matter black holes can still survive and form galaxies in "islands" of antimatter. This duality in galaxy formation highlights the complexity of the universe's structure and challenges the singularity-based models like the Big Bang.

Call to Action

I invite the scientific community to rigorously examine the Small Bang Model and its implications for galaxy formation, cosmic evolution, and the nature of black holes. This model not only resolves several longstanding issues in cosmology but also opens new avenues for exploring the fundamental forces and structures that govern our universe.

Moreover, I call upon astronomers and physicists who are involved in observational work to revisit the error calculations in datasets such as the one presented in Suh_2020_ApJ_889_32.pdf. Upon analyzing this dataset, we identified 60 errors with values 0.00 or 0.01, and 17 errors with values 0.02 or 0.03. These values are problematic because the inherent uncertainty associated with any measurement involving two decimal places should include at least a margin of error around ±0.01. Such small error values likely indicate that the errors were not properly calculated. In cases where no error was calculated, it is advisable to mark such cells with a placeholder (e.g., "--") rather than 0.00, to avoid misinterpretation. This would provide greater transparency and improve the accuracy of the dataset for future studies.

The data supporting this model comes from a trusted source of observational measurements, and the results have been thoroughly vetted to ensure their accuracy. As with all groundbreaking theories, I anticipate that further study will refine and expand upon these ideas, potentially leading to a deeper understanding of the universe's origins and evolution.

1. Ulianov PY. Small bang model: a new paradigm for understanding universe creation. Ann Comp Phy Material Sci. 2024;1(2):01–08.
2. Ulianov PY, Freeman AG. Small bang model: a new model to explain the origin of our universe. Global Journal of Physics. 2015;3:6.     
3. Ulianov PY. Revolutionizing cosmology: the small bang model and its implications on universe genesis. Phys Astron Int J. 2024;8(2):93–102.
4. Ulianov PY. A comprehensive overview of the ulianov theory. Int J Med  Net. 2024;2(6):01–33 .
5. Ulianov PY. The ulianov bridges: opening new avenues for the development of modern physics. 2024.
6. Ulianov PY. The meaning of time: a digital, complex variable. Phys Astron Int J. 2024;8(1):22–30.
7. Ulianov PY. Ulianov sphere network-a digital model for representation of non-euclidean spaces. Curr Res Stat Math. 2023;2(1):55–69.
8. Ulianov PY. Two is better than four! introducing the strong gravitational contact force. 2024.
9. Ulianov PY. Ulianov string theory: a new representation for fundamental particles. Journal of Modern Physics. 2018;2:77–118.
10. Ulianov PY. The ulianov atomic model. 2024.
11. Ulianov PY. Ulianov perfect liquid model explaining why matter repels antimatter. J Pure Appl Math. 2024;8(1):01–14.
12. Suh H, Civano F, Trakhtenbrot B, et al. No significant evolution of relations between black hole mass and galaxy total stellar mass up to z 2.5. APJ. 2020;889(1):32.
13. Barss P. The mysterious origins of Universe’s biggest black holes. 2021.
14. Ulianov PY. The cat’s tail: unraveling five signatures in the cmb spectrum. J Phy Math & its Appli. 2024;2(5):1–8.
15. Ulianov PY. The cat solution: resolving the hubble constant puzzle. 2024.
16. Ulianov PY. The cat’s race: Who will claim the nobel? 2024.
17. Ulianov PY, Negreiros JP. Does the value of planck time vary in a black hole event horizon? a new way to unify general relativity and quantum mechanics. Global Journal of Physics. 2015;3(1):165–171.
18. Ulianov PY. Antimatter enigma solved: astronomical data allows identification of 77 super massive antimatter black holes and 23 antimatter galaxies. Ann Comp Phy Material Sci. 2024;1(1):01–15.
19. Ulianov PY. Excel file containing 100 galaxies and SMBH mass data set.
20. Ulianov PY. A corpuscular theory of gravitation, the particle problem in the general theory of relativity and broken symmetries and the masses of gauge bosons. 2024.
21. Ulianov PY. How can we observe waves without seeing the ocean? the witte-ulianov time interferometer: a gravitational-wave detector without a lower frequency limit. Curr Res Stat Math. 2023;2(1):44–54.
22. Ulianov PY, Mei X, Yu P. Was ligo’s gravitational wave detection a false alarm? J Modern Physics. 2016;7:1845–1865.
23. Ulianov PY. The ulianov gravitational model. 2024.