In this paper, we propose a novel method to treat the electroweak symmetry braking. In this method, a conformal metric is employed and the Higgs field is scaled owing to the conformal function and the mass parameters of the quadratic term of the Higgs potential has a time dependence through the conformal function, and it induces the phase transition. Quantization of the Higgs field is induced associated with the canonical quantization of general relativity. The cosmic inflation and the electroweak phase–transition are discussed in a framework of the scaled field. The Friedmann equations are numerically solved and an example of a possible solution to match with the cosmic inflation scenario is given in this research.

Keywords: electroweak symmetry, conformal metric, higgs potential, cosmic inflation, phase transition, friedmann equations

After the discovery of the Higgs boson^1,2 in 2012, the standard theory of particle physics (SM) is established as the canon of a fundamental physics. According to the SM, the electroweak symmetry is spontaneously broken owing to the Higgs mechanism,^3–5 and the current universe is considered to be filled with the Higgs filed which has a finite vacuum expectation–value. On the other hand, the electroweak symmetry is expected to be in the unbroken phase in the early universe before the cosmic inflation. A standard scenario of the big–bang cosmology is that the electroweak phase–transition from the unbroken to the broken phases might occur during (or at the beginning of) the cosmic inflation, and the universe was re–heated after the cosmic inflation, and then the big–bang started.

The cosmic inflation was proposed to solve the flatness and horizon problems by several authors independently^6–9 in 1980. In these “old” models, the cosmic inflation is induced by the Higgs filed (or some scalar filed which is referred to as the inflaton field), and it is terminated when the electroweak phase–transition of the first–kind occurred. These models are suffered by the vacuum–bubble problem which destroyed isotropy of the universe. In 1982, the “new” inflation models^10–12 are proposed which utilize the phase–transition of second–kind to avoid the vacuum–bubble problem. The inflation terminated moderately in the “new” models. Although these “new’ models can solve the vacuum–bubble problem, they require a fine tunning of initial parameters to realize the cosmic inflation for a enough time duration. Yet other models of the cosmic inflation was proposed such as the chaotic inflation,¹³ the Higgs inflation with non–minimal coupling to gravity¹⁴ and so on.

In any inflation scenario, the electroweak phase–transition is critical to induce and terminate the cosmic inflation. However, a widely accepted mechanism to induce the symmetry braking is not established yet. The early scenario¹⁵ of the symmetry braking using higher–order radiative corrections is now excluded in precise measurements of the SM parameters. The radiative braking scenario is re–examined and concluded that it is still viable if an additional scalar field is introduced.¹⁶ This scenario is intensively investigated in literatures.^17,18 Recently, this scenario is extended¹⁹ using the classically conformal $ℬ-ℒ$ extension of the SM.²⁰

We propose a new and novel mechanism of the electroweak symmetry braking in this study. In the proposed method, which is referred to as the “scaled scalar–field method”, a conformal metric is employed, and the Higgs field is scaled owing to the conformal function. Quantization of the Higgs field is induced due to the canonical quantization of general relativity. In consequence, a mass parameter of the Higgs field (a quadratic term of the Higgs potential) has the time dependence through the conformal function, and it causes the phase transition. The scaled scalar–field method is introduced in section 2 after a brief explanation of our geometrical setups. The Friedmann equation which governs the cosmic inflation is formulated using the scaled scalar–field method in section 3.1. After some appropriate approximation, the Friedmann equations are numerically solved and an existence of a possible solution to match with the cosmic inflation scenario is shown in section 3.2. A summary of the method and consequences on the inflation scenario is provided in section 4.

Geometrical setups

A scalar field defined on a four dimensional space time manifold $ℳ$ with a $GL\mathrm{<mo\; stretchy="false">(</mo>1,3<mo\; stretchy="false">)</mo>}$ symmetry is considered in this study. First, classical general relativity and the scalar field defined on $ℳ$ are summarized using a vierbein formalism. The formalism and terminology in this study follow our previous works.21–23 At each point on $ℳ$ , a local Lorentz manifold $M$ with a Poincaé symmetry $ISO\mathrm{<mo\; stretchy="false">(</mo>1,3<mo\; stretchy="false">)</mo><mo>=</mo>}SO\mathrm{<mo\; stretchy="false">(</mo>1,3<mo\; stretchy="false">)</mo>}⋉T^4$ is associated, where $T^4$ is a four–dimensional translation group. On a open neighborhood around any point $x\in U\subset ℳ$ , a trivial frame vector is expressed as $x^{\mu }$ , and a trivial vector bundle (frame bundle) can be introduced. An orthonormal basis of ${\partial }_{\mu }$ in $Tℳ$ and $d{x}^{\mu }$ in $T^{\mathrm{<mo>*</mo>}}ℳ$ are also introduced. A short–hand notations of ${\partial }_{\mu }\mathrm{<mo>=</mo>}\partial \mathrm{<mo>/</mo>}\partial x^{\mu }$ are used through out this study. The Einstein’s equivalent theorem insists an existence of an isomorphism $ℳ\to M$ at any point in $ℳ$ . A metric tensor $g_{••}$ in $ℳ$ is mapped to ${\eta }_{••}$ in $M$ using a vierbein ${ℰ}_{\mu }^a$ as $g_{\mu \nu }\mathrm{<mo>=</mo>}{\eta }_{ab}{ℰ}_{\mu }^a{ℰ}_{\nu }^b$ . An orthogonal basis in $T^{\mathrm{<mo>*</mo>}}M$ and $TM$ are respectively expressed as $d{x}^a\mathrm{<mo>=</mo>}{ℰ}_{\mu }^{a}d{x}^{\mu }$ and ${\partial }_a\mathrm{<mo>=</mo>}{ℰ}_a^{\mu }{\partial }_{\mu }$ using a vierbein and its inverse. The Einstein convention for repeated indices is used though out this study. In addition, Greek and Roman indices are used for a coordinate on $ℳ$ and $M$ , respectively. A local Lorentz metric and the Levi Civita tensor are respectively defined as ${\eta }_{••}\mathrm{<mo>=</mo>}diag\mathrm{<mo\; stretchy="false">(</mo>1,}-\mathrm{1,}-\mathrm{1,}-\mathrm{1<mo\; stretchy="false">)</mo>}$ and ${\epsilon }_{••••}$ with ${\epsilon }_{0123}\mathrm{<mo>=</mo>1}$ . Dummy Roman–indices are often abbreviate to dots (or asterisks), when the index pairing of the Einstein convention is obvious, such as ${\eta }_{ab}{ℰ}_{\mu }^a{ℰ}_{\nu }^b\mathrm{<mo>=</mo>}{\eta }_{\cdot \cdot }{ℰ}_{\mu }^{\cdot }{ℰ}_{\nu }^{\cdot }$ . When multiple dots appear in an expression, pairing must be a left–to–right order at both upper and lower indices, e.g. ${\mathfrak{a}}_{\cdot \cdot }\wedge {\mathfrak{b}}^{\cdot \cdot }\mathrm{<mo>=</mo>}{\mathfrak{a}}_{ab}\wedge {\mathfrak{b}}^{ab}$ . A principal connection of the fiber bundle $\mathfrak{s}\mathfrak{o}\mathrm{<mo\; stretchy="false">(</mo>1,3<mo\; stretchy="false">)</mo>}\to M$ is represented as ${\omega }_{\mu \mathrm{<mi>\; </mi>}b}^{\mathrm{<mi>\; </mi>}a}$ , which is referred to as the spin connection. The spin connection satisfies a metric compatibility condition as ${\omega }_{\mu \mathrm{<mi>\; </mi>}\cdot }^{\mathrm{<mi>\; </mi>}a}{\eta }^{\cdot b}\mathrm{<mo>=</mo>}{\omega }_{\mu }^{\mathrm{<mi>\; </mi>}ab}\mathrm{<mo>=</mo>}-{\omega }_{\mu }^{\mathrm{<mi>\; </mi>}ba}$ . A vierbein for ${\mathfrak{e}}^a\mathrm{<mo>=</mo>}{ℰ}_{\mu }^{a}d{x}^{\mu }$ and a $GL\mathrm{<mo\; stretchy="false">(</mo>1,3<mo\; stretchy="false">)</mo>}$ invariant volume form $\mathfrak{v}\mathrm{<mo>=</mo>}{\epsilon }_{\cdot \cdot \cdot \cdot }{\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\mathrm{<mo>/</mo>4<mo>!</mo>}$ are introduced. Similarly, the three–dimensional volume form and two–dimensional surface form are also introduced as ${\mathfrak{V}}_a\mathrm{<mo>=</mo>}{\epsilon }_{a\cdots }{\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\mathrm{<mo>/</mo>3<mo>!</mo>}$ and ${\mathfrak{S}}_{ab}\mathrm{<mo>=</mo>}{\epsilon }_{ab\cdot \cdot }{\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\mathrm{<mo>/</mo>2}$ , respectively. The volume form ${\mathfrak{V}}_a$ is a three–dimensional volume perpendicular to ${\mathfrak{e}}^a$ , and the surface form ${\mathfrak{S}}_{ab}$ is a two–dimensional plane perpendicular to both ${\mathfrak{e}}^a$ and ${\mathfrak{e}}^b$ . Fraktur letters are used for differential forms. A unit of $c\mathrm{<mo>=</mo>1}$ is used while the reduced Planck constant $\hslash$ and Newtonian gravitational constant $G$ (or the Einstein constant $\kappa \mathrm{<mo>=</mo>4}\pi G$ in our convention) written explicitly. In this units, there are two physical dimensions, the length and mass dimensions, which are denoted as $L$ and $M$ , respectively.

The Lagrangian for pure gravity without the cosmological term and matter fields is expressed as

${\mathfrak{L}}_G\mathrm{<mo>=</mo>}\frac{1}{2}{\mathfrak{S}}_{\cdot \cdot }\wedge {\Re }^{\cdot \cdot }\mathrm{,}$ (1)

${\Re }^{ab}\mathrm{<mo>=</mo>}d{\mathfrak{w}}^{ab}+{\mathfrak{w}}_{\mathrm{<mi>\; </mi>}\cdot }^a\wedge {\mathfrak{w}}^{\cdot b}\mathrm{,}$ (2)

where ${\mathfrak{w}}^{••}$ is the spin one–form, which is defined as ${\mathfrak{w}}^{ab}\mathrm{<mo>=</mo>}{\omega }_{\mu \mathrm{<mi>\; </mi>}\cdot }^{\mathrm{<mi>\; </mi>}a}{\eta }^{\cdot b}d{x}^{\mu }$ . A two form ${\Re }^{••}$ is referred to as the curvature form, that is a rank– $2$ Lorentz tensor on $M$ .

A Lagrangian of a scalar field $\phi \mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}$ can be expressed in the vierbein formalism as

${\mathfrak{L}}_S\mathrm{<mo>=</mo>}\frac{1}{2}\frac{1}{\mathrm{3<mo>!</mo>}}{\mathfrak{S}}_{\cdot \cdot }\wedge \left({\eta }^{\ast \ast }{\iota }_{\ast }{\mathfrak{s}}^{\cdot }\wedge {\iota }_{\ast }{\mathfrak{s}}^{\cdot }-V\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}{\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^{\cdot }\right)\mathrm{,}$ (3)

where $V\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}$ is a potential energy. A scalar–field two–form ${\mathfrak{s}}^{•}$ is defined as

${\mathfrak{s}}^a\mathrm{<mo>=</mo>}d\phi \wedge {\mathfrak{e}}^a\mathrm{<mo>=</mo>}\left({\partial }_{\cdot }\phi \right){\mathfrak{e}}^{\cdot }\wedge {\mathfrak{e}}^a\mathrm{.}$ (4)

Here ${\iota }_a\mathrm{<mo>=</mo>}{\iota }_{{\xi }^a}$ is a contraction operator with respect to the trivial coordinate–vector field ${\xi }^a\mathrm{<mo>=</mo>}{\eta }^{a\cdot }{ℰ}_{\cdot }^{\mu }{\partial }_{\mu }$ . A physical dimension of the scalar field is set as $L^{-1}$ in this study. In consequence, a Lagrangian form has null physical dimension as

$\left[\phi \right]\mathrm{<mo>=</mo>}{L}^{-1}\to \{\begin{array}{l}\left[{\iota }_{•}{\mathfrak{s}}^{•}\right]\mathrm{<mo>=</mo>}{L}^{-1}\hfill \\ \left[V\right]\mathrm{<mo>=</mo>}{L}^{-4}\hfill \end{array}\to \left[{\mathfrak{L}}_S\right]\mathrm{<mo>=</mo>1,}$ (5)

where $\mathrm{<mo\; stretchy="false">[</mo>}•\mathrm{<mo\; stretchy="false">]</mo>}$ shows the physical dimension of a quantity $•$ . On the other hand, the gravitational Lagrangian has a length square dimension $\mathrm{<mo\; stretchy="false">[</mo>}{\mathfrak{L}}_G\mathrm{<mo\; stretchy="false">]</mo><mo>=</mo>}{L}^2$ . An action integral is defined as

$ℐ\mathrm{<mo>=</mo>}{\displaystyle \int }\mathrm{<mo\; stretchy="false">(</mo>}\frac{1}{\kappa \hslash }{\mathfrak{L}}_G+2{\mathfrak{L}}_S\mathrm{<mo\; stretchy="false">)</mo>.}$ (6)

Physical constants in front of the gravitational and scalar–field Lagrangian are chosen to adjust the physical dimension of the action integral to be null. Owing to require a stationary condition on a variation of the action integral with respect to the vierbein form ${\delta }_{\mathfrak{e}}ℐ\mathrm{<mo>=</mo>0}$ , one can obtain the Euler–Lagrange equation as

$\frac{1}{2}{\epsilon }_{a\cdot \cdot \cdot }{\Re }^{\cdot \cdot }\wedge {\mathfrak{e}}^{\cdot }\mathrm{<mo>=</mo>}-\kappa \hslash \mathrm{<mi>\; </mi>}{\mathfrak{t}}_a\mathrm{,}$ (7)

where ${\mathfrak{t}}_a$ is the energy–momentum three–form of the scalar field, which can be represented as

${\mathfrak{t}}_a\mathrm{<mo>=</mo>}-\frac{1}{\mathrm{3<mo>!</mo>}}{\epsilon }_{a\cdots }\mathrm{<mo\; stretchy="false">(</mo>}{\iota }_{\ast }{\mathfrak{s}}^{\cdot }\mathrm{<mo\; stretchy="false">)</mo>}\wedge \mathrm{<mo\; stretchy="false">(</mo>}{\iota }^{\ast }{\mathfrak{s}}^{\cdot }\mathrm{<mo\; stretchy="false">)</mo>}\wedge {\mathfrak{e}}^{\cdot }+V\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}{\mathfrak{V}}_a\mathrm{.}$ (8)

Here, rising and lowering Roman indices are performed using a Lorentz metric tensor, e.g. ${\iota }^a{\mathfrak{s}}^b\mathrm{<mo>=</mo>}{\eta }^{a\cdot }{\iota }_{\cdot }{\mathfrak{e}}^b$ . A torsionless condition and Klein–Gordon equation can be obtained from ${\delta }_{\mathrm{<mo\; stretchy="false">(</mo>}\mathfrak{w}\mathrm{,}d\mathfrak{w}\mathrm{<mo\; stretchy="false">)</mo>}}ℐ\mathrm{<mo>=</mo>0}$ and ${\delta }_{\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{,}d\phi \mathrm{<mo\; stretchy="false">)</mo>}}ℐ\mathrm{<mo>=</mo>0}$ , respectively.

The scalar–filed Lagrangian ${\mathfrak{L}}_S$ given in (3) can be expressed using a trivial frame vector in $M$ or $ℳ$ as

$\mathrm{<mo\; stretchy="false">(</mo>3<mo\; stretchy="false">)</mo><mo>=</mo>}\mathfrak{v}\left[\frac{1}{2}{\eta }^{\cdot \cdot }{\partial }_{\cdot }\phi \mathrm{<mi>\; </mi>}{\partial }_{\cdot }\phi -V\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}\right]\mathrm{,}$

$\mathrm{<mo>=</mo>}\sqrt{-g}d{x}^0\wedge d{x}^1\wedge d{x}^2\wedge d{x}^3\left[\frac{1}{2}{g}^{{\mu }_1{\mu }_2}{\partial }_{{\mu }_1}\phi \mathrm{<mi>\; </mi>}{\partial }_{{\mu }_2}\phi -V\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo>}\right]\mathrm{,}$ (9)

where $g$ is a determinant of a metric tensor $g^{••}$ . Here a relation ${\iota }_a{\mathfrak{e}}^b\mathrm{<mo>=</mo>}{\delta }_a^b$ is used. The Einstein equation (7) can be expressed using components of a trivial basis on $M$ as

$R_{ab}-\frac{1}{2}{\eta }_{ab}R\mathrm{<mo>=</mo>}-2\kappa \hslash \mathrm{<mi>\; </mi>}{T}_{ab}\mathrm{,}$ (10)

$T_{ab}\mathrm{<mo>=</mo>}{\partial }_a\phi \mathrm{<mi>\; </mi>}{\partial }_b\phi -\frac{1}{2}{\eta }_{ab}{\partial }_{\cdot }\phi \mathrm{<mi>\; </mi>}{\partial }^{\cdot }\phi +{\eta }_{ab}V\mathrm{,}$ (11)

where $R_{••}$ and $R$ are the Ricci and scalar curvature, respectively. An energy–momentum tensor $T_{••}$ is defined through the relation ${\mathfrak{t}}_a\mathrm{<mo>=</mo>}{\mathfrak{V}}_{\cdot }{T}_{\mathrm{<mi>\; </mi>}a}^{\cdot }$ .

Conformal metric and scaled field method

The Friedmann–Lemaître–Robertson–Walker (FLRW) metric^24–27 is considered in the homogeneous and isotropic universe using a coordinate $\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{,}r\mathrm{,}\theta \mathrm{,}\varphi \mathrm{<mo\; stretchy="false">)</mo>}$ on $ℳ$ such as;

$d{s}^2\mathrm{<mo>=</mo>}d{t}^2-{\Omega }^2\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\left(f^{-2}\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}d{r}^2+r^{2}d{\theta }^2+r^2{{\displaystyle \sin }}^2\theta d{\varphi }^2\right)\mathrm{,}$ (12)

where $f^2\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}-K{r}^2$ , and $K$ is a constant related the space–time curvature. This metric can be expressed using a conformal time $\tau \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\displaystyle \int }d\tilde{t}\mathrm{<mo>/</mo>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}\tilde{t}\mathrm{<mo\; stretchy="false">)</mo>}$ as

$\mathrm{<mo\; stretchy="false">(</mo>12<mo\; stretchy="false">)</mo><mo>=</mo>}{\Omega }^2\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}\left(d{\tau }^2-f^{-2}\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}d{r}^2-r^{2}d{\theta }^2-r^2{{\displaystyle \sin }}^2\theta d{\varphi }^2\right)\mathrm{.}$ (13)

From the metric (13) and the torsion–less condition, the spin form can be obtained as

${\mathfrak{w}}^{••}\mathrm{<mo>=</mo>}\left(\begin{array}{cccc}0& H{f}^{-1}\mathrm{<mi>\; </mi>}dr\mathrm{<mi>\; </mi>}& H\mathrm{<mi>\; </mi>}rd\theta & H\mathrm{<mi>\; </mi>}r\sin \theta d\varphi \\ \mathrm{<mi>\; </mi>}& 0& -f\mathrm{<mi>\; </mi>}d\theta & -f\mathrm{<mi>\; </mi>}\sin \theta d\varphi \\ \mathrm{<mi>\; </mi>}& \mathrm{<mi>\; </mi>}& 0& \mathrm{<mi>\; </mi><mi>\; </mi>}-\cos \theta d\varphi \\ \mathrm{<mi>\; </mi>}& \mathrm{<mi>\; </mi>}& \mathrm{<mi>\; </mi>}& 0\\ & & & \end{array}\right)\mathrm{,}$ (14)

where $H\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo><mo\; stretchy="false">(</mo>}d\Omega \mathrm{<mo>/</mo>}d\tau \mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}\Omega \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}$ . The lower half is omitted because it is obvious due to antisymmetry of the spin form. From (14) and the surface form, we can obtain the classical Hamiltonian as²²

${ℌ}_{\text{FLRW}}\mathrm{<mo>=</mo>}-\frac{1}{2}{\mathfrak{w}}_{\mathrm{<mi>\; </mi>}\ast }^{\cdot }\wedge {\mathfrak{w}}^{\ast \cdot }\wedge {\mathfrak{S}}_{\cdot \cdot }\mathrm{<mo>=</mo>}{\Omega }^2\left[3H^2-{\left(\frac{f}{r}\right)}^2\right]\mathrm{<mi>\; </mi>}d\tau \wedge \frac{dr}{f}\wedge \mathrm{<mo\; stretchy="false">(</mo>}rd\theta \mathrm{<mo\; stretchy="false">)</mo>}\wedge \mathrm{<mo\; stretchy="false">(</mo>}r\sin \theta d\varphi \mathrm{<mo\; stretchy="false">)</mo>,}$ (15)

and the Liouville form as

$\frac{1}{2}{\mathfrak{w}}^{\cdot \cdot }\wedge {\mathfrak{S}}_{\cdot \cdot }\mathrm{<mo>=</mo>}{\Omega }^2\mathrm{<mo\; stretchy="false">[</mo>}-\frac{\cot \theta }{r}\mathrm{<mi>\; </mi>}d\tau \wedge \frac{dr}{f}\wedge \mathrm{<mo\; stretchy="false">(</mo>}r\sin \theta d\varphi \mathrm{<mo\; stretchy="false">)</mo>}$

$\mathrm{<mi>\; </mi>}+\frac{2f}{r}\mathrm{<mi>\; </mi>}d\tau \wedge \mathrm{<mo\; stretchy="false">(</mo>}rd\theta \mathrm{<mo\; stretchy="false">)</mo>}\wedge \mathrm{<mo\; stretchy="false">(</mo>}r\sin \theta d\varphi \mathrm{<mo\; stretchy="false">)</mo>}+3H\mathrm{<mi>\; </mi>}\frac{dr}{f}\wedge \mathrm{<mo\; stretchy="false">(</mo>}rd\theta \mathrm{<mo\; stretchy="false">)</mo>}\wedge \mathrm{<mo\; stretchy="false">(</mo>}r\sin \theta d\varphi \mathrm{<mo\; stretchy="false">)</mo><mo\; stretchy="false">]</mo>.}$ (16)

A canonical quantization of general relativity requires the commutation relation between the spin form and surface from as²²

$\left[{\widehat{\mathfrak{w}}}^{a_1{a}_2}\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>,}{\widehat{\mathfrak{S}}}_{b_1{b}_2}\mathrm{<mo\; stretchy="false">(</mo>}y\mathrm{<mo\; stretchy="false">)</mo>}\right]\mathrm{<mo>=</mo>}-i\hslash G{\delta }^{\mathrm{<mo\; stretchy="false">(</mo>4<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}x-y\mathrm{<mo\; stretchy="false">)</mo>}{\delta }_{b_1}^{\mathrm{<mo\; stretchy="false">[</mo>}{a}_1}{\delta }_{b_2}^{a_2\mathrm{<mo\; stretchy="false">]</mo>}}\mathrm{,}$ (17)

and otherwise zero, where ${\delta }_{b_1}^{\mathrm{<mo\; stretchy="false">[</mo>}{a}_1}{\delta }_{b_2}^{a_2\mathrm{<mo\; stretchy="false">]</mo>}}\mathrm{<mo>=</mo>}{\delta }_{b_1}^{a_1}{\delta }_{b_2}^{a_2}-{\delta }_{b_1}^{a_2}{\delta }_{b_2}^{a_1}$ . Here, ${\widehat{\mathfrak{w}}}^{••}$ and ${\widehat{\mathfrak{S}}}_{••}$ are operators respectively corresponding to the spin and surface forms, which are formally described as

$\{\begin{array}{cc}{\widehat{\mathfrak{w}}}^{••}& \mathrm{<mo>=</mo>}{\mathfrak{w}}^{••}\mathrm{,}\\ {\widehat{\mathfrak{S}}}_{••}& \mathrm{<mo>=</mo>}i\hslash G\frac{\delta \mathrm{<mi>\; </mi><mi>\; </mi>}}{\delta {\mathfrak{w}}^{••}}\mathrm{.}\end{array}$ (18)

The commutation relation (17) can be represented using terms of the FLRM metric. The metric tensor is a functional of two functions $\Omega \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}$ and $f\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>}$ other than the integration measure. On the other hand, the Liouville–form (16) includes a derivative $\dot{\Omega }$ , and it does not have a term $df\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}dr$ . Therefore, quantization of the system can be performed by replacing a scale faction $\Omega$ by the corresponding operator as $\widehat{\Omega }$ . The conformal–time derivative¹ $\dot{\Omega }\mathrm{<mo>=</mo>}d\Omega \mathrm{<mo>/</mo>}d\tau$ is included only in the last term of (16). Thus, a non–zero component of the commutation relation can be obtained from (16) and (17) as

$\left[{\widehat{\mathfrak{w}}}^{\cdot \cdot }\mathrm{<mo\; stretchy="false">(</mo>}r\mathrm{<mo\; stretchy="false">)</mo>,}{\widehat{\mathfrak{S}}}_{\cdot \cdot }\mathrm{<mo\; stretchy="false">(</mo>}{r}^{\prime }\mathrm{<mo\; stretchy="false">)</mo>}\right]{\mathrm{<mo>|</mo>}}_{\tau \mathrm{<mo>=</mo>}{\tau }^{\prime }}\mathrm{<mo>=</mo>2}\cdot 3\left[\widehat{\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\dot{\Omega }}\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}\right]d^{3}r\mathrm{<mo>\text{'}</mo>}$ (19)

where $r\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}\tau \mathrm{,}r\mathrm{<mo\; stretchy="false">)</mo>}$ , $r^{\prime }\mathrm{<mo>=</mo><mo\; stretchy="false">(</mo>}{\tau }^{\prime }\mathrm{,}r\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>}$ and $r$ , $r\mathrm{<mo>\text{'}</mo>}$ are three–dimensional spacial vectors. The three–dimensional integration can be expressed as

$d^{3}r\mathrm{<mo>\text{'}</mo><mo>=</mo>}\frac{d{r}^{\prime }}{f\mathrm{<mo\; stretchy="false">(</mo>}{r}^{\prime }\mathrm{<mo\; stretchy="false">)</mo>}}\wedge \mathrm{<mo\; stretchy="false">(</mo>}{r}^{\prime }d\theta \mathrm{<mo\; stretchy="false">)</mo>}\wedge \mathrm{<mo\; stretchy="false">(</mo>}{r}^{\prime }\sin \theta d\varphi \mathrm{<mo\; stretchy="false">)</mo>.}$ (20)

On the other hand, the tight hand side of (17) is represented as

$\mathrm{<mo\; stretchy="false">(</mo>17<mo\; stretchy="false">)</mo><mo>=</mo>}-i\mathrm{<mo\; stretchy="false">(</mo>2}\hslash G\mathrm{<mo\; stretchy="false">)</mo>}{\delta }^3\mathrm{<mo\; stretchy="false">(</mo>}r-r\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>.}$ (21)

Therefore, the commutation relation is obtained as

$\left[\widehat{\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\dot{\Omega }}\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}\right]d^{3}r\mathrm{<mo>\text{'}</mo><mo>=</mo>}-i\frac{\hslash G}{3}{\delta }^3\mathrm{<mo\; stretchy="false">(</mo>}r-r\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>.}$ (22)

This can be understood as the equal–time commutation relation of the conformal metric. While this commutation relation is obtained from the commutation relation (17), one can obtain the same result based on quantization by Nakanishi²⁸ as shown in Appendix A.

The scalar field can be defined in the conformal metric with $K\mathrm{<mo>=</mo>0}$ in the Cartesian coordinate for three–dimensional space

$d{s}^2\mathrm{<mo>=</mo>}{\Omega }^2\left(\tau \right)\left(d{\tau }^2-{\left(d{x}^1\right)}^2-{\left(d{x}^2\right)}^2-{\left(d{x}^3\right)}^2\right)$ (23)

Instead of a polar–coordinate because virbeins are now independent of $r$ . The action integral of a scalar Lagrangian (9) in the conformal FLRW metric can be obtained as²⁹

${ℐ}_s\mathrm{<mo>=</mo>}{\displaystyle \int }{\mathfrak{L}}_S\mathrm{<mo>=</mo>}{\displaystyle \int }d\tau \wedge d{x}^1\wedge d{x}^2\wedge d{x}^3\left[\frac{1}{2}{\eta }^{\cdot \cdot }\left({\partial }_{\cdot }\chi \right)\left({\partial }_{\cdot }\chi \right)+\frac{1}{2}\frac{\ddot{\Omega }}{\Omega }{\chi }^2-V\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo>}\right]$ (24)

using a local conformal coordinate, where $\chi \mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}\phi \mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}$ . We note that $\sqrt{-det\mathrm{<mo>\{</mo>}{g}_{••}\mathrm{<mo>\}</mo>}}\mathrm{<mo>=</mo>}{\Omega }^4$ for the conformal metric (23). For further discussions, we specify the potential energy as the Higgs–type field as;

$V\left(\chi \right)\mathrm{<mo>=</mo>}{\Omega }^{4}V\mathrm{<mo\; stretchy="false">(</mo>}\phi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\frac{1}{2}{\left(\Omega \frac{\mu }{\hslash }\right)}^2{\chi }^2+\frac{\lambda }{4}{\chi }^4\mathrm{,}$ (25)

where $\mu$ and $\lambda \mathrm{<mo>></mo>0}$ is real constants. Here the physical dimension of each term is given as;

$\left[\mu \right]\mathrm{<mo>=</mo>}M\mathrm{,<mi>\; </mi>}\left[\hslash \right]\mathrm{<mo>=</mo>}LM\to \left[\frac{\mu }{\hslash }\right]\mathrm{<mo>=</mo>}{L}^{-1}\mathrm{,<mi>\; </mi>}\left[\frac{\Omega \mu }{\hslash }\chi \right]\mathrm{<mo>=</mo>}{L}^{-2}\mathrm{.}$ (26)

This field $\chi$ is provided owing to scale the scalar field $\phi$ by the conformal function $\Omega \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}$ , which is referred to as the scaled scalar field (SSF). While a quartic term has no corrections, a quadratic term receives corrections from the conformal function and its second derivative. According to a standard procedure for field quantization (canonical quantization), the field and its conjugate momentum are replaced by corresponding operators. Here, the non–zero component of equal–time commutation relations of the SSF are naturally introduced from (21) as;

$\left[\widehat{\chi }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{,}x\mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\dot{\chi }}\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{,}x\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>}\right]\mathrm{<mo>=</mo>}\widehat{\phi }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{,}x\mathrm{<mo\; stretchy="false">)</mo>}\widehat{\phi }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{,}x\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>}\left[\widehat{\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>,}\widehat{\dot{\Omega }}\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}\right]\mathrm{,}$

$\mathrm{<mo>=</mo>}i\frac{\hslash G}{3}|\widehat{\phi }\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}{|}^2{\delta }^{\mathrm{<mo\; stretchy="false">(</mo>3<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}x-x\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>}\to i{\delta }^{\mathrm{<mo\; stretchy="false">(</mo>3<mo\; stretchy="false">)</mo>}}\mathrm{<mo\; stretchy="false">(</mo>}x-x\mathrm{<mo>\text{'}</mo><mo\; stretchy="false">)</mo>,}$ (27)

where $\widehat{\phi }\mathrm{<mo\; stretchy="false">(</mo>}x\mathrm{<mo\; stretchy="false">)</mo>}$ is a scaler field operator. The overall factor $\hslash G\mathrm{<mo>/</mo>3}$ can absorbed by re–definition of the scalar field. Although the $\widehat{\phi }$ is an operator, it is assumed to commutes each other as $\mathrm{<mo\; stretchy="false">[</mo>}\widehat{\phi }\mathrm{,}\widehat{\dot{\phi }}\mathrm{<mo\; stretchy="false">]</mo><mo>=</mo>0}$ . Non–commutativity of $\chi$ and $\dot{\chi }$ is induced by that of $\Omega$ and $\dot{\Omega }$ .

Since the commutation relation (27) for the scaled–field operator $\widehat{\chi }$ is the same as the standard Klein–Gordon field–operator, the standard procedure of the field quantization in a momentum space using the Fock Hilbert–space can be performed as usual. We note that, in the SSF formalism, the commutation relation is required only on the space–time metric (vierbein). Any observers in the local space time cannot observe the scalar field independently form the space time metric. This is one of a realization of the concept given in Kurihara³⁰ such that “Classical mechanics in the stochastic space is equivalent to quantum mechanics on the standard space time manifold”. According to this concept, only the vierbein is quantized using the quantum commutation relations with keeping the scalar field classical. Even if the local observer is in the flat space–time, one may observe the SSF which is quantized due to the quantum space time. From equations (24) and (25), the effective potential can be obtained as;

$\tilde{V}\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}-\frac{1}{2}{\left(\frac{\tilde{\mu }}{\hslash }\right)}^2{\chi }^2+\frac{\lambda }{4}{\chi }^4\mathrm{,}$ (28)

where

${\left(\frac{\tilde{\mu }}{\hslash }\right)}^2\mathrm{<mo>=</mo>}\frac{\ddot{\Omega }}{\Omega }+{\left(\frac{\Omega \mu }{\hslash }\right)}^2\mathrm{.}$ (29)

An effective mass of the SSF has time dependence through the relation (29), and the electroweak phase–transition from unbroken to broken phases can occur through it. Although the SSF mass was very small, which corresponds to the unbroken phase, owing to a small value of $\Omega$ and $\ddot{\Omega }\mathrm{<mo>/</mo>}\Omega$ at the early universe, it can be large as the same as that in the current universe after the inflation due to the second term with a large value of $\Omega$ . In the current universe, the first term of (29) is negligibly small compared with the second term, and the time dependence of the mass term through $\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ is much smaller than the current accuracy of Higgs mass measurements.

A vacuum expectation value $v_0\mathrm{<mo>=</mo>}\tilde{\mu }\mathrm{<mo>/</mo>}\sqrt{\lambda }$ and higgs mass $m_h\mathrm{<mo>=</mo>}\sqrt{2}\mathrm{<mi>\; </mi>}\tilde{\mu }$ can be extracted from the effective potential. The Klein–Gordon equation obtained from the action (24) with respect to the scaled field $\chi$ can be expressed as

$\ddot{\chi }-\Delta \chi +\frac{\partial \tilde{V}}{\partial \chi }\mathrm{<mo>=</mo>0,}$ (30)

where $\Delta \mathrm{<mo>=</mo>}{\displaystyle {\sum }_{i\mathrm{<mo>=</mo>1,2,3}}}{\partial }_i{\partial }_i$ . For the uniform and isotoropic universe, one can set $\Delta \chi \mathrm{<mo>=</mo>0}$ . In this case, the energy–momentum tensor (11) is represented as

$T_{00}\mathrm{<mo>=</mo>}\frac{1}{2}{\dot{\chi }}^2+\tilde{V}\mathrm{,}$ (31)

$T_{ii}\mathrm{<mo>=</mo>}\frac{1}{2}{\dot{\chi }}^2-\tilde{V}\mathrm{,<mi>\; </mi><mi>\; </mi><mi>\; </mi>}i\mathrm{<mo>=</mo>1,2,3<mi>\; </mi><mo\; stretchy="false">(</mo>}\text{not summed}\mathrm{<mo\; stretchy="false">)</mo>,}$ (32)

and other components are zero. This energy–momentum tensor can be interpreted as a density ( $\rho$ ) and pressure ( $p$ ) of a perfect fluid as $T_{00}\mathrm{<mo>=</mo>}\rho$ and $T_{ii}\mathrm{<mo>=</mo>}p$ , respectively.

¹In this work, while the conformal-time derivative is denoted by a dot as $\dot{•}\mathrm{<mo>=</mo>}d•\mathrm{<mo>/</mo>}d\tau$ , the proper-time derivative is always written explicitly as $d•\mathrm{<mo>/</mo>}dt$ .

Friedmann equation

The Einstein equation (10) for perfect fluid with the conformal metric (13) can be expressed as follows:

$\mathrm{3<mo\; stretchy="false">(</mo>}{H}^2+K\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}+\kappa \hslash \mathrm{<mi>\; </mi>}\rho \mathrm{,}$ (33)

$2\dot{H}+H^2+K\mathrm{<mo>=</mo>}-\kappa \hslash \mathrm{<mi>\; </mi>}p\mathrm{,}$ (34)

where the curvature $K$ is put buck in this subsection. These equations, refereed to as the Friedmann equations, can be rearranged as

$H^2\mathrm{<mo>=</mo>}\frac{2\kappa \hslash }{3}\rho -K\mathrm{,}$ (35)

$\dot{H}\mathrm{<mo>=</mo>}-\frac{\kappa \hslash }{3}\left(\rho +3p\right)\mathrm{.}$ (36)

When the density and pressure are provided from the SSF, the Friedmann equations have a form

$H^2\mathrm{<mo>=</mo>}+\frac{2\kappa \hslash }{3}\left(\frac{1}{2}{\dot{\chi }}^2+\tilde{V}\right)-K\mathrm{,}$ (37)

$\dot{H}\mathrm{<mo>=</mo>}-\frac{2\kappa \hslash }{3}\left({\dot{\chi }}^2-\tilde{V}\right)\mathrm{.}$ (38)

If appropriate initial conditions are given, the history of the universe can be obtained by solving equations (30), (37) and (38), simultaneously. Further simplification is possible in this case as follows: A conformal–time derivative of (37) provides a equation

$\frac{d{H}^2}{d\tau }\mathrm{<mo>=</mo>}\frac{2\kappa \hslash }{3}\left(\ddot{\chi }+\frac{\partial \tilde{V}}{\partial \chi }\right)\dot{\chi }-\frac{\kappa }{3\hslash }\frac{d{\tilde{\mu }}^2}{d\tau }{\chi }^2\mathrm{,}$

$\mathrm{<mo>=</mo>}\frac{2\kappa \hslash }{3}\Delta \chi \dot{\chi }-\frac{\kappa }{3\hslash }\frac{d{\tilde{\mu }}^2}{d\tau }{\chi }^2\mathrm{,}$ (39)

where the Klein–Gordon equation (30) is used. Under the assumption that the SSF is the uniform and isotoropic, a spacial derivative are set to zero again as $\Delta \chi \mathrm{<mo>=</mo>0}$ . Therefore, the equation (39) can be expressed as

$\frac{d{H}^2}{d\tau }\mathrm{<mo>=</mo>}-\frac{\kappa }{3\hslash }\frac{d{\tilde{\mu }}^2}{d\tau }{\chi }^2\mathrm{.}$ (40)

Due to definitions of ${\tilde{\mu }}^2$ in (29), its conformal time derivative is expressed as

$\frac{d{\tilde{\mu }}^2}{d\tau }\mathrm{<mo>=</mo>}{\hslash }^2\frac{d}{d\tau }\left(\frac{\ddot{\Omega }}{\Omega }\right)+2\Omega \dot{\Omega }{\mu }^2\mathrm{.}$ (41)

Under the assume that higher derivatives of the scale function $\Omega$ are much smaller than both the scale function itself and first derivative of that, the first term on the righthand side can be ignored compared with the second term. The validity of this assumption will be confirmed later in this section. In this case, the equation (40) can be approximated as

$\frac{\dot{\Omega }}{\Omega }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\sqrt{\frac{\kappa }{3\hslash }}\mu \mathrm{<mi>\; </mi>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}\chi \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>,}$ (42)

where $H\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo><mo>></mo>0}$ is assumed through any $\tau$ . This equation can be express using the proper time $t$ using a relation $\Omega \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}d\tau \mathrm{<mo>=</mo>}dt$ as

$\frac{d\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{dt}\mathrm{<mo>=</mo>}\sqrt{\frac{\kappa }{3\hslash }}\mu \mathrm{<mi>\; </mi>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>.}$ (43)

The second Friedmann equation (38) can be approximated under the same assumptions as

$\frac{d\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{dt}\mathrm{<mo>=</mo>}\sqrt{\frac{\kappa }{3}}{\left[\Omega {\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}^2\left(2{\left(\frac{d\chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{dt}\right)}^2+{\left(\frac{\mu }{\hslash }\chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\right)}^2\right)-\frac{\lambda }{2}\chi {\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}^4\right]}^{\frac{1}{2}}\mathrm{.}$ (44)

Above two Friemann equations (43) and (44) must be consistent each other within the approximation. It leads a following differential equation

$\dot{\chi }\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\pm \frac{\sqrt{\lambda }}{2}\chi {\mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo>}}^2\mathrm{,}$ (45)

with respect to the conformal time $\tau$ . This equation can be solved as

$\chi \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\left(\mp \frac{\sqrt{\lambda }}{2}\tau +\frac{1}{{\chi }_0}\right)}^{-1}\mathrm{,}$ (46)

where ${\chi }_0\mathrm{<mo>=</mo>}\chi \mathrm{<mo\; stretchy="false">(</mo>}\tau \mathrm{<mo>=</mo>0<mo\; stretchy="false">)</mo>}$ . This solution does not give any oscillating fields because of the requirement $\Delta \chi \mathrm{<mo>=</mo>0}$ .

Numerical calculations

Next the scaling function for the cosmic inflation era is treated in this section. During the cosmic inflation, a condition $d\Omega \mathrm{<mo>/</mo>}dt\gg d\chi \mathrm{<mo>/</mo>}dt$ is expected naturally. Due to the definition of the SSF, this condition can be satisfied if $\phi \ll 1$ and $d\phi \mathrm{<mo>/</mo>}dt\ll \mathrm{<mo\; stretchy="false">(</mo>}d\Omega \mathrm{<mo>/</mo>}dt\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}\Omega$ during the cosmic inflation. A validity of this assumption will be discussed later in this section. The Friedmann equation (43) can be solved under the assumption as;

$\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\Omega }_0\exp \left(H_{0}t\right)\mathrm{,}$ (47)

where $H_0\mathrm{<mo>=</mo>}\sqrt{\kappa \mathrm{<mo>/</mo>3}\hslash }\mathrm{<mi>\; </mi>}\mu {\chi }_0$ with an initial condition of $\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo>=</mo>0<mo\; stretchy="false">)</mo><mo>=</mo>}{\Omega }_0$ . Due to the assumption above, the SSF stays constant at $\chi \mathrm{<mo\; stretchy="false">(</mo>0<mo><</mo>}t\mathrm{<mo><</mo>}{t}_e\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}{\chi }_0$ during the inflation. An inflation starting time is set to $t\mathrm{<mo>=</mo>0}$ . An initial value of the SSF may be given by a quantum fluctuation of the field, which is naturally expected to be an order unity. Here the initial value ${\chi }_0\mathrm{<mo>=</mo>1}$ in the Planck units is assumed. On the other hand, the Higgs potential parameters, $\mu$ and $\lambda$ , at the beginning of the universe are set to be the same as the current universe at the tree level for simplicity. From the recent measurement of the Higgs mass,³¹ the quadratic term can be obtained as $\Omega \mu \mathrm{<mo>/</mo>}\hslash \mathrm{<mo>=</mo>90} GeV$ and $\lambda \mathrm{<mo>=</mo>0.134}$ . Therefore, the initial value $H_o$ is obtained in the Planck units as $H_0\mathrm{<mo>=</mo>90<mo>/</mo><mo\; stretchy="false">(</mo>}\sqrt{3}{m}_p\mathrm{<mo\; stretchy="false">)</mo>}$ , where $m_p\mathrm{<mo>=</mo>1.22}\times {10}^{19} GeV$ is the Planck mass in the natural units. In order to make the inflation scenario working well, the e–folding number $N_e$ defined as $\exp \mathrm{<mo\; stretchy="false">(</mo>}{N}_e\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\Omega \mathrm{<mo\; stretchy="false">(</mo>}{t}_e\mathrm{<mo\; stretchy="false">)</mo><mo>/</mo>}{\Omega }_0$ must be greater than or around 70. When the normalization $\Omega \mathrm{<mo\; stretchy="false">(</mo>}{t}_e\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}$ and the e–folding number $N_e\mathrm{<mo>=</mo>70}$ are required, the initial value of the scaling function can be obtained as ${\Omega }_0\mathrm{<mo>=</mo>}{e}^{-70}$ . The inflation termination–time can be obtained by solving the $\Omega \mathrm{<mo\; stretchy="false">(</mo>}{t}_e\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>1}$ such as $t_e\mathrm{<mo>=</mo>0.89}\times {10}^{-24}$ second. In our scenario, a speed of changing a vacuum expectation value was very high, and thus, the SSF vacuum is staying at the origin $V\mathrm{<mo\; stretchy="false">(</mo>}\chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo>=</mo>0<mo\; stretchy="false">)</mo><mo\; stretchy="false">)</mo><mo>=</mo>0}$ for a short period. Then, delayed explosion of the SSF field $\chi$ caught the vacuum expectation value up and the inflation was terminated. Therefore, the electroweak phase–transition must be the second kind.

The evolution of the scaling function can be fixed completely using above parameters under the approximations. Before a starting time of the inflation, the first term of (29) was much smaller than the second term. At that period, the potential energy of the SSF had a minimum at $\chi \mathrm{<mo>=</mo>0}$ as shown in Figure 1 $\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo>=</mo>0<mo\; stretchy="false">)</mo>}$ . During the inflation, the SSF had a finite vacuum expectation value (Figure 1 $\mathrm{<mo\; stretchy="false">(</mo>0<mo><</mo>}t\mathrm{<mo><</mo>}{t}_e\mathrm{<mo\; stretchy="false">)</mo>}$ ). At the end of the inflation, the vacuum expectation value arrived at the same value as that in the current universe (Figure 1 $\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo>=</mo>}{t}_e\mathrm{<mo\; stretchy="false">)</mo>}$ ). Although the vacuum expectation value stayed almost constant at the beginning inflation, it grew very rapidly after the second term of (29) became dominant in the potential energy as shown in Figure 2. The inflation was terminated when the SSF arrived at the vacuum expectation value, and it fixed the e–folding number. A precise value of the inflation ending time must be evaluated by solving equations (43) and (45) (or equivalently (46)), simultaneously. We note that the relation between the conformal and proper times can be fixed only after the solution of the scaling function is obtained. One cannot solve equations analytically without the approximation that the SFF is constant during the inflation. When the inflation duration changed $\pm \mathrm{1<mi>\%</mi>}$ around its nominal value, the e–folding number varied about $\pm 2$ as shown in Figure 3. On the other hand, the same variation for the duration of the inflation affects the vacuum expectation value about $\mathrm{50<mi>\%</mi>}$ to $\mathrm{500<mi>\%</mi>}$ , as shown in Figure 2. A tolerance of the inflation duration is rather narrow to realize a current observed value of the vacuum expectation value.

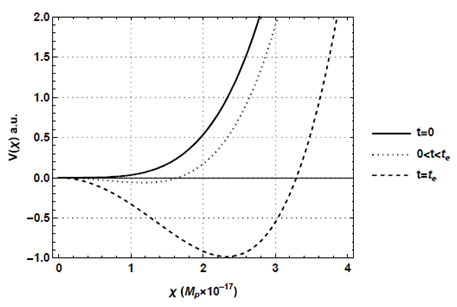
Figure 1 The potential energy of the SSF before the inflation (solid line), during the inflation (dotted line), and at the end of the inflation (dashed line).

Figure 2 The potential–energy term of the SSF normalized using the SM value in the current universe. If we require that the cosmic inflation terminated when the potential–energy term of the SSF arrived at the current value$\left(V_0=V_0\left(SM\right)=1\right)$ , a duration of the in ation is$0.89\times {10}^{-24}$ second.

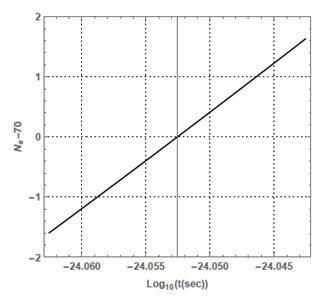
Figure 3 The e–folding number different from nominal value$N_e-70$ is shown with respect to the duration time of the ination. When the ination duration changed$\pm 1\%$ around its nominal value, the e–folding number varied about$\pm 2$ .

The solution (47) is obtained under the assumption of $d\Omega \mathrm{<mo>/</mo>}dt\gg d\chi \mathrm{<mo>/</mo>}dt$ . The validity of this assumption during the cosmic inflation must be confirmed. If the time dependence of the SSF is put back in the solution as $H_0\to H\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo><mo>=</mo>}\sqrt{\kappa \mathrm{<mo>/</mo>3}\hslash }\mathrm{<mi>\; </mi>}\mu \chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}$ , the time derivative of the scaling function becomes

$\frac{d\Omega \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{dt}\mathrm{<mo>=</mo>}{\Omega }_{0}H\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}\left(1+\frac{1}{\chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}\frac{d\chi \mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}}{dt}t\right)\exp \left(H\mathrm{<mo\; stretchy="false">(</mo>}t\mathrm{<mo\; stretchy="false">)</mo>}t\right)\mathrm{.}$ (48)

In calculations for the cosmic inflation, the time derivative term in the right hand side is neglected. The validity of this approximation can be examined using the equation of motion. The time evolution of the SSF is governed by the equation (46) with respect to the conformal time. For a conversion from the conformal time to the proper time, the approximated solution of (47) is used for a numerical calculation. A numerical result of a time evolution of the tern $\mathrm{<mo\; stretchy="false">(</mo>}d\chi \mathrm{<mo>/</mo>}dt\mathrm{<mo\; stretchy="false">)</mo>}t\mathrm{<mo>/</mo>}\chi$ is shown in Figure 4. It is shown that that term is less than unity during the cosmic inflation, and thus the effect on the result is a factor of two on ${\Omega }_0$ at most.

Figure 4 A term$\left(t/\chi \right)d\chi /dt$ is shown with respect to the inflation duration. The approximation used in this report requires a value must be small compare with unity.

We propose a novel method to treat the electroweak symmetry braking, which is named the scaled scalar–field method. In this method, a conformal metric is employed and the Higgs field is scaled owing to the conformal function. In consequence, a mass parameter of the Higgs field (a quadratic term of the Higgs potential) has the time dependence through the conformal function, and it causes the phase transition. Quantization of the Higgs field is induced associated with the canonical quantization of general relativity. In the context of the scaled field, only the vierbein is quantized owing to the quantum commutation relations with keeping the scalar field classical.
The cosmic inflation and the electroweak phase–transition are investigated in a framework of the scaled field. The Friedmann equations and their appropriate approximations are provided using the scaled field method. The Friedmann equations are numerically solved and an example of a possible solution to match with the cosmic inflation scenario is shown. The electroweak phase–transition induced by the scaled field is the second kind, and thus, the fine–tuning problem is still exists.

I appreciate the kind hospitality of all members of the theory group of Nikhef, particularly Prof. J. Vermaseren and Prof. E. Laenen. A major part of this study has been conducted during my stay at Nikhef in 2017. In addition, I would like to thank Dr. Y. Sugiyama for his continuous encouragement and fruitful discussion.

Author declares there is no conflict of interest.

1. Aad G. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Physical Letters B. 2012;716:1–29.
2. Chatrchyan C. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Physical Letters B. 2012;30(61):716.
3. Englert F, Brout R. Broken symmetry and the mass of gauge vector mesons. Physical Review Letters. 1964;13(321):323.
4. Higgs PW. Broken symmetries and the masses of gauge bosons. Physical Review Letters. 1964;13:508–509.
5. Guralnik GS, Hagen CR, Kibble TWB. Global conservation laws and massless particles. Physical Review Letters. 1964;13:585:587.
6. Starobinsky AA. Spectrum of relict gravitational radiation and the early state of the universe. JETP Letter. 1979;30:682–685.
7. Sato K. First Order Phase Transition of a Vacuum and Expansion of the Universe. Monthly Notices of the Royal Astronomical Society. 1981;195(1981):467–479.
8. Kazanas D. Dynamics of the Universe and Spontaneous Symmetry Breaking. The Astrophysical Journal. 1980;241:L59–L63.
9. Starobinsky A. A new type of isotropic cosmological models without singularity. Physics Letters B. 1980;91(1):99–102.
10. Mukhanov VF, Chibisov G. Quantum uctuations and a nonsingular universe. JETP Letters. 1981;33(10):532–535.
11. Guth AH. Inationary universe: A possible solution to the horizon and atness problems. Physical Review D. 1981;23:347–356.
12. Linde A. A new inationary universe scenario: A possible solution of the horizon, atness, homogeneity,isotropy and primordial monopole problems. Physics Letters B. 1982;108(6):389–393.
13. Linde A. Chaotic ination. Physics Letters B. 1983;129(3):177–181.
14. Bezrukov F, Shaposhnikov M. The standard model higgs boson as the inaton. Physics Letters B. 2008;59(3):703–706.
15. Coleman S, Weinberg E. Radiative corrections as the origin of spontaneous symmetry breaking. Physical Review D. 1973;7:1888–1910.
16. Foot R. Kobakhidze A, Volkas R. Electroweak higgs as a pseudo–goldstone boson of broken scale invariance. Physics Letters B. 2007;655(3):156–161.
17. Meissner KA, Nicolai H. Conformal symmetry and the standard model. Physics Letters B. 2007;648(4):312–317.
18. Holthausen M, Lindner M, Schmidt MA. Radiative symmetry breaking of the minimal left–right symmetric model. Physical Review D. 2010;82:055002.
19. Satoshi Iso, Pasquale D Serpico, Kengo Shimada. Qcd–electroweak first–order phase transition in a supercooled universe. Physical Review Letters. 2017;119:141–301.
20. Iso S, Okada N, Orikasa Y. Classically conformal b–l extended standard model. Physics Letters B. 2009;76(1):81–87.
21. Kurihara Y. Geometrothermodynamics for Black holes and de Sitter Space. General Relativity and Gravity. 2018;50(2).
22. Kurihara Y. General relativity as the four dimensional Chern–Weil theory. USA: Cornell University Library; 2017.
23. Kurihara Y. Compact four–dimensional euclidean space embedded in the universe. Physics & Astronomy International Journal. 2018;2(3):237–241.
24. Einstein A. Bemerkung zu der Arbeit von A. Friedmann “Über die Krümmung des Raumes”. Zeitschrift für Physik. 1922;11(1):326.
25. Lemaitre G. L'univers en expansion. Annals of the Scientific Society of Brussels. 1927;A47:49–59.
26. Robertson HP. Kinematics and World–Structure. The Astrophysical Journal. 1935;82:284.
27. Walker AG. On milne's theory of world–structure. Proceedings of the London Mathematical Society. 1937;s2–42(1):90–127.
28. Nakanishi N. Indefinite Metric Quantum Field Theory of General Relativity. VI: Commutation Relations in the Vierbein Formalism. Progress of Theoretical Physics. 1979;62(4):1101–1111.
29. Mukhanov V, Winitzki S. Introduction to Quantum Effects in Gravity. UK: Cambridge University Press; 2007.
30. Kurihara Y. Stochastic metric space and quantum mechanics. Journal of Physics Communications. 2018;2(3)1–33.
31. Patrignani C, Agashe K, Aielli G, et al. Review of Particle Physics. Chinese Physics C. 2016;40(10):1–1809.