The paper considers a hypothesis of the structure of ball lightning core as an ensemble of dynamic electric capacitors. The dynamic capacitor is an object consisting of spatially separated charges – electrons and protons. Electrons, due to the action of mutually orthogonal electric and magnetic fields, move in a circle, oscillating in the radial direction. The magnetic field is generated by the movement of protons around the electron ring. The number of protons exceeds the number of electrons, due to which the dynamic capacitor has a positive electric charge. The system of dynamic capacitors is located inside a spherical shell consisting of water molecules polarized in the electric field of the charge of the dynamic capacitor. The shell creates a force that prevents the expansion of dynamic capacitors. It is shown that 1900 dynamic capacitors with a radius of 0.5 cm with a total kinetic energy of 6.36 MJ can fit in ball lightning with an internal shell radius of 6.2 cm. In this case, the energy density in the core of ball lightning can be about 6.4·10⁹ J/m³. This is comparable with the result of measurements of energy density of natural ball lightning.

Keywords: Ball lightning; Movement of electrons and ions in an electric and magnetic field; Dynamic electric capacitor.

The principle of the dynamic electric capacitor

In a series of articles describing the properties of ball lightning, we discussed the possibility of existence of two types of ball lightning: 1) with a low-activity core of stationary ions and 2) with a core of moving ions and electrons (systems of “dynamic electric capacitors”).^1-5 The study of the structure of ball lightning possessing an energetically active core is of great interest, since they are objects with a high energy density ρ_E = 10¹⁰ J/m³ and higher.⁶ The construction of a model of ball lightning usually begins with determining the principle of its structure. In 1859, de Tessan, a member of the French Academy of Sciences, proposed the idea of ​​​​a ball lightning device in the form of an electric capacitor made of two charged coaxial spheres, between which there is an insulator - compressed air.⁷ Let the radius of the outer sphere be R_out = 10 cm and the radius of the inner sphere be R_in = 9 cm. The capacitance of such a capacitor is C = 4πε₀ε/(R_in^-1 – R_out^-1). (Here ε₀ = 8.854·10^-12 F/m is the electric constant and ε is the permittivity of the insulator material). Substituting ε = 1 and the numerical values ​​of R_in and R_out into this expression, we find C = 1.23·10^-10 F. Taking the value of the electric field strength between the electrodes equal to the breakdown strength of air E_bra = 3·10⁶ V/m, we find the potential difference between the electrodes U = E_bra (R_out – R_in) = 3·10⁴ V and the energy stored in the capacitor, W_e = CU²/2 = 5.53·10^-2 J. The energy can be increased in two ways. The voltage between the electrodes can be raised. In this case, with a 10-fold increase in voltage, the energy will increase 100-fold. The limit to voltage growth is set by the electrical strength of the gap between the electrodes. It can be increased by creating a high vacuum in the gap or filling it with a dielectric with high electrical strength. Currently, the electrical strength of the best insulators does not exceed U_brd = 10⁹ V/m. Substituting this value and ε = 2.5 into the expression for energy, we find W_ed = 1.54·10⁴ J. As we can see, the energy stored in the capacitor has increased by 3·10⁵ times, but its value is still 10³-10⁵ times less than the measured values ​​of the energy of ball lightning.⁶ The second method is the accumulation of energy not in the form of stretched molecular bonds, as in the case considered, but in the form of the kinetic energy of particles. In⁸ the device of a “hydromagnetic capacitor” is described, which is a plasma rotating in an axial magnetic field H. In this capacitor the charges are spatially separated: positive ions move along an orbit of large radius, and electrons move along an orbit of small radius. The linear velocity of plasma rotation v_θ = E/μ₀H, where μ₀ = 1.2566·10^-6 V·s/A·m is the magnetic constant, and E is the electric field strength in the space between the regions of positive and negative charges. Due to the rotation of the plasma, the kinetic energy of a unit volume W_k = ρv_θ²/2 (ρ is the plasma density) is added to the energy of the electric field stored in a unit volume of the capacitor, W_e = ε₀E²/2.

To some extent we are the successors of the ideas of ​​de Tessan and the authors of the hydromagnetic capacitor. Taking the device of a “hydromagnetic capacitor” as a basis, we will present a diagram of charges movement, when the radial electric field and axial magnetic field are created due to the proper movement of electrons and protons (Figure 1).^9-11 For simplicity of presentation, we will assume that the orbits of protons and electrons lie in the same plane.

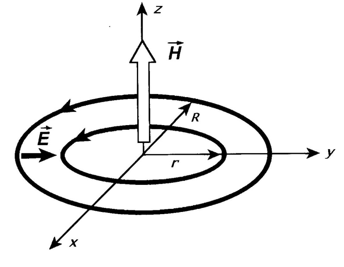
Figure 1 Scheme of charges movement in a dynamic electric capacitor. The inner ring is formed by electrons, and the outer one by protons. The magnetic field H is generated by rotating protons, the electric field E creates a centripetal force that holds the protons in orbit.

Protons (outer ring) move along an orbit of radius R under conditions of equality of the centrifugal force and the Coulomb force of their attraction to the electron ring of radius r. Due to the rotation of the protons, a magnetic field H is generated inside the orbit, the vector of which has a component perpendicular to the plane of the orbit. We will assume that the protons rotate counterclockwise, therefore the magnetic field they create will be directed upward from the XY plane. Under the action of this field and the orthogonal electric field E, existing in the space between the electron and proton rings, the electrons drift in the direction of the vector product of E and H (that is, they also move counterclockwise) with a velocity:^12,13

v_d = [E·H] /μ₀H²,                                       (1)          

For a sufficiently strong magnetic field, determined from the condition:¹⁴

H ≥ (ε₀/μ₀)^1/2E,                                 (2)

the drift of electrons in the direction opposite to the vector E will be suppressed, and they will move (at a speed close to the speed of light) in a circular orbit of radius r, while performing radial oscillations with an amplitude of:¹⁵

Δr = (2mE) / (eμ₀²H²).                       (3)

Here m is the electron mass and e is its charge. The amplitude Δr  must be less than the distance between the electron and proton orbits: Δr < R – r. In the considered dynamic capacitor, in which protons move along an orbit due to the centripetal force created by the charge of the electron ring, and electrons drift along a closed orbit, there is no need for material charge carriers such as metal electrodes of the capacitor. Moreover, the presence of such electrodes could cause autoelectronic emission of charges already at an electric field strength of E = 10⁸ V/m, which would significantly limit the energy capabilities of our capacitor.¹⁶

Let us analyze how to ensure the stability of electron motion in the plane of the electron ring. Figure 2a shows the type of magnetic field lines created by a flat current loop (protons rotating along a flat orbit). The protons rotate clockwise, the magnetic field in the center of the coil is directed along the Z axis. In Figure 2a) it is seen that the component H_r of the magnetic field created by the proton ring is positive inside the proton orbit at z > 0 (i.e. the component of the magnetic field vector H_r is directed radially outward from the center of the ring) and negative at z < 0. If an electron moving counterclockwise with a velocity v along an orbit lying in the XY plane exits the orbital plane, then the Lorentz force F = – eμ₀ [v·H_r] directed along the Z axis will act on it, which will take it even further from the orbital plane. The same will happen with an electron displaced in the opposite direction of the Z axis. In order for the electrons that exited the orbital plane to return back, the signs of H_r must be opposite to those considered.

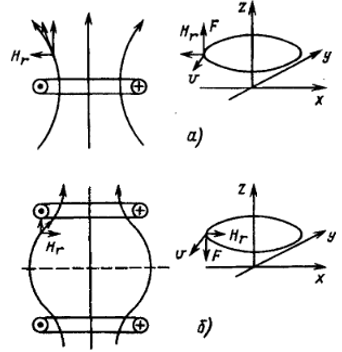
Figure 2. Forces acting on electrons in a magnetic field created by the motion of protons. a) On the left – lines of force of the magnetic field created by a flat current loop. On the right – type of forces acting on the electron ring located above the plane of the current loop. b) On the left – lines of force of the magnetic field created by two loops with current. On the right – type of forces acting on the electron ring located above the plane equidistant from the current rings.

The magnetic field of the required configuration can be obtained using two coaxial current rings of the same radius, spaced along the Z axis at a distance z > R (see Figure 2b). In this case, near a plane equidistant from the planes of both rings, the radial component of the magnetic field H_r, found by summing the magnetic field strengths of two turns, turns out to be negative when an electron leaves the central plane upward and positive when it shifts in the opposite direction. Therefore, the Lorentz force will return the electrons to the specified plane.

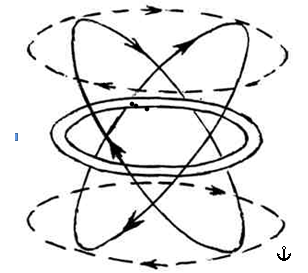
Figure 3 Scheme of orbital motion of protons in the electric field created by the electron ring. The motion of protons generates a magnetic field equivalent to the current of two coils with current.

The considered principle of axial focusing of charged particle orbits in a “barrel-shaped” magnetic field has been known for a long time and is used in cyclotrons and betatrons.^17,18 It is also known from the theory of betatrons that it is possible to stabilize the radius of the electron orbit if the rate of decrease in the axial magnetic field strength along the radius H_z(r) = const/rⁿ is less than the rate determined by the formula H_z’(r) = const/r, that is, if the condition n < 1 is met.

The proton orbits, unlike the electron orbits, will not lie in the XY plane. Due to Coulomb repulsion, the protons will most likely leave this plane and will move along numerous orbits inclined at different angles to the XY plane (Figure 3). In this case, the magnetic fields arising from the movement of the protons along the Z axis will mutually compensate each other and only the field caused by the azimuthal movement of the protons will remain. This field is equivalent to the field created by two current coils spaced apart along the axis. Thus, our system will resemble a sphere with cut poles, filled with proton orbits, inside which electrons move in a ring. This system is close to the configuration of a cylindrical capacitor.

Properties of a dynamic electric capacitor

Let us consider a cylindrical capacitor with an outer electrode of radius R = 0.5 cm, an inner electrode of radius r = 0.35 cm, and a height of h = 0.5 cm. The capacitance of such a capacitor is C = 2πε₀h/ln(R/r) = 0.78·10^-12 F. Let such a capacitor contain electric field energy W_e = 100 J. In this case, the potential difference across its electrodes is U = (2W_e/C)^1/2 = 1.6·10⁷ V, and its charge is Q = CU = 1.25·10^-5 C. The electric field strength in the gap between the electrodes, E = U/(R – r) = 1.0710¹⁰ V/m, significantly exceeds the air breakdown field (E_bra = 3·10⁶ V/m), so there must be a deep vacuum in the space between the electrodes. Equating the force F_e = eE acting on a proton in an electric field E to the centrifugal force F_c = m_pv_p²/R, we find the speed of its orbital motion v_p = 7.15·10⁷ m/s and the frequency of its revolution in orbit f_p = v_p/2πR = 2.28·10⁹ s^-1. (Here m_p = 1.673·10^-27 kg is the mass of the proton). Let us assume that our system is electrically neutral, that is, the total charge of electrons Q_e = 1.25·10^-5 C is equal to the total charge of protons Q’_p. In this case, the current created by the movement of protons will be equal to I’_p = Q’_p f_p = 2.85·10⁴ A, and the magnetic field strength at the center of the orbit created by this current will be equal to H’ = I’_p / 2R = 2.85·10⁶ A/m. To prevent radial motion of electrons in the field E, the condition H ≥ (ε₀/μ₀)^1/2E = 2.654·10^-3E must be met.¹¹ For an electric field strength E = 1.07·10¹⁰ V/m, this condition means that H ≥ 2.84·10⁷ A/m must be. As we can see, this value is an order of magnitude greater than the value of H’ that we found. To create a current that will keep the electrons in orbit, it is necessary to increase the number of protons by 10 times, that is, to increase their total charge to Q_p = 1.25·10^-4 C. Due to this, the system under consideration will have an excess positive charge Q = Q_p – Q_e =  1.125·10^-4 C. With an electric field strength of E = 1.07·10¹⁰ V/m and a magnetic field strength of H = 2.84·10⁷ A/m, the amplitude of radial oscillations of electrons will be Δr = 2mE/eμ₀²H² = 10^-2 cm, which is 15 times less than the distance between the electron and proton orbits. The kinetic energy of protons in a dynamic electric capacitor is W_p = Q_pm_pv_p²/2e = 3.34 kJ, which exceeds We by 33.4 times.

Based on the simple analysis presented, two important conclusions can be made: 1) in a dynamic electric capacitor, the number of protons exceeds the number of electrons, i.e. it has an uncompensated positive charge; 2) the energy in a dynamic capacitor is stored in the form of the kinetic energy of protons.

Now let us return to the discussion of the problem of how to hold the expanding system of moving charges under consideration in a limited volume. The expansion of proton orbits could, in principle, be restrained by the attraction of electrons if the latter, in turn, were held in orbit by a “rigid” external magnetic field. But since the magnetic field in which the electrons move is created by a proton ring capable of expansion, this field also turns out to be “non-rigid”. Therefore, to ensure the existence of our system, other forces must be present in it which prevent its expansion. For example, such a force could be the force of atmospheric pressure acting on the shell inside which the system of moving charges is located. We have long been tacitly assuming the existence of a certain shell separating the vacuum cavity in which the charges move from the atmosphere. This shell most likely consists of water molecules. Paradoxically, it is the presence of an uncompensated charge, which would seem to only aggravate the problem of particle retention (since the Coulomb repulsion force of like charges is added to the centrifugal force), that allows the existence of an object capable of providing compression of the energy core of a dynamic capacitor.

Ball lightning model with an active energy core

Let us consider a spherical shell with an internal radius R = 6.2 cm and a wall thickness a, inside which there is an energy core with a positive charge Q. This charge creates an electric field of intensity E = Q/4πε₀R² at the location of the shell. Under the influence of this field, polarization of water molecules will occur: negative charges will appear on the inner side of the shell, and positive charges on the outer side. It can be assumed that with complete polarization of the shell in a strong field, the surface charge density σ will be proportional to N_s – the number of water molecules per unit area of ​​the shell. The distance between water molecules in an ice crystal is 3·10^-10 m. Consequently, there are N_s = 10¹⁹ water molecules per square meter. The water molecule has an electric dipole moment p_w = 6.327·10^-30 C·m, and the distance d between the oxygen atom and the plane in which the hydrogen atoms are located is 0.588·10^-10 m. Thus, the molecule can be considered a dipole of length d, at the ends of which are charges q_d = p_w/d =   10^-19 C. The total charge of the ends of the dipoles on an area of ​​1 m² is equal to σ = q_d · N_s = 1 C/m². The dipole moment of a unit area of ​​a shell of thickness a is equal to D = σ·a = a C/m. The force with which a unit area of ​​the shell is attracted to a charge Q is equal to P_cp = D·grad E = – 2DQ/4πε₀R³ = – 2DE/R. The force F_cp, which pulls the shell toward the center, is found by multiplying P_cp by the shell area S = 4πR²: F_cp = (2DE/R)·( 4πR²) = 2σaQ/ε₀R. If the inner radius of the shell is R = 6.2 cm, the charge of the energetic core is Q = 10^-2 C, and the shell thickness is a = 1 cm, then the force pulling it together is equal to F_cp = 3.64·10⁸ N. Let us assume that this force compensates for the centrifugal force F_cp = M_pv_p²/R of protons with a total mass M_p, moving in an orbit with a radius of R = 6.2 cm at a velocity v_p. In this case, the kinetic energy of the protons is W_p = M_pv_p²/2 = F_cp·R/2 = 11.3 MJ. Thus, we come to the conclusion that the dielectric shell, inside which there is an electric charge, due to the force caused by the gradient of the electric field strength, is capable of resisting the expansion of the core of ball lightning, which has the energy of ten MJ.

Let us note that the shell is also acted upon by forces stretching it in the direction of the sphere radius. Indeed, the inner surface of the shell lined with the negative ends of the charges is acted upon by a force directed toward the center of the sphere, while the outer surface filled with positive charges is acted upon by a force tending to tear the shell. The force directed toward the center of the sphere is compensated by the pressure force of the expanding core of the ball lightning, whereas the force acting on the outer surface of the shell can only be compensated by the force of mutual attraction of the liquid molecules. In the case under consideration, the shell with an inner radius of R = 6.2 cm is stretched by a force of F_cp = 3.64·10⁸ N. The negative pressure of this force is P_cp = 7.5·10⁹ N/m² = 7.5·10⁴ atm. The pressure on the water surface caused by the mutual attraction of molecules is P_mol = 1.7·10⁴ atm.¹⁹ It can be expected that in a shell of water molecules polarized in a strong electric field, the value of the molecular pressure on the water surface will be somewhat greater than 1.7·10⁴ atm. Nevertheless, the limitation of the tensile strength of the shell may be one of the reasons for the existence of a limit on the energy of ball lightning.

The system we have constructed has unusual thermodynamic properties. Despite the fact that it has high energy, it is highly ordered and, therefore, its entropy can be quite low. If we understand the entropy S as a function of the logarithm of the number of states N occupied by the system: S = k_B ln N (k_B is the Boltzmann constant), we can see that the system of moving charges, firstly, occupies an insignificant part of the volume of the shell cavity (the movement of electrons and protons occurs along certain orbits, and the rest of the space is free of matter), and, secondly, the spectra of admissible values ​​of the energies of electrons and protons are also quite narrow.²⁰ In addition, the temperature of the system T = dW/dS (W is the energy of the system), which characterizes the degree of chaos of the particle motion, is low. If the movement of charge carriers occurs without collisions and the charges are uniformly distributed along the length of the orbit, then the temperature T can be noticeably lower than room temperature. A similar situation occurs in supersonic gas flows, in which, despite the high speed of movement of molecules along the jet axis, the speed of their chaotic movement in the direction perpendicular to the axis is small and is characterized by a low temperature.²¹

The above circumstances (ordering, absence of collisions, low temperature) are decisive for the process of reflection of dynamic electric capacitors, forming the energetic core of ball lightning, at the shell wall. Since at the moment of reflection the velocity of the orbital motion of the proton is directed almost tangentially to the shell, only the component of the proton momentum, caused by the expansion of the proton orbit in the radial direction, acts on it. The value of this fraction of the momentum is many orders of magnitude less than the total momentum of the proton. However, the value of the transferred momentum cannot exceed a fixed value of a large, but still finite quantity determined by the total mass of the protons, their velocity, orbital radii and Coulomb repulsion of charges. In contrast, long-term retention of a disordered system of particles (for example, chaotically moving charges) inside the shell is, in principle, impossible. Indeed, among these charges there will always be a small fraction of very fast particles, collisions with which the shell will not withstand. Moreover, due to the conservation of the Maxwellian distribution of particle velocities in the system, the loss of these fast particles will be constantly replenished.

According to the model under consideration, ball lightning may look like the one shown in Figure 4.

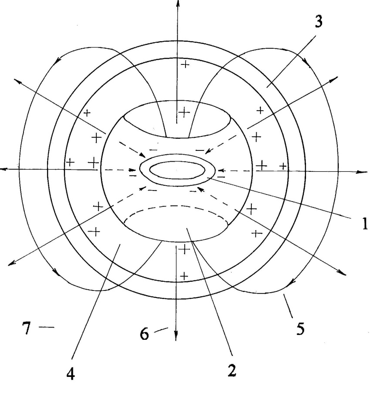
Figure 4 The structure of ball lightning with a single-element energy core: 1 – electron ring, 2 – protons, 3 – shell, 4 – vacuum, 5 – magnetic field, 6 – electric field, 7 – atmosphere.

Inside the spherical shell there is an energy core in the form of a single dynamic electric capacitor, represented by a combination of the geometric place of proton orbits (a sphere with cut poles) and an internal electron ring. This system manifests itself in the external environment by the presence of an electric field (in the form of an electric monopole) and a magnetic field (in the form of a magnetic dipole). The configuration shown in Fig. 5 is also possible, when inside the shell there is an energy core consisting of a large number of small dynamic capacitors. For example, in a shell with an internal radius R_en = 6.2 cm it is possible to place N = (R_en/R_c)³ = 1900 capacitors with a radius R_c = 0.5 cm (the characteristics of which we have considered above). The total electrical energy of these capacitors will be W_eΣ = W_e N = 190 kJ, the kinetic energy of protons W_pΣ = 6.36 MJ, and the total uncompensated charge Q_Σ = 2.14·10^-1 C. In ball lightning with a multi-element core, the magnetic fields of individual elements will most likely close on each other, and in external space it will manifest itself only as an electric monopole.

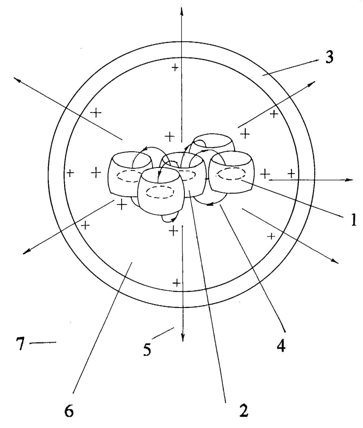
Figure 5 The structure of ball lightning with a multi-element energy core: 1 – electron ring, 2 – protons, 3 – shell, 4 – magnetic field, 5 – electric field, 6 – vacuum, 7 – atmosphere. Only a small part of the dynamic capacitors is shown. In fact, the internal cavity of the shell is densely filled with these objects.

According to the above, the core of ball lightning, which has a large energy reserve, has a complex structure. Inside the shell there is not hot gas, but an ensemble of rather complexly organized elements - dynamic electric capacitors consisting of electrons and protons moving in closed orbits. The speed of charge movement is close to the speed of light. This makes it possible to generate synchrotron and undulator radiation in the form of a narrow beam.²² The ordered movement of charges in closed orbits opens up the possibility of converting the energy of their motion into electromagnetic radiation of the radio range. Due to the orbital motion of protons, the elements of the core of ball lightning have their own angular momentum. This can explain the reason for the occurrence and cessation of the rotation of ball lightning.²³ The size of the elements of the core of ball lightning can be different. Ball lightning with a size of dynamic capacitors of 1 mm - 1 cm is able to pass through small holes.^4,24

1. Nikitin AI. The danger of ball lightning. Phys Astron Int J. 2023;7(2):91–97.
2. Nikitin AI. Birthplace of ball lightning. Phys Astron Int J. 2024;8(1):38–46.
3. Nikitin AI. Reasons of ball lightning levitation. Phys Astron Int J. 2023;7(4):231–238.
4. Nikitin AI. Traces of the action of ball lightning as material for studying its structure. Phys Astron Int J. 2023;4(1):1–12.
5. Nikitin AI. Ball lightning and unidentified flying objects (UFOs). Phys Astron Int J. 2024;8(1):65–72.
6. Nikitin AI, Bychkov VL, Nikitina TF. High energy ball lightning observations. IEEE Trans. Plasma Sci. 2014;42(12):3906–3911.
7. Tessan de M. Sur la foudre en boule. Compte Rendu. 1859;49:189–191.
8. Anderson O, Baker WR, Bratenahl A. Hydrodynamic capacitor. J Appl Phys. 1959;30:188–196. 
9. Nikitin AI. Electrodynamic model of ball lightning. Khimicheskaya Fizika. 2006;25(3):38–62.
10. Nikitin AI. Possible process of ball lightning training in nature. J Atmos Sol Terr Phys. 2019;190:54–61.
11. Nikitin AI.  My ball lightning. Moscow: Nauka; 2022.
12. Artsimovich LA. Elementary plasma physics. Moscow: Atomizdat; 1969.
13. Frank–Kamenetsky DA. Lectures on plasma physics.  Moscow: Atomizdat; 1968.
14. Landau LD, Lifshits E.M. Field Theory.  Moscow: GIFML; 1960.
15. Artsimovich LA. The controlled thermonuclear reactions. Moscow: GIFML; 1961.
16. Latham R. Vacuum isolation of high voltage installations. Moscow: Atomizdat; 1985.
17. Artsimovich LA, Lukianov SYu.  Movement of charged particles in electric and magnetic fields. Moscow: Nauka; 1978.
18. Moskalyov VA. Betatrons. Moscow: Energoizdat; 1981.
19. Frish SE, Timoreva AV. General physics course. V.1. Moscow: GITTL; 1955.
20. Kittel Ch. Thermal physics. New York: John Willey and Sons, Inc.; 1969.
21. Abramovich GN. Applied gas dynamics. Moscow: Nauka; 1976.
22. Nikitin AI, Nikitin VA, Velichko AM. Features of the mechanism of ball lightning electromagnetic radiation. J Atm Solar–Terr Phys. 2021;222:105711.
23. Nikitin AI. Rotatioinal dynamics of a ball lightning. Phys Astron Int J. 2023;7(3):185–187.
24. Bychkov VL, Nikitin AI, Ivanenko IP, et al. Ball lightning passage through a glass without breaking it.  J Atm Solar–Terr Phys. 2016;150:69–76.