Steady oblique stagnation–point flow of a couple stress fluids on a flat plate is investigated numerically by implementing a well reputed Keller–box method. The plate is lubricated with a slim coating of power–law fluid. Governing partial differential equations of couple stress fluid are converted into ordinary differential equations using similarity transformations. Analysis has been performed by imposing continuity of velocity and shear stress of both the fluids at the interface. Influence of slip and couple stress parameters on the horizontal and shear velocity components, wall shear stress and stagnation point are presented graphically and in the tabular form. The limiting cases for the viscous fluid and no–slip condition have been deduced from the present solutions. The results are compared with already recorded results in the existing research articles and are found in excellent agreement.

Keywords: couple stress fluid, oblique stagnation–point flow, power–law lubricant, continuity of shear stress and velocity, keller–box scheme.

Flow of non–Newtonian fluids has attracted attention of many scientists and researchers because of their fundamental and practical importance in the industry as well as in the daily life. Shear stress of such fluids is non–linearly related with shear rate and it is very difficult to analyze their flow. Examples include food, rubber, gel, polymers, petrol, paper coating, plasma and grease etc. One such fluid is the power–law fluid (Ostwald–de Waele model) which has been used extensively in the industry especially as a lubricant.

Couple stress fluid is another important non–Newtonian fluid first examined by Stokes¹ to describe the polar effects. The couple stress fluid can be described by a new type of tensor called couple stress tensor in addition to the Cauchy stress tensor. In such fluids, polar effects play a significant role which are present due to the couple stresses (moment per unit area) and body couples (moment per unit volume). Because of significant importance of couple stress fluids in the industrial and engineering applications, many researchers have analyzed these flows. Some applications are animal blood, liquid crystals, polymer thickened oil, fluid mechanics and polymeric suspensions. Devakar et al.,² considered Stokes’ problems for the couple stress fluid. In another investigation, Devakar et al.,³ discussed properties of the couple stress fluid flowing between parallel plates. Heat transfer analysis for the flow of a couple stress fluids near a stagnation point has been carried out by Hayat et al.,⁴ Muthuraj et al.,⁵ studied viscous dissipation effects on MHD flow of a couple stress fluid in a vertical channel. Heat transfer analysis by Srinivasacharya et al.,⁶ has been carried out for couple stress flow due to expanding and contracting walls in a porous channel. Flow of couple stress fluid due to free convection through a porous channel was carried out by Hiremath and Patil⁷. Umavathi et al.,⁸ discussed heat transfer analysis for the channel flow of a couple stress fluid sandwiched between two viscous fluids. They showed that couple stress parameter is responsible for enhancing the fluid velocity.

A literature survey reveals that stagnation–point flow can be discussed in two ways either orthogonally or obliquely. Hiemenz⁹ provided an exact solution of stagnation–point flow for the first time. An oblique stagnation–point flow arises when a detached flow of fluid retouches the face of body. Non–orthogonal stagnation–point flow on a wall was examined by Stuart¹⁰ and Tamada¹¹. Dorrepaal¹² found an exact solution for the oblique stagnation–point flow of a viscous fluid. Effects of Weissenberg number on the flow and heat transfer due to stagnation–point was analyzed by Li et al.¹³ Labropulu et al.,¹⁴ discussed heat transfer analysis for the oblique flow impinging on a stretched sheet. Axisymmetric non–orthogonal stagnation–point flow over a circular cylinder has been considered by Weidman and Putkaradze¹⁵. Recently Ghaffari et al.,^16–18 discussed different aspects for the flows towards oblique stagnation point.

Wang¹⁹ discussed the effects of slip parameter on the stagnation point flow of a viscous fluid. Devakar et al.,²⁰ found an exact solution for a couple stress fluid by implementing slip condition at fluid–solid interface. Labropulu et al.,²¹ examined slip flow due to second grade fluid impinging orthogonally or obliquely on a surface. Blyth & Pozrikidis²² studied stagnation point flow by introducing slip condition at the interface of two viscous fluids. Axisymmetric stagnation–point flow near a lubricated stationary disc has been carried out by Santra et al.²³ They used power–law fluid as a lubricant. Sajid et al.²⁴ reconsidered the problem of Santra et al.,²³ by applying generalized slip condition at fluid–lubricant interface introduced by Thompson & Troian.²⁵ Recently Mahmood et el.,²⁶ investigated oblique stagnation–point flow of a second–grade fluid over a plate lubricated by a power–law fluid. Some more recent investigations^27–32 will also be fruitful for the readers.

Our aim in the present communication is to investigate the oblique flow of a couple stress fluids near a stagnation point over a lubricated plate. A power–law fluid has been utilized for the lubrication purpose. The flow problem consists of the set of coupled nonlinear ordinary differential equations along with nonlinear coupled boundary conditions. The Keller–box method^33–36 has been implemented to solve the considered flow problem numerically. Influence of pertinent parameters on the flow characteristics is discussed through graphs and tables. The validity of present study has been checked by comparing results in the limiting case with that exist in the literature.

Consider the steady, two–dimensional, oblique flow of a couple stress fluids towards a stagnation point over a lubricated plate. A power–law fluid (Ostwald–de Waele model) is used as lubricant. The plate is fixed in xz–plane such that it is symmetric with respect to origin. The fluid impinges on the plate with an angle in the domain (Figure 1).

We assume that power–law lubricant spreads on the plate forming a thin coating with the flow rate given as

$Q=\underset{0}{\overset{\delta \left(x\right)}{{\displaystyle \int }}}U\left(x,y\right)dy,$  (1)

where $U\left(x,y\right)$ represents horizontal velocity component of the lubricant and $\delta \left(x\right)$ denotes the variable thickness of the lubrication layer.

The flow problem is governed by the following equations37

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$    (2)

$u\frac{\partial u}{\partial x}+v\frac{\partial u }{\partial y}= -\frac{1}{\rho }\frac{\partial p}{\partial x}+\nu \left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)-{\nu }_1\left(\frac{{\partial }^{4}u}{\partial x^4}+2\frac{{\partial }^{4}u}{\partial x^2\partial y^2}+\frac{{\partial }^{4}u}{\partial y^4}\right),$   (3)

$u\frac{\partial v}{\partial x}+v\frac{\partial v }{\partial y}= -\frac{1}{\rho }\frac{\partial p}{\partial y}+\nu \left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)-{\nu }_1\left(\frac{{\partial }^{4}v}{\partial x^4}+2\frac{{\partial }^{4}v}{\partial x^2\partial y^2}+\frac{{\partial }^{4}v}{\partial y^4}\right),$   (4)

where u and vrepresent, respectively horizontal and vertical velocity components of the couple stress fluid. Parameters $\rho$, $p$ ,$\nu$ and ${\nu }_1$respectively are density, pressure, kinematic viscosity and ratio of couple stress viscosity to the density.

Following Tooke & Blythe³⁸ the free stream velocity components can be written as

$u_e= ax+b\left(y-\overline{\beta }\right), v_e=-a\left(y-\overline{\alpha }\right),$   (5)

where a and b are constants. Furthermore $\overline{\beta }$ is the parameter that supervises the pressure gradient along x–axis which generates the shear flow incident to the orthogonal stagnation–point and the parameter $\overline{\alpha }$ represents the boundary layer displacement produced on the lubricated surface. It is worth to mention that the flow field (5) displays the combined effects of both the horizontal shear flow and the orthogonal stagnation–point flow.

Eliminating the pressure between Eqs. (2) and (3) one obtains

$u\frac{{\partial }^{2}u}{\partial y\partial x}+v\frac{{\partial }^{2}u}{\partial y^2}-u\frac{{\partial }^{2}v}{\partial x^2}-v\frac{{\partial }^{2}v}{\partial x\partial y}-\nu \left(\frac{{\partial }^{3}u}{\partial y\partial x^2}+\frac{{\partial }^{3}u}{\partial y^3}-\frac{{\partial }^{3}v}{\partial x^3}-\frac{{\partial }^{3}v}{\partial x\partial y^2}\right)+$

$u\frac{{\partial }^{2}u}{\partial y\partial x}+v\frac{{\partial }^{2}u}{\partial y^2}-u\frac{{\partial }^{2}v}{\partial x^2}-v\frac{{\partial }^{2}v}{\partial x\partial y}-\nu \left(\frac{{\partial }^{3}u}{\partial y\partial x^2}+\frac{{\partial }^{3}u}{\partial y^3}-\frac{{\partial }^{3}v}{\partial x^3}-\frac{{\partial }^{3}v}{\partial x\partial y^2}\right)+$  (6)

The expression for the skin friction or wall shear stress is given as

${\tau }_w{=\mu \left(\frac{\partial u}{\partial y}\right)|}_{y=0}-{{\mu }_1\left(\frac{{\partial }^{3}u}{\partial y^3}\right)|}_{y=0}$   (7)

where $\mu$ and ${\mu }_1$ are viscosity and couple stress viscosity respectively. The usual no–slip boundary condition at the solid–lubricant interface implies

$U\left(x,0\right)=0 , V\left(x,0\right)= 0.$  (8)

As the power–law coating is very slim, therefore

$V\left(x,y_1\right)=0 , \forall y_1 ϵ \left[0, \delta \left(x\right)\right].$   (9)

We assume that velocity and shear stress of both the fluids are continuous at the interface $y=\delta \left(x\right)$ Thus continuity of shear stress implies

$\mu \frac{\partial u}{\partial y}-{\mu }_1\frac{{\partial }^{3}u}{\partial y^3}={\mu }_L\frac{\partial U}{\partial y}.$  (10)

In which ${\mu }_L$represents the viscosity of the lubricant. Letting $\frac{\partial U}{\partial x}\ll \frac{\partial U}{\partial y}$ the viscosity of lubricant can be written as

${\mu }_L=k{\left(\frac{\partial U}{\partial y}\right)}^{n-1},$    (11)

We further assume that

$U\left(x,y\right)=\frac{\tilde{U}\left(x\right)y}{\delta \left(x\right)}.$   (12)

It is worth to point out that $\tilde{U}\left(x\right)$ is interfacial velocity component of both fluids. The thickness $\delta \left(x\right)$ of the power–law lubricant is given by

$\delta \left(x\right)=\frac{2Q}{\tilde{U}\left(x\right)}.$   (13)

The continuity of horizontal velocity components of both the fluids gives

$\tilde{U}=u$   (14)

Substituting Equations (11)–(14) in Equation (10) we get

$\frac{\partial u}{\partial y}-\frac{{\mu }_1}{\mu }\frac{{\partial }^{3}u}{\partial y^3}=\frac{k}{\mu }{\left(\frac{1}{2Q}\right)}^n{u}^{2n},$   (15)

Similarly implementing the continuity of interfacial velocity components of bulk fluid and lubricant along y–axis we get

$v \left(x,\delta \left(x\right)\right)= V \left(x,\delta \left(x\right)\right),$  (16)

Employing Equation (9) we get

$v \left(x,\delta \left(x\right)\right)= 0.$  (17)

Following Santra et al.,²³ the boundary conditions (15) and (17) can be imposed at the fluid–solid interface. Boundary conditions at free stream have been mentioned in equation (5).

Introducing

$\eta =y\sqrt{\frac{a}{\nu }}, u=ax{f}^{\prime }\left(\eta \right)+a{g}^{\prime }\left(\eta \right), v=- \sqrt{a\nu } f\left(\eta \right),$  (18)

The governing Equations (6), (8), (15), and (17) reduce to

$f^{iv}+f{f}^{‴}+f^{\prime }{f}^{″}-2f\text{'}f\text{'}\text{'}-K{f}^{vi}=0,$   (19)

$g^{iv}+f^{\prime }{g}^{″}+f{g}^{‴}-f^{\prime }{g}^{″}-g^{\prime }{f}^{″}-K{g}^{vi}=0,$   (20)

$f\left(0\right)=0, f\text{'}\text{'}\text{'}\left(0\right)=0, f^{″}\left(0\right)-K{f}^{iv}\left(0\right)=\lambda {\left(f\text{'} \left(0\right)\right)}^{2n},$  (21)

$g\left(0\right)=0, g\text{'}\text{'}\text{'}\left(0\right)=0, g^{\text{'}\text{'}}\left(0\right)-K{g}^{iv}\left(0\right)=2n\lambda g^{\prime }\left(0\right){\left(f^{\prime }\left(0\right)\right)}^{2n-1},$  (22)

$g^{″}\left(\infty \right)=\gamma ,$(23)

Where $K={\nu }_1{a}^2/{\nu }^2$ is called the couple stress parameter and $\gamma =b/a$ denotes the free stream shear. The parameter $\lambda$ in Equations (21) and (22) is given as

$\lambda =\frac{k\sqrt{\nu }}{\mu } \frac{a^{2n }{x}^{2n-1}}{a^{3/2} {\left(2Q\right)}^n}$$f^{‴}-{f^{\prime }}^2+f{f}^{″}+1-K{f}^v=0,$ (24)

Integrating Equations (19) and (20) and using free stream conditions, we get

$f^{‴}-{f^{\prime }}^2+f{f}^{″}+1-K{f}^v=0,$   (25)

$g^{‴}+f{g}^{″}-f\text{'}g\text{'}-K{g}^v=\gamma \left(\beta -\alpha \right),$   (26)

Where $\beta$ is a free parameter and $\alpha ={\eta }_{\infty }-f\left(\infty \right)$ . In order to eliminate $\gamma$ from Equation (26)we let $g^{\prime }\left(\eta \right)=\gamma h\left(\eta \right)$ to obtain

$h^{″}+f{h}^{\prime }-f^{\prime }h-K{h}^{iv}=\beta -\alpha .$    (27)

The boundary conditions in new variables become

$h^{″}\left(0\right)=0, h^{\text{'}}\left(0\right)-K{h}^{‴}\left(0\right)=2n\lambda h\left(0\right){\left(f\text{'}\left(0\right)\right)}^{2n-1}, h^{\text{'}}\left(\infty \right)=1.$    (28)

Equation (24) suggests that to obtain similar solution, one should have $n=\text{½}$ . The parameter $\lambda$ given in Equation (24) measures slip produced on the surface and can be written as

$\lambda =\frac{\sqrt{\frac{\nu }{a}}}{\frac{\mu }{k}\sqrt{2Q}}=\frac{L_{visc}}{L_{lub}} .$   (29)

As clear from Equation (29),$\lambda$ is a representation of ratio of viscous length scale$L_{visc}$ to the lubrication length scales $L_{lub}$ . For a highly viscous bulk fluid (i.e. when $L_{visc}$ is large) and a very thin lubricant (i.e. when $L_{lub}$ is small), the parameter$\lambda$ is increased. As the parameter $\lambda$ approaches to infinity, the traditional no–slip conditions $f^{\prime }\left(0\right)=0$ , and$h\left(0\right)=0$can be recovered from Equations (21) and (28). On the other hand when the bulk fluid is less viscous and $L_{lub}$ attains a massive value,$\lambda \to 0$ and consequently the full slip boundary conditions $f^{\prime }\left(0\right)=0,f^{iv}\left(0\right)=0$, $h^{\prime }\left(0\right)=0$ and $h^{‴}\left(0\right)=0$are achieved.Therefore $\lambda$ interprets the inverse measure of slip called slip parameter.

Employing (18), the dimensionless wall shear stress is given by

${\tau }_w=x\left(f^{″}\left(0\right)-K{f}^{iv}\left(0\right)\right)+\left(g^{″}\left(0\right)-K{g}^{iv}\left(0\right)\right)$

$=x\left(f^{″}\left(0\right)-K{f}^{iv}\left(0\right)\right)+\gamma \left(h\text{'}\left(0\right)-K{h}^{‴}\left(0\right)\right)$  (30)

To find the stagnation–point$x_s$ on the surface, we set ${\tau }_w=0$  Therefore

$x_s=-\frac{g^{″}\left(0\right)-K{g}^{iv}\left(0\right)}{f^{″}\left(0\right)-K{f}^{iv}\left(0\right)}=-\gamma \frac{h^{\prime }\left(0\right)-K{h}^{‴}\left(0\right)}{f^{″}\left(0\right)-K{f}^{iv}\left(0\right)}.$   (31)

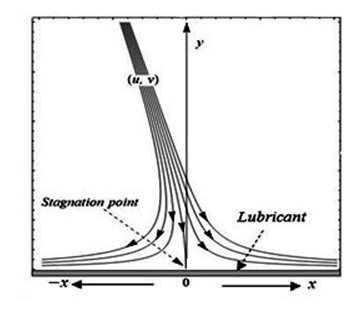
Figure 1 Reported bird strikes and parts mostly hit(* FAA wildlife strike data base).

Equations (21), (25), (27) and (28) are solved using Keller–box method^33–36 which is based on an implicit finite difference approach. This numerical scheme is very effective to solve non–linear and coupled boundary value problems directly without converting them into initial value problems. As a first step, a system of first order ordinary differential equations is obtained in the following way:

$f^{\prime }=u, u^{\prime }=v, v^{\prime }=w, w^{\prime }=p, h\text{'}=U, U\text{'}=V, V\text{'}=W,$  (32)

Therefore, Equations (25) and (27) imply

$w-u^2+fv+1-Kp\text{'}=0,$

$V+fU-uh-K{W}^{\prime }=\beta -\alpha$  (33)

The transformed boundary conditions n=0.5 for  imply

$f\left(0\right)=0, w\left(0\right)=0, v\left(0\right)-Kp\left(0\right)=\lambda u\left(0\right), u\left(\infty \right)=1,$  (34)

$V\left(0\right)=0, U\left(0\right)-KW\left(0\right)=\lambda h\left(0\right), U\left(\infty \right)=1,$  (35)

The obtained first–order system is approximated with central–difference for derivatives and averages for the dependent variables. The reduced algebraic system is given by

$\frac{f_j-f_{j-1}}{k_j}=u_{j-\frac{1}{2}}$,$\frac{u_j-u_{j-1}}{k_j}=v_{j-\frac{1}{2}}$ ,$\frac{v_j-v_{j-1}}{k_j}=w_{j-\frac{1}{2}}$, $\frac{w_j-w_{j-1}}{k_j}=p_{j-\frac{1}{2}}$ ,    (36)

$\frac{h_j-h_{j-1}}{k_j}=U_{j-\frac{1}{2}}$,$\frac{U_j-U_{j-1}}{k_j}=V_{j-\frac{1}{2}}$ , $\frac{V_j-V_{j-1}}{k_j}=W_{j-\frac{1}{2}}$   (37)

$w_{j-\frac{1}{2}}-u^2{}_{j-\frac{1}{2}}+f_{j-\frac{1}{2}} v_{j-\frac{1}{2}}+1-K\left(\frac{p_j-p_{j-1}}{k_j}\right)=0,$(38)

$V_{j-\frac{1}{2}}+f_{j-\frac{1}{2}} U_{j-\frac{1}{2}}-u_{j-\frac{1}{2}} h_{j-\frac{1}{2}}+1-K\left(\frac{W_j-W_{j-1}}{k_j}\right)=0,$  (39)

where$f_{j-\frac{1}{2}} =\frac{f_j+f_{j-1}}{2}$ etc. Equations (38) and (39) are nonlinear algebraic equations and therefore, have to be linearized before the factorization scheme can be used. We write the Newton iterates in the following way:

For the $\left(j+1\right)th$ iterates:

$f_{j+1}=f_j+\delta f_j,etc.,$   (40)

for all dependent variables. By substituting these expressions in Equations (36)–(39) and dropping the quadratic and higher–order terms in $\delta f_j$ , a linear tridiagonal system of equations will be obtained as follows:

$\delta f_j-\delta f_{j-1}-k_j\left(\frac{u_j+u_{j-1}}{2}\right)={\left(r_1\right)}_{j-\frac{1}{2}} , \delta u_j-\delta u_{j-1}-k_j\left(\frac{v_j+v_{j-1}}{2}\right)={\left(r_2\right)}_{j-\frac{1}{2}} ,$ (41)

$\delta v_j-\delta v_{j-1}-k_j\left(\frac{w_j+w_{j-1}}{2}\right)={\left(r_3\right)}_{j-\frac{1}{2}} ,\delta w_j-\delta w_{j-1}-k_j\left(\frac{p_j+p_{j-1}}{2}\right)={\left(r_4\right)}_{j-\frac{1}{2}} ,$   (42)

$\left({\psi }_1\right)\delta f_j+\left({\psi }_2\right)\delta f_{j-1}+\left({\psi }_3\right)\delta u_j+\left({\psi }_4\right)\delta u_{j-1}+ \left({\psi }_5\right)\delta v_j+\left({\psi }_6\right)\delta v_{j-1}+$

$\left({\psi }_7\right)\delta w_j+\left({\psi }_8\right)\delta w_{j-1}+\left({\psi }_9\right)\delta p_j+\left({\psi }_{10}\right)\delta p_{j-1}={\left(r_5\right)}_{j-\frac{1}{2}} ,$   (43)

$\delta h_j-\delta h_{j-1}-k_j\left(\frac{U_j+U_{j-1}}{2}\right)={\left(r_6\right)}_{j-\frac{1}{2}} , \delta U_j-\delta U_{j-1}-k_j\left(\frac{V_j+V_{j-1}}{2}\right)={\left(r_7\right)}_{j-\frac{1}{2}} ,$   (44)

$\delta V_j-\delta V_{j-1}-k_j\left(\frac{W_j+W_{j-1}}{2}\right)={\left(r_8\right)}_{j-\frac{1}{2}} ,$   (45)

$\left({\mu }_1\right)\delta f_j+\left({\mu }_2\right)\delta f_{j-1}+\left({\mu }_3\right)\delta u_j+\left({\mu }_4\right)\delta u_{j-1}+\left({\mu }_5\right)\delta h_j+\left({\mu }_6\right)\delta h_{j-1}+$ $\left({\mu }_7\right)\delta U_j+\left({\mu }_8\right)\delta U_{j-1}+\left({\mu }_9\right)\delta V_j+\left({\mu }_{10}\right)\delta V_{j-1}={\left(r_9\right)}_{j-\frac{1}{2}} ,$    (46)

subject to boundary conditions

$\delta f_0=0, \delta w_0=0,\lambda \delta u_0-\delta v_0+K\delta p_0=v_0-K{p}_0-\lambda u_0,$   (47)

$\delta V_0=0,\lambda \delta h_0-\delta U_0+K\delta W_0=U_0-K{W}_0-\lambda h_0,$  (48)

where ${\left({\psi }_1\right)}_j={\left({\psi }_2\right)}_j=\frac{k_j}{4}\left(v_j+v_{j-1}\right)$ etc. The resulting linearized system of algebraic equations is solved by the block–elimination method. In matrix–vector form, the above system can be written as

$A\delta =r,$   (49)

in which

$A=\left[\begin{array}{ccccccc}\left[A_1\right]& \left[C_1\right]& & & & & \\ \left[B_1\right]& \left[A_2\right]& \left[C_2\right]& & & & \\ & \ddots & \ddots & \ddots & & & \\ & & \ddots & \ddots & \ddots & & \\ & & & \ddots & \ddots & \ddots & \\ & & & & \left[B_{J-1}\right]& \left[A_{J-1}\right]& \left[C_{J-1}\right]\\ & & & & & \left[B_J\right]& \left[A_J\right]\end{array}\right],\delta =\left[\begin{array}{c}\left[{\delta }_1\right]\\ \left[{\delta }_2\right]\\ \ddots \\ \left[{\delta }_{J-1}\right]\\ \left[{\delta }_J\right]\end{array}\right],r=\left[\begin{array}{c}\left[r_1\right]\\ \left[r_2\right]\\ \ddots \\ \left[r_{J-1}\right]\\ \left[r_J\right]\end{array}\right],$   (50)

where the elements inA are of $9\times 9$matrices and that of $\delta$ and $r$are respectively of order $9\times 1$ . Now, we let

$A=LU,$   (51)

where L is a lower and U is an upper triangular matrix.

Equation (51) can be substituted into Equation (49) to get

$LU\delta =r.$   (52)

Defining

$U\delta =W,$ (53)

Equation (52) becomes

$LW=r,$ (54)

where the elements of $W$are $9\times 1$ column matrices. The elements of$W$ can be solved from Equation (54). Once the elements of$W$ are found, Equation (53) then gives the solution$\delta$. When the elements of $\delta$ are found, Equation (49) can be used to find the next iteration.

The values of $f\text{'}$ and $h\text{'}$ are displayed graphically for different values of $\lambda$,$K$ and$\beta$ and $\beta$ are presented in Figures 2–6. The influences of pertinent parameters on the streamlines have been shown in Figures 7–8 while the impact of these parameters on$f^{″}\left(0\right)$,$\alpha$,$h^{\text{'}}\left(0\right)$ and stagnation points are displayed in Tables 1–5. The comparison of numerical values of $f^{″}\left(0\right)$,$\alpha$ and $h^{\text{'}}\left(0\right)$ in the special cases with that of existing in the literature are presented in Tables 6–7.

Figure 2 displays the variation in horizontal velocity component under the influence of slip parameter $\lambda$. Dashed lines show the results for viscous and solid lines for the couple stress fluid. We observe that $f\text{'}$ decreases by decreasing $\lambda$ . Moreover, couple stress parameter enhances the effects of slip parameter. Analysis showing the impact of couple stress parameter k on $f\text{'}$ for fixed $\lambda$ is presented in Figure 3. It is clear from this figure that $f\text{'}$ is an increasing function of k. We observe some alteration inside the boundary layer. However, the curve becomes smooth at the free stream. Effects of slip parameter $\lambda$ on $h\text{'}$ for two values of $\beta$ when $K= 0.5$ have been provided in Figure 4. According to this figure $h\text{'}$ decreases for positive values of and increases for negative values of $\beta$. Figure 5 is displayed to analyze the behavior of $h\text{'}$under the influence of $\beta$both for the no–slip and partial slip cases. It is noted that an increment in the value of $\beta$ results in the decrease of $h\text{'}$ . This decrease is more significant on the rough surface (when $\lambda \to \infty$ ). Influence of parameter $\beta$ on $h\text{'}$ for two values of k when $\lambda =2$ is presented in Figure 6. The analysis shows that $h\text{'}$ decreases by increasing $\beta$ .This decrease is diminished by enlarging couple stress parameter k.

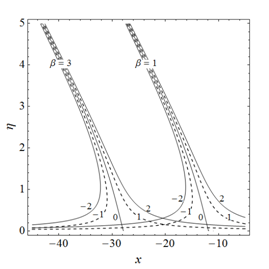
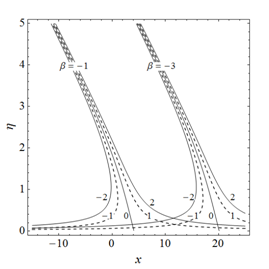
The streamlines explored in Figure 7 show the influence of $\beta$on the stagnation point in the presence of slip when $\gamma =8 \text{and} K=0.5$ . It has been observed that the stagnation point moves towards left by increasing $\beta$. Streamlines showing the impact of slip and couple stress parameters are expressed in Figure 8. It is evident that stagnation point shifts towards right by increasing $\lambda$ as well as k when $\beta =0$ .

Influence of parameters $\lambda$and k on the skin friction coefficient $\lambda$and boundary layer displacement $\alpha$has been provided through Table 1. It is observed through Table 1 that $f^{″}\left(0\right)$increases by increasing $\lambda$and decreases by increasing k. Likewise, $\alpha$is increased by enhancing $\lambda$ and k independently.Impact of $\lambda$ on $h^{\text{'}}\left(0\right)$ is shown in Table 2. It has been observed that $h^{\text{'}}\left(0\right)$gains the magnitude by enhancing $\lambda$for $\beta \le 0$ and loses for $\beta >0$. Data showing $h^{\text{'}}\left(0\right)$for various values of k is represented through Table 3. It is observed that $h^{\text{'}}\left(0\right)$ gains the magnitude as k is accelerated for $\beta \ge 0$and loses its values for $\beta <0$ . The movement of the stagnation point under the influence of increasing $\lambda$,k and $\beta$ is demonstrated through Tables 4–5. We observe that stagnation point moves towards right on the x–axis by raising both $\lambda$and K while it shifts leftwards by augmenting $\beta$. The tabular results shown in Tables 4–5 do confirm the investigations made through Figures 7–8.

The numerical data regarding $f^{″}\left(0\right)$,$\alpha$ and $h\text{'}\left(0\right)$in the limiting case (when $\lambda \to \infty$) acknowledges the values already recorded in the research articles.^13,14 This evidence certifies the correctness of our investigation.

Figure 2 Effects of slip parameter$\lambda$ on $f\text{'}\left(\eta \right)$ for viscous and couple stress fluids.

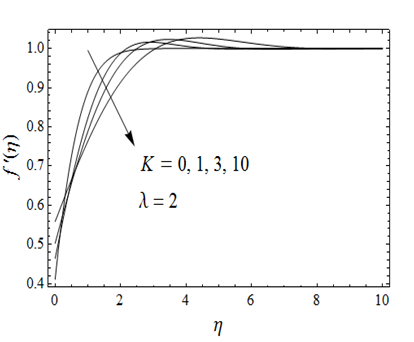
Figure 3 Impact of couple stress parameter k on $f\text{'}\left(\eta \right)$ when $\lambda =2$ .

Figure 4 Influence of slip parameter $\lambda$ on $h\text{'}\left(\eta \right)$ when $K= 0.5$ for two different values of$\beta$ .

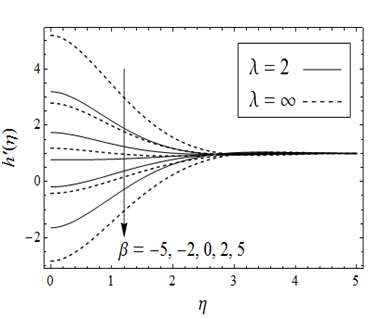
Figure 5 Influence of parameter$\beta$ on $h\text{'}\left(\eta \right)$ when $K= 0.5$ for two different values of $\lambda$.

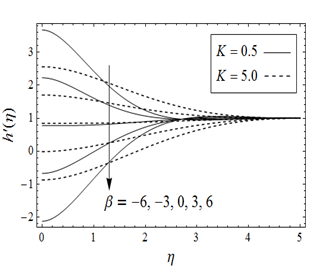
Figure 6 Influence of parameter $\beta$ on $h\text{'}\left(\eta \right)$ when $\lambda = 2$  for different values of k.

(A)$\gamma =8, K=0.5, \lambda =0.5$

(B)$\gamma =8, K=0.5, \lambda =0.5$

Figure 7 Streamlines showing the effects of parameter $\beta$

.

In this paper, oblique flow of a couple stress fluids near stagnation point over a lubricated plate is investigated. A power–law fluid has been used as a lubricant. To obtain similar solution of the flow problem, we have fixed $n=1/2$. The Keller–box method is employed to solve the flow problem numerically. Our interest is to figure out the effects of free parameter$\beta$and couple stress parameter k on the flow characteristics on the lubricated surface. Obtained results in the special case are compared.^13,14 It has been concluded that:

1. Slip produced on the surface increases the velocity of the bulk fluid and abolishes the effects of free stream velocity for large values.
2. The stagnation point is shifted towards right and left along $x$–axis under the influence of physical parameters in the presence of lubrication.
3. The skin friction coefficient $f^{″}\left(0\right)$increases by increasing $\lambda$and decreases by increasing k. However boundary layer displacement $\alpha$is increased by enhancing $\lambda$ and/or k .
4. It has been observed that $h^{\text{'}}\left(0\right)$ gains the magnitude by enhancing $\lambda$ for $\beta \le 0$ and loses for $\beta >0$.Data showing$h^{\text{'}}\left(0\right)$ for various values of k is represented through Table 3. It is observed that $h^{\text{'}}\left(0\right)$ gains the magnitude as k is accelerated for$\beta \ge 0$ and loses its values for $\beta <0$ .

Author declares there is no conflict of interest.

1. Stokes VK. Couple stresses in fluids. Physics of Fluids. 1966;9(9):1709–1715.
2. Devakar M, Iyengar TKV. Run up flow of a couple stress fluid between parallel plates. Non–linear Analysis: Modelling and Control. 2010;15(1):29–37.
3. Devakar M, Iyengar TKV. Stokes’ problems for an incompressible couple stress fluid. Non–linear Analysis: Modelling and Control. 2008;1(2):181–190.
4. Hayat T, Mustafa M, Iqbal Z, et al. Stagnation point flow of couple stress fluid with melting heat transfer. Applied Mathematics and Mechanics. 2013;34(2):167–176.
5. Muthuraj R, Srinivas S, Immaculate DL. Heat and mass transfer effects on MHD fully developed flow of a couple stress fluid in a vertical channel with viscous dissipation and oscillating wall temperature. International Journal of Applied Mathematics and Mechanics. 2013;9:95–117.
6. Srinivasacharya D, Srinivasacharyulu N, Odelu O. Flow and heat transfer of couple stress fluid in a porous channel with expanding and contracting walls. International Communications in Heat and Mass Transfer. 2009;36(2):180–185.
7. Hiremath PS, Patil PM. Free convection effects on the oscillating flow of a couple stress fluid through a porous medium. Acta Mechanica. 1993;98:143–158.
8. Umavathi JC, Chamka AJ, Manjula MH, et al. Flow and heat transfer for a couple stress fluid sandwiched between viscous fluid layers. Canadian Journal of Physics. 2005;83(7):705–720.
9. Hiemenz K. Die Grenzschicht an einem in den gleichformingen Flussigkeitsstrom eingetauchten graden Kreiszylinder. Dinglers Polytech Journal. 1911;326:321–324.
10. Stuart JT. The viscous flow near a stagnation–point when the external flow has uniform vorticity. Journal of the Aerospace Sciences. 1959;26;124–125.
11. Tamada KJ. Two–dimensional stagnation–point flow impinging obliquely on a plane wall. Journal of the Physical Society of Japan. 1979;46:310–311.
12. Dorrepaal JM. An exact solution of the Navier–Stokes equation which describes non–orthogonal stagnation–point flow in two dimensions. Journal of Fluid Mechanics. 1986;163:141–147.
13.  Li D, Labropulu F, Pop I. Oblique stagnation–point flow of a viscoelastic fluid with heat transfer. International Journal of Non–Linear Mechanics. 2009;44:1024–1030.
14. Labropulu F, Ghaffar A. Oblique Newtonian fluid flow with heat transfer towards a stretching sheet. Computational Problems in Engineering. 2014;307:93–103.
15. Weidman PD, Putkaradze V. Axisymmetric stagnation flow obliquely impinging on a circular cylinder. European Journal of Mechanics. 2003;22(2):123–131.
16. Ghaffari T, Javed, Labropulu F. Oblique stagnation point flow of a non–Newtonian nanofluid over stretching surface with radiation: A numerical study. Thermal Science. 2015;21(5):2139–2153.
17. Javed T, Ghaffari A, Ahmad H. Numerical study of unsteady MHD oblique stagnation point flow with heat transfer over an oscillating flat plate. Canadian Journal of Physics. 2015;93(10):1138–1143.
18. Ghaffari A, Javed T, Majeed A. Influence of radiation on non–Newtonian fluid in the region of oblique stagnation point flow in a porous medium: A numerical study. Transport in Porous Media. 2016;113(1):245–266.
19. Wang CY. Stagnation flows with slip: Exact solution of the Navier–Stokes equations. Zeitschrift für angewandte Mathematik und Physik ZAMP. 2003;54(1):184–189.
20. Devakar M, Sreenivasu D, Shankar B. Analytical solution of couple stress fluid flows with slip boundary condition. Alexandria Engineering Journal. 2014;53(3):723–730.
21. Labropulu F, Li D. Stagnation–point flow of a second–grade fluid with slip. International Journal of Non–Linear Mechanics. 2008;43(9):941–947.
22. Blyth MG, Pozrikidis C. Stagnation–point flow against a liquid film on a plane wall. Acta Mechanica. 2005;180(4):203–219.
23. Santra B, Dandapat BS, Andersson HI. Axisymmetric stagnation–point flow over a lubricated surface. Acta Mechanica. 2007;194(4):1–10.
24. Sajid M, Mahmood K, Abbas Z. Axisymmetric stagnation–point flow with a general slip boundary condition over a lubricated surface. Chinese Physics Letters. 2012;29(2):024702.
25. Thompson PA, Troian SM. A general boundary condition for liquid flow at solid surfaces. Nature. 1997;389:360–362.
26. Mahmood K, Sajid M, Ali N. Non–orthogonal Stagnation–point Flow of a Second–grade Fluid Past a Lubricated Surface. ZNA. 2016;71(3):273–280.
27. Mehmood R, Rana S,  Nadeem S. Transverse thermopherotic MHD Oldroyd–B fluid with Newtonian heating. Results in Physics. 2018;8:686–693.
28. Tabassum R, Mehmood R, Akbar NS. Magnetite micropolar nanofluid non–aligned MHD flow with mixed convection. The European Physical Journal Plus. 2017;132:275.
29. Tabassum R, Mehmood S, Nadeem S. Impact of viscosity variation and micro rotation on oblique transport of Cu–water fluid. Journal of Colloid and Interface Science. 2017;501:304–310.
30. Mehmood R, Nadeem S, Saleem S. Flow and heat transfer analysis of Jeffery nano fluid impinging obliquely over a stretched plate. Journal of the Taiwan Institute of Chemical Engineers. 2017;74:49–58.
31. Rana S, Mehmood R, Narayana PVS, et al. Free convective nonaligned non–Newtonian flow with non–linear thermal radiation. Communications in Theoretical Physics. 2016;66(6):687–693.
32. Rana S, Mehmood R, Akbar NS. Mixed convective oblique flow of a Casson fluid with partial slip, internal heating and homogeneous–heterogeneous reactions. Journal of Molecular Liquids. 2016;222:1010–1019.
33. Na TY. Computational Methods in Engineering Boundary Value Problem. USA: Academic Press; 1979.
34. Cebeci T, Bradshaw P. Physical and Computational Aspects of Convective Heat Transfer. USA: Springer; 1984.
35. Keller HB, Cebeci T. Accurate Numerical Methods for Boundary Layer Flows II: Two Dimentional Turbulent Flows. AIAA Journal. 1972;10(9):1193–1199.
36. Keller HB. A new difference scheme for parabolic problems, in Numerical Solution of Partial–Differential Equations. In: Bramble J, editor. USA: Academic Press; 1970.
37. Ramesh K, Devakar M. Effects of Heat and Mass Transfer on the Peristaltic Transport of MHD Couple Stress Fluid through Porous Medium in a Vertical Asymmetric Channel. Journal of Fluids; 2015:1–20.
38. Tooke RM, Blyth MG. A note on oblique stagnation–point flow. Physics of Fluids. (2008);20(3).