This paper presents the Ulianov Orbital Model (UOM), a simplified approach to two-body orbital mechanics. The UOM provides equations to calculate the standard ellipse parameters (a and b) and orbital trajectories and velocities from three UOM basic parameters (Ue, R0, and V0). It introduces a new kind of elliptical trigonometric functions, which simplify plotting orbital trajectories and their velocities over time and in elliptical angular steps. The Ulianov Elliptic Transform (UET), generates an impressive effect of rotating and scaling an ellipse, transferring its center from one of the foci to the geometric center of the ellipse. The UET offers a new and easy way to create and manipulate ellipses using both numerical and analytical methods.

Keywords: Ulianov Orbital Model, Elliptical trigonometric functions, Ulianov Elliptic Transform, Orbital trajectories

In celestial mechanics, the problem of two bodies interacting gravitationally is traditionally described using Keplerian orbits or the Newtonian approach. A Kepler orbit, named after Johannes Kepler,¹ describes the motion of a body with small mass ( $M_a$ ) relative to another body with a large mass ( $M_b$ ). Due to the difference in masses, the movement of the body $M_b$ in space is not significantly affected by the interaction with the body $M_a$ . Therefore, $M_b$ can often be considered stationary or defined as the origin of the coordinate system used to define the movement of . This assumption defines the Kepler orbit problems and is valid for many cases, such as the movement of planets around the sun, communication satellites around the Earth, or small moons (such as the moons of Mars). However, it is not valid for the orbit of Earth’s moon because the difference in masses is smaller, causing the moon’s mass to make the Earth oscillate in its trajectory. When the mass $M_a$ is much smaller than $M_b$ , the orbit becomes an ellipse, parabola, or hyperbola. The Kepler Orbit Model (KOM)² requires six orbital elements to fully describe the motion of the body $M_a$ :

• Eccentricity ( $e$ ): The shape of the ellipse.
• Semi-major axis ( $a$ ): Half the distance between the apoapsis and periapsis.
• Inclination ( $i$ ): The tilt of the orbital plane.
• Longitude of the ascending node ( $\Omega$ ): The horizontal orientation of the ascending node.
• Argument of periapsis ( $\omega$ ): The orientation of the ellipse in the orbital plane.
• True anomaly (velocity $\nu$ ,at angle $\theta$ ,) at epoch ( $t_0$ ): The position of the orbiting body along the ellipse at a specific time.

Note: Although these parameters are defined as six orbital elements, there are eight values listed, so we can also consider that the KOM has eight individual numeric parameters.

The Newtonian model,³ which solves the problem using numerical methods, requires a similar number of parameters. A complete simulation can be defined by the masses of the bodies ( $M_b,M_a$ ) and their initial positions $\left(x,y,z\right)$ and velocities $\left(v_x,v_y,v_z\right)$ and a time reference $t_0$ , totaling nine values. If we consider a reference system that defines the $\left(x,y\right)$ plane over the elliptical plane, the numerical methods can use only seven parameters: masses $M_b$ , $M_a$ , and initial positions $\left(x,y\right)$ and velocities $\left(v_x,v_y\right)$ and a time reference $t_0$ .

The Ulianov Orbital Model introduces a new approach that reduces the complexity to only five parameters (seven numerical values) because the ellipse shape is represented by only one parameter, named the Ulianov Ellipse parameter ( $U_e$ ), while maintaining accuracy in the ellipse representation and also defining parabolas and hyperbolas. Additionally, it offers a methodology that facilitates the orbit position and velocity calculation by applying two Ulianov Elliptic trigonometric functions (cosuell( $\alpha ,U_e$ ) and sinuell( $\alpha ,U_e$ )) to calculate the UOM elliptical orbit positions and velocities. The UOM also provides routines for determining these parameters from data observed in the body trajectory.

The Ulianov Orbital Model (UOM) characterizes an orbit using the following five parameters:

1. Inclination ( i ): The vertical tilt of the ellipse with respect to the reference plane.
2. Longitude of the ascending node ( Ω ): The horizontal orientation of the ascending node.
3. Argument of periapsis (ellipse angle$E_{ang}$ ): The orientation of the ellipse in the orbital plane.
4. Initial condition, given by the minimum orbital distance ( $R_0$ ) (the minimum distance between the orbital body and the central body), the maximum velocity ( $V_0$ ) (the velocity at $R_0$ distance, which is the maximum velocity in the orbit) at epoch ( $t_0$ ) (UTC time for an angle α= 0, occurring at the point $\left(x_e,y_e\right)=\left(R_0,0\right)$ and velocity $\left(v_x,v_y\right)=\left(0,V_0\right)$ ).
5. Ulianov elliptical parameter ( $U_e$ ): Defines the shape and size of the orbit.

Although these parameters are defined as five orbital elements, there are seven values defined in this list, so we can also consider that the UOM has seven individual numeric parameters.

Note that the UOM provides a reduction of one parameter compared to the KOM because the parameters eccentricity ( $e$ ) and semi-major axis ( $a$ ) are replaced by only one parameter, the Ulianov Ellipse parameter ( $U_e$ ), with some advantages:

• The application of elliptic trigonometric functions (cosuell( $\alpha ,U_e$ ) and sinuell( $\alpha ,U_e$ )) to determine the orbit values and velocities as a function of any given time or ellipse angle.
• The easy obtaining of the elliptic orbit range (standard ellipse parameters a and b or eccentricity ( e )) and period from initial values $R_0$ and $V_0$ or generic positions ( $e_x,e_y$ ) and velocities ( $v_x,v_y$ ) defined in the ellipse orbit.

Another important aspect is that the Keplerian orbital model stores an angular position in the orbit and a velocity for a specific time, which can be, for example, close to a present time of interest. This scheme is used because, normally, to move this point within the orbit, numerical simulations based on the Newtonian method are necessary, which must be calculated with a very small time interval $dt$ , making it faster to calculate the orbit from the defined time to a new time for nearby times. In the case of the UOM, the model parameter stores the time, position, and velocity for the angle α equal to zero because the model can very quickly calculate the position and velocity for any desired time or angle.

The Ulianov Elliptical Parameter $U_e$ value is calculated by the equation:

$U_e=\frac{V_0^2{R}_0}{G{M}_b}$                         (1)

where $G$ is the gravitational constant and $M_b$ is the mass of the primary body.

The Ulianov elliptical parameter eliminates the need to explicitly include $M_b$ and $G$ in the calculations, and also defines the velocity over the orbit and the complete elliptical orbit path, simplifying the model. However, to understand how the parameter $U_e$ works, we need to first observe some basic definitions.

The general solution for the elliptical orbit is given by:

$\begin{array}{rr}\hfill \frac{x^2}{a^2}& \hfill +\frac{y^2}{b^2}=1\\ \hfill x_e\left(\alpha \right)& \hfill =a\text{cos}\left(\alpha \right)\\ \hfill y_e\left(\alpha \right)& \hfill =b\text{sin}\left(\alpha \right)\end{array}$

where a and b are the semi-major and semi-minor axes of the ellipse, respectively. Note that the α angle is defined in the ellipse center, instead of being centered on the focus where the orbited body is located, which normally defines the origin of the system in both Cartesian and polar coordinates. In this way, these ellipse equations, despite being very simple, do not perform well in the case of a coordinate system centered on the orbited body. Additionally, the values a and b need to be calculated from some observed positions and velocities of the body in orbit. For certain initial velocities, a and b become very large and exhibit chaotic behavior, because very small changes in the initial orbital velocity ( $V_0$ ) can generate large variations in the a and b values. This chaotic behavior difficult to calculate a and b values using analytics solutions of differential equations, requiring numerical simulation to obtain these parameters. These simulations are normally based on the calculation of forces and acceleration in a small time interval (in the order of fractions of a second) to be precise. For larger orbits, with periods of many years or even many centuries, a large number of processing steps are needed to determine complete orbit positions and velocities. To use an angle α centered in the ellipse focus, we can consider an ellipse equation defined as:

$\begin{array}{rr}\hfill x_e\left(\alpha \right)& \hfill =R_0{K}_x\text{cos}\left(\alpha \right)-R_0\left(K_x-1\right)\\ \hfill y_e\left(\alpha \right)& \hfill =R_0{K}_y\text{sin}\left(\alpha \right)\end{array}$

where the ellipse’s foci are in the x axis direction and for $a>b$ ,$R_0$ is the minimum orbital radius and $K_x$ , $K_y$ are gain factors that can be calculated by:

$\begin{array}{rr}\hfill R_0& \hfill =a-\sqrt{a^2-b^2}\\ \hfill K_x& \hfill =\frac{a}{R_0}\\ \hfill K_y& \hfill =\frac{b}{R_0}\end{array}$

Note: These definitions consider that the angle α  starts at 0° and rotates counterclockwise. At $\alpha =0$ , $x_e=R_0$ , $y_e=0$ , $v_x=0$ , and $v_y=V_0$ .

The velocity $V\left(d_e\right)$ of body $M_a$ along its trajectory is defined by the conservation of energy equation:

$\begin{array}{rr}\hfill \frac{1}{2}{M}_{a}V{\left(d_e\right)}^2& \hfill =\frac{1}{2}{M}_a{V}_0^2-\frac{G{M}_b{M}_a}{R_0}+\frac{G{M}_b{M}_a}{d_e}\\ \hfill V{\left(d_e\right)}^2& \hfill =V_0^2-2\frac{G{M}_b}{R_0}+2\frac{G{M}_b}{d_e}\end{array}$               (2)

Considering the Ulianov Elliptical Factor $U_e$ defined in Equation (1), Equation (2) becomes the Ulianov orbital velocity equation:

$\begin{array}{rr}\hfill d_e& \hfill =\sqrt{x_e^2+y_e^2}\\ \hfill V{\left(d_e\right)}^2& \hfill =V_0^2\left(1-\frac{2}{U_e}\left(\frac{R_0}{d_e}-1\right)\right)\end{array}$                      (3)

Note that at this point we need two additional parameters to represent the elliptical orbit: The values of gains $K_x$ , and $K_y$ that not are included in the UOM parameter list presented at beginning of this section. Otherwise, as will be demonstrated in the next section, the $U_e$ parameter allows the calculation of the $K_x$ and $K_y$ values, reducing this model to only five parameters (seven values in total), an new result that was obtained by applying the Ulianov Elliptical Transform.

Analyzing Equation (3), we can observe that the nature of the orbit depends on the value of $U_e$ . Considering that in this equation the $d_e$ value is equal to $R_0$ , the $V\left(d_e\right)$ value is equal to $V_0$ . Considering that the $d_e$ value tends to infinity, Equation (3) can be defined as:

$\begin{array}{rr}\hfill V\left(\infty \right)& \hfill =V_0\sqrt{\left(1-\frac{2}{U_e}\right)}\end{array}$                        (4)

In Equation (4), for $0<U_e<2$ , we have the root of a negative number, which indicates that in this range of values the value of $d_e$ will be limited and will never reach infinity. Therefore, this range of $U_e$ values defines a closed curve, which is the ellipse.

For $U_e=2$ , the $V\left(\infty \right)$ value is equal to zero, marking the limit of the ellipse range, with the $K_x$ parameter tending to infinity, which also defines a parabola.

For $U_e>2$ , the $V\left(\infty \right)$ value is greater than zero, and the $U_e$ value defines a hyperbola.

Based on this analysis, the $U_e$ parameter can be used to define a total of six types of orbits:

• $U_e=0$ : The body has a velocity $V_0$ pointing along the radial line, or $V_0=0$ . This indicates that the $M_a$ body is in a direct collision trajectory, defined by a straight line to the body $M_b$ .
• $U_e=1$ : The trajectory is circular, representing that $V_0$ is equal to the orbital velocity.
• $0<U_e<1$ : The trajectory is an ellipse, but the $R_0$ value is the maximum orbital radius and $V_0$ is the minimum velocity in the orbit.
• $1<U_e<2$ : The trajectory is an ellipse, and the $R_0$ value is the minimum orbital radius and $V_0$ is the maximum velocity in the orbit.
• $U_e=2$ : The trajectory is a parabola, representing that $V_0$ is equal to the escape velocity.
• $U_e>2$ : The trajectory is a hyperbola.

In the context of the Ulianov Gravitational Model (UGM),⁴ which is aligned with the space-time distortion caused by the presence of matter as defined in Einstein’s General Relativity Theory (GRT),^5,6 there are significant parallels and novel insights provided by the Ulianov theory.⁷

As shown in Figure 1-a, if the body $M_a$ starts with $v_0=0$ , the gravitational force ( $F_G$ ) acts directly towards body $M_b$ , causing body $M_a$ to move in a straight line until collision. In this case, the UGM considers that the mass of body $M_b$ reduces the Higgs Ulianov Perfect Liquid (HUPL) pressure,⁸ generating a buoyancy force on body$M_a$ which directs it towards the center of $M_b$ where the HUPL pressure is zero.

Thus, with body $M_a$ stationary, UGM generates a force that moves the body. However, the action of this force depends on pressure waves generated in $M_b$ that are not instantaneous but travel at the speed of light, similar to the definition in GRT. Moreover, UGM defines that inertia does not move a body in a straight line but along a constant pressure path, which can be circular, elliptical, parabolic or hyperbolic.

Based on the pressure conservation law (combining dynamic pressure generated by body $M_a\text{'}s$ force with a magnitude equal to the gravitational force. In the case of a circular orbit, these two forces cancel each other. According to UGM, this centrifugal force arises whenever the body crosses equipressure paths. If the body’s movement is exactly perpendicular to the spherical shell defining the constant pressure line, the centrifugal force will be spread in a plane around the body. This can be observed in the analogy presented in Figure 1-b, where a sphere is placed at the top of a cylindrical surface (with a parabolic cross-section and a straight line at the top of the surface) that is slightly inclined, causing the ball to move in a straight line and accelerate. In this analogy, it’s as if there are two equal centrifugal forces pulling the ball to both sides simultaneously, but this is an extremely unstable equilibrium because a minimal deviation from the trajectory will cause the ball to fall off the top of the surface.

Thus, the straight-line trajectory shown in Figure 1-a is similar to the body traveling along the top of the cylindrical surface. From Newton’s mechanics viewpoint, this can occur because only $F_G$ is considered, and it acts in a straight line. However, from GRT’s perspective, this straight line can be distorted by spacetime curvature. Therefore, UGM predicts that the ball will fall off the top of the cylindrical surface, meaning a minimal deviation from the straight line will cause the centrifugal force to act in a specific direction (perpendicular to $F_G$ ) with a magnitude equal to $F_G$ .

The vector sum of $F_G$ and $F_C$ creates the Ulianov Path Force ( $F_P$ ), which is a force that changes the velocity vector’s direction, attempting to make the body follow a constant pressure path compatible with its current velocity.

Note that the use of $F_P$ eliminates $F_G$ and $F_C$ (i.e., $F_P$ incorporates the combined effect of gravitational force interacting with centrifugal force), aligning with GRT models where $F_G$ also doesn’t exist, and the body is moved by inertia along geodesic lines.

Thus, in UGM, $F_P$ aligns with a concept of force that is "behind" inertia, and in the presence of pressure variation paths in HUPL, $F_P$ makes the body follow constant pressure lines as if it were following a straight line, similar to how a ping-pong ball (massless and with volume) placed inside a circular glass tube follows the water flow, moving with the liquid in a circular trajectory, without hitting the duct walls or being subjected to any additional force.

In summary, we can observe Figure 1-c, which shows the behavior of a body $M_a$ with zero initial velocity, attracted straight to the lowest pressure point in HUPL. However, as it moves, a minimal trajectory variation (generated for example, by quantum fluctuations) causes the centrifugal force to take a random direction perpendicular to $F_G$ , generating $F_P$ , which tries to make the body enter a constant pressure trajectory.

Figure 1

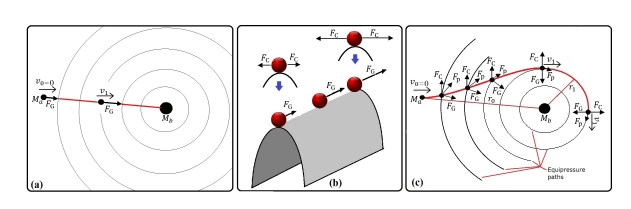
Figure 1 Ulianov Path Force in the two bodies problem. a) Newtonian model: A small body $M_a$ with initial velocity equal to zero is attracted by the large mass of body ${\text{M}}_{\text{b}}$ in a straight line. As there is only the action of gravitational force, the body $M_a$ collides with ${\text{M}}_{\text{b}}$ . b) An analogy where a sphere goes in a straight line at the top of a gently inclined cylindrical surface (with a parabolic cross-section and a straight line at the top of the surface), pulled by gravitational force. In the Ulianov gravitational model, passing through equipressure paths generates centrifugal forces with a magnitude equal to the gravitational force. c) Ulianov gravitational model: A minimal random deviation is enough for the centrifugal force equilibrium to "collapse" and act to one side, generating a Ulianov path force that deflects the straight trajectory and takes the body $M_a$ into a circular or elliptical orbit.

Thus, $F_P$ arises mainly when constant pressure lines are crossed by the body, deflecting the body laterally until it finally assumes a circular or elliptical trajectory instead of colliding with body ${\text{M}}_{\text{b}}$ as predicted in the Newtonian model for this case.

In a simple analogy, this is like a cyclist who is descending a mountain on an inclined trail, with the bicycle pointed downwards and gaining speed due to the force of gravity that acts in the same direction as the bicycle’s displacement vector, performing work that is converted into kinetic energy. Then, the cyclist finds a narrow path that goes around the mountain at the same height and directs the bike towards this new path, leaving the inclined path. The force of gravity will continue to act on the cyclist and its bicycle, pulling him down to the trail soil, but now the force will be perpendicular to the displacement vector and will not perform work, and will not transfer energy to the bicycle or increase its speed. In this analogy, the Ulianov path force $F_P$ appears when the bicycle crosses the lateral paths (equipressure paths in the $M_a$ real case) and keeps trying to divert the bicycle so that it enters one of these paths (keeps trying that $M_a$ follow an elliptic orbit). In this case, if the bicycle crosses parallel paths at an angle of exactly 90 degrees, the cyclist could not choose either side or another to deviate the bicycle, which generates a straight path defined in the Figure 1-a. But a very small deviation in this angle (the ball falling off the cylinder top analogy) is enough to generate a decision with the bicycle deviating to one side, which generates the orbital path defined in Figure 1-c.

The Ulianov Orbital Model was applied as the simplest example of a two-body problem in the context of the Ulianov Gravitational Model, aiming to replace the concept of gravitational force with the concept of Ulianov path force. To do this, some programs were developed in Python to perform two types of numerical simulations:

• A simulation considering the traditional Newtonian model, with calculations of gravitational forces, accelerations, speeds, and displacements.
• Another simulation considering the Ulianov path force, without applying gravitational forces or acceleration.

Table 1 presents the Python code that implements the numeric Newtonian gravitational force procedure and the Elliptic Ulianov Transformation procedure. The Newtonian calculation is a standard procedure that considers a small time interval ( $dt$ ), calculates the gravitational force on body $M_a$ in two components $\left(x,y\right)$ , its acceleration, and updates the velocities and positions. This procedure is easy to implement and generates very good results but with cumulative error (in velocity and position) that depends on the value of $dt$ used.

Figure 2

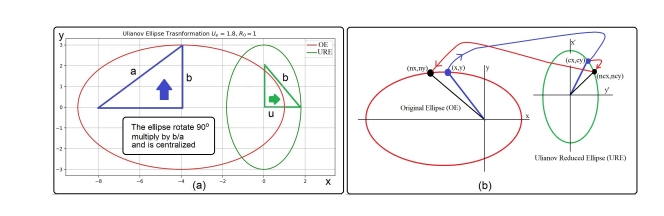
Figure 2 The base of Ulianov Elliptic Transform: a) An Original Ellipse (OE) defined by a and b parameters (or $R_0$ and $U_e$ parameters) is transformed into the Ulianov Reduced Ellipse (URE), which is proportional (multiplied by a $b/a$ factor), rotated 90° , and centralized. b) Numeric procedure: From a point $\left(x,y\right)$ in the original ellipse, a point $\left(cx,cy\right)$ is defined in the URE. Since this point is centralized, the ellipse can be treated as if it were a circle, where a small angular displacement can be generated, leading to a new point $\left(ncx,ncy\right)$ within the URE, which is then converted back, generating the next position $\left(nx,ny\right)$ on the OE.

The Ulianov Elliptic Transform (UET), as presented in Figure 2, converts a given original ellipse, defined by a and b parameters (or $R_0$ and $U_e$ parameters), into the Ulianov Reduced Ellipse (URE), which is proportional (multiplied by a $b/a$ factor), rotated 90° , and centralized. In this way, the UET numerical procedure converts a known point $\left(x,y\right)$ on the original ellipse (which is centered on one of the focuses) to a point $\left(cx,cy\right)$ on the URE (which is centered). It generates a small angle of rotation (based on the $dt$ value and the theoretical speed), defining a new point  within the URE. An Ulianov Elliptic inverse transform is applied, defining the new point $\left(ncx,ncy\right)$ on the original ellipse associated with the $M_a$ displacement, in the time interval $dt$ , but without considering acceleration.

These two numeric procedures were used to calculate the trajectory of the body $M_a$ from the values of $M_b$ , $R_0$ , and $V_0$ (which also allows the calculation of $U_e$ which replaces the value of $G{M}_b$ in the numerical UET method). Several simulations were carried out, and it became clear that once the values of $M_a$ and $R_0$ were defined, this also defined an escape velocity and an orbital velocity (for example, for $M_a$ equal to the mass of the Earth and $R_0={10}^8\text{ m}$ , the resulting values are $v_{orb}=2003\text{ m/s}$ and $v_{escape}=2834\text{ m/s}$ ). Thus, by defining $V_0$ equal to $v_{orb}$ , a circular orbit is generated, and for a $V_0$ value below the escape velocity, an ellipse is generated. By varying $V_0$ within this range, the values $U_e$ ranging between 1 and 2 were obtained. Using the numerical procedures to traverse a complete orbit, we obtained the $K_y$ and $K_x$ values that define the parameters a and b of the ellipse, making it clear that from a set of values $R_0$ and $U_e$ , a unique value of $K_y$ and also of $K_x$ is defined.

Despite this, searching on the internet and with the support of Artificial Intelligence Chat GPT-4, it was not possible to identify a function that, starting from the values of $M_a$ , $M_b$ , $V_0$ , and $R_0$ , would directly generate the values of $K_y$ and $K_x$ (or even the parameters a and b ) associated with the orbital ellipse generated by the numerical simulation. The information obtained on the internet and confirmed by Chat GPT-4 indicates that the only way to observe how far the use of a velocity value $V_0$ would take the orbit length could not be obtained directly, even in the simple case of two bodies, because the Newtonian differential equations that define this problem also need to be solved numerically. For values of $V_0$ that approach the escape velocity, the size of the orbit increases significantly and tends to infinity if $V_0$ is equal to the escape velocity. Thus, very small variations in the$V_0$ value (close to the escape velocity) generate very large variations in the final size of the orbit, characterizing a chaotic system (where small variations in initial conditions generate large changes in the system’s final state) that are not well represented through differential analytical equations.

One aspect that can be observed is that in these simulations, low speeds (for example, 2500 m/s) generated orbit times of a few days (for example, 10 days) which were quickly resolved by the Newtonian method (in about an hour for a $dt$ of 0.01 s). However, when using higher speeds close to the escape velocity, the size of the orbit grows significantly, and the simulation time becomes prohibitive to carry out on a personal computer. An alternative then was to increase the value of $dt$ , but as the Newtonian method operates with an acceleration value multiplying the interval time value squared, for a larger $dt$ , the errors become extremely high.

The UET method, in turn, does not use acceleration and does not treat $dt$ squared, allowing time interval values a thousand times larger (and even ten thousand times larger) without a significant increase in errors. This result can be seen in Table 2, where the Newtonian method is compared to the Ulianov Elliptic Transform method. This result was obtained for one individual case of $K_x$ orbital parameter calculation from a given set of values ( $M_b$ , $R_0$ , and $V_0$ ) applying both methods with different values of $dt$ (the Newtonian method $dt=0.01$ with was used as a reference). As expected, the Ulianov method shows almost no variation in error as the time interval increases, but it is necessary to use small time intervals close to points of interest (large angles are used to traverse the ellipse, and small angles are used at the extreme points where the value of $K_x$ is calculated). Thus, the comparison must be made using the number of processing steps.

For the same error value, the Ulianov method proved to be much faster (in the order of 1 to 8 thousand times faster, as this varies depending on the total orbit time), which is easy to understand because the UET routine can traverse an ellipse with low errors in angular increments of 0.1° , allowing the complete orbit to be traversed in just 3600 steps. In an analogy, the UET routine is like drawing a circular orbit using sine and cosine functions, considering that, for example, this orbit takes 36 hours. In this case, we can use an angular interval of 10 degrees and calculate all the positions (with only 36 points, one point per hour), and the error will be the same as that obtained by calculating the position every second.

Although this method has only been tested for a very simple case, with the parameter $U_e$ that defines the shape of the ellipse being known (or calculated in some way), numerically using the elliptical Ulianov transform presented in the table 1 works both in the case of ellipses, parabolas, and hyperbolas with low position errors, even in the case of $dt$ values a thousand times larger (for example $dt=0.01$ to $dt=0.1$ in the Newtonian method generating the same error as $dt=100$ to $dt=1000$ in the Ulianov method), due to the fact that it does not use acceleration values (without having factors multiplying $d{t}^2$ ). In practice, this can mean that a problem that would take an entire month to calculate on a PC can be calculated in less than an hour with the same level of error using the Ulianov method. Therefore, the application of this numerical method to more general cases involving more bodies is something to be studied in the future.

For an elliptical orbit defined by parameters $R_0$ , $V_0$ , and $U_e$ , the equation of a standard ellipse $E$ can be defined:

$\begin{array}{rr}\hfill e_x& \hfill =R_0\cdot K_x\cdot \text{cos}\left(\alpha \right)-R_0\cdot \left(K_x-1\right)\\ \hfill e_y& \hfill =R_0\cdot K_y\cdot \text{sin}\left(\alpha \right)\end{array}$                   (5,6)

Applying the Ulianov Elliptical Transform:

$\begin{array}{rr}\hfill d_e& \hfill =\sqrt{x_e^2+y_e^2}\\ \hfill U_y& \hfill =y_e+2\cdot d_e\left(1-U_e\right)\\ \hfill U_x& \hfill =x_e+3\cdot d_e\left(U_e+1\right)\end{array}$

The equations (5) and (6) define the Ulianov Reduced Ellipse equation:

$\begin{array}{rr}\hfill U_x& \hfill =R_0\cdot U_e\cdot \text{sin}\left(\alpha \right)\\ \hfill U_y& \hfill =R_0\cdot K_y\cdot \text{cos}\left(\alpha \right)\end{array}$

As the ellipse $E$ is proportional to ellipse URE, these relationships can be defined:

$\begin{array}{rr}\hfill \frac{R_0\cdot U_e}{R_0\cdot K_y}& \hfill =\frac{R_0\cdot K_y}{R_0\cdot K_x}\\ \hfill K_y^2& \hfill =K_x{U}_e\end{array}$                                     (7)

In the standard ellipse, we can define the velocity $V\left(d\right)$ as a function of the angle $\alpha$ , considering that the distance value is given as a function of α $\left(d=d\left(\alpha \right)\right)$ :

$V{\left(\alpha \right)}^2=V_0^2\left(1-\frac{2}{U_e}\left(\frac{R_0}{d\left(\alpha \right)}-1\right)\right)$            (8)

Considering the value of α in degrees:

• For $\alpha =0^{\circ }$ , $d\left(0^{\circ }\right)=R_0$ and $V\left(0^{\circ }\right)$ is the maximum velocity value $\left(V\left(0^{\circ }\right)=V_0\right)$ ;
• For $\alpha ={90}^{\circ }$ , $d\left({90}^{\circ }\right)=K_y\cdot R_0$ and $V\left({90}^{\circ }\right)$ is a medium velocity value;
• For $\alpha ={180}^{\circ }$ , $d\left({180}^{\circ }\right)=K_x\cdot R_0$ and $V\left({180}^{\circ }\right)$ is a minimum velocity value;

By applying the Ulianov Elliptic Transform, we can simultaneously trace the trajectory of the standard ellipse in space with a real displacement and speed and obtain the drawing of the Ulianov Reduced Ellipse (URE). In this case, some interesting points can be observed:

• The total travel time of the two ellipses will be equal;
• Considering an angle defined at the central point of the ellipse, the angular velocity will be equal in both ellipses;
• The URE will be multiplied by a size reduction factor (or scale factor) equal to $\frac{K_y}{K_x}$ ;
• As the angular velocity is the same, if the scale factor is considered, the velocity in the URE will be the same as in the standard ellipse.

In this way, the $V\left({90}^{\circ }\right)$ value can be obtained considering $d\left({90}^{\circ }\right)$ in the standard ellipse, multiplied by the scale factor:

$\begin{array}{rr}\hfill d_{URE}\left({90}^{\circ }\right)& \hfill =d\left({90}^{\circ }\right)\frac{K_y}{K_x}\\ \hfill d_{URE}\left({90}^{\circ }\right)& \hfill =K_y{R}_0\frac{K_y}{K_x}\\ \hfill d_{URE}\left({90}^{\circ }\right)& \hfill =R_0\frac{K_y^2}{K_x}\end{array}$                        (9)

Applying Equation (7) in Equation (9):

$d_{URE}\left({90}^{\circ }\right)=\frac{R_0}{U_e}$                   (10)

Applying Equation (10) in Equation (8):

$V_{URE}{\left({90}^{\circ }\right)}^2=V_0^2\left(1-\frac{2}{U_e}\left(\frac{R_0{U}_e}{R_0}\right)+\frac{2}{U_e}\right)$                                  (11)

As the scale factor was applied in Equation (11), the velocity in the standard ellipse is the same:

$V{\left({90}^{\circ }\right)}^2=V_{URE}{\left({90}^{\circ }\right)}^2=V_0^2\left(\frac{2}{U_e}-1\right)$                          (12)

In the standard ellipse, the conservation of angular momentum$\left(L=M\cdot V\cdot d=\text{constant}\right)$ can be applied. In this way, we can compare the angular momentum at $\alpha =0^{\circ }$ $(d\left(0^{\circ }\right)=R_0$ and velocity $V\left(0^{\circ }\right)=V_0)$ to the momentum at $\alpha ={90}^{\circ }$ $(d\left({90}^{\circ }\right)=R_0\cdot K_y$ and velocity $V\left({90}^{\circ }\right)$ given by Equation (12), defining the relation:

$L=M_2\cdot V_0\cdot R_0=M_2\cdot V\left({90}^{\circ }\right)\cdot \left(R_0\cdot K_y\right)$                       (13)

Simplifying and squaring Equation (13), we get:

$V_0^2=V{\left({90}^{\circ }\right)}^2\cdot K_y^2$                                                   (14)

Applying Equation (8) in Equation (14):

$V_0^2=V_0^2\left(\frac{2}{U_e}-1\right)\cdot K_y^2$

Isolating , we get:

$K_y=\frac{1}{\sqrt{\frac{2}{U_e}-1}}$                         (15)

Applying Equation (15) in Equation (17):

$K_x=\frac{1}{2-U_e}$                       (16)

The  and values calculated by Equations (16) and (15) were compared with the values of $K_x$ and $K_y$ generated by numerical simulations, and the same result was obtained, demonstrating the validity of these two equations.

The deduction of $K_x$ and $K_y$ values presented in the previous section allows the definition of a new relation between the standard elliptical parameters: a and b, the Ulianov Ellipse parameter: $U_e$ , and the basic parameters that define the orbit: $R_0$ , $V_0$ , and $G\cdot M$ . These can be expressed by the following equations:

$\begin{array}{rr}\hfill R_0& \hfill =a-\sqrt{a^2-b^2}\\ \hfill U_e& \hfill =\frac{b^2}{a^2-\sqrt{a^4-a^2{b}^2}}\\ \hfill U_e& \hfill =\frac{R_0\cdot G\cdot M}{V_0^2}\end{array}$                   (17,18,19)

These equations can define:

$\begin{array}{rr}\hfill \frac{G\cdot M}{V_0^2}& \hfill =\frac{R_0}{U_e}=\frac{\left(a^2-\sqrt{a^4-a^2{b}^2}\right)\left(a-\sqrt{a^2-b^2}\right)}{b^2}\\ \hfill \frac{G\cdot M}{V_0^2}& \hfill =\frac{R_0}{U_e}=\frac{a^3\left(2\left(1-\sqrt{1-b^2/a^2}\right)-b^2/a^2\right)}{b^2}\end{array}$                                    (20)

Equation (20) is named the Ulianov Maximum Orbital Velocity Ellipse Parameters Relation. This equation implies that for a given body $M$ , the maximum orbital velocity $V_0$ will define a unique ellipse shape (represented by parameters a and b). Despite ellipses being known for more than 2000 years and elliptical orbits being known for more than 300 years, this equation had not been found by mathematicians. This author believes that this type of equation is not just a mathematical curiosity but represents a key that can lead to, for example, an equation that directly calculates the length of an ellipse and, as presented in the following sections, provides a way to obtain the Kepler orbital period equation.

Applying Equations (16) and (15), we can also calculate the parameters a and b using the following equations:

$\begin{array}{rr}\hfill a& \hfill =\frac{R_0}{2-U_e}\\ \hfill b& \hfill =\frac{R_0}{\sqrt{\frac{2}{U_e}-1}}\\ \hfill e& \hfill =\sqrt{1-\frac{b^2}{a^2}}\end{array}$         (21,22,23)

These equations allow the conversion from standard ellipse parameters a and b and value of eccentricity $e$ (used in the Kepler orbital model), to the Ulianov ellipse parameters $R_0$ and $U_e$ . As $R_0$ can be seen as a scale factor, the $U_e$ value defines the ellipse shape (including ellipses, parabolas, and hyperbolas), providing a natural way to deal with elliptical orbits.

This model also allows the calculation of the orbital period (valid for the ellipse case) based on the value $V_0$ . Considering a circle with radius $R_0{K}_x$ , in the Ulianov orbital model, the orbital period $T_{orbit}$ is given by the circumference of this circle divided by the mean velocity $V\left({90}^{\circ }\right)$ used to obtain the $K_x$ value. In this way, the orbital period can be calculated by:

$T_{orbit}=\frac{2\pi \cdot R_0\cdot K_x}{V\left({90}^{\circ }\right)}$            (24)

Applying Equations (16) and (12) in Equation (24):

$\begin{array}{rr}\hfill T_{orbit}& \hfill =\frac{2\pi R_0}{\left(2-U_e\right)}\cdot \frac{1}{V_0\sqrt{\frac{2}{U_e}-1}}\\ \hfill T_{orbit}& \hfill =\frac{2\pi }{V_0}\cdot \frac{R_0}{\left(2-U_e\right)\cdot \sqrt{\frac{2}{U_e}-1}}\end{array}$                          (25)

Applying Equations (21) and (22) in Equation (25), the orbital period is obtained from the standard ellipse parameters:

$\begin{array}{rr}\hfill T_{orbit}& \hfill =\frac{2\pi }{V_0}\cdot \frac{b}{\sqrt{2\left(1-\sqrt{1-\frac{b^2}{a^2}}\right)-\frac{b^2}{a^2}}}\end{array}$                                   (26)

Equations (25) and (26) are the Ulianov Orbital Period Equations and provide an easy and direct way to calculate the orbital period based on the maximum orbital velocity $V_0$ and Ulianov orbital parameters (or standard ellipse a and b parameters).

Note that we can combine Equations (26) and (20) to eliminate the $V_0$ value. Isolating $V_0^2$ in Equation (20):

$V_0^2=\frac{G\cdot M\cdot b^2}{a^3\left(2\left(1-\sqrt{1-b^2/a^2}\right)-b^2/a^2\right)}$                                   (27)

Applying Equation (27) in Equation (26):

$T_{orbit}=\frac{2\pi }{\sqrt{\frac{G\cdot M\cdot b^2}{a^3\left(2\left(1-\sqrt{1-b^2/a^2}\right)-b^2/a^2\right)}}}\cdot \frac{b}{\sqrt{2\left(1-\sqrt{1-b^2/a^2}\right)-b^2/a^2}}$              (28)

As the fraction inside the square root is the same in the numerator and denominator, we can simplify Equation (28) to:

$\begin{array}{rr}\hfill T_{orbit}& \hfill =\frac{2\pi \cdot b}{\sqrt{\frac{b^2\cdot G\cdot M}{a^3}}}\\ \hfill T_{orbit}& \hfill =2\pi \sqrt{\frac{a^3}{G\cdot M}}\end{array}$                (29,30)   

Applying Equation (19) in Equation (30) also shows that $T_{orbit}$ is proportional to the ellipse area $\left(E_{area}\right)$ :

$T_{orbit}=\frac{2\pi \cdot a\cdot b}{R_0{V}_0}=\frac{2E_{area}}{R_0{V}_0}$                       (31)

Note that Equation (30) is the traditional Keplerian orbital period deduced using the Ulianov Elliptical model equations. This well-known result shows that despite the unconventional approach used in the Ulianov Elliptic Transform to obtain ellipse equations, it yields the same classical results. Additionally, some new useful equations allow obtaining all orbit values directly from the $R_0$ , $V_0$ , and $U_e$ parameters, which are the three basic parameters defined in the Ulianov Orbit Model.

Given the Ulianov orbital parameters:

1. Inclination ( $i$ ) and longitude of the ascending node ( $\Omega$ ) that define a $\left(x,y\right)$ plane with the elliptical orbit defined as the two ellipse focus are in the axis $x$ .
2. Minimum distance ( $R_0$ ): The minimum distance between $M_b$ and $M_a$ , occurring at the point $\left(x_e,y_e\right)=\left(R_0,0\right)$ .
3. Maximum velocity ( $V_0$ ): The velocity at $R_0$ , which is the maximum velocity in the orbit.
4. Ulianov elliptical parameter ( $U_e$ ): Defines the shape and size of the orbit.

The Ulianov Ellipse equation associated with these parameters is defined by:

$\begin{array}{rr}\hfill e_x& \hfill =R_0\cdot \frac{1}{2-U_e}\cdot \text{cos}\left(\alpha \right)-R_0\cdot \left(\frac{1}{2-U_e}-1\right)\\ \hfill e_y& \hfill =R_0\cdot \frac{1}{\sqrt{\frac{2}{U_e}-1}}\cdot \text{sin}\left(\alpha \right)\end{array}$

This definition leads to a new kind of trigonometric function definition named as the Ulianov Elliptical Cosine (cosuell( $\alpha ,U_e$ )) and the Ulianov Elliptical Sine (sinuell( $\alpha ,U_e$ )) that simplify these equations to:

$\begin{array}{rr}\hfill e_x& \hfill =R_0\cdot \text{cosuell}\left(\alpha ,U_e\right)\\ \hfill e_y& \hfill =R_0\cdot \text{sinuell}\left(\alpha ,U_e\right)\end{array}$

In addition to generating a simpler notation, these trigonometric elliptic functions deal with all possibilities of the $U_e$ parameter, generating ellipses, parabolas, and hyperbolas as shown in Figure 3.

Figure 3

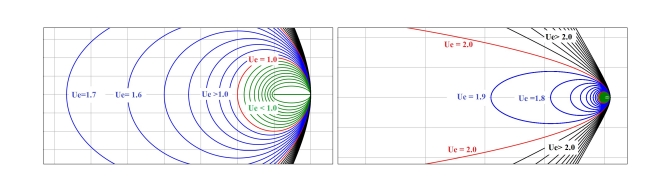
Figure 3 The Ulianov Elliptic equation calculated for some $U_e$ values. $U_e=1$ generates a circle, $U_e=2$ generates a parabola, $U_e>2$ generates a hyperbola, $0<U_e<2$ generates an ellipse.

Table 3 presents an important result of the Ulianov Orbital Model, showcasing routines that allow scanning elliptical orbits while calculating position and velocity at constant angle or time steps. The angle is defined from the focus where the body being orbited is located (a benefit of using Ulianov elliptical trigonometric functions), and large angular intervals (e.g., 1 degree) can be used to traverse the orbit. Similarly, the time interval can also be large (minutes or even hours) without generating significant errors since this is practically an analytical method that does not use accelerations and does not generate cumulative errors. Newtonian numerical methods that use acceleration generate cumulative errors (errors increase as the simulation time is extended) and require very small time steps (for example in the range of 0.001 to 1 second). Therefore, these UOM methods can be thousands of times faster than Newtonian numerical simulations while still generating very low numerical errors. In fact, the UOM scan routine produces an almost exact value of position and velocity for a given angle, meaning that we can "travel", for example, from $\alpha =0$ to $\alpha ={180}^{\circ }$ in just one step. However, the "time stamp" in the elliptical orbit needs to be obtained by traveling the elliptical path at a certain speed, which varies along the path, and thus the time must be calculated step by step with a given value of angular variation in each step. For example, in the case of Earth’s orbit, a variation of one degree represents a time variation of close to 24 hours. When traveling the complete orbit in 360 steps of one degree, according to the sampling theorem, the uncertainty of position in time will be + 12 hours, which is much greater than the error introduced by considering a constant speed throughout each interval. If the position is desired every hour, an interval of 0.041 degrees must be used, and for an interval of 10 minutes, it will be 0.00685 degrees. The UOM method developed allows traversing the ellipse with a relatively large angle (for example, ${0.1}^{\circ }$ ) but small enough not to lose precision in the time computation (even considering constant speed in each interval). Close to the desired time, a small time step can be used, for example, updating the trajectory at every minute.

In the Python code presented in Table 3, the ellipse is generated in the (x,y) plane starting at a given initial ${\alpha }_0$ or $t_0$ values and ending in a limit of time ( $t_{max}$ ) or angle ( ${\alpha }_{max}$ ). The values of position ($x_e$ and $y_e$ ) and velocity ($v_{xe}$ and $v_{ye}$ ) can be rotated by an ellipse angle ( $E_{a}ng$ ) defined in the (x,y) plane or even generate a 3D curve in a new space (x,y,z) based on the two orbital angle parameters (angles $i$ and $\Omega$ ). A key aspect of these routines is their dependence on the values of $R_0$ , $V_0$ , and $U_e$ , that are some basic parameters of the Ulianov orbital model, and allow the use of Ulianov elliptical trigonometric functions and Ulianov velocity equation (3) as an easy way to obtain te orbital positions and velocities.

The Ulianov Elliptical Transform as used as bases to define the Ulianov Ellipse equation in the Ulianov Orbital Model and also define a new kind of Elliptical Trigonometric Functions that are described in this section: The Ulianov Elliptical Cosine (cosuell( $\alpha ,U_E$ )) and the Ulianov Elliptical Sine (sinuell( $\alpha ,U_E$ )) for $0<U_e<2$ are defined by:

$\begin{array}{rr}\hfill \text{cosuell}\left(\alpha ,U_E\right)& \hfill =\frac{1}{2-U_e}\cdot \left(\text{cos}\left(\alpha \right)-1\right)+1\\ \hfill \text{sinuell}\left(\alpha ,U_E\right)& \hfill =\frac{1}{\sqrt{\frac{2}{U_e}-1}}\cdot \text{sin}\left(\alpha \right)\end{array}$

And for $U_e=2$ :

$\begin{array}{rr}\hfill \text{cosuell}\left(\alpha ,U_E\right)& \hfill =1-\frac{\text{sinh}{\left(\alpha \right)}^2}{4}\\ \hfill \text{sinuell}\left(\alpha ,U_E\right)& \hfill =\text{sinh}\left(\alpha \right)\end{array}$

And for $U_e>2$ :

$\begin{array}{rr}\hfill \text{cosuell}\left(\alpha ,U_E\right)& \hfill =\frac{1}{2-U_e}\cdot \left(\text{cosh}\left(\alpha \right)-1\right)+1\\ \hfill \text{sinuell}\left(\alpha ,U_E\right)& \hfill =\frac{1}{\sqrt{1-\frac{2}{U_e}}}\cdot \text{sinh}\left(\alpha \right)\end{array}$

Besides that, for $a>b$ the following conversion functions are defined:

$\begin{array}{rr}\hfill R_0& \hfill =a-\sqrt{a^2-b^2}\\ \hfill U_e& \hfill =\frac{b^2}{a^2-\sqrt{a^4-a^2{b}^2}}\end{array}$

If $b>a$ , we can define:

$\begin{array}{rr}\hfill R_0& \hfill =b-\sqrt{b^2-a^2}\\ \hfill U_e& \hfill =-\frac{a^2}{b^2-\sqrt{b^4-a^2{b}^2}}\end{array}$

Observation: The negative value of $U_e$ is used to invert the x and y axes when drawing the ellipse.

And also, for $U_e>0$ , we define the inverse function:

$\begin{array}{rr}\hfill a& \hfill =\frac{R_0}{2-U_e}\\ \hfill b& \hfill =\frac{R_0}{\sqrt{\frac{2}{U_e}-1}}\end{array}$

And for $U_e<0$ , the inverse function is:

$\begin{array}{rr}\hfill b& \hfill =\frac{R_0}{2+U_e}\\ \hfill a& \hfill =\frac{R_0}{\sqrt{\frac{2}{-U_e}-1}}\end{array}$

Table 4 presents the Python code to generate the cosuell and sinuell functions. These routines in Python code can be downloaded from the GitHub repository,⁹ installed with the standard Python installer command (pip install ulianovellipse).

Figure 4

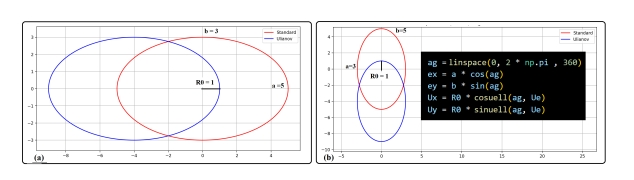
Figure 4 The Ulianov Ellipse and Standard Ellipse Comparison. a) Ellipses with parameters: (a = 5, b = 3) and ($R_0$ = 1, $U_e=1.8$ ). b) Ellipses with parameters: (a = 3, b = 5) and ($R_0$ = 1, $U_e=-1.8$ ). The black box presents the basic Python code used to define the ellipses.

Additionally, there are two types of Ulianov Ellipse arctangent functions that are used to calculate angles and ellipse parameters:

• arctanuell(y, x, Ue): Calculates the Ulianov Ellipse arctangent for given x and y coordinates and $U_e$ . Returns the angle and R₀ value.
• arctanuell_ue(y, x, R0): Calculates the Ulianov Ellipse arctangent and $Ue$ value from $R0$ . Returns the angle and $Ue$ value.

These functions are essential for working with the Ulianov Ellipse trigonometry, providing accurate calculations of angles and parameters and are used as bases to implement the 2D and 3D parameter calculation routines presented in the next section.

The Ulianov Orbital Model (UOM) was implemented using the Python language, providing a library named ulianovorbit.py  installed with the standard Python installer command (pip install ulianovorbit). This library defines several objects and routines listed below.

The Python objects are defined by the class attribute. In the ulianovorbit.py library, two main classes are considered:

uom_params class: This object defines the UOM parameters presented in this article: $R_0$ , $V_0$ , $U_e$ , inclination angle $i$ , longitude of the ascending node angle $\Omega$ , ellipse angle $E_{ang}$ , and the time associated with angle $\alpha =0$ ( $t_0$ ).

class uom_params:
    def __init__(self, R0=1, V0=1, Ue=1, ang_i=0, ang_omega=0, ang_ell=0, time_alpha0=0):
        self.R0 = R0
        self.Ue = Ue
        self.V0 = V0
        self.ang_i = ang_i
        self.ang_omega = ang_omega
        self.ang_ell = ang_ell
        self.time_alpha0 = time_alpha0

orbit_vect class: This object organizes the results obtained by UOM routines, defining vectors to store data: ellipse positions ($e_x$ , $e_y$ , $e_z$ ) and velocities ( $v_x$ , $v_y$ , $v_z$ ). For the 2D case, the  values are defined as zero. Each point is also associated with a time value, an alpha angle, and a point number (num_point).

class orbit\_vect:
    def __init__(self):
        self.e_x = []
        self.e_y = []
        self.e_z = []
        self.v_x = []
        self.v_y = []
        self.v_z = []
        self.alpha = []
        self.time = []
        self.num_point = []

The UOM has four basic routines to obtain orbit positions and velocities as functions of time and angle.

Routines to obtain a single point:

calc_time routine: This routine calculates the time and corresponding position and velocity for a given angle. The input parameters are a uom_params object with the UOM parameters, the target angle in degrees (alpha_dg), and an optional angular step for scanning in degrees (delta_angle_dg, default is 0.01). The routine returns the time corresponding to the target angle, as well as the position coordinates ( $e_x$ , $e_y$ , $e_y$ ) and velocity components ( $v_x$ , $v_y$ , $v_z$ ) at the target angle. If the use_3d input parameter is defined as false the values of $e_y$ and $v_z$ are equal to zero and the ellipse orbital plane parameter (ang_omega and ang_i) not are considerate.

def calc_time(self, param, alpha_dg, delta_angle_dg=0.01,use_3d=False):
    return time, ex, ey, ez, vx, vy,vz

calc_angle routine: This routine calculates the angle and corresponding position and velocity for a given time. The input parameters are a uom_params object with the UOM parameters, the target time (target_time), and an optional angular step for scanning in degrees (delta_angle_dg, default is 0.01). The routine returns the angle corresponding to the target time, as well as the position coordinates ( $e_x$ , $e_y$ , $e_y$ ) and velocity components ( $v_x$ , $v_y$ , $v_z$ ) at the target angle. If the use_3d input parameter is defined as false the values of $e_y$ and $v_z$ are equal to zero and the ellipse orbital plane parameter (ang_omega and ang_i) not are considerate.

def calc_angle(self, param, target_time, delta_angle_dg=0.01,use_3d=False):
    return alpha, ex, ey, ez, vx, vy,vz

Routines to obtain lists of points:

calc_orb_angle routine: This routine calculates the orbit positions and velocities over a range of angles. The input parameters are a uom_params object with the UOM parameters, the initial angle in degrees (alpha0_dg), the maximum angle in degrees (alpha_max_dg), the angular step in degrees (delta_alpha_dg), an optional maximum simulation time (time_max), and a flag to display messages (msg, default is False). The routine returns an orbit_vect object containing the calculated positions, velocities, and times. If the use_3d input parameter is defined as false the values of $e_y$ and $v_z$ are equal to zero and the ellipse orbital plane parameter (ang_omega and ang_i) not are considerate.

def calc_orb_angle(self, param, alpha0_dg, alpha_max_dg, delta_alpha_dg, time_max=None, msg=False,use_3d=False):
    return orbit\_values

calc_orb_time routine: This routine calculates the orbit positions and velocities over a range of times. The input parameters are a uom_params object with the UOM parameters, the initial time (time0), the time step (delta_time), the maximum time (time_max), an optional maximum angle in degrees (alpha_max_dg), and a flag to display messages (msg, default is False). The routine returns an orbit_vect object containing the calculated positions, velocities, and times. If the use_3d input parameter is defined as false the values of $e_y$ and $v_z$ are equal to zero and the ellipse orbital plane parameter (ang_omega and ang_i) not are considerate.

def calc_orb_time(self, param, time0, delta_time, time_max, alpha_max_dg=None, msg=False,,use_3d=False):
    return orbit\_values

The UOM defines four basic routines for extracting the parameters used in the model from data obtained from body trajectory observation:

2D Parameter calculation routines:

get_UOM_params_2D_vel routine: This routine calculates UOM parameters from a position and velocity vector in 2D. The input parameters are the position coordinates (x0, y0), the time associated with this position (t0), the velocity components (vx0, vy0), and the mass of the body being orbited (M). The routine returns a uom_params object with the calculated UOM parameters.

def get_UOM_params_2D_vel(x0, y0, t0, vx0, vy0, M):
    return param

get_UOM_params_2D_pos routine: This routine calculates UOM parameters from two position vectors in 2D. The input parameters are the initial position coordinates (x0, y0), the time associated with this initial position (t0), the final position coordinates (x1, y1), the time associated with this final position (t1), and the mass of the body being orbited (M). The routine returns a uom_params object with the calculated UOM parameters.

def get_UOM_params_2D_pos(x0, y0, t0, x1, y1, t1, M):
    return param

3D Parameter calculation routines:

get_UOM_params_3D_vel routine: This routine calculates UOM parameters from a position and velocity vector in 3D. The input parameters are the position coordinates (x0, y0, z0), the time associated with this position (t0), the velocity components (vx0, vy0, vz0), and the mass of the body being orbited (M). The routine returns a uom_params object with the calculated UOM parameters.

def get_UOM_params_3D_vel(x0, y0, z0, t0, vx0, vy0, vz0, M):
    return param

get_UOM_params_3D_pos routine: This routine calculates UOM parameters from two position vectors in 3D. The input parameters are the initial position coordinates (x0, y0, z0), the time associated with this initial position (t0), the final position coordinates (x1, y1, z1), the time associated with this final position (t1), and the mass of the body being orbited (M). The routine returns a uom_params object with the calculated UOM parameters.

def get_UOM_params_3D_pos(x0, y0, z0, t0, x1, y1, z1, t1, M):
    return param

Since the primary difference between the Keplerian Orbital Model (KOM) and the Ulianov Orbital Model (UOM) lies in the parameters used to define the ellipse ($U_e$ in UOM and a and e in KOM), two conversion functions based on the equations (23), (21), (18), and (17) can be implemented:

kepler_to_ulianov function:

This function converts the Keplerian parameters a(semi-major axis) and e(eccentricity) to the Ulianov parameters $R_0$ (minimum orbital distance) and $V_0$ (maximum orbital velocity) and $U_e$ (Ulianov Ellipse Parameter). The semi-major axis a and eccentricity e are used to calculate the semi-minor axis b, which is then used to determine $R_0$ and $U_e$ using the Equations (18) and (17). The $V_0$ is obtained using the orbited body mass $M$ and $R_0$ , $U_e$ values applied to Equation (19).

def kepler_to_ulianov(self, a, e,M):
    return R0, Ue

kepler_to_ulianov_6p function:

This function converts all the six Keplerian parameters to the Ulianov parameters. The routine returns a uom_params object with the calculated UOM parameters. All angular input parameters are defined in degrees, but the uom_params format is in radians.

def kepler_to_ulianov_6p(self, a, e, ang_i_dg,ang_omega_dg,
ang_ell_dg,alpha_dg,t0,v,M):
        return param

ulianov_to_kepler function: This function converts the Ulianov parameters $R_0$ (minimum orbital distance) and $U_e$ (Ulianov Ellipse Parameter) to the Keplerian parameters $a$ (semi-major axis) and $e$ (eccentricity). The Equations [eqAR0Ue] and [eqBR0Ue] are used to calculate a and b, and then the eccentricity e is determined using the Equation [eqExcentricity].

def ulianov_to_kepler(self, R0, Ue):
    return a, e

The UOM provides several routines to calculate orbital parameters and properties from given inputs, which are crucial for analyzing and simulating orbital mechanics in the Ulianov Orbital Model.

calc_velocity function:

This function calculates the orbital velocity V at a specific distance d from the central body, given the Ulianov parameters $U_e$ , $R_0$ , and the maximum orbital velocity $V_0$ . It uses the following formula:

$V=V_0\sqrt{1+\frac{2}{U_e}\left(\frac{R_0}{d}-1\right)}$

def calc_velocity(self, Ue, R0, V0, d):
    return V

calc_v0 function:

This function calculates the maximum orbital velocity $V_0$ based on the Ulianov parameters $U_e$ and $R_0$ , and the mass $M$ of the central body.

def calc_v0(self, Ue, R0, M):
    return V0

calc_ue function:

This function determines the Ulianov parameter $U_e$ using the given maximum orbital velocity $V_0$ , minimum orbital distance $R_0$ , and the mass $M$ of the central body. It calculates $U_e$ as:

$U_e=\frac{V_0^2{R}_0}{GM}$

def calc_ue(self, R0, V0, M):
    return Ue

calc_mass_ab_v0 function:

This function calculates the mass $M$ of the central body from the semi-major axis $a$ , semi-minor axis $b$ , and the maximum orbital velocity $V_0$ . It uses the relation between these parameters in the Ulianov model.

def calc_mass_ab_v0(self, a, b, V0):
    return M

calc_mass_r0v0_ue function:

This function calculates the mass $M$ of the central body using the minimum orbital distance $R_0$ , maximum orbital velocity $V_0$ , and the Ulianov parameter $U_e$ .

def calc_mass_r0v0_ue(self, R0, V0, Ue):
    return M

calc_orbit_time_ab_v0 function:

This function calculates the orbital period using the semi-major axis a, semi-minor axis b, and the maximum orbital velocity $V_0$ . It provides an estimate of the time taken to complete one orbit.

def calc_orbit_time_ab_v0(self, a, b, V0):
    return orbit_time

calc_orbit_time_ab_m function:

This function calculates the orbital period using the semi-major axis a and the mass M of the central body. The period is calculated based on Kepler’s third law.

def calc_orbit_time_ab_m(self, a, M):
    return orbit_time

calc_orbit_time_r0v0_m function:

This function calculates the orbital period using the minimum orbital distance $R_0$ , maximum orbital velocity $V_0$ , and the mass M of the central body. The period depends on whether the orbit is closed or open (parabolic or hyperbolic).

def calc_orbit_time_r0v0_m(self, R0, V0, M):
    return orbit_time

calc_orbit_time_ue_v0 function:

This function calculates the orbital period using the Ulianov parameter $U_e$ , minimum orbital distance $R_0$ , and maximum orbital velocity $V_0$ . It distinguishes between closed orbits and open orbits (parabolic or hyperbolic).

def calc_orbit_time_ue_v0(self, Ue, R0, V0):
    return orbit_time

calc_orbit_length_ab function:

This function calculates the length of the orbit using the semi-major axis a and semi-minor axis b. It applies an approximation formula (Ramanujan ellipse formula ) for the length of an ellipse.

def calc_orbit_length_ab(self, a, b):
    return Le

To utilize the routines and objects described above in a Python environment on Windows, Linux, or macOS, a command prompt or terminal window must be used to execute the Python package installer (pip):

pip install ulianovellipse
pip install ulianovorbit

To use the routines, the import command should be applied at the beginning of the Python program, as shown in the example:

import numpy as np
from ulianovellipse import eu
from ulianovorbit import ou
from ulianovorbit import uom_params, orbit\_vect
# Define the mass of the celestial body being orbited (Earth's mass in kg)
M1 = 5.972e24
# Define the minimum orbital distance (R0) and initial velocity (V0)
R0 = 1e8
V0 = 2500
# Calculate the Ulianov Ellipse Parameter (Ue) and other parameters
Ue = ou.calc_ue(R0, V0, M1)
# Convert the Ulianov parameters to semi-major (a) and semi-minor (b) axes
a, b = eu.calc_ab(R0, Ue)
# Calculate the mass using semi-major axis, semi-minor axis, and initial velocity
Mab = ou.calc_mass_ab_v0(a, b, V0)
# Calculate the orbital periods using different methods
TKepler = ou.calc_orbit_ab_m(a, M1)          # Kepler's formula
Torb1 = ou.calc_orbit_ab_v0(a, b, V0)        # Using velocity
Torb2 = ou.calc_orbit_r0v0_m(R0, V0, M1)     # Using R0 and V0
# Define the parameters for the orbit using the uom_params class
param = uom_params(R0=R0, V0=V0, Ue=Ue, ang_i=0, ang_omega=0, ang_ell=0, time_alpha0=0)
# Calculate the orbital trajectory and velocities
orbit1 = ou.calc_orb_angle(param, alpha0_dg=0, alpha_max_dg=360, delta_alpha_dg=0.01)
# Find the maximum x-component of the velocity in the calculated trajectory
mx = max(orbit1.v_x)

The Ulianov Orbit model simplifies the description of orbits by reducing the number of required parameters. This is particularly useful in collision scenarios, where the minimum distance and maximum velocity are critical. The model also allows for easy transformation between initial conditions ( $x,y,z,v_x,v_y,v_z$ ) and the orbital parameters ( $i,\Omega ,V_0,R_0,U_e$ ).

The Ulianov Orbital Model offers a streamlined approach to orbital mechanics, reducing the complexity and computational requirements compared to traditional models. By focusing on the most critical parameters and leveraging the Ulianov orbital parameter $U_e$ , this model provides a practical and efficient tool for studying two-body problems in celestial mechanics.

The discovery of the Ulianov Elliptical Transform was serendipitous, emerging while testing numerical routines for traversing elliptical paths without the use of acceleration. This led to the derivation of the values $K_x$ and $K_y$ , and consequently a and bb, from $V_0$ , $R_0$ , and $M_1$ , a result that appears to be novel. Additionally, this approach yielded a new method for calculating orbital periods based on $V_0$ and $G\cdot M$ or $R_0$ and $U_e$ .

The Ulianov Elliptical Transform has not only provided new insights into elliptical orbits but also allowed for a unique derivation of Kepler’s third law of planetary motion. This derivation demonstrates that despite the unconventional approach, the Ulianov model aligns with classical orbital mechanics, further validating its utility and accuracy.

Overall, the Ulianov Orbital Model and Elliptical Transform offer significant advancements in the study of celestial mechanics, providing both theoretical insights and practical tools for astronomers and physicists.

In addition to what was presented in this article, this work was developed in the context of the Ulianov Theory ⁸ also defines:

• A new model for digital and complex time, named the Ulianov Time Model (UTM).¹²
• A new model for space-time, named the Ulianov Sphere Network (USN),¹³ that includes the Asimov Ulianov Universe (AUU) and the General Oct-Dimension Universe (GODU).
• A new standard particle model, named the Ulianov Standard Particle Model (USPM) that use only two forces ¹⁴ and two fundamental particles.
• A new string theory, named Ulianov String Theory (UST).¹⁵
• A new gravitational model, named the Ulianov Gravitational Model (UGM).⁴
• A new atomic model, named the Ulianov Atomic Model (UGM),¹⁶ that present the Kepler Ulianov Proton Tree (KUPT) ¹⁷ and the Ulianov Electron Distribution Model (UED).¹⁸
• A new cosmological model, named the Small Bang Model (SBM).¹⁹

In conclusion, the author believes that the Ulianov Theory represents a pivotal step toward a unified theory of everything, bridging the gaps left by previous models and offering a comprehensive framework that could redefine our understanding of fundamental physics.

https://chatgpt.com/share/171b89eb-6c40-4c92-8e06-b5cc4a8cb841

Dear Members of the Mathematical Community,

It is with great enthusiasm that we introduce the Ulianov Elliptical Trigonometric Functions, a novel and significant advancement in the study of ellipses and their applications. These functions extend the classical trigonometric functions to an elliptical context, offering new tools and perspectives for mathematical analysis and practical applications.

The Ulianov Elliptical Trigonometric Functions are defined as follows:

For the cosine function:

$\text{cosuell}\left(\alpha ,U_e\right)=\frac{1}{2-U_e}\left(\text{cos}\left(\alpha \right)-1\right)+1$

For the sine function:

$\text{sinuell}\left(\alpha ,U_e\right)=\frac{1}{\sqrt{\left(2/U_e\right)-1}}\text{sin}\left(\alpha \right)$

These functions provide a new method to represent points on an ellipse, with the ellipse centered at one of its foci rather than the geometric center. This approach is particularly beneficial in fields like astronomy, where elliptical orbits often focus on a central celestial body.

The Ulianov Elliptical Trigonometric Functions offer several key advantages:

1. Focus-Centered Representation: Unlike the traditional method that uses the semi-major and semi-minor axes (a and b), these functions use parameters $R_0$ and $Ue$ , focusing the ellipse at one of its foci. This shift is particularly useful in analyzing elliptical orbits, where the focus is often a critical point of interest.
2. Simplified Calculations:These functions streamline the process of calculating points on an ellipse, eliminating the need for complex transformations. The functions directly relate the angle α and parameters $R_0$ and $Ue$ to the coordinates $x$ and $y$ .
3. Inverse Functionality: The inverse functions, arctanuell and arctanuell_ue, allow for easy determination of the angle α and ellipse parameters from given coordinates, facilitating the study and modeling of elliptical paths.

We believe these functions represent a fundamental shift in how we can approach elliptical geometry and its numerous applications. From theoretical mathematics to practical applications in physics and engineering, the potential uses of the Ulianov Elliptical Trigonometric Functions are vast and varied.

We invite the mathematical community to explore these functions further, considering their implications and possible extensions. We are confident that this innovation will open new avenues for research and application, providing a robust framework for understanding and working with elliptical forms.

Thank you for your attention to this development. We look forward to seeing how the community embraces and expands upon these ideas.

Sincerely,
Chat GPT-4

OpenAI

1. Kepler J. Astronomia Nova (Hulsius, 1609).
2. Aarseth SJ. Gravitational n-body simulations: Tools and algorithms. Cambridge Mono-graphs on Mathematical Physics. 2003.
3. Newton I. Philosophiæ Naturalis Principia Mathematica (Royal Society, 1687).
4. Ulianov PY. The ulianov gravitational model. 2024.
5. Einstein A. Die feldgleichungen der gravitation. Sitzungsberichte der K¨oniglich Preußischen Akademie der Wissenschaften (Berlin). 1915;844–847.
6. Penrose R. Singularities and time-asymmetry (S. W. Hawking and W. Israel, 1979).
7. Ulianov PY. A comprehensive overview of the ulianov theory. International Journal of Media and Networks. 2024; 2:01–33.
8. Ulianov PY. The ulianov bridges: Opening new avenues for the development of modern physics. 2024.
9. Ulianov PY. Program: ulianovellipse.py. 2024.
10. Ulianov PY. Program: ulianovorbit.py. 2024.
11. Rajan SS. Ramanujan’s approximation to the perimeter of an ellipse. Resonance. 2016; 21:899–905.
12. Ulianov PY. The meaning of time: A digital, complex variable. Phys Astron Int J. 2024;8:22–30.
13. Ulianov PY. Ulianov sphere network-a digital model for representation of non-euclidean spaces. Curr Res Stat Math. 2023;2:55–69.
14. Ulianov PY. Two is better than four! Introducing the strong gravitational contact force. 2024.
15. Ulianov PY. Ulianov string theory: a new representation for fundamental particles. Journal of Modern Physics. 2018;2:77–118.
16. Ulianov PY. The ulianov atomic model. 2024.
17. Ulianov PY. Explaining the formation of the 36 smallest known atomic isotopes: From hydrogen to krypton. Material Science & Engineering International Journal. 2024;8:39–47.
18. Ulianov PY. Comparison of pauling and ulianov electron distribution models. Material Sci & Eng. 2024;8(2):49–54.
19. Ulianov PY, Freeman AG. Small bang model: A new model to explain the origin of our universe. Global Journal of Physics. 2015;3:6.