In this paper we investigate the suspected effect of cosmic vacuum energy on the dynamics of cosmic space, while nevertheless still now the phenomenon of vacuum energy is not yet physically settled in a rigorous form. In view of what one needs for general relativistic approaches, we start here with considerations of the specific energy-momentum tensor of cosmic vacuum energy in the standard hydrodynamical form, and derive relations between vacuum energy density and vacuum pressure.  With the help of fundamental thermodynamic relations we then find relations of the two quantities, vacuum pressure and energy density, to the scale $R$ of the universe. These, however, allow for a multitude of power exponents $n$ , including the case of a constant vacuum energy density with $n=0$  and $R^n=const.$  Then we argue that for spaces of cosmic dimensions not only thermodynamical relations have to be fulfilled, but also, as we call them "gravodynamical relations", meaning that vacuum pressure has to work against the inner gravitational binding of space, mostly due to the gravitating masses distributed in this cosmic space. When we include this effect in addition to the thermodynamics we find that the vacuum energy density ${{\displaystyle \rho }}_{\Lambda }$ then can not anymore be considered as constant, but unavoidably as falling off with the scale of the universe according $R^{-2}$ . At the end of this article we then suspect, since vacuum energy even nowadays is not yet a physically well founded and understood quantity, that the Hubble expansion of the present universe is not driven by vacuum pressure, but by the change of gravitational binding energy at the ongoing structure formation of cosmic matter during the Hubble expansion.

1. Formulation of the thermodynamics and gravodynamics of empty space?

The question what means "empty space" - or synonymous for that - "vacuum" - has not yet been satisfactorily answered. In fact this question appears to be a very fundamental one which has already been put by mankind since the epochs of the greek natural philosophers till the present times of modern quantum field theoreticians. The changing opinions given as answers to this fundamental question over the changing epochs have been reviewed for example by Weinberg,¹ Overduin and Fahr² or Peebles and Ratra,³ but here we do not want to repeat all of these different answers that have been given in the past, we only at the begin of this article want to emphasize a few fundamental aspects of the present-day thinking with respect to the physical constitution of empty space.

Especially challenging in this respect is the possibility that empty space could despite of its conceptual "emptiness" - nevertheless unavoidably be "energy-loaded", perhaps simply as property of physical space itself. This strange and controversial aspect we shall investigate further below in this article. In a brief and first definition we want to denote empty space as a spacetime without any topified or localized energy representations, i.e. without energy singularities in form of point masses like baryons, leptons, darkions (i.e. dark matter particles) or photons, even without point-like quantum mechanical vacuum fluctuations. The latter condition, however, as stated by modern quantum theoreticians, anyway cannot be fulfilled, since vacuum fluctuations cannot be forbidden or be suppressed as learned from the basics of quantum mechanical principles.

If then nevertheless there should be a need to discuss that such empty spaces could be still energy-loaded, then this energy of empty space has to be seen as a pure volume-energy, somehow connected with the magnitude of the volume or perhaps with a scalar quantity of spacetime metrics, like for instance the global or local curvature of this space. In a completely empty space of this virtue, of course, no specific space points can be distinguished from any others, and thus volume-energy or curvature, if existent, are numerically identical at all space coordinates.

As it was shown by Fahr⁴ vacuum energy conservation can be formulated as constancy of the proper energy of a co-moving cosmic proper volume. Nevertheless an invariance of this vacuum energy per co-moving proper volume,${{\displaystyle e}}_{vac,}$ can of course only then be expected with some physical sense, if this quantity does not do any work on the dynamics of the cosmic geometry, especially by physically or causally influencing the evolution of the scale factor $R(t)$ of the universe.

If to the contrary, for example such a work in fact is done, and vacuum energy influences the dynamics of the cosmic spacetime (perhaps either by inflation or deflation), e.g. as in case of a non-vanishing energy-momentum tensor, then automatically thermodynamic requirements need to be respected and fulfilled, for example relating vacuum energy density and vacuum pressure by the standard thermodynamic relation.⁵

$\frac{d}{dR}({\epsilon }_v{}_{ac}{R}^3)=-p_v{}_{ac}\frac{d}{dR}{R}^3$

This above thermodynamic request is shown to be fulfilled by the following expression for the vacuum pressure

$p_{vac}=-\frac{3-n}{3}{\in }_{vac}$   (A)

Hereby the vacuum energy density itself is represented by a scale-dependence of the form ${\in }_{vac}\sim R^n$ . Then, however, it turns out that the above thermodynamic condition, besides for the trivial case $n=3$  when the vacuum does not at all act as a pressure (since the latter is vanishing according to Equ.(A); $p_{vac}(n=3)=0!)$ , is only non-trivially fulfilled for exponents $n\lessgtr 3$  , thus allowing also for $n=0$ , i.e. describing a constant vacuum energy density ${\in }_{vac}=const.$

2. Restricted vacuum conditions under gravitational selfbinding

A more rigorous and highly interesting restriction for exponent $n$    is, however, obtained after recognition that the above thermodynamic expression $(A)$ under large-scale cosmic conditions needs to be enlarged by a term representing the work that the expanding volume does against the internal gravitational binding of matter or vacuum energy in this volume. 

For mesoscale gas dynamics (like aerodynamics, meteorology etc.) this term does of course not play a role and can tacitly be neglected. On cosmic scales, however, there is a severe need to take into account this term. Under cosmic perspectives binding energy is an absolutely necessary quantity to be brought into the gravodynamical and thermodynamical energy balance of stellar matter, of interstellar cloud matter, or of cosmic matter. As worked out in quantitative terms by Fahr and Heyl,⁶ this then leads to the following more completed relation

$\frac{d}{dR}({\in }_{vac}{R}^3)=-p_{vac}\frac{d}{dR}{R}^3-\frac{8{\pi }^{2}G}{15c^4}\frac{d}{dR}[{({\in }_{vac}+3p_{vac})}^2{R}^5]$

where the last term on the right-hand side accounts for the internal, gravitational self-binding energy of the vacuum.

This completed equation describing the variation of the vacuum energy with the scale $\text{R}$  of the universe, as one can easily show, is again solved by the expression of the afore mentioned relation (A) : $p_{vac}=-\frac{3-n}{3}{\in }_{vac}$ , but now - different from before - leading to the following new requirement

$\frac{d}{dR}({\in }_{vac}{R}^3)=\frac{3-n}{3}{\in }_{vac}\frac{d}{dR}{R}^3\frac{8{\pi }^{2}G}{15c^4}\frac{d}{dR}[{\in }^2{}_{vac}{(n-2)}^2{R}^5]$  

Now, as one can see, in its above form, the upper, extended relation, however, is only fulfilled by the power exponent: $n=2!$ , - meaning that the corresponding cosmic vacuum energy density in order to meet the above requirements must vary - and needs to vary - like

${\in }_{vac}\sim R^{-2}$   (B)

This consequently furthermore means that, if it has to be consistently taken into account that vacuum energy acts upon spacetime both in a thermodynamical and gravodynamical sense, then the only reasonable assumption for the vacuum energy density is that drops off at the cosmic expansion inversely proportional to the square of the cosmic scale, i.e. ${\in }_{vac}={\in }_{vac,o}.{(R_0/R)}^2$ - rather than being a constant.^6,7 The question then, however, arises, how under these latter, new circumstances structure formation does influence the cosmic expansion, a problem recently discussed for the first time by Fahr⁸ and here, under the new auspices given now by relation  above, is taken up once again.

3. The evolution of the Hubble parameter

The above result unavoidably leads to the important question of what Hubble parameter $H=H(t)$  and what temporal change of it, i.e. $\text{dH}/\text{dt}$ ,  one has to expect as prevailing at the different cosmologic evolution periods or different world times $t$ . For Friedman-Lemaı̂tre-Robertson-Walker cosmologies (FLRW) the Hubble parameter $H(t)=\dot{R}(t)/R(t)$  generally is not a constant, but is given in form of the following differential equation (derived from the 1. Friedman equation; e.g.:^3-5

$H^2=\frac{{\dot{R}}^2}{R^2}=\frac{8\pi G}{3}[{\rho }_B+{\rho }_D+{\rho }_v+{\rho }_{\Lambda }]$  

where $G$  is Newton‘s gravitational constant, and ${\rho }_B,{\rho }_D,{\rho }_v,{\rho }_{\Lambda }$  denote the relevant equivalent cosmic mass densities of baryons, of dark matter, of photons, and of the vacuum energy.

In case that all of these quantities count at the same cosmologic period, then this complicates to find a closed solution for $H(t)$  and $R(t)$ over these cosmic times, because ${\rho }_B$ may vary proportional to $R^{-3}$ ,${\rho }_D$ most probably also according to $R^{-3}$ , but ${\rho }_v$ is generally thought to vary according to $R^{-4}$  (see Goenner, 1996, but also Fahr and Heyl, 2017, 2018).⁵ A solution for the Hubble parameter in this general case is shown in Figure 1 below.⁴  

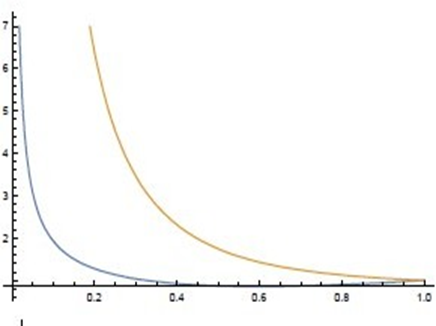
Figure 1 The Hubble Parameter H(x) (yellow curve) and the expansion velocity  (x) (blue curve) are shown as functions of the normalized Hubble scale x = R/R₀ on the basis of best-fitting values for ρ_m, ρ_d, ρ_v,.⁹

Amongst these quantities the cosmic vacuum energy density ${\rho }_{\Lambda }$ certainly is the physically least certain quantity, but on the other hand - if described with Einstein's cosmological constant $\Lambda ,$ then it represents a positive, constant energy density, i.e its mass equivalent ${\rho }_{\Lambda }$ in connection with a constant and positive vacuum energy density $\Lambda ,$ would consequently as well be a positive, constant quantity not dependend on the scale R or cosmic time t. This in fact would offer for the later phases of cosmic expansion, i.e. when at late times $t\ge t_0$ evidently ${\rho }_{\Lambda }\gg {\rho }_B,{\rho }_D,{\rho }_v,$ an easy and evident solution of the above equation for the late Hubble parameter $H=H(t\ge t_0)=H({\Lambda }_0)$ :

$H=H({\Lambda }_0)=\sqrt{\frac{8\pi G}{3}}{\rho }_{{\Lambda }_0}=const$

As support for this to be true already now it has been concluded from recent supernova SN1a redshift observations (Perlmutter, 2003, Riess et al., 1998, Schmidt et al., 1998)¹⁰ that in fact at the present cosmic era, most probably already sometimes ago, we were and are in a coasting, perhaps even an accelerated expansion phase of the universe.  

Now, however, when taking it further on serious that this is due to the term $\Lambda$ connected with cosmologic vacuum energy density ${\rho }_{\Lambda }$ , - however this time, not being a constant, but falling off like $R^{-2}$ ,  as discussed above in case the vacuum is thermodynamically and gravo dynamically active -, this then expresses the complicating fact that ${\rho }_{\Lambda }$ is not a constant anymore, but nevertheless sooner or later along the evolution of the universe at ongoing expansion must unavoidably become the dominant quantity in the universe amongst the other upper ingredients, i.e. ${\rho }_{\Lambda }\gg {\rho }_B,{\rho }_D,{\rho }_v,$ since falling off inversely proportional with $R$ , however, with the smallest power of ${(1/R)}^2$ .

Then in fact one will certainly also enter a cosmologic time with ${\rho }_{\Lambda }\gg {\rho }_B,{\rho }_D,{\rho }_{\nu }$  when the above differential equation for the Hubble parameter $H=H(t)$ can be written not in the earlier form given above, but nevertheless in an essentially simplified form, namely different from above, this time by:

$H=\frac{\dot{R}}{R}=\sqrt{\frac{8\pi G}{3}[{\rho }_B+{\rho }_D+{\rho }_v+{\rho }_{\Lambda }]}\simeq \sqrt{\frac{8\pi G}{3}[{\rho }_{\Lambda }(R)]}=\frac{R_0}{R}\sqrt{\frac{8\pi G}{3}{\rho }_{\Lambda ,0}}$

Under these new auspices of a thermodynamically reacting cosmic vacuum the expansion of the universe in this phase is then described by the above expression.

$\frac{\dot{R}}{R}=\frac{R_0}{R}\sqrt{\frac{8\pi G}{3}{\rho }_{\Lambda ,0}}$

with $R_0$  and $t_0$ denoting the present-day scale of the universe and the present cosmic time, and ${\rho }_{\Lambda ,0}$  denoting the equivalent vacuum mass density at this time $t_0$ . This, however, expresses the astonishing fact that from that time onwards into the future of the universe for $t\ge t_0$ the cosmic expansion will be characterized - neither by an acceleration nor by a deceleration -, but by a constant expansion velocity with $\ddot{R}=d\dot{R}/dt=0!$ , since:

$\dot{R}={\dot{R}}_0=R_0\sqrt{\frac{8\pi G}{3}{\rho }_{\Lambda ,0}}=const.$  

This means the cosmic expansion would naturally and necessarily sooner or later enter into a so-called "coastal" phase of the universal expansion. For such a coastal phase cosmologists since long ago were hunting (see e.g. Kolb,1989, Dev et al., 2001, Gehlaut et al., 2003),¹¹ and on the other hand were hoping for^12,13 to also fit distant supernovae-SN1a redshift measurements equivalently well as with "the accelerated universe" (Perlmutter et al., 1999, Schmidt et al., 1999, Riess et al., 1999).¹⁰

For that reason we shall now describe the Hubble parameter in the period $t\ge t_0$ at times with $1\ge H_0(t-t_0)$ finding:

$H(t\ge t_0)=\frac{R_0\sqrt{\frac{8\pi G}{3}{\rho }_{\Lambda 0}}}{R_0+{\dot{R}}_0(t-t_0)}=\frac{H_0}{1+H_0(t-t_0)}$  

where the Hubble parameter at time $t=t_0$  is denoted by $H_0=\sqrt{8\pi G{\rho }_{\Lambda 0}/3}$ . The important question then remains whether or not, even under these new perspectives, i.e of a "coastal cosmic expansion", the vacuum energy could still be understood as response to the change of negative gravitational binding energy of the universe connected with the ongoing expansion of matter in cosmic space, as demonstrated recently by Fahr?⁸

4. How operates a thermo-reactive vacuum under ongoing cosmologic structure formation?

Cosmic structure formation denotes the phenomenon of growing clumpiness of the cosmic matter distribution in cosmic space during the ongoing evolution of the expanding universe, i.e. the origin of larger and larger mass structures like galaxies, clusters or super-clusters of galaxies. Usually one does start cosmology with the assumption that at the beginning of cosmic time and the evolution of the universe cosmic space has a uniform deposition with matter and energy, justifying the use of the famous Robertson-Walker geometry. The question for the evolved universe then may arise whether or not the later cosmic expansion dynamics and the scale evolution $\dot{R}=dR/dt$ may perhaps be influenced by the ongoing structure formation, as it has to happen in order to create out of its earlier uniformity that hierarchically structured present-day universe manifest to us today?

The question now is whether this process of a structuration perhaps influences the ongoing Hubble expansion of the universe, perhaps either accelerating or decelerating, or stagnating its expansion with respect to the solutions of the standard Friedmann universe?⁵ This, however, could simply be due to the fact that under the new conditions of a self structuring cosmic matter the effective mass density ${\rho }_{eff}={\rho }_{eff}(t)$ of the universe does not behave like it normally does in a Friedmann universe like $\rho ={\rho }_0.{(R_0/R)}^3$ , but rather like ${\rho }_{eff}={\rho }_{eff,0}(t){(R_0/R)}^3$

The manifest universe, as it is, is not a homogeneous material structure, but stellar matter is distributed in space in form of galaxies, clusters of galaxies, and superclusters, i.e. it is structured in hierarchies. This can be described up to supercluster-scales by a point-related correlation function with an observationally supported correlation index of $\alpha =1.8$    ( see Bahcall and Chokski, 1992). This two-point correlation structure seen in cosmic galaxy distributions can be expressed through the underlying cosmic mass distribution given by an equivalent mass density of $\rho (l)={\rho }_{0,\alpha }.{(l/l)}^{-\alpha }$ .¹⁴

It is then most interesting to see from recent results by Fahr⁸ that the gravitational binding energy in this hierarchically structured universe, and its change with time, is described by a function ${\in }_{pot}={\in }_{pot}(R,\alpha )$ not only dependend on the outer scale $R=R(t)$ , but also on the correlation coefficient $\alpha =\alpha (t)$ of the structured cosmic matter in this cosmic system, namely given in the form:

${\in }_{pot}(R,\alpha )=\frac{{(4\pi )}^2(3-\alpha )}{9(5-2\alpha )}G{\overline{\rho }}^2{R}^5$

where obviously the permitted range of the structure coefficient is given by values $\alpha \le 2.5$ . Here $G$ is Newton‘s gravitational constant, and $\overline{\rho }=\overline{\rho }(R)$ denotes the average mass density in the associated, re-homogenized universe. It is interesting to recognize that for $\alpha =0$  (i.e. homogeneous matter distribution) in fact the potential energy of a homogeneously matter-filled sphere with radius $R$ is found, which does not vanish, but has a finite value, namely^6,7

${\in }_{pot}(\alpha =0)=\frac{{(4\pi )}^2}{15}G{\overline{\rho }}^2{R}^5$  

This latter binding energy, however, is fully incorporated by the Friedmann-Lemaı̂tre cosmology as the one normally reponsible for the deceleration of the "normal" Hubble expansion of the universe without the action the vacuum via .

${\rho }_{\Lambda }$  

If in contrast the cosmic deceleration turns out to be smaller than the "normal" Hubble deceleration or it even indicates an acceleration which normally is ascribed to the action of vacuum energy, then in our view this must be ascribed to the increased production of binding energy due to the upcome of structure formation with cosmic time. That means what really counts is the difference $\Delta {\in }_{pot}={\in }_{pot}(\alpha )-{\in }_{pot}(\alpha =0)$ between a structured and an unstructured universe. The value ${\in }_{pot}(\alpha =0)$ hereby serves as reference value for that potential energy in the associated, re-homogenized universe. What really counts in terms of binding energy of a structured universe causing a deviation from the Friedmann-Lemaitre expansion of the universe is the difference $\Delta {\in }_{pot}$ between the structured and the unstructured universe, since evidently the unstructured universe has its own, but nonvanishing amount of binding energy. For general cases one therefore obtains:

$\Delta {\in }_{pot}(\alpha ,R)=\frac{{(4\pi )}^2(3-\alpha )}{9(5-2\alpha )}G{\overline{\rho }}^2{R}^5-\frac{{(4\pi )}^2}{15}G{\overline{\rho }}^2{R}^5=\frac{{(4\pi )}^2}{3}·[\frac{(3-\alpha )}{3(5-2\alpha )}-\frac{1}{5}]·G{\overline{\rho }}^2{R}^5$

The question now poses itself: Is the change of binding energy $\Delta {\in }_{pot}(\alpha ,R)$ per cosmic time t or scale increment dR balanced by a corresponding unphysical change in thermal energy $\Delta {\in }_{therm}(\alpha ,R)$ of normal cosmic matter?  This we shall investigate in the next section down here.

5. The thermal energy of cosmic matter in the expanding universe

Starting from the assumption that the cosmic dynamics can be represented by a Hubble expansion with a Hubble parameter $H=\dot{R}/R$ it can be shown^4,8,15,16 that cosmic gases subject to such an expansion undergo a so-called Hubble drift in velocity space while moving with their own velocities  from place to place. This unavoidable Hubble drift $v{}_H=-v\cdot H$ will enforce the change per time of the velocity distribution function $f(v,t)$ of the cosmic gas atoms which is described by the following kinetic transport equation:

$\frac{\partial f}{\partial t}=vH·(\frac{\partial f}{\partial v})-H·f$   (40)

This above partial differential equation allows to derive the resulting distribution function $f(v,t)$ as function of the velocityand of the cosmic time $t$ , and as well its velocity moments, like e.g. the density $n(t)$ and the temperature $T(t)$ of the cosmic gas.

As it was shown already by Fahr,^15,16 the above kinetic transport equation does not allow for a solution in the form of a separation of variables, i.e. putting $f(v,t)=f_t(t)\cdot f_v(v)$ , but one rather needs a different, non-straight forward ad-hoc method of finding a kinetic solution of this above transport equation Equ.(40). It turns out that under the assumptions a): that at time $t=t_0$ a Maxwellian distribution $f(v,t{}_0)=Max(v,T_0)$ is valid, and b): that since that time a Hubble parameter $H(t)=H_0\cdot (1-(t-t_0))$ prevails like it was derived in the section before given by:

$H(t\ge t_0)=\frac{H_0}{1+H_0(t-t_0)}$  

with $H_0=\sqrt{8\pi G{\rho }_{\Lambda 0}/3,}$ ${\rho }_{\Lambda 0}$ denoting the equivalent mass energy density of the cosmic vacuum at the time $t=t_0$ , one can then write the actual distribution function at times $t\ge t_0$ , derived on the basis of the above partial differential kinetic equation, in the following form (see Fahr, 2021):

$f(v,t)=n_0\exp [-3H_0(t-t_0)\cdot \frac{{(1-H_0(t-t_0))}^3}{{\pi }^{3/2}{v}_0^3}\exp [-x^2\cdot {(1-H_0(t-t_0))}^2]$

where $v_0$ denotes the thermal velocity by $v_0^2=k{T}_0/m$ at the time $t_0$ , when a temperature $T(t_0)=T_0$ prevails. Hereby the normalized velocity coordinate x was introduced by $x=v/v_0$ . Furthermore it turns out that one can interprete the actually prevailing distribution function$f(v,t)$ as an actual Maxwellian with the time-dependent temperature $T(t\ge t_0)$ given by:

$T(t)=\frac{T_0}{{(1-H_0(t-t_0))}^2}$

and a time-dependent density

$n(t)=n_0\exp [-3H_0(t-t_0)]=n_0\cdot {(\frac{R(t)}{R_0})}^{-3}$

One therefore finds that under the given cosmologic prerequisites of a Hubble expansion with the Hubble parameter $H(t\ge t_0)$ the thermal energy ${\in }_{therm}$ of matter in this universe thus increases with time t like:

${\in }_{therm}=\frac{4\pi }{3}{R}^3\cdot n(t).(\frac{3}{2}kT(t))=\frac{4\pi }{3}\frac{(3/2)n_{0}k{T}_0{R}_0^3}{{(1-H_0(t-t_0))}^2}$

meaning that the total thermal energy of the matter in this whole Hubble universe apparently increases with the expansion - obviously violating standard thermodynamical principles according to which the temperature of matter decreases with the increase of cosmic space volume.

At this point of the argumentation Fahr^4,8 had recently developed a new idea to explain this mysterious, unphysical increase of the thermal energy on a physical basis: Namely he suspected that this increase in thermal energy of cosmic matter in this expanding universe is just compensated by the increase in negative-valued, cosmic binding energy $\Delta {\in }_{pot}(\alpha ,l_m)$ in case of a specific level of structure formation, measurable as a specific level of the correlation coefficient $\alpha (t)={\alpha }_0$ . The hope was that this negative binding energy is the genuine physical reason for the action of a so-called "vacuum pressure", corresponding to an equivalent mass density ${\rho }_{\Lambda }={\Lambda }_0{c}^2/8\pi G$ . Since we now have a new request derived in section 4 of how vacuum energy density should behave with the scale $R$ , this idea needs to be re-checked here putting the question whether or not this argumentation can still stand.

To pursue a little more this idea, we again start from the two competing quantities, i.e. the potential binding energy difference between the structured and the unstructured universe on one hand:

$\Delta {\in }_{pot}(\alpha ,R)=\frac{{(4\pi )}^2}{3}[\frac{(3/\alpha )}{3(5-2\alpha )}-\frac{1}{5}]G{\overline{\rho }}^2{R}^5$

and the thermal energy difference between the non-thermodynamical and the thermodynamical universe of cosmic matter on the other hand:

${\in }_{therm}=\frac{4\pi }{3}{R}^3\cdot n(t)\cdot (\frac{3}{2}kT(t))=\frac{4\pi }{3}(3/2)n_{0}k{T}_0{R}_0^3[\frac{1}{{(1-H_0(t-t_0))}^2}-1]$

Now, in order to guarantee energy conservation, we shall require that the change with cosmic time  of the first quantity $\Delta {\in }_{pot}(\alpha ,l_m)$ is equal to the negative change of the second quantity $\Delta {\in }_{therm}$ - a question that advices to specifically study the following quantity:

$\Delta \in ={\in }_{therm}-\Delta {\in }_{pot}(\alpha )=\frac{4\pi }{3}(3/2)n_{0}k{T}_0{R}_0^3[\frac{1}{{(1-H_0(t-t_0))}^2}-1]-\frac{{(4\pi )}^2}{3}[\frac{(3/\alpha )}{3(5-2\alpha )}-\frac{1}{5}]G{\overline{\rho }}^2{R}^5$  

In the following part we consider the times with $1\gg H_{\Lambda }(t-t_0)$ and describe the temporal evolution of the structure index $\alpha$ by: $\alpha (t)={\alpha }_0\exp [{\epsilon }_{\alpha }{H}_0(t-t_0)]$ with ${\epsilon }_{\alpha }\le 1$ . Then one can simplify the above expression into the form:

$\Delta \in (t)\simeq \frac{4\pi }{3}(3/2)n_{0}k{T}_0{R}_0^3[2H_0(t-t_0)]-\frac{{(4\pi )}^2}{3}[\frac{(3/{\alpha }_0[1+{\epsilon }_{\alpha }{H}_0(t-t_0)])}{3(5-2{\alpha }_0[1+{\epsilon }_{\alpha }{H}_0(t-t_0)])}-\frac{1}{5}]G{\overline{\rho }}^2{R}^5$

or furthermore - when identifying: $\frac{4\pi }{3}(3/2)n_{0}k{T}_0{R}_0^3={\in }_{therm,0}$ as the total thermal energy at time $t=t_0$ , and:

${(4\pi /3)}^{2}G{\overline{\rho }}^2{R}^5=G{M}_0^2/R_0={\in }_{tot,0}$ as the total binding energy at $t=t_0$ , one obtains:

$\Delta \in (t)\simeq {\in }_{therm,0}[2H_0(t-t_0)]-{\in }_{tot,0}[\frac{(3/{\alpha }_0[1+{\epsilon }_{\alpha }{H}_0(t-t_0)])}{(5-2{\alpha }_0[1+{\epsilon }_{\alpha }{H}_0(t-t_0)])}-\frac{3}{5}]$

First of all, the condition that the non-thermodynamical increase of the thermal energy ${\in }_{therm}$ in a universe with Hubble expansion is compensated just by the negative binding energy $\Delta {\in }_{pot}(\alpha ,R)$ of the structured mass in the universe can only be fulfilled, if this gravitational binding energy difference between the structured and the unstructured universe becomes negative. The required condition can in fact be fulfilled, if at the time t=t_0  the gravitational binding energy of the cosmic masses, i.e. ${\in }_{tot,0}={(4\pi /3)}^{2}G{\overline{\rho }}^2{R}^5=G{M}_0^2/R_0$ equals the actual thermal energy ${\in }_{therm,0}=\frac{4\pi }{3}(3/2)n_{0}k{T}_0{R}_0^3$ of the particles. This then leads to the following request:

$\Delta \in (t)/{\in }_0\simeq [2H_0(t-t_0)]-[\frac{(3/{\alpha }_0[1+{\epsilon }_{\alpha }{H}_0(t-t_0)])}{(5-2{\alpha }_0[1+{\epsilon }_{\alpha }{H}_0(t-t_0)])}-\frac{3}{5}]$

 What concerns the needed and necessary correlation coefficient $\alpha$ , one finds, however, as further restriction that only when this coefficient has attained a value of $\alpha \ge {\alpha }_c=1.5$ , then the resulting mathematical sign of ${\in }_{therm,0}$ allows a physical solution in the expected form (see our Figure 2 below).  This means that only when the structure formation process in the universe has progressed far enough, then the above required equality can in fact be achieved. But then, at times after that, when an accelerated expansion of the universe with a Hubble parameter $H=H_0$ prevails, then in fact the increase in negative potential energy of cosmic matter $\Delta {\in }_{pot}(\alpha ,R)$ is exactly balanced by the increase of thermal cosmic energy $\Delta {\in }_{therm}(R)$ . During this phase of the expansion of the universe one is obviously justified to assume that the creation of negative binding energy is the reason for the accelerated expansion of the universe, a phenomenon which in present-day cosmology is confidently always ascribed to the action of vacuum energy.

Figure 2 The quantity ϵ_pot(α) as a function of the correlation coefficient α.

In Figures 3 and 4 we show how the normalized total energy $\Delta \in (t)/\in {}_0$ varies with cosmic time t before and after the time t=t_0 demonstrating clearly how the actual correlation index $\alpha =\alpha (t_0)$ influences the situation. Though this clearly shows the importance of the actual correlation index, we at this point of the paper can not hide the fact that we actually do not have a clear description of the evolution of α and of the cosmic matter structure with world time $t$ . This is clearly appears as a point that remains to be theoretically derived in the upcoming time of cosmologic theory.

Figure 3 The quantity ϵ(t)/ϵ₀ is shown as function of x = H₀(t – t₀) from x=-0.5 to x=+0.5 for different correlation coefficients (from top to bottom):
α₁ = 2. 1; α₂ = 1. 8; α₃ = 1. 3

Figure 4 The loarithm Log (10, ϵ(t)/ϵ₀) is shown as function of x = H₀(t – t₀) from x=-0.5 to x=+0.5 for different correlation coefficients (from top to bottom):
α₁ = 2. 1; α₂ = 1. 8; α₃ = 1. 3

None.

None.

1. Weinberg S. The cosmological constant problem. Rev Mod Phys. 1989;61:1.
2. Overduin J, Fahr H J. Matter, spacetime and the vacuum. Naturwissenschaften. 2001;88:491–503.
3. Peebles PJE, Ratra B. The cosmological constant and dark energy. Rev Modern Physcs. 2003;75:559–599.
4. Fahr HJ. Determining the thermodynamics of cosmic gases at world times after the matter recombination, in: Research Trends and Challenges in Physical Sciences, B P International, Ed. S. Tüzemen, 2022a;8(8):83–100.
5. Goenner H. Einführung in die Spezielle und Allgemeine Relativitätstheorie, Spektrum Akademischer Verlag, Heidelberg–Berlin–Oxford, 1996.
6. Fahr HJ, Heyl M. Cosmic vacuum energy decay and creation of cosmic matter. Naturwissenschaften. 2007a.94:709–724.
7. Fahr HJ, Heyl M. Astron Nachr. 2007b;328(2):192–199.
8. Fahr HJ. How much could gravitational binding energy act as hidden cosmic vacuum energy. Adv Theo Comp Phy. 2022b;5(2):449–457.
9. Bennet CI, Halpern M, Hinshaw G, et al. First year of Wilkinson Anisotropy Probe (WMAP) observations. Astrophys Journal. 2003;Supplements:148(1):97–117.
10. Perlmutter S, Aldering G, Goldhabe G. The supernova cosmology project: Measurement of Omega and Lambda from 42 high–redshift supernovae. Astrophys J. 1999;517:565–586.
11. Kolb EW. A coasting cosmology. Astrophys J. 1989;344:543.
12. Cassado J, Jou D. Steady flow cosmological models. Astrophys Space Sci. 2013;344(2):513.
13. Cassado J. Linear expansion models versus standard cosmologies; a critical and historical overview. Astrophys Space Sci. 2020;365:16.
14. Fahr HJ, Heyl M. Stellar matter distribution with scale–invariant hierarchical structuring. Phys Astron Int J. 2019;3(4):146–150.
15. Fahr HJ. The thermodynamics of cosmic gases in expanding universes based on Vlasow–theoretical grounds. Adv Theo Comp Phy. 2021a;4(2):129–133.
16. Fahr H J. The baryon distribution function in the expanding universe after the recombination era. Phys Astron Int J. 2021b;5(2):37–41.