An attempt has been made to study the energy-spectrum of conduction electrons and the corresponding density-of-states (DOS) functions in semiconductors with the presence of electric and parallel magnetic fields. It is found for n-GaAs that the isotropic parabolic un-perturbed energy spectrum exhibits anisotropic dispersion with energy dependent mass anisotropy in the presence of an external electric field. This anisotropic dispersion relation transforms to an isotropic one under the approximation:$k_x^2\approx 1/3k^2;$ where $k_x$ also, the band-gap of semiconductor increases with both of electric and parallel magnetic fields. Is the x-component of wave-vector $\overline{k}$ . Furthermore, the carriers are disappeared from the conduction band-edge without oscillations in the case of only electric field. However, carriers vanish with oscillations with the presence of both the electric and magnetic fields. The well-known result of the DOS functions for parabolic band has been retrieved, under certain limiting conditions, from our generalized expressions. Our theoretical observations of band-gap enhancement and the DOS functions are correlated with the nature of the experimental findings.

Keywords: semiconductor, density of states, electric and parallel magnetic field, conduction band-age, parabolic band

DOS, density-of-states; VB, valence band; CB, conduction band; H, Hamiltonian

It was demonstrated that applying an external electric field, as a perturbation to a semiconductor, the bands are perturbed by the interaction of the electric field with the valence band (VB) and the conduction band (CB).¹ Therefore, the energy-spectrum of an electron in (CB) and hole in (VB) was modified with respect to un-perturbed bands. Accordingly, the basic characteristics of semiconductors such as density-of- state (DOS) functions, transport properties, etc. are influenced significantly² under different physical conditions. The importance of DOS has already been revealed by Landsberg.³The analytical formulations of various quantum processes of semiconductor, having different energy-band spectrum, are based on the DOS functions. Although, DOS functions have already been investigated extensively,^1,4 nevertheless it appears from the literatures survey that the electron energy-spectrum and the corresponding DOS have yet to be studied in semiconductors in the presence of an external electric and parallel magnetic fields.

In the present study, we describe a theoretical analysis on the electron energy-spectrum and corresponding DOS functions of a parabolic band semiconductor, in the presence of an externally applied electric field, $F\left(=\text{ef}\right),$ and a parallel magnetic fields, B(in Tesla). The present results are obtained by simply extending the same in the case of an electric field alone⁴ to the case of magnetic field, when the transverse component of the electron energy in the $E-\overline{k}$  dispersion relation is substituted by the quantizing energy⁵ due to Landau quantization. The present manuscript is arranged as the followings: in section 2, the theoretical back-ground followed by an electric field, applied along x-axis; in section 2B, the same energy–spectrum is extended to the cases of electric and a parallel magnetic fields, In section 2C, the DOS functions are derived for the above cases. In section 3, results are critically discussed based on our theoretical observations. Finally, in section 4, important conclusions are drawn based on our analyses.

Derivation of energy spectrum in presence of an external electric field

For an external electric field (f) applied along the x-axis, the perturbed Hamiltonian (H'), can be forwarded as  

$H\text{'}=F.x\mathrm{......}$   (1)

Where, $F=\text{ef}$ and e is the electron charge. The second order energy Eigen-value, $E_n^{\left(2\right)}\left(\overline{k}\right),$ under perturbation condition, Eqn (1) is given as⁶

$E_n^{\left(2\right)}\left(\overline{k}\right)=E_n\left(\overline{k}\right)+\langle n\overline{k}\left|H^{\prime }\right|n\overline{k}\rangle +\left\{{\left|\langle n\overline{k}\left|H^{\prime }\right|m\overline{k}\rangle \right|}^2\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$E_n\left(\overline{k}\right)-E_m\left(\overline{k}\right)$}\right.\right\}$   (2)

where, 

$H{\psi }_n\left(\overline{k},\overline{r}\right)=E.{\psi }_n\left(\overline{k},\overline{r}\right)$   (3)

$H=H_o+H\text{'}$   (4)

$H_o{u}_n\left(\overline{k},\overline{r}\right)=E_n\left(\overline{k}\right).u_n\left(\overline{k},\overline{r}\right)$   (5)

H is the total Hamiltonian, ${\psi }_n\left(\overline{k},\overline{r}\right)$  is the wave function with $u_n\left(\overline{k},\overline{r}\right)$  as the periodic function of it. $H_o$ , n, $\overline{r},\overline{k}$, E and $E_n\left(\overline{k}\right)$  are the un-perturbed Hamiltonian, the band index, the position vector of electron, the wave vector of the electron, the total energy of the electron and the energy of an electron in the periodic lattice, respectively. For a semiconductor having parabolic energy band, we get from Eqns (1) and (2)

$E_n^{\left(2\right)}\left(\overline{k}\right)=E_n\left(\overline{k}\right)-F\langle n\overline{k}\left|x\right|n\overline{k}\rangle +{\dot{F}}^2 {\{\left|\langle n\overline{k}\left|x\right|m\overline{k}\rangle \right|}^2\raisebox{1ex}{$$}\!\left/ \!\raisebox{-1ex}{$E_n\left(\overline{k}\right)-E_m\left(\overline{k}\right)$}\right.\}$  ……….. (6)

$u_{nm}(\overline{k)}=\langle n\overline{k}\left|x\right|m\overline{k}\rangle$  = …………. (7)

$=i{\displaystyle \int u_n}*.\frac{\partial }{{}^{\partial kx}}{u}_m\left(\overline{k},\overline{r}\right)d^{3}r$  ………….. (8)

Where $i=\sqrt{-1,k_x}$ is the x-component of $\overline{k}$ and the integration in Eqn (8) extends over the unit cell. From Eqns (6)-(8), with n-corresponding to conduction band $\left(n=c\right)$ and m, corresponding to valence band $\left(m=v\right),$  Eqns 6 can be reproduced as

$E_c^{\left(2\right)}\left(\overline{k}\right)=E_c\left(\overline{k}\right)-F.Xcc+F^2\frac{{\left|X_{cv}\right|}^2}{\left\{E_c\left(\overline{k}\right)-E_v\left(\overline{k}\right)\right\}}$  ……….. (9)

where,  $E_c\left(\overline{k}\right)=\frac{{\hslash }^2{k}^2}{2m_c}$ ……(10)

is the un-perturbed parabolic conduction band with  is the effective electron mass at the band-edge of the CB. $\hslash$  is the reduced Planck’s constant, given by $\hslash =h/2\pi$ . $X_{cc}$  and Xcv are the intra and interband transition matrix elements, respectively. For the evaluation of $X_{cc}$  and $X_{cv}$ , we use $\overline{k}$ . $\overline{p}$  Perturbation technique⁷ for the isotropic two-band model. The two-bands are separated by the energy gap, E_g at $\overline{k}=0$  accordingly, we find $X_{cc}=0$

$X_{cv}=\left[i \hslash E_g^{3/2}/\left(2m_m^{1/2}.\eta 2\right)\right].\frac{k_x}{R}$ ……….. (11)

$\eta =E_c\left(\overline{k}\right)-E_v\left(\overline{k}\right)={\left[E{g}^2+\frac{E_g{\hslash }^2{k}^2}{m_r}\right]}^{1/2}$  ………. (12)

and m_r is the reduced electron effective mass, given by

$m_r^{-1}=m_c^{-1}+m_v^{-1}$  ………….(13)

Combining the appropriate equations, the electron energy-spectrum in the presence of an external electric field, can be put forward, as.³

$\frac{k_x^2}{\left[2m_c^E/\hslash \{1+\varphi \left(E,F\right)\}\right]}+\frac{k_y^2}{2m_c^E/{\hslash }^2}+\frac{k_z^2}{2m_c^E/{\hslash }^2}=1$ ……… (14a)

where,

$\varphi \left(E,F\right)=[\frac{{\hslash }^2{F}^2}{4m_r{E}_g^{2}E}]*{\left[1+\frac{2m_c}{m_r}.\frac{E}{Eg}\right]}^{-5/2}$  ………… (14b)

Equations (14a) and (14b) show that in the presence of an external electric field, the isotropic parabolic un-perturbed energy-spectrum, (Eqn 10), exhibits an anisotropic dispersion relation, with energy dependent mass anisotropy in the presence of an external electric field. This anisotropic dispersion relation transform to an isotropic one under the approximation:

$k_x^2\approx 1/3k^2$ .……. (15)

Under this, Eqn (14a) turns out to the isotropic dispersion relation:

$E=\frac{{\hslash }^2{k}^2}{2m_c}+\frac{{\hslash }^2{F}^2{E}_g^3}{12m_r}.{\left[E_g^2+\frac{Eg.{\hslash }^2{k}^2}{m_r}\right]}^{-5/2}$  ……. (16)

Further, in the limiting case, when $\overline{K}\to 0,$  i.e; at the band-edge, Eqn(16) provides the results:

$\Delta E=\frac{{\hslash }^2{F}^2}{12m_r{E}_g^2}$  ……… (17)

From Eqn.17, it is clear that in the presence of an electric field, F, the conduction band-edge moves vertically up-word by an amount, ΔE. As a result, the band-gap of semiconductor is apparently increased by ΔE, when an external electric field is applied. This observation is opposite to the Franz⁸ and Keldysh⁹ effects, a phenomena where the band-gap decreases by means of an applied electric field. In support of our theoretical findings, the experimental observation of the band-gap enhancement with the electric field can be found in.^10–12

Derivation of energy-spectrum in presence of an electric and parallel magnetic fields

In the presence of a parallel magnetic field, B, applied along the direction of the electric field, the transverse component of electron energy, $E_t$  is quantized by Landau quantization⁵ as

$E_t\frac{{\hslash }^2{k}_{┴}^2}{2m_r}=\left(\text{J}+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)\hslash {\omega }_{cv}\pm \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.g\mu B .B$  …..(18)

Where, $K\perp$ is the transverse or normal component of wave vector, J is the Landau quantum number; $\hslash {\omega }_{cv}$ is cyclotron energy, given by

$\hslash {\omega }_{cv}=\hslash {\omega }_c+\hslash {\omega }_v$ ………(19)

and g is the difference in spin g-factors of conduction and valence band

and ${\mu }_B$ is the Bohr’s magnetron.

$g=g_c-g_v$ ………. (20)

Generally, the magnitude of the transverse component of electron energy, E is given as $E_t\ll E_g$ . Under this condition, we can approximate $k_x^2/ K^2\approx 1,$ in Eqn(11). Therefore, combining Equation (9)-(12), we can approximately write Eqn (16).

$\text{E=}\frac{{\hslash }^2{k}_x^2}{2m_c}+\frac{{\hslash }^2{k}_{\perp }^2}{2mc}+\frac{{\hslash }^2{E}_g^3{F}^2}{12m_r} {\left[E_g^2+\frac{Eg{\hslash }^2(k_x^2+k_{┴}^2)}{m_r}\right]}^{-5/2}$  + ……(21)

For $F\to 0,$  we find from Eqns (16) - (18)

$k_x^2 {\hslash }^2\approx 2m_c\left[\text{E-}\frac{m_r}{m_c}{E}_t\right]$  ……….. (22)

Combining Eqns (16), (18)-(21), we get

$\gamma \left(E,F\right)=\frac{{\hslash }^2{k}_x^2}{2m_c}+\frac{m_r}{m_c} \{\left(\text{J+1/2}\right)\hslash {\text{ω}}_{\text{cv}}\pm 1/2 g\mu B. B\}$  ……(23)

$\gamma \left(E,F\right)=E-\frac{{\hslash }^2{F}^2}{12m_r{E}_g^2} {\left[1+\frac{2m_c}{m_r}.\frac{E}{Eg}\right]}^{-5/2}$  .……..(24)

Equations (23) and (24) represent the E- k_x dispersion relation of conduction electron in presence of electric and parallel magnetic fields. From Eqns (23) and (24), we find that the parabolic energy-band no more remains to the parabolic shape but is quantized by means of electric as well as parallel magnetic fields. Under the limiting conditions, $k_x\to 0,$ we find from Eqn 21 the new increased band gaps $\Delta \left(\overline{E}\right)$  of semiconductor in presence of electric and parallel magnetic fields.

$\Delta \left(\overline{E}\right)= \frac{m_r}{m_c}{E}_t+\frac{{\hslash }^2{F}^2}{12m_r{E}_g^2} {\left[1+\frac{2Et}{E_g}.\right]}^{-5/2}$  ……..(25)

Under the case, when $B\to 0$ and $k_x\to 0,$

We find from Eqns (23)-(25), the increased band-gap $\Delta \left(\overline{E}\right)$  in presence of electric field only same as Eqn (17). Combining Eqns (17) and (25), we find that the increased band-gap value of semiconductor in the presence of electric field and a parallel magnetic field of greater that the value, when only electric field is present, i.e.,$\Delta \left(\overline{E}\right)>\Delta E.$  

Derivation of the density –of-states (DOS) functions in presence of electric as well as with the presence of electric and parallel magnetic fields

The density-of-states, N (E, F), in presence of electric field (F) can be written from Eqns. (14a) and (14b) as³

$N\left(E,F\right) =\frac{1}{2{\pi }^2}.{\left(\frac{2m_c}{{\hslash }^2}\right)}^{3/2}{E}^{1/2}{(1+\Phi (E,F))}^{-1/2}*\{1-1/3(E.\psi (E,F)/(1+\Phi (E,F)\}$ .………. (26)

Where

$\psi (E,F) = -\Phi (E,F)\{\left(1/E\right)+ \frac{5m_c}{m_r{E}_g} {\left[1+\frac{2m_c}{m_r}.\frac{E}{Eg}\right]}^{-1}\}$  ……………. (27)

In the absence of electric field, N (E, 0) assumes the well-known form,¹³ from Eqns. (26) and (27), as

$N\left(E\right)=\frac{1}{2{\pi }^2}.{\left(\frac{2m_c}{{\hslash }^2}\right)}^{3/2}{E}^{1/2}$ …….  (28)

Now, from Eqns (24) and (25), the density-of-states, N (E, F, B) in the presence of electric and parallel magnetic fields, is given as (for conduction band, CB)

$N\left(E,F,B\right)=\frac{1}{4{\pi }^2}.{\left(\frac{2m_c}{{\hslash }^2}\right)}^{3/2}\hslash {\text{ω}}_c{\displaystyle {\sum }_{J=0}^{J_{max}}\frac{\Phi \left(E,F\right)}{\sqrt{\gamma \left(E,F\right)-\frac{m_r}{m_c}{E}_t}}}$  ……..(29)

Where,

$\Phi \text{'}\left(E,F\right)=\frac{d\Phi \left(E,F\right)}{dE}=1+\frac{5}{1\dot{2}}\frac{mc}{m_r^{\dot{2}}}\frac{{\hslash }^2{F}^2}{E_g^3}{\left[1+\frac{2m_c}{m_r}.\frac{E}{Eg}\right]}^{-7/2}$  ….  (30)

$\hslash \text{ωc=}\frac{e\hslash B}{m_c}$ i.e. cyclotron of an energy spectrum an electron in the conduction band,

$J_{max}$ =Maximum value of Landau quantum number,

Integer value of $\gamma \left(E,F\right)/\hslash {\text{ω}}_{\text{c}}$

In the limiting case, when $F\to 0,$ Eqns (29 and 30) will lead to the well-known form for (CB) as¹³

$N\left(E,B\right)=\frac{1}{4{\pi }^2}.{\left(\frac{2m_c}{{\hslash }^2}\right)}^{3/2}\hslash \text{ωc}{\displaystyle {\sum }_{J=0}^{J_{max}}\frac{1}{{\left[E-\left(J+\frac{1}{2}\right)\hslash \text{ωc}\right]}^{-1/2}}}$ ……  (31)

Using the appropriate equations and taking n-GaAs as an example, together with the parameters,¹³ $E_g=1.424eV,m_c=0.063m_0,$  and $m_v=0.5m_0,T=300K,$ we have plotted the energy-spectrum versus electron wave-vector $\left(\overline{k}\right)$ shown in Figure 1, in the presence of electric field (f). This Figure 1 is plotted following Eqn. (16). The curve passes through origin, i.e., E=0 and $\overline{k}=0.$  This is the case of un-perturbed band. The amount of shift of the band-edge at $\overline{k}=0$ with electric field, $\left(f\ne 0\right)$ is given by Eqn. (17). Therefore, it is clear that the parabolic nature of the original band is modified to a large extent due to the electric field. It further appears that as the electric field is increased, the edge of the conduction band (CB) moves vertically in the positive energy direction. Consequently, the band-gap is increased with the electric field.

Franz⁸ and Keldysh⁹ effects, conventionally implies that the band-gap of a semiconductor decreases with the application of an electric field. Incidentally, in accordance with our calculations, Eqns (14a)-(17) and Figure 1, we observe that the Franz-Keldysh effects are directly the opposite one. The physical explanation in support of the above observation can be given, based on our works on optical absorption in the presence of an external electric field.¹²

Figure 1 Plots of Energy-Spectrum, E (in eV) against $\overline{k}$ (wave vector in atomic unit, 10⁸ cm^-1) for n-GaAs at 300K for f=0.0 V cm^-1 (dotted curve), $f_1=5\times {10}^{6}Vc{m}^{-1}$ and $f_2=1.0\times {10}^{7}Vc{m}^{-1}$ (solid line).

In Figure 2, we have plotted the electron energy- spectrum against wave-vector $k_x$ (in atomic unit) for the electric field, $\text{f}=0.0\left(Vc{m}^{-1}\right)$ and B=3.0 Tesla (dotted line); and $\text{f}=1.0\times {10}^{8}Vc{m}^{-1},B=3.0$ Tesla (Solid line); under extreme quantum limit, i.e., J=0. Figure 2 is plotted following Eqns (24) and (25). It is clear from Figure 2 that the dotted curve does not pass through origin; but shifting from it by an amount equal to (1/2) $\hslash {\text{ω}}_c.$  This shows that the band-gap increase with magnetic field, which is the well-known result. However, for the solid curve, the value of the electron energy (E) further increases with the electric field as well as magnetic fields. As we move deep into the band. For $k_x>>0.0$  (a.u) the curves merged to each other. From Figure 2, we may conclude that in the presence of magnetic field, the Landau sub-bands are formed and at $k_x=0,$  the band-edge of semiconductor moves vertical upward, indicating the increase of band-gap value with the magnetic field. The increase of band-gap value is further enhanced by the electric field, when both electric and parallel magnetic fields are simultaneously present.

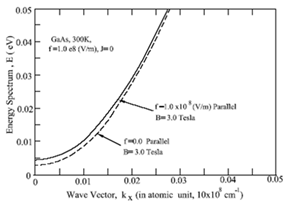
Figure 2 Plots of Energy-Spectrum, E (in eV) against $k_x$  (x-component of wave vector in atomic unit, ${10}^{8}c{m}^{-}$ ¹) for n-GaAs at 300K for B=3.0 Tesla (dotted curve), $f=1.0\times {10}^{8}Vc{m}^{-1}$ and B= 3.0Tesla (solid line).

Figure 3 has been plotted for the density-of-states (DOS), N (E, F), (normalized by $1.6\times {10}^{20}c{m}^{-3}/eV,$ against electron energy E (in eV) under various values of electric field, $\text{f}\left(Vc{m}^{-1}\right).$ We may infer from this that, for $\text{f}=0.0Vc{m}^{-1},$ the curve (solid line) passes through the origin. For finite values of the electric energy (E) axis; besides the curves of (N (E, F) are flattened with respect to f=0.0 Vcm^-1 case. It is to be noticed that, we cannot apply the electric field F (= e.f) to an arbitrary values, the maximum possible value of ${\text{f}}_{max}$  must be limited by: $\text{f}\le {\text{f}}_{max}=\left(\text{E}g{/}_{e.d}\right){\text{Vcm}}^{\text{-1}}$  where ${\text{E}}_g$ is the band-gap of semiconductor (in eV), “e” is the electron charge and “d” is the lattice constant of semiconductor. This is because for the electric field $\text{f}>{\text{ f}}_{max},$ there is a possibility of lattice break-down to happen. So, we must limit the value of electric field strength $\text{f}>{\text{ f}}_{max}.$  Referring to Figure 4 plots are made for n-GaAs at 300K for the following cases:

1. N (E, F, B) (DOS, normalized by 1.6 ×10¹⁸ cm^-3/eV) vs electron energy, E (eV), in presence of f=0.0 (V cm^-1) and a parallel magnetic field, B=3.0 Tesla.
2. For N (E, F, B) vs electron energy, E (eV), in presence of f=1.6×10⁶cm^-3/eV and a parallel magnetic field, B=3.0 esla.
3. From Figure 4, following remarks might be noticed: (a) in both the graphs (1) and (2), the natures of variations of DOS functions with the electron energy (E) are similar with showings singularities. (b) the positions of the singularity points, (Dotted curves, for the case to when F B are present) are shifted to a higher electron energy E(eV) than case when only magnetic field ‘B’ is present marked by solid lines. Since, we conclude from these graphs that in the study of magneto-resistance, the phase value with F B are higher than the case when only magnetic field (B) is present.

Figure 3 Plots for density-of-state function, N (E, F) (normalized by a factor $1.6\times {10}^{20}\left(c{m}^{-1}/eV\right)$ against electron energy, E (in eV) for n-GaAs under various electric fields, f.

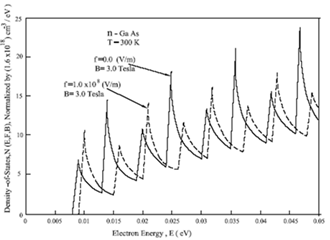
Figure 4 Plots of density-of-states function, N (E, F, B) against electron energy, E (in eV) for n-GaAs at 300K for $f=0.0(v{m}^{-1}$ ) and B=3.0 Tesla (solid curves) and $f=1.0\times {10}^{8}v{m}^{-1}$ and B=3.0 Tesla (dotted curves).

Referring to Figure 5, it appears that DOS function, N(E,F) varies with more or less constant values against electric field (up to a certain value), for different values of Electron energy, E. Thereafter, the rates of fall of N (E, F) value (in magnitude) increases with electron energy (E). Finally, the value of N (E, F) approaches to zero, implying thereby that the carriers disappear near the conduction band (CB) edge, as the applied electric field increase.³ Similar types of vanishing of the carriers have been observed in (CB) experimentally by Miyazawa and Ikoma.¹⁴ In Figure 6, we have plotted DOS function, N (E, F, B) [normalized by a factor of 1.6×10¹⁸(cm³/eV), against electric field, f(Vcm^-1), for electron energy, E=30meV and a parallel magnetic field, B=3.0 Tesla for n-GaAs at 300K. It is shown in Figure 6, that the DOS function is almost a constant value over a certain values of the variation of the electric field. Therefore, as the electric field f is further increased the values of DOS decreases with oscillations and finally approaches to zero value. This implies that in the presence of an electric field and parallel magnetic fields, the availability of the carriers disappear from the CB edge with oscillations due to magnetic field. This phenomenon is unlikely to the cases; only when electric field is present and absence of magnetic fields (Figure 5).

Figure 5 Plots of density-of-State function, N (E, F) (normalized by a factor, $1.6\times {10}^{20}(c{m}^{-3}/eV$ ) for n-GaAs against electric field f (in Vcm^-1) for E=1.0(meV), 10.0 meV) and 50(meV).

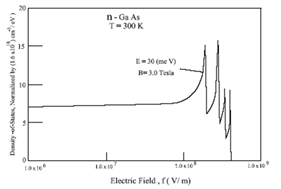
Figure 6 Plots of density-of-State function, N (E, F, B) (normalized by a factor, $1.6\times {10}^{18}(c{m}^{-3}/eV$ ) for n-GaAs against electric field f (in vcm^-1) for E=30(meV), B=3.0 Tesla.

The numerical results presented in the manuscript, would be different for various semiconductor, but the nature of variations, presented here, would be un-altered. The theoretical results, displayed in the paper, would be useful in analyzing various other experimental data related to the above described phenomena. In this context, it might be notice that from the $E-\overline{k}$ dispersion relation, we can formulate the DOS functions but the density-of- states techniques, as used in literature¹⁴ cannot provide the derivations of $E-\overline{k}$  dispersion relation. Therefore, we may conclude that our studies presented here, are more fundamental than those of the existing literatures. This is because the Boltzmann transport equations, which determine the study of the charge, transport properties of semiconductor devices, can be solved if and only if the $E-\overline{k}$  dispersions are known.

Authors are grateful to IACS for providing the library and computer facilities.

None.

The author declares there is no conflict of interest.

1. PK Chakraborty, BN Mondal, BK Choudhuri. Laser-induced modulation of optical band-gap parametersin the III–V-type semiconductors from the density-of-state (DOS) calculations. Pramana J Phys. 2019;92:85.
2. PT Landsberg. Solid-state analogue of the relativistic gases. Phys Rev. 1986;33B:8321.
3. PK Chakraborty, S Choudhury, KP Ghatak. Simple theoretical analysis of the density-of-states function of Kane type semiconductors in the presence of an external electric field. Physica B. 2007;387(1–2):333–343.
4. PN Argyres. Theory of Tunneling and its Dependence on a Longitudinal Magnetic Field. Phys Rev. 1962;126:1386.
5. LI Schiff. Quantum Mechanics. McGraw Hill, 1968.
6. EO Kane. Zener tunneling in semiconductors. J Phys Chem Solids. 1959;12(2):181–188.
7. W Franz Z. Einfluß eines elektrischen Feldes auf eine optische Absorption skante. Natureforch. 1958;13:484.
8. VS Bagaev, NV Zamkovets, LV Keldysh, et al. Kinetics of exciton condensation in germanium. Sov Phys JETP. 1958;7(4):783.
9. HD Rees. Representation of the Franz-Keldysh effect by spectral broadening: Experimental test for GaAs. Solid St Comm. 1967;5(5):365–368.
10. BT Frech. Positronium Diffusion in Solids. Phys Rev. 1968;174:193–991.
11. PK Chakraborty, KP Ghatak. A Simple Theoretical Analysis of the Effective Electron Mass in Heavily Doped III–V Semiconductors in the Presence of Band-Tails. J Appl Phys. 2001;89:1375.
12. BR Nag. Electron Transport in Compound Semiconductor. Springer Series in Solid State Sci. 1980. p. 11–74.
13. H Miyazawa, H Ikoma. Evidence for absence of electrons from conduction band in N-InSb at low temperatures. Solid St Comm. 1967;5(4):229–231.
14. JH Davis. Physics of Low Dimensional Semiconductors. Cambridge University Press, London. 1998. p. 1–458.