The main particularities of the vortexial model of particles resulted in a cold genesis theory of the author (CGT) are compared by those corresponding to the Standard Model of particles. It is argued that the interaction mechanism by intermediary Z–boson and respective– by ‘color’ charges and gluons, considered by the Standard Model for the weak and the strong and nuclear interactions, is semi–formal, a more natural explanation for these interactions being given in CGT by a multi–vortexial model of proton– resulted in CGT as non– destructive collapsed clusters of paired quasi electrons ($e^{*-}{e}^{*+}$ ) and by its resulted vortexial field, which imply also a specific “bag” model of inter–quarks interaction, a “dynamide” model of neutron, with degenerate negatron rotated around the protonic center and a preonic model of quark, with quasi–crystalline kernel formed by kerneloids of –preons of 34 . A vortexial potential with repulsive kernel of ‘sombrero’ type can be proposed as general genesic potential, which can explain also the cold genesis by chiral quantum fluctuations.

Keywords: elementary particle, vortexial field, cold genesis, standard model, sombrero potential

In the quantum mechanics, if ${\psi }_j$  is the complete set of eigen functions of the Hamiltonian, determined by the potential and boundary conditions, the field operator can be defined as $\psi =\sum c_j\times {\psi }_j$ , where $c_j$ are destruction operators and ${\psi }_j$ are field modes or eigen functions of the Hamiltonian. If $|n{\rangle }_j$ is the state of n particles in mode ${\psi }_j$ , the single–particle state is reduced to its wave function ${\psi }_j:|1{\rangle }_j={\psi }_j$   Operating on a one–particle state with a destruction operator, we obtain the vacuum: $c_i.1{\rangle }_i=|0\rangle .$ Operating on the vacuum with a creation operator: $c_i{}^{†}|0{\rangle }_j=|1\rangle$ results in a particle in mode $j$ , i.e.–if the single–particle state $|a\rangle$  {\displaystyle |\alpha \rangle } is empty, the creation operator $c_j{}^{†}$ will fill the state with a fermion. The eigen function ${\psi }_j$  for this particle, is obtained from the field operator $\Psi :{\langle 0\left|\Psi \right|1\rangle }_i=y_i$

The second quantization approach exposes the fact that there is zero–point energy for every field mode y_j, by writing a symmetric Hamiltonian in terms of field operators : $H={\sum }_i{E}_i(c_i.c_i{}^{†}+\mathrm{½}),$  where $E_i$ is the eigen value of the eigen function ${\Psi }_j$  , the second term showing that even in the absence of particles there is an energy $\mathrm{½}{E}_i$ associate with every field mode ${\psi }_j$ , forming the ‘zero point’ energy of the vacuum, confirmed by effects as the Casimir’s effect, the Lamb’s shift and the spontaneous emission, which consists also of intrinsic energies $m{c}^2$ of virtual particles that have a brief existence, called ‘vacuum fluctuations’, which may be related also to the so–called ‘cosmological constant’, used in cosmology.¹

It is known that in the quantum vacuum, at specific energies of excitation, particle–like states can be generated as chiral (spinorial) excitations, individually or in pairs. It was argued also that the vortices play a crucial role in the confinement process, and that condensation of such vortices may be the long–sought confinement mechanism: in the confinement phase vortices percolate and fill the space time volume, in the de confinement phase they are much suppressed.² Also it has been shown that the string tension vanished upon removal of center vortices from the simulations.³

In a Cold genesis theory of the author, (CGT^4–6), it is argued the vortexial nature of the particles’ intrinsic energy $E=m_p{c}^2$ , which– in the electron’s case, results as bosonic condensate of ‘cold’ photons, with a super dense centroid $m_0$ with the radius of $~{10}^{-18}m–$ for the electron, which sustain a stable etherono–quantonic vortex: ${\Gamma }_{\mu }\left(r\right)=2\pi r_{\mu }c={\Gamma }_{\mu }(r_{\mu })+{\Gamma }_B(r>r_{\mu }),$ of ‚heavy’ etherons (m_s» 10^–60 kg)– generating the magnetic potential A and of quantons $(m_h=h\times 1/c^2=7.37x{10}^{-51}kg)-$  generating the particle’s magnetic moment ${\mu }_p$ and vortex–tubes ${\xi }_B$ that ‘materializes’ the B–field lines of the magnetic induction, but also the particle’s spin $S=\mathrm{½}ħ$ given by a spinorial mass $m_{\mu }\approx m_p$ of light photons vortexed with the light’ speed in the volume of Compton radius $r_l=ħ/m_{p}c=r_m,$ which do not contribute to the electron’s mass $m_e$ – which results in CGT from confining ‘cold’ photons with rest mass $m_f{}^0$ –half of their relativist mass $(m_f{}^0=\mathrm{½}{m}_f=\mathrm{½}hn/c^2)$ ,⁶ as saturation value given by the relations:$m_e{c}^2\approx \mathrm{½}{\displaystyle \int {\epsilon }_0}{E}^{2}dV\left(r\right)\approx \mathrm{½}{\displaystyle \int {\mu }_0}{H}^{2}dV\left(r\right)=e^2/8.{\epsilon }_{0}a;$  

$E=c.B=c{\mu }_{0}H;$  $(r<r_m=r_{\lambda }; a=1.41fm)$   (1)

$s=\mathrm{½}ħ=\mathrm{½}{m}_{m}c.r_l\approx \pi \mathrm{½}{m}_{e}c.r_l;$  $r_{\lambda }=ħ/m_{e}c$   (2)

which show that without ${\Gamma }_{\mu }$  –vortex, the m_e–particle cannot be created. It may be argued that this model of electron is compatible with the interpretation given by Giovanni S., Erasmo R. and co–workers^7,8 to the Bohm’squantum potential⁹: $Q=\left({ħ}^2/2m\right)(\Delta \sqrt{\rho }/\sqrt{\rho })$ identified with the kinetic energy of the internal motion ("zitterbewegung") associated with the spin $S$ of a spin $-\mathrm{½}$  particle,$(\rho =R^2=\psi {\psi }^{*};$ $\psi =R.e^{-iS/ħ}$ ; $S=m_{\mu }c.x;x\perp r)$ , in accordance with the Schrodinger’s equation, written in the form:              

$\text{-}{\frac{\text{2s}}{m}}^{\text{2}}\Delta \Psi =E\Psi ;\Psi =\text{R}\cdot {\text{e}}^{\text{-S/}\hslash }\text{ ; s }=\frac{\hslash }{\text{2}}$   (3)

The CGT’s generalization of the relations (1), (2) for the case of the vector photons^4–6 is in accordance with the Esposito’s generalization of the Giovanni’s interpretation of the Bohm’s potential from matter particles to gauge particles, in particular– to photons.¹⁰

The attractive interaction potential $V_{\Gamma }$ given by the vortexial field of superposed vortexes: $\Gamma =\Sigma ({\Gamma }_{\mu }\left(r\right)$ results in CGT by the quantum dynamic pressure $P_d=\mathrm{½}{\rho }_c{c}^2$ , in an eulerian expression:

$V_{\Gamma }\left(r\right)=-u_k{P}_d= -\mathrm{½}{u}_k{\rho }_c{c}^2$   (4)

in which: ${\rho }_c$ –the density of vortexed quanta, given by a single vortex– for the vector photon and for electron and by superposed vortexes ${\Gamma }_m{}^{*}$ of quasi electrons (degenerate electrons with degenerate mass $m_e{}^{*}\approx 0.81m_e$ , charge $e^{*}={\pm }^2{/}_{3}e$ and magnetic moment ${\mu }^{*})-$  for particles heavier than the electron, $u_k$ being the impenetrable quantum volume of the attracted particle, named ‘kerneloid’ in CGT.¹¹

The equation (4) results from the Euler equation: $\omega ={\rho }_f{}^{-1}.P_s (\omega -$ the thermodynamic work per unit mass; ${\rho }_f-$  the fluid’s density; $P_s$ –the static pressure of the fluid) by the Bernoulli’s law considered in the simplest form:

$P_s\left(r\right)+P_d\left(r\right)=P_d{}^0\left(r;v=c\right)=\mathrm{½}{\rho }_c{}^0\left(r\right)c^2=ct.$ ,  (5)

$\nabla V_{\Gamma }=\nabla (w.{\rho }_f.u_k)=\nabla L_f=\nabla (u_k.P_s)=u_k\times \nabla P_s;$  $\nabla P_{s } =-\nabla P_d; \Rightarrow V_{\Gamma }= -u_k.P_d=-\mathrm{½}{u}_k{\rho }_f{v}^2$   (6)

Conform to the “bag” model specific to CGT, even if $P_s{}^0\left(r;v=0\right)$ have different values for different radial distances $r$  , the Bernoulli equation (5) is applicable for each vortex–line $l_{\Gamma }=2\pi r$ and for two diametrally opposed points :$x_1=r_i,$ $x_2=-r_i$ , positioned to the surface of the impenetrable quantum volume $u_{k1}$ of the attracted particle $m_1$ , the supplementary dynamic quantum pressure: $\delta P_{d1}(d-r_i)=\mathrm{½}{v}^2{\rho }_f(d-r_i)$ , respective: $\delta P_{d2}(d+r_i)=\mathrm{½}{v}^2{\rho }_f(d+r_i)$ , introduced in the points $x_1$ and $x_2$ by the vortexial field of an attracting particle $m_2$ positioned at the distance ‘$d$ ’ from the center of $m_1$ will determine– according to eqn. (5), a pressure difference:     

$\Delta P_s\left(x_1{x}_2\right)=-\Delta P_d\left(x_1{x}_2\right)=-(\delta P_{d1}-\delta P_{d2})$ , 

which will generate a force:

$F_{1,2}\approx \pi .r_i{}^2\Delta P_s\left(x_1{x}_2\right)=-\pi \times r_i{}^2\Delta P_d\left(x_1{x}_2\right),$

so– an attractive force toward $m_1$ .

Similarly, the particle m₁ will generate an attractive force $F_{2,1}$ toward the particle $m_2$ . Conform to the model, at equilibrium, for a free m–particle, we have: $P_{si}{}^0\left(r_i\right)=P_{di}{}^0\left(r_i\right)\approx \mathrm{½}{\rho }_p\left(r_i\right)v^2$ ,¹²

$({\rho }_p\left(r_i\right)-$ the local particle’s density), with $v=c$ `.

Conform to eqns. (1)+(4), the inertial mass of a lepton like the electron is formed around a material center of a quantum (etherono–quantonic) vortex ${\Gamma }_{\mu }$  only by attraction of lighter leptons (photons) with non–null volume, i.e–with inertial mass, the ${\Gamma }_{\mu }$  –vortex without the mass of attracted leptons being the classic equivalent of a so–named ‘virtual particle’.

In CGT is possible also to deduce a quark model of cold formed particles with effective (constituent) mass of quarks, which gives the particle’s mass by the sum rule, considering as fundamental stable sub–constituent the basic preon $z^0=42m_e{}^{*}\cong 34m_e$ ,$(m_e{}^{*}\cong 0.81m_e$ – the mass of quasi electrons),  which can form derived “zerons”, (preonic neutral bosons:$z_1\left(3z^0\right)$ ;$z_2\left(4z^0\right)$ ;$z_m\left(6z^0\right)$ , etc.) and two preonic bosons:$z_2\left(4z^0\right)=136m_e$ ;$z_{\pi }\left(7z^0\right)=238m_e$ , which form the light and semi–light quarks $\left(m_q{c}^2<1GeV\right)$ .

According to the model, the quasi–crystalline structure of the preonic kernel of the quark is given by electronic centroids and ‘naked’ heavy photons (corresponding to X–rays and g–rays– which can be emitted at nucleon’s vibration) and can explain the values of the masses of cold formed quarks, mesons and baryons by a quasi–crystalline model of quark, with its current mass with quasi–crystalline arrangement of preonic kernels and with the electronic centroids inter–distanced by a small repulsive field generated by internal photons’ destruction by zero–point vibrations of the electronic centroids.

The particle’s mass results in the approximation of the sum rule, as consequence of the quantum fields’ superposition principle applied to the particle’s cold forming as sum of degenerate electrons, whose total vortexial field ${\Gamma }_v$ can explain also the nuclear force.¹²

–The particles cold forming by clusterizing may result– according to CGT, in a “step–by–step” process¹³ consisting in:

–quark pre–cluster forming, as quasi–crystalline Bose–Einstein condensate of gammons or of preons, at $E_k=\mathrm{½}{m}_{\gamma }{v}^2\to {\mu }_c$ , ($E_k$ the kinetic energy, ${\mu }_c$ –the chemical attractive potential);

– quark (cluster) forming, as non–destructive collapsed quark pre–cluster; (at $E_k=\mathrm{½}{m}_{\gamma }{v}^2\le {\mu }_c$ ) and:

– elementary particle/dark boson forming as confined cluster of quarks with the current mass in the same baryonic impenetrable quantum volume and completed with a shell of ‘naked’ photons; a small impenetrable volume of quasi electrons /preons and a repulsive field of zeroth vibrations impede the destructive collapse. The known possibility to produce bosons and quarks ( $(q-q)$ pairs) by high energy $\left(e^{-}-e^{+}\right)$ interactions sustains the model.

Related to a real process of leptonic particle creation

The creation operator: $c_j{}^{†}$ used in Q.M. can have a classic equivalent, dependent to the impulse density of the ${\Gamma }_{\mu }$  –vortex’s quanta: $c_j{}^{†}~p_f\left(a\right)=={\rho }_f\left(a\right)c$ , which– reported to a reference value, specific to the electron, for example, $({\psi }_j={\psi }^e)$ , gives a creation operator,

$c_j{}^{†}=\sqrt{\left(1+k_j\right)}=0÷\sqrt{2},$

 ($k_j$ –creation/destruction factor):  

$c_j{}^{†}=\sqrt{\left(1+k_j\right)}$ ; $k_j=[{\rho }_f\left(a\right)/{\rho }_f{}^e\left(a\right)]$  ;${\psi }_j=|k{\rangle }_j=c_j{}^{†}.{\psi }^e$  , $(-1\le k_j\le 1;c_j{}^{†}=0÷\sqrt{2};a=1.41fm$   (7)

Because in eqn (1) , we have:

${\epsilon }_0{E}^2\left(a\right)={\mu }_0{H}^2={\rho }_f{}^e\left(a\right)c^2={\rho }_e\left(a\right)c^2$ , it results that:

$k_j=[{\rho }_f\left(a\right)/{\rho }_f{}^e\left(a\right)\left]=\right[{\rho }_c{}^l\left(a\right)/{\rho }_e\left(a\right)],$ the density ${\rho }_f\left(a\right)$ of the H–field’s quanta being equal with the particle’s surface density ${\rho }_c{}^l\left(a\right)$ , conform to CGT,³ $({\rho }_e{}^0\left(a\right)$ being the density in the electron’s surface).

In this case, the values: $0<k_j<1$ corresponds to photons creation, $k_j=0$ – to non–creation, $({\Gamma }_{\mu }=0)$ , and $k_j=-(0÷1)$ corresponds to partial or total destruction of an electron, obtainable by its ${\Gamma }_{\mu }$ –vortex destruction, according to eqn. (1) and to the B–field’s expression resulted in CGT ⁶:  $B\left(r\right)=K_1{\rho }_f\left(r\right).(r_{\mu }c/r)$ , for example– by the electron’s intense vibration, (which determines also its centroid’s vibration,⁶).

If in the relation (3) we take: $S=S_{\rho }=dm.c.x$ , with $\delta m=u_k{\rho }_c$ , and: $S_r={\int }_{\Gamma }\delta m.c.dx=2p\delta m.c.r$  ,

at quantum equilibrium, when:

$e/k_B=k\times S_h/ħ =r/\eta$ ,

$(S_h = 2\pi m_h.c\times r; m_h=h.1/c^2)$ , we can take:

$R=e^{-}{}^{e/2k}=e^{-r/2}{}^h$  (e(r)-the internal entropy) and– in a determinist expression, we will have: ⁶       

$R^2=|\Psi {|}^2={\rho }_c\left(r\right)/{\rho }_0=e^{-r/}{}^{\eta },$  (8)

$({\rho }_c={\rho }_c\left(r\right);{\rho }_0={\rho }_c\left(0\right)).$

For example, supposing that close to the super dense centroid $m_0{}^1$ of an electron was placed another centroid $m_0{}^2\le m_0{}^1$ , with a vortex ${\Gamma }_{\mu }$ ^’ around it, a new leptonic mass $m_l\le m_e$ will be formed, according to eqns. (1), (4), with an associated wave function: ${\Psi }_l=R_l.e^{-iS/ћ}$ , with:

$R_l{}^2=|{\psi }_l{|}^2={\rho }_c{}^l\left(r\right)/{\rho }^l{}_0= k_j.R_e{}^2$ ,

the electron being ‘supplemented’, the amplitude of the associated wave function , being

given by:

$R_s{}^2\left(a\right)={\left(c_j{}^{†}\right)}^2.R_e{}^2\left(a\right)$ , $(R_s{}^2=|{\psi }_s{|}^2={\rho }_s\left(r\right)/{\rho }^e{}_0=e^{-r/\eta })$ ,⁶ $R_e{}^2=|{\psi }_e{|}^2$  ; ${\left(c_j{}^{†}\right)}^2=1+{[({\rho }_c)/({\rho }_f{}^e)]}_a$  (9)

For the same expression of the action: $S=p\left(r\right)x$ , $(x\perp r)$ , we have ${\psi }_s=R_s.e^{-iS/ћ}$ and (7), (8) + (9) gives:

$R_s{}^2\left(a\right)={(R_e{}^2+k_j.R_e{}^2)}_a={\rho }_e\left(a\right)/{\rho }^e{}_0+({\rho }_c{}^l\left(a\right)/{\rho }_e\left(a\right))({\rho }_e\left(a\right)/{\rho }^e{}_0)\approx {\left(R_e{}^2+R_l{}^2\right)}_a$ ;$R_l{}^2\left(a\right)\approx {\rho }_c{}^l\left(a\right)/{\rho }^e{}_{0 }$   (10)

If ${({\rho }^l)}_a={({\rho }_f{}^e)}_a={({\rho }_e)}_a$ ,$\Rightarrow k_j=1$ and the initial electron is duplicated. If $k_j\to -1$ ,then:

$R_s{}^2={(c_j{}^{†})}^2.R_e{}^2\to 0,$ , so the electron is partially or totally destroyed: ${\rho }_c{}^l\left(a\right)/{\rho }^e{}_{0 }=-\delta {\rho }_e\left(a\right)/{\rho }^e{}_0$ , ${(\delta {\rho }_e)}_a\le {\rho }_e\left(a\right)$

${(\delta {\rho }_e)}_a\le {\rho }_e\left(a\right)$  being a loosed density.

The expression (7) of the creation operator $c_j{}^{†}$ is different from those used by QM because while in QM the $c_j{}^{†}-$ operator adds a fermion to the system, the form (7) of CGT increases or decreases the density and the mass of a fermion. It is observed a similitude with the expression of the quantum expectation value used by D. Böhminconcordance with the Q.M.:

$\langle A\rangle ={\sum }_i|c_i{|}^2{a}_i; (\Psi ={\sum }_i{c}_i{\varphi }_i)$  (10’)

in which: $A-$ the observable (the density- in our case),$a_i;{\varphi }_i$ –the eigen values and eigenvectors of A; $(a_i={\rho }_e\left(r\right)-$ in the analyzed case). For a $N^p$ - cluster of (quasi) electrons (as those considered in CGT for the mesons and baryons) affected by the creation operator $c_i$ , the expectation value of its density at distance r from its center will have then the expression:

$\langle \rho \left(r\right)\rangle ={\sum }_i{(c_j{}^{†})}^2{\rho }_i\left(r\right)$ ,  (10’’)

The $c_j{}^{†}-$ operator explaining in this case, in CGT, the fact that the mass of the protonic quasi electron $(m_e{}^{*}\approx 0.81m_e{}^{12})$ is lower than the mass of the free electron, $(k_j<0;c_j{}^{†}<1)$  Similarly it is explained the $\gamma$ -quanta spectrum of vibrated nucleons of a specific nucleus, (photons losing by the ${\Gamma }_{\mu }$  -vortex’ disturbing and the decreasing of ${\rho }_f\left(a\right)$ ).

Related to the total interaction potential

Resulted by attraction in a total vortexial field, the expression (4) of the vortexial potential becomes:

$V_{\Gamma }\left(r\right)=-u_k{P}_d= -\mathrm{½}{u}_k{\rho }_c{c}^2=-V_o.|\psi {|}^2 =-V_o.e^{-r/}{}^{\eta }$ with:$V_o=\mathrm{½}{u}_k{\rho }_0{c}^2$   (11)

However, because the non–null value of the kerneloid’s volume u_k and the ‘zeroth’ vibrations of the particle’s centroid $m_0$ , we must take into account and a small repulsive potential, which– for the interaction between two electrons at distances $r<{\eta }_e\approx 0.96fm$ ,  has the expression: ¹³

$V_r\left(r\right)=2\pi d_i{}^3{\rho }_e{}^o{c}^2{e}^{-r/}{}^{\eta }$   (12)

with: ${\rho }_e{}^o={\rho }_e\left(0\right)=2.22x{10}^{12}kg/m^3$ ^4–6 and $d_i\approx 2x{10}^{-2}fm$ – the equilibrium inter–distance between the attractive magnetic–like force and the repulsive force: $F_r=-\nabla V_r\left(r\right)$ at ordinary temperature of the kinetized particles $(T\approx {20}^{0}C)$ .

For the total potential between two vectorial photons, by similitude with the electron’s case, it may be taken a similar attractive and repulsive potential. But the form (11) of the attractive vortexial potential allow also a semi–formal expression of the total potential between two electrons or two vectorial photons or between a pseudo–scalar and a vectorial photon, in the form of sombrero potential,¹⁴

i.e: $V_{1,2}\left(r\right)=-K_1.|\psi {|}^2 +K_2.|\psi {|}^4$   with: $K_1=V_0= \mathrm{½}{u}_k{\rho }_0{c}^2$ ; $|\psi {|}^2={\rho }_c\left(r\right)/{\rho }_0=e^{-r/}{}^{\eta }$   (13)

The equilibrated (stable) system results for $V_{1,2}\left(r\right)=0$ , i.e for: $|\psi {|}^2{}_e=K_1/K_2$ .

If –for the system of two electrons with anti parallel magnetic moments, we have as in CGT:$d_i\approx 2x{10}^{-2}fm$ and ${\eta }_e\approx 0.96fm$ , it results that: $|\Psi {|}^2{}_e=K_1/K_2=0.9794$ , $\Rightarrow K_2=K_1/|\Psi {|}^2{}_e=1.021\times V_0$  , the eqn. (13) becoming:

$V_{1,2}\left(r\right)=-V_0\times |\Psi {|}^2(1-k_r.|\Psi {|}^2)$ with: $K_1=V_0= \mathrm{½}{\upsilon }_k{\rho }_0{c}^2$ ;$k_r=K_2/K_1=1.021$ ; $|\Psi {|}^2={\rho }_c\left(r\right)/{\rho }_0=e^{-r/}{}^{\eta }$ (14)

It is observed that for $r>d_i\left(V_{1,2}=0\right)$ , the potential $V_{1,2}\left(r\right)$ is attractive. The relation (14) even it is semiformal, it may explain the cold genesis of heavier photons from light photons resulted from chiral fluctuations of quantum vacuum (as etherono–quantonic vortexes in the flowing of the primordial dark energy) by forming of super dense centroids from confined quantons.¹⁵ The quanta density and the intensity of the stabilized etherono–quantonic vortexdepends on the size of the formed centroids m₀ considered in CGT with a possible chiral (spiraled) shape. Because the resulted potential $V_{1,2}\left(r\right)$ not contain any term dependent on the kinetic energy of the particles, (i.e. –on the particles’ temperature, $T_p=\mathrm{⅓}{m}_p{v}^2/k_B)$ , it is understood that the potential (13), (14) is usable for temperature lower than the Bose–Einstein temperature: $T<T_{BE}$ , for the case when the kinetic energy of the particles tends to the value of the chemical attractive potential: $E_k=\mathrm{½}{m}_g{v}^2\to ({\mu }_c)$ , the chemical potential being the total potential of interaction by fields: $({\mu }_c)=V_{1,2}\left(r\right)+V_e\left(r\right)+V_m\left(r\right)$ , and show that even if the electric and the magnetic potentials are of null value $(V_e\left(r\right)=V_m\left(r\right)=0)$ , at $T<<T_{BE}$ the pre–cluster of $B-E$ condensate can collapse until a value of the inter–distance $d_i$ given by: $V_{1,2}\left(r\right)=0$ , i.e. in a non–destructive way, with the cold forming of a bosonic or pseudo–bosonic particle.

It results by eqns. (13) and (14), a relative similitude with the genesic mechanism considered by the Standard model, which use the sombrero potential for describe the spontaneous symmetry breaking and the Nambu–Goldstone bosons,¹⁴ for example, in the form:

$V(\varphi )=-5{\left|\varphi \right|}^2+{\left|\varphi \right|}^4=-25e^{-2}{}^{\theta }(1-e^{-2}{}^{\theta })$  with: $\theta =\sqrt{5}\times e^i{}^{\theta }$  ,$(\theta =(0÷2\pi ))$  .  (15)

which gives an infinity of quantum vacuum excited states.¹⁶

It is observed that the form (14) of the vortexial potential $V_{1,2}\left(r\right)$ is similar to the form (15) specific to the SM, and– by specific values of $V_0({\upsilon }_k{\rho }_0)V_0\approx ({\upsilon }_k;n^k{\rho }_e{}^0)$  and $\eta$ , it may be generalized for the interaction between photons $(k=-1;n\in N)$  or between mesons and baryons with mass $m=n.m_e{}^{*}$  , $(k=+1;n^k\approx 0.9m/m_e{}^{*}$ ).¹²

For example, for the interaction between nucleons, with the values resulted in CGT: $u_n{}^i=0.9f{m}^3$ ; ${\eta }_n=0.8fm$ , a value $V_{\Gamma }{}^n\left(d=2fm\right)=8MeV$ is obtained with $V_0{}^n=115MeV$ (correspondent to the value resulted from the phenomenological model of CGT: $110÷115MeV$ ¹²) if $V_{\Gamma }{}^n\left(0.5fm\right)=0$ ,$\left(k_r=1.868\right)$ .

For the interaction between two nucleonic quarks, considered as in the CGT’s model, with effective mass $m_q\approx \mathrm{⅓}{m}_p$ , i.e–formed by: $n_q=N^p/3=2268/3=756$ quasi electrons (degenerate electrons coupled in gammonic pairs $\left(e^{+}{e}^{-}\right)$ , with mass $m_e{}^{*}=0.8091m_e$ ¹²) the semi–formal potential (14) gives:

$V_0{}^q=\mathrm{½}{\upsilon }_q{}^i{\rho }_e{}^0\left(\mathrm{⅓}0.9m_p/m_e{}^{*}\right)c^2\approx 1.73MeV$ ,

With $u_q{}^i\left(0.21fm\right)=0.03877f{m}^3$  and:

$V_0{}^{q’}\approx 2V_0{}^q=3.45MeV-$ for the vortexial interaction between a couple of two nucleonic quarks and a third nucleonic current quark. With the value: $h=0.8fm$ ¹² and considering that $V^q\left(r_q=0.21fm\right)=0$ , the eqn. (14) gives: $V_0{}^q\left(0.45fm\right)=0.5MeV-$ much less than the value $1.56MeV$ , obtained in CGT for the confining potential of current nucleonic quarks by a specific “bag” model– which explains the quarks’ cluster deconfining at a very high temperature,$T_d=2x{10}^{12}K$ . This result is explained by the fact that the strong force which maintains the current quarks inside the impenetrable nucleonic volume is of “asymptotic freedom” type and is given by a repulsive shell (surface) of a “bag” with the radius $r_b\approx 0.6fm$ ,¹² (as in the Toki & Hosaka bag model).

For a generalization of the eqns. (13), (14) for the potential of $q-q$ interaction, we may propose a generalized potential of “modified sombrero” type, based on the equation (8), in the form:

$V_{1,2}\left(r\right)=-K_1\times |\Psi {|}^2 +K_2\times (\eta /r)\times |\Psi {|}^4$  with: $K_1=V_0= \mathrm{½}{\upsilon }_k{\rho }_0{c}^2$ ; $|\Psi {|}^2={\rho }_c\left(r\right)/{\rho }_0=e^{-r/}{}^{\eta }$   (16)

which– with $V_{1,2}\left(r_e\right)=0$ ,  gives: $K_2=K_1(r_e/\eta )\times e^{re/}{}^{\eta }$ , obtaining the form:

$\begin{array}{l}{\text{ V}}_{\text{1,2}}\text{(r) }={\text{ -V}}_{\text{0}}{\left|\Psi \right|}^{\text{2}}{\text{(1-e}}^{\frac{{\text{r}}_{\text{e}}}{\eta }}\cdot \left(\frac{{\text{r}}_{\text{e}}}{r}\right)\cdot {\left|\Psi \right|}^{\text{2}});{\left|\Psi \right|}^{\text{2}}=R^2=\left(\frac{{\rho }_c(r)}{{\rho }_0}\right)={\text{e}}^{\text{-r/}\eta }\text{; }\\ {\text{ V}}_{\text{0}}=\frac{{\vartheta }_{\text{ki}}}{\text{2}}{\rho }_0{\text{c}}^{\text{2 }}\text{; }\Psi =\text{ R}\cdot {\text{e}}^{\text{-i}\frac{\text{S}}{\hslash }}\text{ ; }{\rho }_{\text{0}}=n^k{\rho }_{\text{0}}^{\text{e}}=\text{0}\text{.9}\frac{\text{m}}{{\text{m}}_{\text{e}}^{\text{*}}}{\rho }_{\text{0}}^{\text{e}}{\text{ ; m}}_{\text{e}}^{\text{*}}\approx \text{ 0}{\text{.81 m}}_{\text{e}}\text{; }{\rho }_{\text{0}}^{\text{e}}=22.24x{10}^{13}kg/m^3\end{array}$   (17)

Which –for the interaction between nucleons (n–n), with $V_{1,2}\left(0.6fm\right)=0$ ; $V_0{}^n=115MeV$ and $\eta =0.8fm$ ,12 gives: $V_{1,2}\left(2fm\right)=-8.93MeV$ , and for the interaction between two quarks $\left(q-q\right)$ , with $V_0{}^q=1.73MeV$ ,$V_{1,2}\left(0.21fm\right)=0$  and $h =0.8fm$  ,12 gives: $V_{1,2}\left(0.45fm\right)\approx -0.645MeV$  and $V_{1,2-3}\left(0.45fm\right)\approx -1.29MeV-$  for the vortexial interaction between a couple of two nucleonic quarks and a third nucleonic current quark– close to the value obtained by the ‘bag’ model specific to CGT, ( $1.56MeV$ ¹²).

The fraction $(\eta /r)$  in the expression of the repulsive potential may be justified by the flux of radially reflected ‘naked’ light photons on the surface of the impenetrable quantum volume ${\upsilon }_i\left(r_i\right)$  of the attractive m–particle, corresponding to a repulsive scalar field. For m $>m_e;u_{kI}=u_i\left(r_i\right)$  we can approximate in eqn. (11) that: $V_{1,2}\left(r_i\right)=0$ , because $u_{kI}$ represents the value of interaction by vortexial field, which have a radius $r_i$ higher than the mechanical radius,$r_i>r_{mi}$ ; for example, for nucleon, $r_i\approx 0.6fm$  and $r_{mi}\approx 0.45$ $fm$  –according to the scattering experiments,¹⁶ the difference $\delta r_i=\left(r_i-r_{mi}\right)$ representing the thickness of a repulsive shell given by brownian ‘naked’ light photons kinetized at the surface of the impenetrable quantum volume $u_{mi}\left(r_{mi}\right)$ , conform to the CGT’s model.¹²

According to CGT, the impenetrable quantum volume ${\upsilon }_{qi}\left(r_q\right)$  of nucleonic quarks which –for concordance with the experiments,¹⁷ is considered with a radius $r_q\approx 0.21fm$ , [6, 12] and of value: ${\upsilon }_{qi}\approx 3.87x{10}^{-2}f{m}^3$ , may be obtained by a semi–empiric equation:¹⁸

${\vartheta }_{ki}={\vartheta }_{ni}\cdot e^{-K\left(1-\frac{m_k}{m_p}\cdot k\right)}\text{; k }=e^{\left(1-\frac{m_k}{m_p}\right)}\text{ ; K }=\text{8}\text{.97; }{\vartheta }_{ni}{\text{(m}}_{\text{p}}\text{) }\approx \text{ 0}{\text{.9fm}}^{\text{3}}{\text{; m}}_{\text{p}}\approx 1836m_e$   (18)

in which the factor ‘$k$ ’ take into account the fact that– inside the quantum volume of a bigger particle, the value ${\upsilon }_{ki}$ of a smaller particle increases proportional with the local density, as in the case of quarks. For (quasi) free $m_k$ particles or with $m_k>m_p$ , we have:$k=1$ .

For electron, it results:$r_i{}^e\approx 3x{10}^{-2}fm$ .

The saturation value of the number of bosons attracted in a volume of fermionic radius around the attractive particle ‘$m$ ’ by its vortexial potential $V_{\Gamma }\left(r\right)$ is given by the eqn. (1). The equilibrium value $r_e$ is proportional with the particle’s temperature: $r_e~T_i$ ,¹³ but for stable baryons, like the proton, the main contribution to the particle’s stability is given by the potential of “asymptotic freedom” type, resulted from the repulsive pseudo–charge of the scalar shell of the particle’s impenetrable quantum volume, $u_i\left(r_i\right)$ , which –at moderate vibration energy of the current quarks, gives a force of quarks retaining: $F_q~-1029N$ , conform to the “bag “ model of quarks confining resulted in CGT.¹²

The previous results show that the eqn. (17), of modified ‘sombrero’ type, may explain the experimentally obtaining of B–E condensate of photons¹⁹ and sustain the conclusion of the cold magnetic (vortexial) confining also of ‘gammons’ or of $z^0$ – preons and of quarks or even of mesons,¹³ with particle–like cold cluster forming by non–destructive collapsing, at $T<<T_{BE}$ , when $E_k=\mathrm{½}{m}_g{v}^2<m_c$ ; (${\mu }_c$ –attractive chemical potential). By comparison, the problem of the particle’s non–collapsing by inter–quarks attraction was solved in the Standard Model by considering an inter–quarks potential of “asymptotic freedom” type, which decreases at quarks’ reciprocal approaching, effect explained in the SM as anti–screening of the quark’s color charge by polarization of virtual gluons in the quantum vacuum.

Related to the particle’s structure
It is known also that the quark model used by the Standard model supposes the existence of an un–structured quark’s kernel of current mass:$2.3÷4.8MeV/c^2$  –for the nucleonic quarks, having a ‘color’ charge of strong interaction, surrounded by a shell of gluons and quark–anti quark pairs having ‘color’ charges of opposite ‘colors’. Even if the gluons are considered in the S.M. with null rest mass, they are the majority contributors to the quark’s effective (constituent) mass by the coupling to the Higgs field which gives them rest mass, according to the Higgs’ mechanism considered in the S.M.

According to CGT,¹³ the quarks of the light and semi–light astro particles (including the baryon $\Omega \left(1627\right)$ ) have similarly a kernel with low mass $(~8MeV/c^2)$ and a photonic shell (of ‘naked’ photons) instead of gluonic one, but it is composed of light quarks ($m_1{}^{+}$ ; $m_2$ , with a mass of $~135m_e$  $137.5m_e$ ;) magnetically attached to a neutral cluster formed by preonic bosons: $z_2\left(4z^0\right)=136m_e$  and $z_{\pi }\left(7z^0\right)=238m_e$ , i.e. – with the kernel formed by preonic kernels (‘kerneloids’, CGT¹¹), of $z^0\left(34m_e\right)$ – preons (pre–quarks)–predicted in CGT in 2005–2006⁴ and experimentally evidenced in 2015 by a team of Hungarian researchers from Debrecen²⁰ but considered as being a quantum of a fifth force, of lepton–to–quark binding.²¹

According to CGT, the electron’s mass is given mainly by the inertial masses of a number of ‘nakes’ photons (virtually reduced to their kernel, i.e. with loosed evanescent part) attracted by the vortexial field of the electron’s magnetic moment, given by an etherono–quantonic vortex:${\Gamma }_{\mu }{}^e={\Gamma }_B{}^e+{\Gamma }_c{}^e$  , given by a vortex of ‘heavy’ etherons ( $~{10}^{-60}kg$ ) which explains specific effects (like the Aharonov–Bohm effect) of the magnetic potential A and by a vortex of ‘quantons’ ($m_h=h.1/c^2=7.37x{10}^{-51}kg$ ), which generates quantum vortex–tubes of the magnetic induction’s field lines ${\xi }_B$ .

In CGT is considered also a small impenetrable quantum volume u_I not only for nucleons and quarks, but also for the electron and for $z^0$ –preon, with a radius: $3x{10}^{-2}fm$ –for the free electron, respective:$3.5x{10}^{-2}fm$  for the $z^0$  –preon– values given by the eqn. (18),¹⁸

Even if these ‘impenetrable’ quantum volumes ${\upsilon }_I$ (“kerneloids”) can be penetrated by photonic or electronic super–dense centroids, (fact evidenced in experiments of X–rays scattering on electrons and electrons scattering on nucleons), they impede the particle’ destroying by quarks/quasielectrons collapsing, with the aid of a small repulsive field of quantum perturbation given of ‘zeroth’ vibrations of the particle’s centroid(s), which is increased at high intrinsic quantum temperatures.

 In concordance with the equation (1) a similar kerneloid may be considered also for the ‘quarcins’ $c_0{}^{\pm }\approx 17m_e$  ($~8.7MeV/c^2$ ) considered in CGT as last sub–components of the quarks.

Also a problem of the SM’s model of quark is the explaining of the repartition of the mass of gluons (and ‘sea quarks’ resulted as virtual ($q\overline{q}$ ) pairs of split gluons) to the valence quarks, at the quark’s/baryon’s transforming.

In CGT, the similar problem, of explaining the retaining and transporting of a mass of “naked” photons of the particle’s quantum volume proportional with the current mass of the quark in strong interaction, is explained by the vortexial field of the quark’s kerneloid, given by the sum of quantum vortexes ${\Gamma }_{\mu }{}^{*}$  of the degenerate magnetic moments of its preonic quasi electrons, in accordance with the superposition principle of the quantum mechanics. Also, a quarcic shell of “naked” photons, i.e.–penetrable by other particles, explains the possibility of elastic interaction between nucleons better than a shell of gluons, considered by the SM and the value of the proton’s radius experimentally determined, ( $0.84÷0.87fm$ ). Because these electronic/quarcinic/preonic kerneloids, by their (quasi)electronic vortex(es) of the magnetic moment(s) ${\Gamma }_{\mu }{}^e$ , attract and retain in their vortexial field a mass of ‘naked’ photons proportional with their mass, i.e– proportional with the number of the contained electronic centroids $m_0$ , in accordance with the eqns. (1) , (4), (17), we may formally consider the mass of these kerneloids as ‘current mass’ of the quarcins/preons/quarks, $m^c$ , which– in addition with the mass of the attracted/retained ‘naked’ photons ($m^f$ ) gives the effective (constituent) mass $m^C$ of the quarcins/preons/quarks, similar to how in the Standard Model, the shell of gluons of the current quark mass gives– by addition, their constituent mass, ( the mass of the quarcins of CGT being to the same size order as the mass of the $u$ , $d$ –quarks of the SM). In these approximation, conform to CGT, the mass of the impenetrable quantum volume of the nucleon or of other baryon or of mesons is given mainly by the mass of the preonic/quarcic kerneloids, the shell of the impenetrable quantum volume of the particle being given by ‘naked’ photons which – for a charged particle, explain also their charge and the electromagnetic (photonic) radiation emitted at the charge’s vibration or deceleration.

 In this case, even if the quarks have a small vibration liberty, $l_v$ , inside the particle’s ‘impenetrable’ quantum volume, their relative stability (higher for the nucleonic quarks) may be explained in CGT, by a quasi–crystalline arrangement of preonic kerneloids, which – at cold formed quarks by clusterizing, is ‘inherited’ from the preonic non–collapsed quasi–crystalline pre–cluster formed by pre–clusters of $z_2$  and $z_{\pi }$ preonic bosons,¹³ the rotation of the cluster of quarcic kerneloid being probable more energic.

In Figure 2 it is observed that the calculated value: $r_z=3.5\times {10}^{-2}fm$ ¹⁸ of the preon’s kerneloid, ensures a mean distance: $d_i\approx \left({}^2{/}_3\right).r_z\approx 2\times {10}^{-2}fm$ between the electronic centroids $m_0$ on the radial direction, the length of the preon resulting of value: $l_z=6\times d_i\approx 0.12fm$ . The previous value: $d_i\approx 2\times {10}^{-2}fm$ , is in concordance with the value of the root–mean square charge radius of the free electron: $r_e=0,0118fm$ , resulted from calculations made by Storti and Desiato,²² and to some high–energy scattering experiments reported by Milonni²³ which gave a value: $r_e=0.01fm$ – which is the electron’s kerneloid mechanical radius, conform to the CGT’s model¹¹ and justfy the approximation $V_{1,2}\left(r_i\right)=0$ used for eqn. (17) in which ${\upsilon }_{kI}={\upsilon }_i\left(r_i\right)$  represents the value of interaction by vortexial field, with r_i obtained by the eqn. (18), ( $r_i{}^e=0.03fm$ –for the electron).

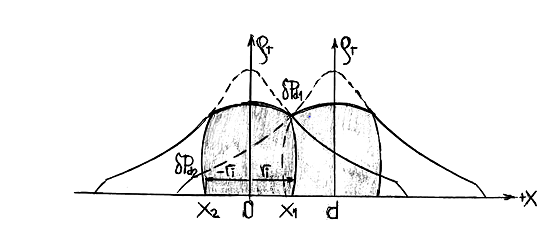
Figure 1 The generating of the attraction force by a vortex field

Figure 2 apreonic z- layer of a quarcic kerneloid

Because the quasi–crystalline structure of ($u$ ,$d$ )– quark kerneloid have three layers– in CGT, ( $m_{1;2}$ ;$z_{\pi }$ ;$z_{\pi }$ –Figure 2) with (4; 7; 7) $z^0$ –preons,¹³ it results an approximate length of the ($u$ ;$d$ )– quark kerneloid: $l_q=3l_z\approx 0.36fm$ , the minimal possible radius resulting of value: $r_q{}^0=3\times r_z=0.105fm$ , value which is the radius of mechanical interaction and which– compared with the resulted radius value of the quark’s current mass: $r_q\approx 0.21fm$ ,¹⁷ of interactions by vortexial field– in CGT, indicates a small vibration liberty $l_v$ of the $z^0$ – preons inside the quark’s kerneloid. The mass of the current quark results approximately as total mass of its preonic kerneloids.

The considered radius of the quarcic kerneloid: $r_q\approx 0.21fm+$  a repulsive shell ${\delta }_q\approx 0.09-0.1fm$ ,¹⁸ is in accordance with the value of $~0.3fm$ obtained by some scattering experiments.¹⁷ The last determined value for the quark’s radius: $~0.43\times {10}^{-18}m$ ,²⁴ corresponds to the radius of the super–dense electronic centroid, conform to CGT,^4–6 being close to the upper limit determined by X–rays scattering on electron.²⁵ Also, the resulted mechanical radius of the nucleonic impenetrable volume, given by three coupled quarcic kerneloids, results of value: $r_i{}^n\approx (2r_q+{\delta }_q)\approx 0.5fm$ –in accordance with the $r_{mi}$ – radius’ value of the mechanical impenetrable kernel ${\upsilon }_{mi}{}^n$ resulted from experiments of electrons scattering to nucleons,  ( $r_{mi}=0.45fm$ ,¹⁶). It results that the proton’s stability results by a strong attractive interaction between quarcic kerneloids and a low vibration liberty– as consequence of the static quantum pressure of ‘naked’ photons upon the surface of the impenetrable quantum volume of the nucleon, which gives a static repulsive shell of radius $r_i{}^{*}=a_i\approx 0.6fm$ , according to a ‘bag’ model of strong interaction resulted in CGT,¹² more probable being the rotation of the cluster of quarcic kerneloid, generated by the magnetic moment’s vortex ${\Gamma }_{\mu }$  , in CGT. Also, because the fact that the magnetic moments of quasi electrons of the $z^0$ –preon are axially coupled on the axial direction, forming a common vortex–tube ${\Gamma }_{\mu }{}^{*}$  , the central, un–paired ${\Gamma }_{\mu }{}^{*}$  –vortex–tube gives the preon’s magnetic moment and similarly– the central un–paired preon gives the magnetic moment of the pseudo–quarcic neutral cluster of preonic bosons which– by an attached un–paired quasi–electron, gives the cold (quasi–crystalline) quark.

At ‘hot’ formed quarks, a similar quasi–crystalline re–arrangement of preonic kerneloids may result by internal re–arrangement of the common preonic cluster of quarks, by transfer (changement) of kerneloids of preonic bosons ( $z^0$ , $z_1\left(3z^0\right)$ ,$z_2\left(4z^0\right)$ , $z_{\mu }\left(6z^0\right)$ , $z_{\pi }\left(7z^0\right)$ ) from a quarcic kerneloid (internal or resulted by interaction with other particles or with bosons of the quantum vacuum) to another cuarcic kerneloid, with the aid of the vortexial attractive field of a kerneloid upon the impenetrable quantum volume of another kerneloid, (similar to the case of the nuclear interaction between nucleons –conform to CGT^4–6).

These bosonic kerneloids are mechanically similar with the gluons considered by the SM, a higher similitude being given by the fact that the resulted composition of the $z^0$ –preon, as aquarcinic pair:$(c_0{}^{+*}{\overline{c}}_0{}^{+*})$ $(~2\times 8.7MeV)$ , is similar to the composition of gluons of the SM considered as pairs $(q\overline{q})$  , of quarks with current mass, with the main difference that in the SM, the nucleonic current quarks haven’t a sub–structure but have a “color” charge. In CGT, even it seems that a sub–structure of the quarcins $c_0{}^{*}$ is not strictly necessary, the considered substructure of quasi electrons may explain the nuclear force as given by scalar attraction in their vortexial field of its magnetic moment generated by each quasi electron. But a semi–formal model of constituent quark with bosonic kerneloids in the quark’s shell (instead of heavy photons– as in CGT) supposes a quasi–crystalline arrangement of these kerneloids, because their magnetic interactions, according to CGT, which would prevent the nucleons’ centers from approaching at a distance of $~0.9fm$ between them.

However, some high energy gamma–quanta, of $1÷100MeV$ , emitted at nuclear de–excitation, as in reaction (1), may be explained in a Galilean relativity as In CGT, as clusters of gammonic kerneloids, particularly– kerneloids of $z^0-,z_k$ – preons,$(k\ge 1)$  , emitted either by the vibrated (excited) quark’s kernel or from the quantum shell of the nucleon’s quantum volume, at the nucleon’s vibration, by the force of dynamic quantum pressure of the ${\Gamma }_{\mu }$  –vortex of the proton’s magnetic moment. Conform to CGT, at their releasing, these clusters re–obtain a photonic shell of mass proportional with the number of quasi electrons’ kerneloids which compose the preonic boson’s kerneloid, i–e– corresponding to boson’s effective mass, by the negentropy of the quantum vacuum given by etherono–quantonic winds (fluxes) which explains also the constancy of the magnetic moment of the free charged particles.^4–6 A similar conclusion, of a quasi–crystalline arrangement of quarcic gluons, results also for the quark model of the SM, because the strong interaction between quarks and gluons, given by the so–named “color” charge of quarks and a resulted interaction potential of “asymptotic freedom” type.

It may be argued also –in CGT, that the –charge is given by an electron also in the case of the proton (whose charge is given by a positron^4–6), the E–field’ quanta (vectorial photons, “vectons”–in CGT) resulting from pseudo scalar quanta of background radiation of $~2.73K$ and having a cylindrical density variation inside the electron (which is generated by the vortexial energy of the electron’s magnetic moment and as consequence of its barrel–like vortexial form), transformed into spherical distribution for $r\ge a$ , as consequence of the spin’s precession movement (Figure 5):

${\rho }_v\left(r\right)= {\rho }_v{}^0\left(r_v{}^0/r\right)$  for $r_v{}^0<r\le a$ ; ${\rho }_v\left(r\right)= {\rho }_e\left(a\right)·{\left(a/r\right)}^{2 }$  for $r>a$ , 

${\rho }_v{}^0={\rho }_e\left(a\right)·\left(a/r_v{}^0\right)={\rho }_e{}^0.e^{-r/}{}^{\eta }\Rightarrow r_v{}^0=0.64fm$   (19)

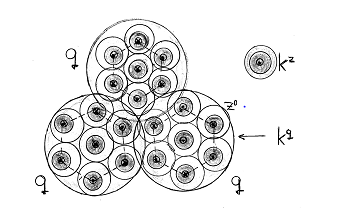
Figure 3 The cold forming of a baryonic kerneloid (CGT)

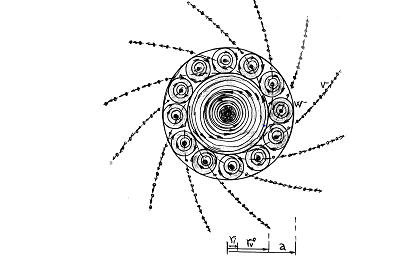
Figure 4 The vortexial electron model (CGT) ; (v- -vecton ; w- -vexon)

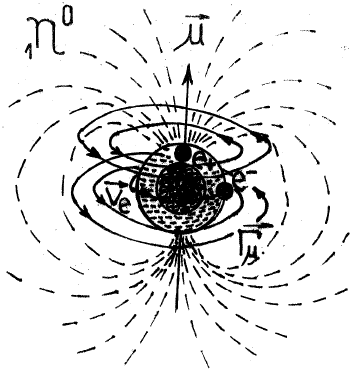
Figure 5 The neutron’ model

The electron’s kerneloid, with a radius of mechanical interactions, resulted of value$r_{\epsilon }=0.01fm$ in CGT [11], ensures the forming of a etherono–quantonic vortex ${\Gamma }_{\mu }$  around it and implicitly– also a vortex of vectons (which can escape from the level of the surface of radius $r_v{}^0=0.6÷0.64fm$ –Figure 5 more dense thanin the case of a vectorial photon as consequence of a bigger superdense centroid m₀ which sustain and stabilize the ${\Gamma }_{\mu }$ –vortex, conform to CGT. Also, the cylindrical density variation inside the electron for $r_v{}^0<r\le a$ , suggests a fusi form centroid, with the length sensible bigger than its diameter , considered with chirality ${\zeta }_0=\pm 1$ (of spiral form) in CGT,⁶ the electron’s charge being given by quantum vortex–tubes with ${\zeta }_w=-{\zeta }_0$ .

If the pairs of electronic centroids with opposed chiralities gives electronic neutrinos of Majorana type and mass $m_v\approx {10}^{2}eV/c^2$ – conform to CGT,^4–6 it is possible that similarly – a quantity of photonic centroids of sensible lower mass, of thermalised photons of the quantum vacuum can form pairs with opposed chiralities which corresponds to a quantity of pseudo–neutrinos of ‘dark matter’ which includes the so–named ‘axions’, with a rest mass of ${10}^{-5}÷{10}^{-3}eV/c^2$ ,²⁶ the electronic superdense centroids resulting in this case from confined pseudo–axions which in turn results from vortexially (magnetically) confined quantons, conform to CGT. The large mass spectrum of these photonic centroids (pseudo–axions) results theoretically from the large spectrum of photons in accordance with the vortexial model of pseudo–scalar photon, composed by two magnetically coupled vectorial photons (“vexons”– in CGT⁶), as in the Munera’s model of photon, but with the diameter $l_w/2$  ($l_w$ –the length of the pseudo–scalar photon)dimensioned like in the Hunter–Wadlinger’s model of photon and considered a vortex of heavy etherons (“sinergons’– in CGT,⁶ $m_s\approx {10}^{-60}kg$ ) around the quanton’ mass, $m_h=h/c^2$ and a density ${\rho }_s\left(r\right)={\rho }_s{}^0.\left(r_w/r\right)$  of Brownian sinergons (but also a sinergonic vortex ${\Gamma }_s$  with a similar variation of its density) around the kerneloid of the vexon’s inertial mass, $m_w\left(r_w\right)$ .

For:$l_w/2\approx {\lambda }_0/\pi$ , the dynamic equilibrium for the vortexed quantons or clusters of quantons inside the Compton radius: $r_{\lambda }={\lambda }_0/2\pi$ , is given by a magneto–gravitic force of Magnus type generated by the sinergonic vortex of the quantons rotated with $v=c$ to the vortex line (circle) $l_r=2\pi r$ by the ${\Gamma }_s$ –vortex in the ${\rho }_s\left(r\right)$ –density of sinergons, in the form:

$F_{sl}=2r_c.{\Gamma }_c\left(r_c\right).{\rho }_s\left(r\right)\times c=4\pi r_c{}^2.c^2.{\rho }_s{}^0.\left(r_w/r\right)=m_h{c}^2/r;r\le r_{\lambda }=h/2\pi mc$   (20)

by the resulted condition: $4\pi r_c{}^2.{\rho }_s{}^0.r_w=m_h=h/c^2$ , with:${\Gamma }_c\left(r_c\right)=2\pi r_c.c;$ $r_c$  − the quanton radius; ${\rho }_s{}^0$ − the density of sinergons at the vexon’s inertial mass surface of radius $r_w\le a$ ; $m_h$ – the quanton’ mass; ${\Gamma }_c\left(r_c\right)$ − the circulation of sinergons at the quanton’s surface. It is observed that –because the generating of a magneto–gravitic (Lorentzian) force of Magnus type by the sinergonic vortex of the quantons and the ${\rho }_s\left(r\right)$ –density of sinergons, the vector photon and the electron seems to be a micro–black hole but not because the gravitational force (which is neglijible in this case). For a heavier particle, formed as non–destructive collapsed cluster of quasi electrons, it results that at very low temperatures, ($T\to 0K$ ,$E_k=\mathrm{½}{m}_{\gamma }{v}^2\to {\mu }_c$ ), the force $F_{sl}$ canensures the maintaining of quantons inside the particle’s volume if the quasi electrons are coupled in pairs with anti parallel magnetic moments– maintained at a diminished (degenerated) value, in accordance with the fields superposition principle. This fact can explain the detection of cosmic ultra–heavy particles (of “oh–my–god” type ]xx]: $m{c}^2\approx {10}^{20}eV$ , $(~5\times {10}^{-16}kg)$  , without the Einsteinian relation of speed–depending mass variation.

There are at least three hypothetically possible situations regarding the action of some bosons (in particular – radiation quanta) on the surface of the nucleonic volume:

1. the pressure on the surface of the nucleonic ‘bag’ is given by Brownian kinetic quanta, (such as molecules);
2. the pressure is given by the quanta of some quantum “winds”;
3. the pressure is also given by Brownian kinetic quanta and quantum winds;

In the first case, a), the explanatory problems that appear regarding the particles consist in the following:

In the case of the photon, the purely Brownian motion of the quanta and sub–quanta of the "quantum vacuum" would prevent the generation of vortices around the super–dense centroids of photons, even and their c–velocity (the speed of light in vacuum), which would make inexplicable the dualistic, wave– particle character of photons, because the electromagnetic wave property involves both electric field vectors E and magnetic field vectors, H– vectors that can be explained only by the quantum–vortex character of the magnetic field lines ${\xi }_H$ (vortex–tubes of etherons and quantons –conform to CGT ^4–6). – In the case of the electron, because the Brownian motion does not generate vortices, by pure Brownian kinetics of the sub–quantum and quantum environment neither the electric charge nor the perpetual magnetic moment of the electron could be explained micro physically;

In the case of nucleons, if the quantum and sub–quantum medium were only brownian, without vortices, and if the quarks would be with a radius of approx. ${10}^{-18}m$ (according to the conclusions of quantum mechanics), to keep the quarks together inside the nucleon, a pressure on them from the outside would be necessary, as in the case of the “bag” model of nucleon with quarks held together by an external pressure. The explanatory problem that arises is that– at a relatively small distance of the nucleonic quarks from each other, (at distances of maximum 1fm), the static quantum pressure generated by the pseudo–Brownian motion of the quanta with which the quantum and sub quantum medium of "zero" point energy, that intervenes in the space between quarks, it would generate a greater rejection between them, increasing the inter–distance between quarks which are eclipsing each other. Or– the experimental data showed that –apparently paradoxical, over short distances, below 1fm, the force of their reciprocal approach increases with the inter–distance ("asymptotic freedom" effect). It results that the hypothesis a) is not in concordance with the experimental observations on the properties of elementary particles.

In the case of the atoms, by pure Brownian kinetics of the sub quantum and quantum medium cannot be explained micro physically neither the magnetic moment of the nucleons and of the nucleus and implicitly– nor the perpetual motion on the orbital of quasi–constant mean radius of the atomic electrons, with angular velocity $\omega =v/r$ – quasi–constant, (in the case of the Bohr atomic model), case in which – according to the laws of the classical electromagnetism, the electrons should gradually lose kinetic energy by radiative emission and eventually fall on the nucleus– fact that does not take place, phenomenon well explained only in the case of the atomic vortex model; according to quantum mechanics, the orbital motion of atomic electrons without radiation emission and without diminution of their kinetic energy is only postulated, not explained.

In the case of nuclear interaction, between two or more nucleons, the standard model of quantum mechanics considers (in the quantum “chromo dynamics" theory) the existence of residual gluons of the nuclear field, for explain the interaction between nucleons, being postulated the existence of a so–called “color charge” of nucleonic/gluonic quarks, (similar to electrical charge but of significantly higher value), but without a plausible explanation for the microphysical nature of this “color charge”.

Also, is not clear in the SM how in the case of a baryon like ${\Lambda }^0$ (1116)– which is considered with the structure ($u$  $d$   $s$ ) and is transformed by a reaction: ${\Lambda }^0\to (p^{+}+{\pi }^{-})$ or: ${\Lambda }^0\to (n^0+{\pi }^0)$ , the losing of a $\pi$ – meson from the s–quark (whose current mass is considered elementary, without structure) take place by the losing of a couple of ($u$ `$d$ )– or ($d$ ` $d$ )– of valence quarks with the same current mass as those of the nucleons but carrying a considerable lower but exact mass of gluons, $~68MeV/c^2$ (per quark, compared to $~310MeV/c^2$ per quark –in the case of the nucleon).

In the hypothetical variant a) or c) we could imagine a model of nuclear interaction similar to the Fatio/LeSage model of gravity: with attractive force given by difference of pressure generated by Brownian quanta or by quantum winds, pressure difference generated by the reciprocal eclipsation of the nucleons in report to the action of the quanta on their surface; but because the nuclear force is about  times stronger than the gravitational force and because the tendency towards equilibrium of the quantum medium, that would homogenize the values ​​of density and pressure of the quanta, to explain the value of nuclear force by static quantum pressure difference generated without vortices would be necessary a considerable quantum density, close to the density of the nucleon, $~{10}^{17}kg/m^3$ ).

Or such a value of the density of the quantum medium corresponding to the "zero" point energy, even if it may be supposed as existent in the planetary and stellary space, it would produce an accentuated red shift effect of the spectrum of light radiation from distant stars by the effect of radiation “aging”, by a considerable drag force at the photons passing through this quantum medium, even if is taken into account also the d’Alembert’s paradoxe [28]– in contradiction with the fact that we can observe through the telescope also the radiation of very distant stars.

It results therefore that the nuclear interaction between nucleons cannot be explained naturally without the concept of ‘quantum vortex’, the use of postulates such as the existence of the "color" charge of quarks being more formal than a natural explanation, (more hypothetical than phenomenological).

The mechanism of the beta decay is explained in the Standard Model by the conclusion that a nucleonic down quark of a neutron is changed into an up quark, converting the neutron into a proton by the emission of an an intermediary carrier: a virtual W^––boson, having a large mass (approximately $90 GeV/c^2$ ) and a short lifetime, of under seconds, which has a very short effective action range (around ${10}^{-17}$  to ${10}^{-16} m$ [29]) and is transformed into an electron and an electronic antineutrino, (which may explain the mass difference between the quarks $d$ and $d$ ). The explanation of the SM for the large energy spectrum of the beta–electron is the conclusion that it share the W^—boson’s transforming energy, , with an electronic antineutrino (or a neutrino– in the ${\beta }^{+}$ – decay). So, the considered $W$ ^—boson, resulted in the electro–weak theory, is essential in the weak interaction’ explaining, for the S.M.