The 1D Fokker-Planck equation (FPE) plays a major role in the propagation of light in the universe. It specifically describes small angle scattering of photons (and electrons) as they travel in participating media. In particular, the differential scattering term representing the phase function scattering law enables the small angle scattering. This term also makes the FPE a challenge to solve in the discrete ordinate sense. Our approach utilizes adding and doubling, which has been successfully applied since the 1960s to solve the linear Boltzmann equation. With the help of Morel’s discrete ordinate equivalence of the angular Laplacian, the FPE becomes similar to the discrete ordinates equation of linear transport theory. We then take advantage of the similarity through adding and doubling for its solution.

The 1D Fokker-Planck equation (FPE) is one of the most consequential equations of particle transport theory. Small angle scattering of electrons and photons played a significant role in the early universe before the combination of protons and electrons to form the hydrogen atom allowing photons to scatter to the greater universe as the Cosmic Microwave Background (CMB) we see today. Here, we present a new method to solve the FPE employing adding and doubling as proposed by van de Hulst.¹ Our approach is in contrast to previously published solutions, such as response matrix,² finite differences³ and eigenfunction expansion⁴ and offers the simplicity of the direct numerical solution of a first order ODE. For its solution we choose adding and doubling, which had proven to be one of the more precise methods of solution of the transport equation.⁵

We begin with the formation of the discrete ordinate approximation to the FPE. The formulation includes the discretization of the angular Laplacian required to preserve the first and second moments of particle intensity. The first order form of the equation naturally leads to a matrix exponential solution for which we employ a Crank Nicolson numerical approximation. By an appropriate choice of exponential approximation, we find the response matrix, which gives the exiting angular intensity in terms of the incoming intensity. Finally, we evaluate the matrix multiplications to give our final numerical benchmark of exiting intensities for angularly uniform incoming intensities to which we compare to the response matrix benchmark of Ref. 2.

The SN equations

The 1D Fokker-Plank equation (FPE) without volume source is

$\left[\mu \frac{\partial }{\partial z}+\alpha \right]\psi \left(z,\mu \right)=\sigma \frac{\partial }{\partial \mu }\left[\left(1-{\mu }^2\right)\frac{\partial \psi \left(z,\mu \right)}{\partial \mu }\right]$   (1a)

The solution is to include half-range boundary conditions

$\begin{array}{l}\psi \left(0,\mu \right)=f\left(\mu \right),\mu \in \left(0,1\right]\\ \psi \left(a,\mu \right)=g\left(\mu \right),\mu \in \left[-1,0\right)\end{array}$   (1b)

at the boundaries x = 0 and a of a slab of width a. The momentum transfer,

$\sigma =\frac{{\sigma }_{tr}}{2}=\left(1-g\right)\frac{{\sigma }_s}{2}$ ,  (1c)

also known as the transport cross section is characteristic of the FPE, where g is the average scattering cosine.

The method of adding and doubling requires discretization of both direction μ and spatial variable z, though spatial discretization has an analytical element to it.    We first consider the directional (or angular) discretization, following from the N zeros of the Legendre Polynomial on the full-range interval [-1,1]

$P_{2N}\left({\mu }_m\right)=0;m=1,\mathrm{....},2N$ .  (2a)

The discretization [also called the Sn (Segment N) approximation], where

$\begin{array}{l}0<{\mu }_m<1,m=1,\mathrm{...},N\\ -1<{\mu }_m=-{\mu }_{2N-m+1}< 0,m=N+1,\mathrm{...},2N\end{array}$   (2b)

forms the basis of the discretized solution. Note that 2N assumes the role of quadrature order in the discrete ordinates solution of the radiative transfer equation and the zero ordinate is necessarily avoided since 2N is even.

Applying the Sn approximation, the exact solution relates to the approximate as

$\psi \left(z,{\mu }_m\right)={\psi }_m\left(z\right)+\epsilon \left(z,{\mu }_m\right)$ .  (3a)

$\epsilon \left(z,{\mu }_m\right)$  is the discretization error, and the Sn balance equation is

$\left[{\mu }_m\frac{\partial }{\partial z}+\alpha \right]{\psi }_m\left(z\right)=\sigma {\nabla }_m^2{\psi }_m\left(z\right).$ .  (3b)

${\nabla }_m^2$  is the discretized FP operator,^4,6

$\frac{\partial }{\partial \mu }{\left[\left(1-{\mu }^2\right)\frac{\partial \psi \left(z,\mu \right)}{\partial \mu }\right]}_{{\mu }_m}\simeq {\nabla }_m^2{\psi }_m\left(z\right),$   (4a)

expressed as²

${\nabla }_m^2{\psi }_m\left(z\right)\equiv \frac{1}{{\omega }_m}\left[\begin{array}{l}{\beta }_{m+1/2}\left({\psi }_{m+1}\left(z\right)-{\psi }_m\left(z\right)\right)-\\ -{\beta }_{m-1/2}\left(\psi m\left(z\right)-{\psi }_{m-1}\left(z\right)\right)\end{array}\right]$   (4b)

with

$\begin{array}{l}{\beta }_{m+1/2}\equiv \frac{{\gamma }_{m+1/2}}{{\mu }_{m+1}-{\mu }_m}\\ {\gamma }_{m+1/2}={\gamma }_{m-1/2}-2{\mu }_m{\omega }_m,{\gamma }_{1/2}\equiv 0.\end{array}$   (4c)

For ${\omega }_m$

$\begin{array}{l}{\omega }_m={\tilde{\omega }}_{N-m+1},m=1,\mathrm{...},N\\ {\omega }_{2N-m+1}=\tilde{\omega }m,m=N+1,\mathrm{...},2N,\end{array}$   (4d)

which is the corresponding Gauss quadrature weight for the prescribed ordinate at m.

If one defines the L matrix as

$L=\left[\begin{array}{cccccccc}-{\nu }_1& {\beta }_{3/2}& 0& 0& \mathrm{...}& \mathrm{...}& & 0\\ \beta 3/2& -{\nu }_2& {\beta }_{5/2}& 0& \mathrm{...}& & & \mathrm{...}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{....}& & & & \\ 0& \mathrm{...}& {\beta }_{m-1/2}& -{\nu }_m& {\beta }_{m+1/2}& 0& \mathrm{...}& 0\\ \mathrm{...}& & \mathrm{...}& \mathrm{...}& \mathrm{...}& & & \\ & & & \mathrm{...}& \mathrm{...}& \mathrm{...}& & \mathrm{...}\\ \mathrm{...}& & & & \mathrm{...}& {\beta }_{2N-3/2}& -{\nu }_{2N-1}& {\beta }_{2N-1/2}\\ 0& \mathrm{...}& & & \mathrm{...}& 0& {\beta }_{2N-1/2}& -{\nu }_{2N}\end{array}\right]$   (5a)

with

${\nu }_m\equiv {\beta }_{m+1/2}+{\beta }_{m-1/2}$ ;  (5b)

then the balance equation, Eq(3b), becomes the following set of first order ODEs:

$\left[M\frac{\partial }{\partial z}+\alpha \right]\psi \left(z\right)=\sigma W^{-1}L\psi \left(z\right)=0$ .  (6a)

with

$\begin{array}{l}W\equiv diag\left\{{\omega }_m\right\}\\ M\equiv diag\left\{{\mu }_{{}_m}\right\}.\end{array}$   (6b)

Equation (6a) is to be resolved numerically within the slab; but for this presentation, we only report the exiting intensity at slab boundaries.

Before continuing, some additional explanation is in order to complete the derivation of the Sn equations. We have chosen the full-range discretization rather than the half- range over [-1,0),(0,1] since there is evidence that full-range gives better precision.² Secondly, there are at least three known discretizations for the angular Laplacian. The one chosen preserves the diffusion limit in that the zeroth and first moments of the intensity are exact for the given quadrature order 2N.

The Response Matrix

A reformulated Eq(6a) is

$\frac{d\psi \left(z\right)}{dz}=M^{-1}\left[\sigma W^{-1}L-\alpha {\rm I}\right]\psi \left(z\right)\equiv A\psi \left(z\right)$   (7a)

with formal solution in spatial cell of thickness h = z_n+1-z_n,

$\psi \left(z_{n+1}\right)=e^{Ah}\psi \left(z_n\right)$ ,  (7b)

since A is independent of z.

To initiate a Crank-Nicolson finite difference approximation, the exponential in Eq(7b) is re-cast as

$e^{Ah}=e^{Ah/2}{e}^{Ah/2}={\left[e^{-Ah/2}\right]}^{-1}{e}^{Ah/2}$   (8a)

and introducing the first two terms of the Taylor series for the exponential approximation

$\begin{array}{l}{e}^{-Ah/2}=I-Ah/2\equiv P^{\ast }\\ e^{Ah/2}=I+Ah/2\equiv P\end{array}$   (8b)

giving

$\psi \left(z_{n+1}\right)=P^{\ast }{}^{-1}P\psi \left(z_n\right)$ .  (8c)

The spatial approximation across a single cell then follows as

${\psi }_{n+1}=P^{\ast }{}^{-1}P{\psi }_n$ .  (8d)

Since the 1D transport equation tracks particles in either the forward or the backward directions away from the near and far boundaries, one considers the drift in each direction separately, with coupling through scattering. Of course, this is a convenient consequence of the half-range boundary conditions. Thus, we identify the forward (+) and backward (-) components as

$\psi \left(z_n\right)=\left[\begin{array}{c}{\psi }^{+}\left(z_n\right)\\ {\psi }^{-}\left(z_n\right)\end{array}\right]\simeq \left[\begin{array}{c}{\psi }_n^{+}\\ {\psi }_n^{-}\end{array}\right]$   (9a)

and when introduce into the spatial approximation

${\psi }_{n+1}=P^{\ast -1}P{\psi }_n$   (9b)

gives, on re-arranging and matrix partitioning

$\left[\begin{array}{cc}{P}_{11}^{\ast }& P_{12}^{\ast }\\ P_{21}^{\ast }& P_{22}^{\ast }\end{array}\right]\left[\begin{array}{c}{\psi }_{n+1}^{+}\\ {\psi }_{n+1}^{-}\end{array}\right]=\left[\begin{array}{cc}{P}_{11}& P_{12}\\ P_{21}& P_{22}\end{array}\right]\left[\begin{array}{c}{\psi }_n^{+}\\ {\psi }_n^{-}\end{array}\right]$ .  (9c)

The cell input and output is explicitly shown in Figure 1. By expanding the matrix multiplication.

Figure 1 Cell input and output.

$\begin{array}{l}{P}_{11}^{*}{\psi }_{n+1}^{+}+P_{12}^{*}{\psi }_{n+1}^{-}=P_{11}{\psi }_n^{+}+P_{12}{\psi }_n^{-}\\ P_{21}^{*}{\psi }_{n+1}^{+}+P_{22}^{*}{\psi }_{n+1}^{-}=P_{21}{\psi }_n^{+}+P_{22}{\psi }_n^{-}\end{array}$   (10a)

and re-arranging so that the incoming intensities are on the RHS and the outgoing on the LHS results in

$\left[\begin{array}{cc}{P}_{11}^{\ast }& -P_{12}\\ P_{21}^{\ast }& -P_{22}\end{array}\right]\left[\begin{array}{c}{\psi }_{n+1}^{+}\\ {\psi }_n^{-}\end{array}\right]=\left[\begin{array}{cc}{P}_{11}& -P_{12}^{*}\\ P_{21}& -P_{22}^{*}\end{array}\right]\left[\begin{array}{c}{\psi }_n^{+}\\ {\psi }_{n+1}^{-}\end{array}\right]$ .  (10b)

Inverting for the outgoing intensities from both boundaries gives

$\left[\begin{array}{c}{\psi }_{n+1}^{+}\\ {\psi }_n^{-}\end{array}\right]=R\left[\begin{array}{c}{\psi }_n^{+}\\ {\psi }_{n+1}^{-}\end{array}\right]$   (11a)

and the response matrix emerges as

$R\equiv {\left[\begin{array}{cc}{P}_{11}^{\ast }& -P_{12}\\ P_{21}^{\ast }& -P_{22}\end{array}\right]}^{-1}\left[\begin{array}{cc}{P}_{11}& -P_{12}^{*}\\ P_{21}& -P_{22}^{*}\end{array}\right]$ .  (11b)

Thus, we have successfully obtained an approximation to the response of an infinitesimal slab to boundary inputs. Note that the response is independent of the boundary intensities and depends only on slab properties and thickness--but we still require the response over the entire slab, so we will now add and double.

Adding and doubling

Once we find the response for a single small slab of any thickness, the interaction principle enables construction of the cumulative response for any number of slabs through adding.

We consider the response for two identical slabs as shown in Figure 2 each with response matrix R. Writing out the complete response for each slab, we have

Figure 2 Combined slabs.

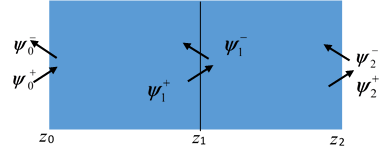
$\left[\begin{array}{c}{\psi }_1^{+}\\ {\psi }_0^{-}\end{array}\right]=\left[\begin{array}{cc}{R}_{11}& R_{12}\\ R_{21}& R_{22}\end{array}\right]\left[\begin{array}{c}{\psi }_0^{+}\\ {\psi }_1^{-}\end{array}\right]$   (12a,b)

$\left[\begin{array}{c}{\psi }_2^{+}\\ {\psi }_1^{-}\end{array}\right]=\left[\begin{array}{cc}{R}_{11}& R_{12}\\ R_{21}& R_{22}\end{array}\right]\left[\begin{array}{c}{\psi }_1^{+}\\ {\psi }_2^{-}\end{array}\right]$   (12c,d)

and expanding the products

$\begin{array}{l}{\psi }_1^{+}=R_{11}{\psi }_0^{+}+R_{12}{\psi }_1^{-}\\ {\psi }_0^{-}=R_{21}{\psi }_0^{+}+R_{22}{\psi }_1^{-}\\ {\psi }_2^{+}=R_{11}{\psi }_1^{+}+R_{12}{\psi }_2^{-}\\ {\psi }_1^{-}=R_{21}{\psi }_1^{+}+R_{22}{\psi }_2^{-}.\end{array}$    (13a,b,c,d)

Expressing the ingoing and outgoing intensities at the combined slab center interface with Eqs(13a,d) gives

$\left[\begin{array}{cc}I& -R_{12}\\ -R_{21}& I\end{array}\right]\left[\begin{array}{c}{\psi }_1^{+}\\ {\psi }_1^{-}\end{array}\right]=\left[\begin{array}{cc}{R}_{11}& 0\\ 0& R_{22}\end{array}\right]\left[\begin{array}{c}{\psi }_0^{+}\\ {\psi }_2^{-}\end{array}\right]$ ,  (14a)

and the incoming and outgoing for the second slab from Eqs(13b,c) gives

$\left[\begin{array}{c}{\psi }_2^{+}\\ {\psi }_1^{-}\end{array}\right]=\left[\begin{array}{cc}0& R_{12}\\ R_{21}& 0\end{array}\right]\left[\begin{array}{c}{\psi }_0^{+}\\ {\psi }_2^{-}\end{array}\right]+\left[\begin{array}{cc}{R}_{11}& 0\\ 0& R_{22}\end{array}\right]\left[\begin{array}{c}{\psi }_1^{+}\\ {\psi }_1^{-}\end{array}\right]$ .  (14b)

On solving Eq(14a), there results

$\left[\begin{array}{c}{\psi }_1^{+}\\ {\psi }_1^{-}\end{array}\right]=U\left[\begin{array}{c}{\psi }_0^{+}\\ {\psi }_2^{-}\end{array}\right]$ ,  (15a)

where

$U\equiv {\left[\begin{array}{cc}I& -R_{12}\\ -R_{21}& I\end{array}\right]}^{-1}\left[\begin{array}{cc}{R}_{11}& 0\\ 0& R_{22}\end{array}\right]$   (15b)

and introducing Eq(15a) into Eq(14b), gives the following combined response of two slabs:

$\left[\begin{array}{c}{\psi }_2^{+}\\ {\psi }_0^{-}\end{array}\right]=R_2\left[\begin{array}{c}{\psi }_0^{+}\\ {\psi }_2^{-}\end{array}\right]$   (16a)

with

$R_2\equiv \left[\begin{array}{cc}{R}_{11}& 0\\ 0& R_{22}\end{array}\right]U+\left[\begin{array}{cc}0& R_{12}\\ R_{21}& 0\end{array}\right]$ .  (16b)

Doubling then follows by considering the two slabs as one with response R₂ and replacing the components of R₂ with those of R₂ in Eqs(16b) to produce R₄ for the combination of two by two slabs into the response for four slabs. We continue the replacement until the entire original slab is covered. Thus, for a single slab of width a, partitioned into 2^l sub-slabs to give h = a/2^l, it takes l doublings to find the total slab response $R_2^l$  across the slab of width a.

Numerical Demonstration

Figure 3 shows the intensities exiting the boundaries. The circle

Figure 3 Exiting intensities for 2N=1600, l = 9 (15s CPU).

symbols are the 11 edits found in Table 1. The physical parameters for this case are

$\begin{array}{l}a=1\hfill \\ {\sigma }_a=0.02\hfill \\ {\sigma }_s=2\hfill \\ g=\mathrm{0.99.}\hfill \end{array}$

The plots are identical to those of Refs 2-4 and are insensitive to spatial discretization for l > 8.

As a further measure of precision, Table 1 gives a cubic spline approximation to 11 intensity edits exiting the surfaces for quadrature orders 2N =800(100)1600 and l = 9. The computational time was about 1min on a Dell Precision 2.4 Ghz PC. The last panel is in complete agreement with the results of the response matrix.² The last two columns give the relative error from consecutive panels indicating improvement with quadrature order. The most significant observation is that one achieves six-place precision and that four places are guaranteed for 2N $\ge$ 800.

The method of adding and doubling has been applied to the Fokker Planck Equation of particle transport theory with success. The method is arguably nearly the least complicated of all the transport methods. For selected edits, a spline fit delivers seven figure (six- place) precision with confirmation from the response matrix solution. While not shown, it is relatively straightforward to include heterogeneous media in the solution as demonstrated in Ref 7.

2N=800

2N=1000

2N=1200

2N=1400

2N=1600

Table 1 Cell input and output.

OLP acknowledges support from Ministerio de Ciencia e Innovación (Spain), project PID2021-122625OB-I00 with funds from MCIN/AEI/10.13039/

501100011033/ERDF, UE, and from the Xunta de Galicia (2021 GRC Gl-1563 - ED431C 2021/15).

None.

1. HC van de Hulst, Light Scattering by Small Particles, New York, Wiley, 1957; Dover, 1981.
2. BD Ganapol, Ó López Pouso. Response Matrix/Discrete Ordinates Solution of the 1D Fokker-Planck Equation, paper submitted. 2023.
3. Ó López Pouso, N Jumaniyazov. Numerical Experiments with the Fokker-Planck Equation in 1D Slab Geometry. JCTT. 2016.
4. DK Kim, P Tranquilli. Numerical Solution of the Fokker-Planck Equation with Variable Coefficients. JQSRT. 2008;109:727.
5. BD Ganapol. Particle Transport in a 3D Duct by Adding and Doubling. JCTT. 2016;46(3).
6. JE Morel. An improved Fokker-Planck Angular Differencing Scheme. Nucl Sci & Eng. 1985;89:131–136.
7. BD Ganapol. The Response Matrix Discrete Ordinates Solution to the 1D Radiative Transfer Equation. JQSRT. 2015;154:72.