One of the strongest supports for the existence of a cosmological vacuum energy density $\text{Λ}$ is given by the SN-Ia luminosities as function of the redshift z of the host galaxies, since they seem to indicate an accelerated expansion of the universe in more recent cosmic times. In this paper, we show that one in fact, however, can start out from the astronomical observations of two-point correlation functions regulating the positions of galaxies and clusters of galaxies and derive from them the average cosmic mass density in the universe. We obtained that for the scale-invariant mass distribution derived from these correlation functions we only obtain a finite mass density for a positive curvature parameter $k=+1,$ while for curvature parameters $k=0$ and $k=â\text{ˆ’}1$ one obtains vanishing cosmic mass densities. In these latter universes one consequently would find conditions for a "coasting cosmology" fulfilled which abolishes the need for a cosmic vacuum energy $\text{Λ}\text{.}$

Keywords: vacuum energy density, redshift, host galaxies, accelerated expansion, coasting cosmology

During many decades after the first Friedman-Lemaitre FLRW- cosmological models^1,2 on the basis of Einstein‘s GTR field equations^3,4 the expansion of the universe was assumed to occur as decelerated by the internal gravitation of the universe due to its matter and energy contents. In the recent decades, however, measurements of the luminosity of distant high-redshift type Ia supernovae seemed to show that these standard candles are looking fainter than could be expected on the basis of these classical cosmological models.^5–10 For the purpose to nevertheless fit these new observations with cosmological models, an artificial term - called  and denoting the dynamical effect of a cosmic vacuum energy density of completely unknown nature - has been introduced into the earlier Friedman equations with the wholesome effect of accelerating the cosmic expansion at large scales of our present epoch. Meanwhile, however, the need for this artificial enlargement of the Friedman equations has been doubted on several grounds; one is that the interpretations of luminosities of the most distant supernovae SNe-Ia may not be correctly carried out and thus misleading in the conclusions derived with them, the other is that so-called "coastal cosmology" - models , without cosmic vacuum energy density as ingredient, can in fact be proposed that can well fit the observed SNe-Ia luminosities (e.g. see Cassado, 2020).

Most recently Kang et al.,¹¹ have found evidences for an evolutionary trend in SN Ia supernova brightnesses which in principle were pointed out all the time since the publication by Tinsley¹². Their most recent studies namely seem to have shown that the brightness of standardized SN Ia supernovae is intrinsically correlated to the morphology, the mass, and the local star formation rate of the host galaxy, while in the works by Perlmutter et al.,¹³ and contemporary publishers it had been assumed that the standardized SN Ia brightness does not evolve with redshift or look-back time. This indicates the problem that the present SN Ia light curve fitters supporting the standard $\text{Λ}CDM-$ cosmological models are not taking care for a correction for this population age effect which would therefore create a serious systematic bias with increasing redshift. Just those most red-shifted SN Ia objects which presently give the strongest support for an accelerating cosmic expansion and the action of a cosmic vacuum energy would be most concerned by this bias. Meanwhile Riess et al.,¹⁴ recognized that a luminosity evolution of 25 percent over a look-back-time of 5 Gyr would be sufficient to nullify the present cosmological claims.

In this respect it is highly interesting to read in the most recent publication by Cassado (2020) that the presently discussed SNe Ia data are also fitted nicely by a universe with a "coasting cosmology" which expands according to a linear expansion model $R\left(t\right)\sim t$ with no deceleration and no acceleration, but with a permanently vanishing deceleration parameter $q=-R\ddot{R}/{\dot{R}}^2=0.$ This was already found in earlier publications by Dev et.,^15–18 This fact of an equally nice fit of a coasting universe compared to the prominent $\text{Λ}CDM-$ model concerning compatibility with SNe Ia data had already shown up clearly in a figure given in a publication by Perlmutter et al.¹⁹. But in his publication the author favored the fit by the $\text{Λ}CDM-$  model as compared to disfavored coasting model, because the latter needed an empty universe with vanishing mass density (i.e. ${\text{Ω}}_M;{\text{Ω}}_k=0)$ which obviously, in view of the present matter in the universe, cannot be assumed to prevail.

This latter conclusion was in principle also shared by Cassado (2020) who therefore was voting for quasi-coastal universe with a quasi-linear expansion like $R(t)\sim t^{(1-\gamma )}$ with $\gamma \ll 1.$ But it should be pointed out here that an empty universe neither is in fact a severe need of the coastal universe, nor can a vanishing of the average cosmic mass density simply be excluded as we are going to show in the following part of the paper. To our knowledge one of the first authors presenting a coastal cosmology was Kolb²⁰ who introduced a special form of matter which he called K-matter with an equation of state $p_K=-\left(1/3\right){\rho }_K$ in between the poly-tropic behavior of photonic matter and massive matter. For this form of matter the second Friedmann equation delivers

$\frac{\ddot{R}}{R}=-\frac{4\pi G}{3}\left({\rho }_K+3p_K\right)=0$ (1)

It can be shown that this K-matter leads to a density decrease by ${\rho }_K\sim R^{-2}$ and by its polytropic behaviour $\rho K+3pK=0$ induces a coasting universe.

This form of a K-matter unfortunately is not a physically very handy and easy to understand form of matter and thus may be disfavored for that reason in offering a physically reliable cosmological solution. As was shown, however, in papers by Fahr²¹ and Fahr²² and this unconventional sub-adiabatic behavior of density with the scale $R$ of the universe is naturally obtained for a Machian form of scale-related masses of cosmic particles with $m\sim R$ which then evidently with $\rho \sim R^{-2}$ leads to a coasting cosmology. But as we shall show in the following part of the paper, one does not need to believe in such a Machian mass behavior tuning the cosmic masses with the size $R$ of the universe, but it can be shown that an empty universe with vanishing mass density ${\rho }_U=0$ creating a coasting cosmology is in fact physically reasonable - even in view of the cosmic masses seen around us, if the universe has a scale-invariant hierarchical structuring.

In the afore presented argumentation²⁵ it became obvious, that the theoretical interpretation of distant high-redshift SN1a luminosity data is well possible, instead by the new $\text{Λ}CDM-$ cosmological models, as well on the basis of a coasting expansion cosmology^23,24 with a linear expansion of the scale of the universe with cosmic time t according to $R\left(t\right)\sim t.$ The attractive advantage on one hand in the use of these latter cosmological models is that neither dark matter nor dark energy is required (i.e ${\text{Ω}}_D={\text{Ω}}_{\text{Λ}}=0)$ for the interpretation, the disadvantage on the other hand, as seen by many of the present main-stream cosmologists, is that such coasting models as given by Kolb et al.,^20–27 have to assume an empty energy-momentum tensor $T_{ik}$ for the universe, i.e. a tensor with vanishing ingredients at all cosmic times t. Especially such coasting universes should have either, as we are going to show, the special Machian property of scale-related cosmic masses leading to vanishing mass densities at the largest scales, or the property that mass density ${\rho }_U$ is zero at all relevant cosmic times due to reasons which are connected with a full compensation of contributions from masses through those from pressures in the universe.

Most cosmologists are hesitating to accept this rather unlikely balance in the $T_{ik}-$ ingredients leading to a coasting universe. This zero-mass universe seems to be too much an artifact like the assumption of cosmic vacuum energy $\text{Λ}$ is too. In the following section, however, just for that purpose, we want to introduce a universe leading to a vanishing cosmic mass density ${\rho }_U\to 0!$ at the largest cosmic distances without such artifacts which in contrast is even supported by astrophysical measurements as we are going to show below.

We start from the astronomical observations carried out by Bahcall et al.,^28,29 and or equally well in more recent times by Sylos-Labini et al.,³⁰ and or Sylos-Labini³¹ and take their two-point correlation function $\xi \left(l\right)$ denoting the probability to find other stellar objects at a distance $l$ from any other arbitrarily taken stellar object. The quantity $l$ has to be considered as the so-called distance parameter taken by astronomers to be identical with the redshift distance, making it evidently a cosmologically biased quantity. From this star-correlation function $\xi \left(l\right)$ we will deduce in the following an associated model for the underlying cosmic matter density distribution ${\rho }_U={\rho }_U\left(l\right).$ This we first did for a different aspect in a recent paper Fahr etal.,³². We use the well confirmed correlation function $\xi \left(l\right)$ based on astronomical observations of the visible star and galaxy constellation which is surrounding us seen from our cosmic vantage point, - and, according to the generally assumed cosmological principle, also should surround every other cosmic vantage point in an analogous and equivalent manner, unless the generally accepted, sacrosanct cosmological principle would turn out to be violated,- in which case, however, all the other Robertson-Walker cosmologies would as well become invalid, and even taken broader, all cosmology had to be given up.

This two-point correlation function $\xi \left(l\right)$ defines the probability to find another star (or galaxy) at a distance lfrom our arbitrary standpoint and, based on astronomical observations, is expressed in the following mathematical form:

$\xi \left(l\right)={\xi }_0\cdot {(\frac{l_0}{l})}^{\alpha }$      (2)

where ${\xi }_0$ is a reference value valid at the reference distance$l_0.$ The correlation index ${}^{\alpha }$ has been observationally determined by Bahcall et al.²⁸ with$\alpha =1.8$ By the way, as we do show in the appendix, this above hierarchic distribution of stars naturally explains why no Olbers Paradox (Paradox of the dark night sky!) has to be expected in such a universe.

An interesting problem connected with the above mentioned clustering is the cosmologically important point, that the validity of the above correlation function can evidently also be interpreted as an expression for the structured stellar mass density $\rho =\rho \left(l\right)$ or stellar mass density distribution of surrounding stars or galaxies in our cosmic environment. In this view it also expresses a standpoint-oriented mass density distribution $\rho =\rho \left(l\right)$ when it is recognized that the mass $dM\left(l\right)$ in this case is closely associated with the number of stars with a typical average stellar or galactic mass $m_0$ on a spherical shell at distance $l,$ and is given for a Euklidean space geometry (i.e. a flat universe with $k=0$ ) by

$dM\left(l\right)=4\pi l^2{m}_0{\xi }_0{(\frac{l_0}{l})}^{\alpha }dl=4\pi l^2{\rho }_0\cdot {(\frac{l_0}{l})}^{\alpha }dl$ (3)

with ${\rho }_0$ denoting the hierarchy-typical reference value of mass density.

Bahcall and Chokski²⁹ do furthermore point out the astonishing fact that the general type of the above mentioned two-point correlation function $\xi \left(l\right)$ is observationally confirmed as well for galaxy correlations, as for cluster correlations, as also for super-cluster correlations, with the difference that only the reference scale $l_0$ and the reference probability ${\xi }_0$ or mass density ${\rho }_0$ have to be adapted from the galaxy-case up to the super-cluster case, while as a surprise the same correlation index of ${\alpha }_G={\alpha }_C={\alpha }_{SC}=1.8$ is reappearing as a number common for all these hierarchies (i.e. scale invariant structuring!).

To comprehend and correctly describe space at the largest achievable distances $l_{SC,0}$ of the order $100Mpc$ or more, we take the largest hierarchy, i.e. super-clusters, and use the corresponding $SC-SC$ correlation function. Connected with that correlation the following, associated mass increment with distance $l$ is given:

$dM\left(l\right)=4\pi l^2{\rho }_{SC,0}\cdot {(\frac{l_{SC,0}}{l})}^{{\alpha }_{SC}}\cdot dl$                        (4)

In order to address scientifically correct the largest achievable cosmic distances $l\simeq R$ , with R denoting the scale of the universe, we have also to pay attention to the prevailing cosmic space geometry conditions and need to face the situation that, in order to keep our considerations open to the widest generality, that we are perhaps embedded not in a Euklidean universe, but in a curved general-relativistic space-time geometry. We for the sake of this generality should pay attention to the fact that the radial distance parameter $l$ , in the Robertson-Walker approximation of the cosmic geometry, is transformed into a geometrical distance $r\left(l\right)$ given by the following function:^33,34

$r\left(l\right)=l\cdot {(1+k{l}^2)}^{-1}$                  (5)

i.e. the spherical area associated to the distance parameter $l$ then is $\text{Φ}\left(l\right)=4\pi r^2\left(l\right)$ where $k$ denotes the cosmic curvature parameter. The latter e.g. is determined by looking for the best fitting cosmological FLRW-model³⁵ which supports the value $k\simeq 0$ . This latter uncurved cosmological model is, however, associated with and enforced by specifically equilibrated average cosmic $T_{ik}$ -ingredients like ${\text{Ω}}_{\text{Λ}},{\text{Ω}}_M,{\text{Ω}}_D$ . These latter ingredients, however, under the perspectives given here, are shown to be highly problematic quantities. Nevertheless and besides of that, anticipating the indicated curvature value $k$ as an apriori input, one can then take account of this above geometric distance transformation by bringing the above formula for $dM\left(l\right)$ into the following form:$dM\left(l\right)=4\pi l^2\cdot {(1+k{l}^2)}^{-2}\cdot m_{SC,0}{\xi }_{SC,0}\cdot {(\frac{l_{SC,0}}{l})}^{\alpha }\times$          

$\times \frac{\left(1-k{l}^2\right)}{{(1+k{l}^2)}^2}dl$                         (6)

and after a little rearrangement of the terms.

$dM\left(l\right)=4\pi {\rho }_{SC,0}\cdot \left(\frac{l_{SC,0}}{l}{)}^{\alpha }\cdot \frac{\left(1-k{l}^2\right)}{{(1+k{l}^2)}^4}{l}^{2}dl\right]$                           (7)

The cosmic curvature parameter $k$ can be restricted to values of $k=0$ or $k=\pm 1$ , if $l$ is scaled with the cosmic scale parameter $R=R\left(t\right)$ by $k=K\cdot R^2$ , $K$ being the cosmic curvature scalar or the contracted Ricci tensor $K=R_i^i$ . Therefore, besides the Euklidean case $k=0$ , favored by Benett et al.,³⁵ one should also consider the following two more options:

$dM\left(l\right)=4\pi {\rho }_{SC,0}{l}_{SC,0}^{\alpha }\cdot \left[\frac{\left(1\mp \frac{l^2}{R^2}\right)}{{(1\pm \frac{l^2}{R^2})}^4}{l}^{2-\alpha }dl\right]$                             (8)

After this inspection one can then state that the expression for the average cosmic density in such a hierarchically structured universe, for instance with $k=\pm 1$ finally takes the following form:

$\rho \left(l\right)=\frac{M\left(l\right)}{V\left(l\right)}4\pi {\rho }_{SC,0}{l}_{SC,0}^{\alpha }\frac{{\displaystyle \underset{0}{\overset{\lambda }{\int }}\left[\frac{\left(1\mu \frac{{\lambda }^2}{P^2}\right)}{{(1+\frac{{\lambda }^2}{P^2})}^2}{\lambda }^{2-\alpha }\delta \lambda \right]}}{{\displaystyle \underset{0}{\overset{\lambda }{\int }}\left[\frac{\left(1\mu \frac{{\lambda }^2}{P^2}\right)}{{(1+\frac{{\lambda }^2}{P^2})}^2}{\lambda }^2\delta \lambda \right]}}=4\pi {\rho }_{SC,0}\frac{l_{SC,0}^{\alpha }}{R^{\alpha }}\frac{{\displaystyle \underset{0}{\overset{\Xi }{\int }}\left[\frac{\left(1\mu {\xi }^2\right)}{{\left(1+{\xi }^2\right)}^4}{\xi }^{2-\alpha }\delta \xi \right]}}{{\displaystyle \underset{0}{\overset{\Xi }{\int }}\left[\frac{\left(1-{\xi }^2\right)}{{\left(1+{\xi }^2\right)}^4}{\xi }^2\delta \xi \right]}}$                 (9)

In Figure 1 we show the quantity $\rho \left(l\right)$ as function of $l$ , for all relevant cosmic geometries, i.e. $k=\pm 1$ and $k=0$ .

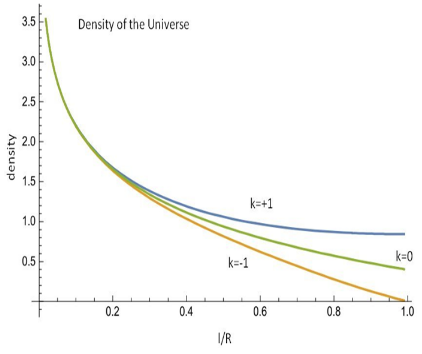
Figure 1 Shown is the average cosmic density $\rho \left(1\right)$ in units of the super-cluster density ρSC,0 as function of the averaging scale l/R for three different cosmic geometries characterized by curvature values k = 0 and k =±1.

As one can see in Figure 1 there exists only one model which leads to a finite cosmic density at large scales, namely for the positively curved universe with $k=+1$ ; the other two models with $k=0$ $k=-1$ show cosmic densities which fall below every lower density limit with increasing scales, i.e. at largest scales they fall down to a density value of ${\rho }_U\simeq 0!$

Coming back to the question whether coasting universes should be considered as a physical possibility, one can thus see from the above considerations that in universes with curvatures $k=0$ or $k=-1$ and a hierarchical mass distribution one finds the appropriate prerequisites fulfilled for a coasting universe with a vanishing average cosmic mass density, i.e. ${\rho }_U=0$ !, despite the visible stars and galaxies around us. One more cosmological possibility might perhaps need to be considered here, namely that the hierarchical structuring of masses in the universe which was considered in the above calculation could perhaps also be a time-invariant cosmic structuring, meaning that even though the universe undergoes an expansion in cosmic time, its hierarchical structuring endures or persists. Of course an expanding hierarchical universe must also change its mass density, however in such a way that the hierarchical structuring of matter persists, i.e. a time-invariant scale-invariance under these auspices must be considered. This form of a structure persistence is given when only the reference density of the reference structure undergoes an associated cosmological time-dependence. Under these auspices the mass increment $dM\left(l\right)$ derived above would then instead now be given by the expression:

$dM\left(l\right)=4\pi l^2{\rho }_{SC,0}\left(t\right)\cdot {(\frac{l_{SC,0}\left(t\right)}{l})}^{{\alpha }_{SC}}\cdot dl$                              (10)

One may assume that the dimension $l_{SC,0}\left(t\right)$ of super-clusters increases with cosmic time $t$ like the cosmic scale parameter, i.e.$l_{SC,0}\left(t\right)\sim R\left(t\right).$ The reference value for the super-cluster density on the other hand most probably scales according to

${\rho }_{SC,0}\left(t\right)={\rho }_{SC,0}\cdot {(R_0/R\left(t\right))}^3$                                (11)

which then all-together leads to a mixed expression in time $t$ and distance $l$ given by:

$dM\left(l\right)=4\pi l^2{\rho }_{SC,0}\cdot {(R_0/R\left(t\right))}^3{(\frac{R\left(t\right)}{l})}^{{\alpha }_{SC}}\cdot dl$                     (12)

and again herewith brings up the already well-identified problem that in the cosmological GTR field equations time-averaging and space-averaging cannot be exchanged.^36–38 One way to overcome this problem in the above described case would be to connect distances of cosmic masses with the time it takes to bring over the information on their mass locations by their gravity signals, i.e. gravitons, through the velocity c of light by correspondingly retarding the relevant evolutionary state of the universe. This would then lead to the easily integrable expression:

$dM\left(l\right)=4\pi l^2{\rho }_{SC,0}\cdot {(\frac{R_0}{R\left(t_0-l/c\right)})}^3{(\frac{R\left(t_0-l/c\right)}{l})}^{{\alpha }_{SC}}\cdot dl$                     (13)

and shows that influences of the distant matter structures now are attaining a cosmologically historical pronunciation making the universe by this view a really authentic space-time unity. To further evaluate the above expression one would need to know the scale evolution $R=R\left(t\right)$ in this universe. The latter, however, depends on the prevailing cosmic energy ingredients as especially the average mass density of cosmic matter $\rho \left(l\to \infty \right)$ which, however, is only found from the integration of expression (13). Not knowing in advance what the integrated expression starting with Equ. (13) will deliver, we can make two alternative assumptions in advance:

1. The average mass density is positive and finite with $\rho \left(l\to \infty \right)={\rho }_{\infty }.$

or

2. The average mass density is $\rho \left(l\to \infty \right)=0$

The correctness of the assumption a) or b) will then be proven a posteriori after having carried out the necessary integrations. Starting with case a) we would be based on a matter-dominated flat universe (k=0) the scale evolution of which is known to follow the law $R\left(t\right)\sim t^{2/3}$ .³⁹ Thus in this case one has

$R\left(t\right)=R_0\cdot {(\frac{t}{t_0})}^{\frac{2}{3}}=R_0\cdot {(\frac{t_0-l/c}{t_0})}^{\frac{2}{3}}$                         (14)

when using $R\left(t\right)=R\left(t_0-l/c\right)$ with$t=t_0-l/c.$ This then leads Equ. (13) to:

$dM\left(l\right)=4\pi l^2{\rho }_{SC,0}\cdot {({(\frac{t_0}{t_0-l/c})}^{\frac{2}{3}})}^3{(\frac{R_0}{l})}^{{\alpha }_{SC}}\times$               

$\times {(\frac{t_0-l/c}{t_0})}^{\frac{2{\alpha }_{SC}}{3}}dl$                  (15)

or      

$dM\left(l\right)=4\pi l^2{\rho }_{SC,0}\cdot {(\frac{1}{1-l/c{t}_0})}^2{(\frac{R_0}{l})}^{{\alpha }_{SC}}\times$

$\times {(1-l/c{t}_0)}^{\frac{2{\alpha }_{SC}}{3}}dl$               (16)

We now use the substitution$z=1-l/c{t}_0,$ hereby keeping in mind that the relation $t=t_0-l/c$ leads to $l\left(t=0\right)=c{t}_0$ and $l\left(t=t_0\right)=0$ which means $z=0$ for $l\left(t=0\right)=c{t}_0$ and $z=1$ for$l\left(t=t_0\right)=0.$ Furthermore, dl is given by$dl=-c{t}_{0}dz.$ This finally results in the following equation:

$M=4\pi {(c{t}_0)}^3{(\frac{R_0}{c{t}_0})}^{{\alpha }_{SC}}{\rho }_{SC,0}\times$               

$\times \underset{0}{\overset{1}{{\displaystyle \int }}}{(1-z)}^{\left(2-{\alpha }_{SC}\right)}{z}^{\left(\frac{2}{3}{\alpha }_{SC}-2\right)}dz$                   (17)

The retarded average density $\rho \left(l\to R\right)$ is then given by:               

$\rho \left(R\right)=\frac{M\left(R\right)}{V\left(R\right)}=4\pi {(c{t}_0)}^3{(\frac{R_0}{c{t}_0})}^{{\alpha }_{SC}}{\rho }_{SC,0}\times$

$\times \frac{{(c{t}_0)}^3{(\frac{R_0}{c{t}_0})}^{{\alpha }_{SC}}{\rho }_{SC,0}\cdot {{\displaystyle \int }}_0^1{(1-z)}^{\left(2-{\alpha }_{SC}\right)}{z}^{\left(\frac{2}{3}{\alpha }_{SC}-2\right)}dz}{{{\displaystyle \int }}_0^{c{t}_0}{l}^{2}dl}$                             (18)

Now, with the typical correlation index ${\alpha }_{SC}=1.8$ mentioned before in section 2 of this paper, and expressing the volume $V$ by $\frac{4\pi }{3}{(c{t}_o)}^3$ we get:

$\rho =3{(\frac{R_0}{c{t}_0})}^{{\alpha }_{SC}}{\rho }_{SC,0}\cdot \underset{0}{\overset{1}{{\displaystyle \int }}}\frac{{(1-z)}^{0.2}}{z^{0.8}}dz\approx$

$\approx 3{(\frac{R_0}{c{t}_0})}^{{\alpha }_{SC}}{\rho }_{SC,0}\cdot 4.75$                          (19)

This shows that in case a) for the universe with a time-invariant and scale-invariant matter structuring one obtains a finite and positive average mass density which then a posteriori also justifies the use of the scale evolution law $R\sim t^{2/3}$ valid for the matter-dominated universe.

Case b):

For this case we in advance want to assume that one obtains a vanishing average cosmic mass density with $\rho \left(l\to R\right)=0.$ Consequently the scale evolution law for this universe is a "coasting cosmology evolution" given by the law $R\left(t\right)\sim t$ , and by carrying out the analogue calculation of the mass density as above for this universe we should be able to a posteriori prove that in this case the associated average density in fact is $\rho \left(l\to R\right)=0$ !But in fact we have carried out this alternative integration for case b) and it turns out that the resulting average mass density is again positive and even greater than in case a). But this then means that the use of the coasting cosmology scale law $R\left(t\right)\sim t$ is not a posteriori justified in this case b).

Let us consider now a single mass m embedded in a homogeneous, infinite universe. Then one may want to study the question: What will happen in case this mass m has a peculiar motion by a certain velocity $\overrightarrow{U}$ with respect to the local standard of rest of the ambient universe? How does this velocity behave in time? For the case that this peculiar motion is changing in time by an amount$\overrightarrow{b}=d\overrightarrow{U}/dt,$ a local force must be identifiable causing this de-/ac-celeration$\overrightarrow{b}.$ In the absence of any viscous forces or electromagnetic forces etc. one may be able to reduce the force candidate to some effective force caused by the net gravitational pull of all the cosmic masses surrounding this peculiar mass , and one should be able to quantify a locally acting force as due to the net gravitational force of the ambient universe influencing this peculiar mass m at its peculiar motion $\overrightarrow{U}.$

In order to study this problem more quantitatively one could follow the approach that already was used by Thirring⁴⁰ or Soergel-Fabricius⁴¹ to study centrifugal forces acting on a mass rotating with respect to the rest of a universe with a homogeneous mass distribution. The idea there was to represent the mass of the universe as a system of congruent spherical mass shells. While Thirring⁴⁰ or later Fahr²⁴ and along this way had faced the problem of a rotating central mass to study the origin of cosmic centrifugal forces, we here instead have to look for a solution of the problem connected with a central mass m in peculiar motion$\overrightarrow{U}$ with respect to the rest of the universe. Question: Would this motion persist unchanged in time or will it undergo a temporal change and by what amount would it do it?

To answer this question on the basis of post-Newtonian SRT gravity one has to realize that due to the finite propagation speed of gravitons, communicating the surrounding mass constellation by gravitons to the position of the moving central mass $m$ with the velocity of light$c,$ the individual mass sources $\delta M_U$ of the surrounding gravity field of the universe are all effectively acting from "apparently retarded" positions when judged from the position of the moving central mass (a phenomenon analogous to stars appearing at positions shifted from their true positions due to the motion of the observer: i.e. stellar aberration). That means, if the mass element$\delta M_U$ on a spherical mass shell is seen by a central object at rest under an angle$\theta ,$ it instead acts effectively from the aberration angle $\theta \text{'}$ on the central object, when the latter moves with the velocity$\overrightarrow{U}$ with respect to the local standard of rest. According to STR relations these two angles are connected by the following STR Doppler relation:

$\text{cos}\theta \text{'}=\frac{cos\theta +\beta }{1+\beta cos\theta }$                  (20)

where $\beta$ is given by $\beta =U/c.$

Assuming a homogeneous and constant cosmic mass density distribution with$\rho ={\rho }_U,$ then one arrives at the following effective gravitational force $K_{\parallel }=\left({\overrightarrow{K}}_U\cdot \overrightarrow{U}\right)/U,$ aligned with the direction of the peculiar velocity $\overrightarrow{U},$ acting in the direction $\left(-\overrightarrow{U}\right)$ on the central mass $m,$ due to the net gravitational pull of the surrounding cosmic mass assembly of the universe:         

$K_{\parallel }=-\underset{0}{\overset{R_{\text{max}}}{{\displaystyle \int }}}d{R}_U\underset{0}{\overset{\pi }{{\displaystyle \int }}}d\theta \times$

$\times {\displaystyle \underset{0}{\overset{2\pi }{\int }}d\varphi \rho U{R}_U^2}\frac{Gm}{R_U^2}\cos \theta \sin \theta$                                (21)

evidently leading to

$K_{\parallel }=-2\pi {\rho }_{U}Gm\underset{0}{\overset{R_{\text{max}}}{{\displaystyle \int }}}\delta {{\rm P}}_{{\rm Y}}{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \theta \text{'} sin\theta d\theta }$                               (22)

and to

$K_{\parallel }=-2\pi {\rho }_Y\Gamma \mu R_{\max }{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \theta \text{'}\sin \theta d\theta }$                      (23)

This expression already in this form reveals that $K_{\parallel }$ can only be a finite quantity, if the product ${\rho }_U{R}_{\text{max}}$ stays finite, requiring that the average density should be either strictly zero or proportional to ${\rho }_U\sim R_{\text{max}}^{-1}$ in an infinite universe.

On the other way, with the average cosmic density ${\rho }_U,$ expressed through the total mass $M_U$ for the Euclidean universe, given by${\rho }_U=\left(3/4\pi \right)M_U/R_{\text{max}}^3,$ - $R_{\text{max}}$ being the radius of the matter-filled universe -, leads to the following expression:

$K_{\parallel }=-\frac{3}{2}Gm\frac{M_U}{R_{\max }^2}{\displaystyle \underset{0}{\overset{\pi }{\int }}\frac{\cos \theta +\beta }{1+\beta \cos \theta }}\sin \theta d\theta$                  (24)

and, to obtain a finite quantity$K_{\parallel },$ would then require $M_U\sim R_{\text{max}}^2$ . For a positively/negatively curved space $k=+1/-1$ we would instead find the following relation:

${\rho }_U=\left(3/4\pi \right)M_U/(R_{\text{max}}^3-\left(1/5\right)\left(k/r^2\right)r^5+\mathrm{...})=\left(3/20\pi \right)M_U/R_{\text{max}}^3/\left(18/20\pi \right)M_U/R_{\text{max}}^3.:$

By substituting coordinates $\theta$ by $x=\text{cos}\theta$ one obtains:

$K_{\parallel }=-\frac{3}{2}Gm\frac{M_U}{R_{\max }^2}{\displaystyle \underset{1}{\overset{-1}{\int }}\frac{x+\beta }{1+\beta x}}dx$                               (25)

$K_{\parallel }=\frac{3}{2}Gm\frac{M_U}{R_{\max }^2}{\displaystyle \underset{1}{\overset{-1}{\int }}\left[\frac{x}{1+\beta x}+\frac{\beta }{1+\beta x}\right]}dx$                               (26)

which can be further integrated to yield:          

$K_{\parallel }=\frac{3}{2}Gm\frac{M_U}{R_{\text{max}}^2}[\frac{1}{{\beta }^2}\times \underset{1+\beta }{\overset{1-\beta }{{\displaystyle \int }}}\frac{\left(y-1\right)dy}{y}+\left[n\left(1-\beta \right)-\ln \left(1+\beta \right)\right]$                              (27)

and:

$K_{\parallel }=-\frac{3}{2}Gm\frac{M_U}{R_{\max }^2}[\frac{1}{{\beta }^2}{\displaystyle \underset{+\beta }{\overset{-\beta }{\int }}\frac{\zeta \delta \zeta }{\zeta +1}}+\ln \frac{1-\beta }{1+\beta }]$                               (28)

or finally leading to:

$K_{\parallel }\left(\beta \right)=\frac{3}{2}Gm\frac{M_U}{R_{\text{max}}^2}\left[\frac{1-{\beta }^2}{{\beta }^2}\text{ln}\left(\frac{1+\beta }{1-\beta }\right)-\frac{2}{\beta }\right]$                         (29)

From Figure 2 it becomes evident that this force $K_{\parallel }$ is vanishing for $\beta \to 0$ which is a natural requirement, since for an object at rest, the masses of the homogeneous universe around, due to symmetry reasons, should not induce any net force. Interestingly enough, one can also calculate the typical cosmic braking period $\tau \left(\beta \right)=-\beta /d\beta /dt$ until differential motions die out given by:

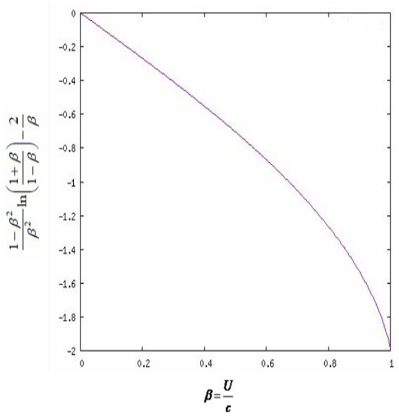
Figure 2 The bracket term $\left[\frac{1-{\beta }^2}{{\beta }^2}\text{ln}\left(\frac{1+\beta }{1-\beta }\right)-\frac{2}{\beta }\right]$ of the cosmic braking power$K_{\parallel }$ in Eq. (29) as function of $\beta =U/c$ decelerating peculiar motions U of stars or galaxies in a universe with a constant value of $frac{M}_U{R}_{\text{max}}^2$ .

$\tau \left(\beta \right)=\frac{2}{3}\frac{R_{\text{max}}^2}{G{M}_u}\frac{\beta }{\left[\frac{1-{\beta }^2}{{\beta }^2}\text{ln}\left(\frac{1+\beta }{1-\beta }\right)-\frac{2}{\beta }\right]}$                                (30)

which for $M_U\sim R_{\text{max}}^2$ is a finite time period and in general determines the time after which all peculiar galaxy motions should have died out in the universe, i.e. only the rigorous Hubble motion continues to exist in such a "crystalline" universe after that period. This time evidently is dependent on the cosmic value prevalent for $R_{\text{max}}^2/M_U$ or equivalently for${\rho }_U{R}_{\text{max}}.$ If these latter values are finite, then the cosmic braking period $\tau \left(\beta \right)$ is finite too, and when the universe has an age ${\tau }_H=1/H=R/\dot{R}$ larger than this period, then all peculiar motions in this universe should have died out.

In an infinite universe $R_{\text{max}}\to \infty$ with finite density the expression for $K_{\parallel }\left(\beta \right)$ can only be finite, if the density in such a universe scales with${\rho }_U\sim 1/R_{\text{max}}.$ Otherwise, if such a physical connection cannot be supported and required with physical sense, the density in such a universe should then simply vanish; i.e.${\rho }_U=0!,$ as it does in a scale-invariant hierarchically structured universe (see Figure 1 in the section above for $k=0;k=-1).$

This above consideration may become a little bit more complicated, if also hereby the problem of the expanding universe has to be taken into account in this problem. Then looking into larger distances may mean that evolutionary earlier cosmic phases of cosmic matter distribution are determining the considered gravitational influences. This means that, with growing distances and longer times it takes to communicate through gravitons the cosmic mass positions to the local position, gravitational influences of earlier evolutionary states of the universe with a higher mass density physically come into the game. This may be taken into account by modifying the above expression for the braking power by:

$K_{\parallel }=-2\pi Gm{\displaystyle \underset{0}{\overset{\infty }{\int }}{\rho }_Y}\left(\tau \right)\delta R_U{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \theta \sin \theta d\theta }$                              (31)

leading by inclusion of the cosmologically retarded densities to the following expression:

$K_{\parallel }=-2\pi Gm{\displaystyle \underset{0}{\overset{\infty }{\int }}\rho \left(t_0-R_u/c\right)}d{R}_U{\displaystyle \underset{0}{\overset{\pi }{\int }}\cos \theta \text{'} sin\theta d\theta }$                                (32)

leading with $R_{U0}=R_U(t_0)$ to:       

$K_{\parallel }=-2\pi Gm\rho U0{\displaystyle \underset{0}{\overset{\infty }{\int }}(\frac{R_{U0}}{R_U(t_0-R_u/c}}{)}^{3}d{R}_U\times$

$\times \underset{0}{\overset{\pi }{{\displaystyle \int }}}\text{cos}\theta \text{'}\text{sin}\theta d\theta$                   (33)

$K_{\parallel }=-{\displaystyle \underset{0}{\overset{\infty }{\int }}dRU{\displaystyle \underset{0}{\overset{\pi }{\int }}d\theta }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\varphi }.{\rho }_U{R}_U^2\frac{Gm}{R_U^2}\cos \theta \text{'} \sin \theta$                        (34)

This expression, in a hierarchically structured universe, would write the following way:

$K_{\parallel }=-Gm{\displaystyle \underset{0}{\overset{\infty }{\int }}{\rho }_U}d{R}_U{\displaystyle \underset{0}{\overset{\pi }{\int }}\delta \theta }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\varphi .\cos \theta \text{'}\sin \theta }$                              (35)

and with the differential mass increase in a hierarchic universe given by:

$dM\left(l\right)=4\pi {\rho }_{SC,0}\cdot \left(\frac{l_{SC,0}}{l}{)}^{\alpha }\cdot \frac{\left(1-k{l}^2\right)}{{(1+k{l}^2)}^4}{l}^{2}dl\right]$                           (36)

then would lead to:       

$\begin{array}{l}{K}_{\parallel }=-Gm{\displaystyle {\int }_0^{1}4\pi \rho SC,0 . [(\frac{l_{SC,0}}{l}}{)}^{\alpha }\times \\ \times \frac{(1-k{\left(l/R_u\right)}^2)}{1+k{\left(l/R_u\right)}^2)}dl]{\displaystyle {\int }_0^{\pi }d\theta }{\displaystyle \underset{0}{\overset{2\pi }{\int }}d\varphi . \cos \theta \text{'} . \sin \theta }\end{array}$                          (37)

showing that under a hierarchically structured universe this force $K_{\parallel }$ in any case is finite.

In the above sections the asymmetric action of cosmic mass distributions on a single mass m with a peculiar motion by a velocity $U$ with respect to the rest of the universe (i.e. local standard of rest) was considered, and with $\beta =U/c$ the following expression has been derived for the net gravitational force that acts on this mass

$K_{\parallel }\left(\beta \right)=\frac{3}{2}Gm\frac{M_U}{R_{max}^2}\left[\frac{1-{\beta }^2}{{\beta }^2}\text{ln}\left(\frac{1+\beta }{1-\beta }\right)-\frac{2}{\beta }\right]$                         (38)

As one can see in Figure 2 this expression can also be evaluated for$\beta \to 1,$ i.e. relativistic particles or photons moving with the velocity$U=c.$ For photons one would obtain the following result:

$K_{\parallel }\left(\beta =1\right)=\frac{3}{2}Gm\frac{M_U}{R_{\text{max}}^2}\cdot [-2]$                  (39)

Talking about photons here, one can interpret this equation as stating that the temporal change of the momentum of the photon $d{P}_{\nu }/dt=d/dt\left(h\nu /c\right)$ is given as the function of the mass of the photon, i.e.$m=h\nu /c^2$ by

$\frac{h}{c}\frac{d\nu }{dt}=-3G\frac{h\nu }{c^2}\frac{M_U}{R_{\text{max}}^2}$                             (40)

or describing the change of the photon frequency $\nu$ by

$\frac{d\nu }{dt}=-3G\frac{\nu }{c}\frac{M_U}{R_{\text{max}}^2}$                  (41)

yielding the following solution for the cosmic frequency shift of cosmic photons during the course of cosmic time:

$\nu \left(t\right)=\nu \left(t_0\right)\text{exp}\left[-3G\frac{M_U}{c{R}_{\text{max}}^2}\left(t-t_0\right)\right]$                     (42)

Interestingly enough, this result must be interpreted as a photon redshift which is caused by the asymmetric action of cosmic gravity during the mere passage time or travel distance of the photon since its emission. This cosmic redshift would thus be a pure indicator of the distance which the photon has covered since its emission, and would not have anything to do with the cosmic expansion dynamics of the universe. Galactic photon redshifts could thus not be ascribed to the recession velocity of the photon emitting galaxies. We now use $\lambda \nu =c$ and ${\lambda }_0{\nu }_0=c$ for a photon with wavelength $\lambda$ and frequency $\nu$ as well as $\lambda ={\lambda }_0(1+z)$ at a given redshift $z$ and the above mentioned travel distance $D=c(t-t_0)$ to get:

$1+z=\text{exp}\left[3G\frac{M_U}{c{R}_{\text{max}}^2}\left(t-t_0\right)\left]=\text{exp}\right[3G\frac{M_U}{c^2{R}_{\text{max}}^2}D\right]$                               (43)

or:

$\frac{M_U}{R_{\text{max}}^2}=\frac{c^2}{3GD}ln\left(1+z\right)$                            (44)

With $z=0.5$ und $D=300Mpc\approx {10}^{25}m$ as typical given values for a galaxy³³ the expression $M_U/R_{\text{max}}^2$ yields:     

$\frac{M_U}{R_{\text{max}}^2}\approx \frac{{(3\cdot {10}^8)}^2}{3\cdot 6.67\cdot {10}^{-11}\cdot {10}^{25}}ln\left(1.5\right)\frac{kg}{m^2}\approx$

$\frac{300}{6.67}0.4\frac{kg}{m^2}\approx 18\frac{kg}{m^2}$                             (45)

With $z=0.1$ and $D=500Mpc$ we get $\approx 3\frac{kg}{m^2}.$

On the other hand, we can also calculate the expression $M_U/R_{\text{max}}^2$ with typical values of $M_U\approx {10}^{53}kg$ and $R_{max}\approx c{t}_o\approx {10}^{26}m$ ³³ - with t₀ the age of the universe - to retrieve:

$\frac{M_U}{R_{\text{max}}^2}\approx \frac{{10}^{53}}{{10}^{52}}=10\frac{kg}{m^2}$                             (46)

which is a very satisfying result since it is in the same order of magnitude.

 In this paper we have picked up the idea of Cassado²⁵ that a "coasting universe", i.e. a universe with an unaccelerated scale expansion velocity$\dot{R}=const,$ may well explain the redshifts of distant supernovae SN-Ia. These puzzling redshifts had led authors like Perlmutter et al.,^5–10 to the conclusion that in the more recent cosmic evolution times the universe shows an accelerated expansion and thus requires a non-vanishing positive vacuum energy density$\text{Λ}\text{.}$ In order, however, to accept a coasting universe one would need to see very specific cosmic conditions as fulfilled. Kolb²⁰ was the first to study such conditions and concluded that, for this case to be fulfilled, pressure $P$ and matter density $\rho$ of the relevant cosmic matter should be related by a poly-tropic relation of the form$P=-\left(1/3\right)\rho .$ This then, as shown by the second Friedman equation, leads to a vanishing scale acceleration $\ddot{R}.$ The needed poly-tropic relation, as Kolb²⁰ showed, would characterize a form of matter behavior between baryonic and photonic matter, called by him "K-matter" (Koino-matter). In more recent papers by Fahr et al.,^21,22 it was then shown that a coasting universe also results for the Machian case of scale-related cosmic masses leading to a mass density behavior according to$\rho \propto R^{-2}.$ In this paper here we looked into a further possibility to have a coasting universe realized, namely by having a vanishing cosmic mass density. This, at a first glance, looks quite unlikely in view of the stars around us, but as we do show here, such an "empty universe" with ${\langle \rho \rangle }_R=0$ naturally results for universes with a pervasive scale-invariant mass structuring as indicated by the observed two-point correlation functions describing stellar or galactic positions (Bahcall et al., 1988). For such universes we can show that the average mass density ${\rho }_R$ only is finite for a positively curved universe with$k=+1,$ while for universes with $k=0$ or $k=-1$ the mass density vanishes , i.e.${\langle \rho \rangle }_R=0!.$ These latter universes would be "coasting ones" and thus would, as pointed out by Cassado²⁵ explain the distances of supernovae of type SN-Ia without any need for a vacuum energy $\text{Λ}.$

The result for the stellar density distribution in a hierarchically structured universe has an interesting consequence for the night-sky luminosity which we want to mention here: If we may assume here that this form of a stellar or galactic clustering continues to larger and larger cosmic distances (i.e.: scale-invariant clustering!), then this fact perhaps could give an evident solution of the Olbers paradox,⁴¹ namely the fact that the sky during night is dark. Several other possible solutions meanwhile have been offered, all perhaps worth a discussion, but none convincing up to the present, only one has been overlooked up to now. Because under these above mentioned conditions of a scale-invariant stellar clustering one would simply obtain the following growth $O\left(l_{\infty }\right)$ of the illuminated part of the sky in any arbitrary direction with a view cone of$d^2\text{Ω}:$                     

$O\left(l_{\infty }\right)=\frac{1}{l_{\infty }^2{d}^2\Omega }{\displaystyle \underset{l_0}{\overset{l\infty }{\int }}{l}^2}{d}^2\Omega \xi \left(l\right)\frac{\pi r_s^2}{l^2}dl=$

$\frac{1}{l_{\infty }^2}{\displaystyle \underset{l_0}{\overset{l\infty }{\int }}{l}^2}. \xi \left(l\right)\frac{\pi r_s^2}{l^2}dl==\frac{\pi r_s^2}{l_0^2}{\xi }_0. l_0^{\alpha }{\displaystyle \underset{l0}{\overset{l\infty }{\int }}\frac{1}{l^{\alpha }}}dl$

$=\pi r_s^2{\xi }_0{l}_0^{\alpha -2}\frac{l_0^{1-\alpha }}{1-\alpha }[{(\frac{l_{\infty }}{l_0})}^{1-\alpha }-1]$                            (47)

with $r_s$ the standard radius of a standard light candle. First here one can see that for $\alpha =0$ (i.e. no structuring; homogeneous matter distribution!) one would have the following result

$O\left(l_{\infty }\right)=\pi r_s^2{\xi }_0{l}_0^{-1}\left[\left(\frac{l_{\infty }}{l_0}\right)-1\right]$                  (48)

clearly showing that for increasing values of $\left(l_{\infty }/l_0\right)$ the sky coverage would grow to $O\left(l_{\infty }\right)>1$ (i.e. illuminated sky =Olbers paradox!). To the contrast, however, for values as observationally confirmed, namely$=1.8$ , one can see that $O\left(l_{\infty }\right)$ always leads to values $O\left(l_{\infty }\right)<1$ (i.e. non-illuminated sky = no Olbers paradox!).⁴³

None.

The author declares there is no conflict of interest.

1. Friedmann A. Über die Krümmung des Raumes. Zeitschrift f Physik. 1992;10:377.
2. Friedmann A. Über die Möglichkeit einer Welt mit konstanter negative Krümmung. Zeitschrift f Physik. 1924;21:326.
3. Einstein A. Die Feldgleichungen der Gravitation. Sitzungsber. d. Preuss. Akad. Wissensch. 1915;48:844.
4. Einstein A. Kosmologische Betrachtungen der allgemeinen Relativitätstheorie. Sitzungsber. Preuss. Akademie Wissenschaft. 1917;55:142.
5. Perlmutter S. Discovery of a Supernova Explosion at Half the Age of the Universe and its Cosmological Implications. NATURE. 1998;391, 51.
6. Riess AG. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron J. 1998;116(3):1009.
7. Riess AG. Cosmological Acceleration through Transition to Constant Scalar Curvature. Astrophys J. 2001;560:49.
8. Schmidt BP. The high-z supernova search; measuring cosmic deceleration and global curvature of the universe using type Ia supernovae. Astrophys J. 1998;507(1):46.
9. Tonry JL. Cosmological results from high-z supernovae. Astrophys J. 2003;594(1):1.
10. Wang L. Cosmological Applications of a Geometrical Interpretation of “c”. Astrophys J. 2003;590:944.
11. Kang Y. Early type host galaxies of Type Ia supernovae: Evidence for luminosity evolution in supernova cosmology. arXiv: 1912. 04903v2. 2020.
12. Tinsley BM. Evolution of the Stars and Gas in Galaxies. ApJ. 1968;151: 547.
13. Perlmutter S. Supernova cosmology project. Astrophys J. 1997;483:565.
14. Riess AG, Strolger LG, Casertano S. New Hubble space telescope discoveries of Type Ia supernovae at z > 1: narrowing constraints on the early behaviour of dark energy. Astrophys. J. 2007;659(1):98.
15. Dev A, Sethi M, Lohiya D. Linear coasting in cosmology and SNe Ia luminosities. Phys Lett B. 2001;504(3):207.
16. Gehlaut S, Kumar P, Lohiya D. A concordant "freely coasting cosmology". astro-ph/0306448. 2003.
17. Sethi G, Dev A, Jain D. Cosmological constraints on a power-law universe. Phys Lett B. 2005;624(3–4):135.
18. Wei JJ, Melia F, Maier RS. A comprehensive analysis of the supernova legacy survey sample with LCDM- and R=ct –universe. Astron J. 2015;149(3):102.
19. Perlmutter S. Supernovae, Dark Energy, and the accelerating universe. Physics Today. 2003;56(4):53.
20. Kolb EW. A coasting cosmology. Astrophys J. 1989;344:543.
21. Fahr HJ. Cosmological consequences of scale-related comoving masses for cosmic pressure, mass and vacuum energy density. Found Phys Lett. 2006;19(5):423.
22. Fahr HJ, Heyl M. About universes with scale-related total masses and their abolition of presently outstanding cosmological problems. Astronom Nachrichten / AN. 2007;328(2):192.
23. Overduin JM, Copperstock FI. Evolution of the scale factor with a varaibel cosmological term. Phys Rev D. 1998;58(4):043506.
24. Fahr HJ, Zoennchen J. Cosmological implications of the Machian principle. Naturwissenschaften. 2006;93:577.
25. Casado J. Linear expansion models vs. standard cosmologies: a critical and historical overview. Astrophys Space Sci. 2020;365:16.
26. Casado J. Modelling the expansion of the universe by a steady flow of space time. APEIRON. 2009;16(2):161.
27. Casado J, Jou D. Steady flow cosmological model. Astrophys Space Sci. 2013;344(2):513.
28. Bahcall NA. Large scale structure in the universe indicated by galaxy clusters. Ann Rev Astron Astrophys. 1988;26:631.
29. Bahcall NA, Chokski A. The clustering of radiogalaxies. Ap J. 1992;385:L33.
30. Sylos-Labini F, Vasilyev NL. Absence of self-averaging and of homogeneity in the large scalegalaxy distribution. Astron Astrophys. 2008;477:381.
31. Sylos-Labini F. Gravitational fluctuations of the galaxy distribution. Astron Astrophys. 2010;523:A68.
32. Fahr HJ, Heyl M. Stellar matter distribution with scale-invariant hierarchical structuring. Phys Astron Int J. 2019;3(4):146–150.
33. Goenner H. Einführung in die Kosmologie. Spektrum Verlag. 1994.
34. Fliessbach T. Allgemeine Relativitätstheorie. Wissenschaftsverlag BI, Mannheim/Wien/Zürich. 1990.
35. Benett CL. First-Year Wilkinson Microwave Anisotropy Probe (WMAP)1 Observations: Foreground Emission. Astrophys J Suppl Ser. 2003;148:97.
36. Buchert T. On average properties of inhomogeneous fluids in general relativity. General Relativity and Gravitation. 2001;33(8):1381.
37. Buchert T. A cosmic equation of state for a inhomogeneous universe: can a global far from equilibrium state explain dark energy?. Classical and Quantum Gravity. 2005;22(19):L113.
38. Wiltshire DL. Cosmic clocks, cosmic variance and cosmic averages. New Journal of Physics. 2007;9:377.
39. Goenner H. Einführung in die Spezielle und Allgemeine Reltivitätstheorie. Spektrum Akad. Verlag, Heidelberg-Berlin-Oxford. 1996.
40. Thirring H. Über die Wirkung rotierender ferner Massen in der Einstein‘schen Gravitationstheorie. Phys Z. 1918;19:33.
41. Soergel-Fabricius C. Thirring Effekt im Einstein Kosmos. Zeitschrift f Physik. 1960;159:541.
42. Olbers HWM. Über die Durchsichtigkeit des Weltraums. Astronomisches Jahrbuch für das Jahr 1826, Berlin. 1926;1823:110.
43. Casado J. A steady flow cosmological model from a minimal large numbers hypothesis. APEIRON. 2011;18(3):297.