The paper presents a hybrid model of constituent quark which considers the preonic structure based on $z^0$ (34 m_e)-preon, specific to the previously published cold genesis theory (CGT) of the author and basic concepts of the S.M. which seem experimentally sustained, explaining the constituent quarks forming from current quarks and “gammonic” gluols –in concordance with the experimentally evidenced possibility of paired quarks forming from relativist jets of negatrons and positrons, by considering that the negatrons and positrons can form ‘gammonic’ “gluols” and thereafter- current and constituent quarks, by the magnetic and electric interactions between the paired quasielectrons (degenerate electrons),  which can explain the constituent u- quark’s stability until the critical temperature 2x10¹² K, without the concepts of “color charge” and of “virtual” gluon/boson.

The resulted hybrid model can also explain why in strong interactions the sum rule can be applied correspondent with the transferring of some quarks from an interacting particle to another  with the entire or almost entire their constituent mass. Also, it suggests that the mechanism of paired current u-quarks forming from gluons, used by the S. M., can be plausible in conformity with the mass conservation law only if the quantum vacuum contains real thermalized “gammons” considered as (e⁺e^-)^*-pairs of degenerate electrons.

Keywords: quark model, strong interaction, preons, cold genesis, nucleon structure, gluon.

In the Standard Model, it is known the constituent quark model with a valence quark (u, d, s, c, b, t) having a current mass:¹ ((1.8¸2.8; 4.3¸5.2; 92¸104) MeV/c²; (1.3; 4.2¸4.7; 156¸176) GeV/c²) and a gluonic shell formed by gluons and  sea-quarks,¹ the resulted effective quark mass being the constituent quark mass: (336, 340, 486) MeV/c², respective: (1.55, 4.73, 177) GeV/c².  The electric charge of u-, c-, t- quarks is $+\left({}^2{/}_3\right)e$  and the electric charge of d-, s-, b- quarks is $–\left({}^1{/}_3\right)e$ , the strong interaction of quarks being explained by so-named “color charge”,  the gluons having two opposed color charges, the gluon field between a pair of color charges forming a narrow flux tube (as a ‘string’) between them, the Lund string model² indicating that "strings" of low-energy gluons can be formed most strongly between the quarks, the strong force between quarks resulting as constant regardless of their separation.

Conform to the S.M., at the high-energy gluons the "breaking" of these strings into new quark–antiquark pairs can occurs, as part of the hadronization process. It is also considered that the gluons can acquire rest mass by the Higgs mechanism, of coupling to the Higgs field, the upper limit for the gluon’s mass experimentally determined being 1¸1.3 MeV/c².³ Also, the S.M. considers approximately the same size order for the maximum radius of the electron, resulted as scattering center determined inside the electron with X-rays: $~{10}^{-18}m$ ⁴ with that of the scattering centers experimentally determined inside the  nucleon: 0.43x10^-18 m,⁵ considered as quarks in the S.M. The possibility of quark-antiquark –pairs obtaining by the interaction of relativist fluxes of negatrons and positrons is explained in the S.M. by the conclusion of e⁺ -e^- annihilation, with paired quarks forming from a high energy photon, resulting by the energy of the collided electrons.

However, in a quark model of a Cold Genesis Theory (CGT),^6-8 resulted as cluster of degenerate electrons e^*, these scattering centers of $~$ 10^-18 m are considered  electronic super-dense centroids, the generating of heavy quarks and of heavy particles being explained using the known quark s(~500 MeV) and two semi-light quarks:${\lambda }^{\pm }\left(435MeV\right)$ and $v^{\pm }(~574MeV)$ specific to astro-particles’ forming, in CGT, the masses of the quarks $c^{•}$ (charm) and $b^{•}$ (bottom) of the Standard Model but also the values  used by de Souza:⁹ c = 1.7 GeV and b = 5 GeV, being re-obtained as tri-quark clusters in the form: [(q q* )q], (q*-anti-quark), by a simple de-excitation reaction, with the emission of a preonic boson obtained in CGT: $z^0=34m_e$ , respective:$z_2=4z^0$ and $z_m=6z^0$ - for  the quarks and b, a similar  de-excitation reaction, with the emission of a preonic boson $z_k=n\times z^0$ , (n = 1¸7) representing less than 2.7% from the particle’s mass, explaining the experimentally obtained masses of heavy baryons and of some heavy mesons.

The value $m\left(z^0\right)=34m_e$ of the basic preon’s mass corresponds to that of the boson X(17) experimentally evidenced in 2015¹⁰ by a reaction:

$Li7+p^{+}\to Be*\to Be8+X\left(17\right); X\left(17\right)\to e^{+}+e^{-},$  (1)

and reconfirmed in  2019 [11] , but predicted by CGT in 2006.⁶

Conform to the model,^6-8 the heavy current quarks results by lighter current quarks with quasi-crystalline internal structure, by an arrangement with trigonal/hexagonal symmetry of preonic kernels, by two preonic bosons: $z_2=4z^0$ ; $z_{\pi }=7z^0$ , the top-quark resulting as: $t=17(b\overline{b})+b=\left(7x5\right)\cdot m\left(b\right)$ , with a kernel of regular hexagonal polyhedron form, given by kernels of  b-quarks.⁸

The electron’s magnetic moment results in CGT as vortex ${\Gamma }_{\mu }$ of ‘quantons’, with mass $m_h=h\cdot 1/c^2$ , the nuclear potential being obtained by the superposition of the $\left(N^p+1\right)$ quantonic vortices, ${\Gamma }_{\mu }{}^{*}$ , of the protonic quasielectrons (degenerate electrons, with reduced mass: $m_e{}^{*}=0.809m_e$ (giving $N^p=2268$ ) and diminished magnetic moment ${\mu }_e{}^{*}$ , which generates inside a volume with radius:$r_{\mu }{}^a\approx 2$ fm, a total dynamic pressure:$P_n=\left({}^1{/}_2\right){\rho }_n\left(r\right)\cdot c^2$ which gives an exponential nuclear potential:

$V_n\left(r\right)=-{\upsilon }_i{P}_n\left(r\right)=V_{n0}\cdot e^{-r/}{}^{\eta *}$ ;  
$V_{n0}=-u_i{P}_n{}^0=-({\upsilon }_i{/}_2){\rho }_n\left(r\right)\cdot c^2$   (2)

 of Eulerian form, with:$\eta *=0.8fm$ and ${\upsilon }_i$ (0.6fm)- the ‘impenetrable’ volume.^6,7

 The decreasing of the particle’s magnetic moment with the particle’s mass is explained in CGT by the conclusion that the ${\Gamma }_{\mu }{}^e$ – vortex of the magnetic moment of an attached positron (which gives the proton’s charge), is diminished by the distribution of its vortical energy to all degenerate electrons of the particle’s $N^p$ –cluster of ‘gammons’, giving the particle’s magnetic moment by an un-paired quantonic vortex of radius $r_{\mu }{}^p$ equal to the reduced Compton wavelength and of circulation:

${\Gamma }_{\mu }^p=\text{2}\pi \text{c}\cdot {\text{r}}_{\mu }^{\text{p}}={\text{ g}}_{\text{p}}\frac{{\text{m}}_{\text{e}}}{{\text{m}}_{\text{p}}}{\Gamma }_{\mu }^{\text{e}}\text{ , }\Rightarrow {\text{ r}}_{\mu }^{\text{p}}={\text{ g}}_{\text{p}}\frac{{\text{m}}_{\text{e}}}{{\text{m}}_{\text{p}}}{\text{ r}}_{\mu }^{\text{e}}{\text{ ; (r}}_{\mu }^{\text{e}}=\frac{\hslash }{{\text{m}}_{\text{e}}\text{c}}\text{); }{\mu }_{\text{p}}=\frac{\text{1}}{\text{2}}{\text{ ecr}}_{\mu }^{\text{p}}={\text{g}}_{\text{p}}\frac{{\text{m}}_{\text{e}}}{{\text{m}}_{\text{p}}}{\mu }_e$   (3)

with the value of g_p  given by the local density of proton’s volume in which the protonic positron’s centroid is found,⁶ (g_p=2.79 - for proton).

A small impenetrable quantum volume u_I is considered in CGT not only for nucleons and quarks, but also for the vector photon, for electron- (resulted with classic radius a = 1.41 fm, corresponding to e-charge in its surface)  and for the $z^0$ –preon, this kernel  resulting with  a radius:$r_{iz}=3x{10}^{-2}$ fm –for the free electron, respective:  3.5x10^-2 fm for the $z^0$ - preon,⁶ which- in this case, has a similar shell, of photons with rest mass (CGT),^6-8 transmitted to the formed quark.  The conclusion of a photon’s rest mass comparable with their  relativist mass was argued by the Galilean relativity and the d’Alembert paradoxe¹² and is in concordance with the possibility to obtain a B-E condensate of photons.

The neutron results in CGT conforming to a Lenard-Radulescu dynamid model, as being composed by a protonic center and a negatron revolving around it with the speed $v_e{}^{*}<<c$ , at a distance $r_e{}^{*}\approx 1.36$ fm,⁶ (close to the value of $\text{~}$ 1.25 fm used by the equation of empirical nuclear radius:$R_n\approx r_0\cdot A^{1/3}),$ at which it has a degenerate ${\mu }_e{}^S$ magnetic moment and $S_e{}^n$ -spin.

The weak force of beta-emission is explained by the disintegration of a linking “gammon” formed as pair of magnetically coupled quasielectrons:${\gamma }^{*}\left(e^{*-}{e}^{*+}\right)$ whose superdense centroids give the electronic antineutrino, (the photonic shell being transformed into disintegration energy ${\in }_d$ ), the couple:$w^{-}(e^{-}{\gamma }^{*})$ forming a “weson” which added to the u-quark gives the d-quark.

The neutron’s disintegration is explained as a reaction of d-quark’s transforming, in the form:

$d^{-}\to u^{+}+e^{-}+{\overline{\nu }}_e +{\in }_{d }$ ;$(w^{-}(e^{-}{\gamma }^{*})\to e^{-}+{\overline{\nu }}_e+{\in }_d)$ (4)

Also, the nucleonic quarks u⁺, d^-, with constituent mass of (312, 313) MeV/c², results from light mesonic quarks:  $m_1{}^{+};m_2{}^{-}=m_1{}^{+}+w^{-}$ , $m_1{}^{+}$ -quark (‘mark₁’) resulting  from the preonic boson z₂(69.5MeV) by the loosing of a quasielectron e^*-, (Figure 1&2).

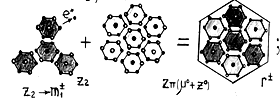
Figure 1 The $m_1{{}^{*}}_{,}{z}_{\pi }{}^{*}$ and $r^{*}$ - quark pre-clusters forming from $z^0$ -preons.

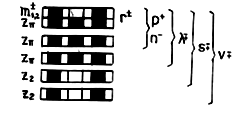
Figure 2 The semi-light cold forming of quarks by pre-clusters of $m_{1,2}$ ;$z_2$ and $z_{\pi }$ .

A main difference between the quark model of S.M. and that of CGT is given by the fact that in the S.M. the nucleon’s current quarks are considered without sub-structure and with a “color” charge of strong interaction, not satisfactory explained- from phenomenological point of view. Also, conform to CGT, the preonic clusters retain (also at their releasing), by their vortical field (given by superposed ${\Gamma }_{\mu }{}^{*}$ -vortices of degenerate electrons’ magnetic moments),⁶ a photonic shell of mass proportional with the number of  kernels of quasielectrons which compose the preonic boson’s kernel, (i-e- corresponding to the boson’s effective mass), in accordance with the  next equations of the electron’s intrinsic rest energy, used in CGT:⁶

$m_e{c}^2\approx \mathrm{½}{{\displaystyle \int \epsilon }}_0{E}^{2}dV\left(r\right) \approx \mathrm{½}{\displaystyle \int {\mu }_0}{H}^{2}dV\left(r\right);$   (5)

$E=cB;$ $(r=0÷r_{\mu }=ħ/m_{e}c)$   

that explains the electron’s mass m_e as saturation value: n×m of magnetically (vortically) confined ‘naked’ photons. These ${\Gamma }_{\mu }{}^e$ -vortices are maintained by the negentropy of the quantum vacuum given by etherono-quantonic winds (fluxes) which explains also the constancy of the magnetic moment of the free charged particles, in CGT.⁶

Compared to CGT, which is based to the sum rule (mass-energy conservation law) and to the Galilean relativity, the S.M. does not explain how in a strong interaction a current quark of a particle can transfer to the interaction partner the same constituent mass (carrying only its gluonic shell). The aim of the paper is to explain this fact by a toy quark model, resulted as hybridization between the quark model used in Quantum Chromodynamics and those used in CGT.

Hybrid model of constituent quark

The model of light/semi-light quarks

For a hybrid model of quark with  concordance  with experimental data, but more natural than that of the S.M., we will identify the quark’s current mass with the quark’s kerneloid resulted in  CGT⁸ with a radius $r_q\le 0.3fm$ –conformed to some previous experiments,¹³ and the quark’s constituent mass given by addition of $z_2$ – and $z_{\pi }$ - bosons formed by $z^0$ –preons, as in CGT, (Figure 1&2), but considering- as in the S.M. (in a simplified way, corresponding to a “toy” model) that the entire mass of the current quark is contained in its (kerneloidic) volume $${\upsilon }_q\left(r_q\right)$$ and that the entire mass of the $z^0$ –preons is contained by their sub-components.

In this case, for simplify the model in relative concordance with the S.M., we consider conventionally, for a first analyse, that the entire mass of a quasielectron is contained in an electronic kerneloid ${\upsilon }_e\left(r_e{}^{*}\right)$ of radius $r_e{}^{*}\approx 0.01÷0.025fm$ , (the value $r_e{}^{*}\approx 0.01fm$ representing the electron’s mechanical radius resulted from some high-energy scattering experiments reported by Milonni et al.),¹⁴ whose mass is given by inertial masses of heavy photons.

We observe also that the linking “gammon” considered in CGT, of mass: $m_{\gamma }({\gamma }^{*})=2x{m}_e{}^{*}=0.827$ $MeV/c^2<1.3MeV/c^2$ , can be  considered a neutral “gluol”, g_l,  i.e.- the equivalent of a gluon considered by the S.M., with conventional spin ±1 but with natural rest-mass, (resulted by inertial masses of “frozen” photons, of radius $r_f \le {10}^{-18}m$ – in accordance with a classic model of electron based on the Galilean relativity).^7,8 The mass-energy difference $\delta m_e{c}^2=\left(m_e–m_e{}^{*}\right)c^2\approx 0.19m_e{c}^2$ can be interpreted as equal with the binding energy per quasielectron.

Figure 3 The $z^0$ -preon forming from gluols in variant a), b) and paired current u-quarks forming, c)

 For develop the proposed quark hybrid model by the approximation of the sum rule, we must define the current u-quark (current p-quark –in CGT) and the z⁰-preon by the previous assumptions, considering only the quasielectrons as the most basic components, with degenerate mass:

$m_e{}^{*}=0.8095m_e$ and charge $e^{*}{}^{\pm }=\pm \left({}^2{/}_3\right)e$ - specific to a quark model of quasielectrons cluster type.

First, we observe that a cluster formed by a quasielectron $e^{*}{}^{\pm }$ surrounded by three magnetically and electrically coupled gluols can be identified with a current u/u^*-quark, with approximate mass:

$u^{+}=(e^{*}{}^{\pm }+3g_l)$   ; $m_o(u^{\pm })=m(e^{*}{}^{\pm }+3g_l)=7m_e{}^{*}=2.895MeV/c^2$ ,  (6)

(the variant u^- being an u^*-antiquark, with negative $-\left({}^2{/}_3\right)$ e-charge). 

The current d-quark, with electric charge ${-}^1{/}_3)$ e, results in this case conform to eq. (4), as: 

$d^{-}=u^{+}+w^{-}=(e^{*}{}^{\pm }+3g_l)+g_l+e^{-}$   ;
$m_0(d^{\pm })=m(9e^{*}{}^{\pm }+e^{-})= 4.23MeV/c^2$   (7)

It is observed that the resulted current masses for u- and d- quarks correspond to the upper limit, respective- to the lower limit  considered by the S.M. , (2.8 MeV/c², respective- 4.3 MeV/c²).

For the obtaining of their constituent masses by the sum rule, is useful to use the quasicrystalline model of constituent quark resulted in CGT as formed by a ‘mark’-quark (m₁⁺; m₂^-) with addition of a preonic boson:$z_6=2z_{\pi }$

For this purpose, considering the pair $(u\overline{u})$ as neutral “pison”, $d_{\pi }{}^0$ , (pionic boson), and the cluster $u^0\left(3g_l\right)$ as neutral $u^0$ -pseudo-quark we observe that the value $m\left(z^0\right)=42m_e{}^{*}=34m_e=17.37MeV/c^2$ can result by  two variants of the $z^0$ –preon’s forming, (Figures 3a &3b):

1. $z^0=7\left(3g_l\right)=7u^0; \Rightarrow m\left(z^0\right)=21xm\left(gl\right)$ ;
2. $z^0=3(u\overline{u}) =3d_p{}^0; \Rightarrow m\left(z^0\right)=6xm\left(u\right)$   

$\left(m\left(z^0\right) =17.37MeV/c^2\right)$   ;

In both cases, the (cold) form of $z^0$ –preon results as hexagonal, (Figures 3a &3b) and corresponds to the possibility of ‘splitting’ into a pair of current ‘quarcins’:$c^{\pm }=\left({}^1{/}_2\right)z^0$ by the splitting of a $(u\overline{u})$ -pair or- respectively, of a g_l –gluol, in concordance with eq. (1), i.e.:

1. $z^0\left[7u^0\right]\to c^{+}\left[3u^0+g_l+e^{*+}\right]+c^{-}\left[3u^0+g_l+e^{*-}\right]$   (8a)                                 

         or:  

2. $z^0[3(u\overline{u})]\to c^{+}[d_{\pi }{}^0+u\left]+c^{-}\right[d_{\pi }{}^0+\overline{u}]$   

The light m₁ –quark or m₂ -quark results in this case by the transforming of a $z^0$ –preon into a z⁺- or z^-- pre-quark by acquiring of a quasielectron $e^{*+}$ or of a couple:$\left(e^{*+}+w^{-}\right)$ in the middle of the central $u^0$ -pseudo-quark –in the variant a), (Figure 4a), or by the acquiring of a current u -quark or d-quark in the middle of the $z^0$ –preon – in the variant b), (Figure 4b), resulting a valence pre-quark $z^{\pm }$ which attracts magnetically current $u^0$ -pseudo-quarks of a number of three $z^0$ -preons (in variant a)) or magnetically current u –quarks and electrically current $\overline{u}$ anti-quarks of a number of three $z^0$ -preons (in variant b)), resulting the quasi-crystalline (quasi-stable) form of the constituent m₁- ; m₂ – quark, (as in Figure 1).

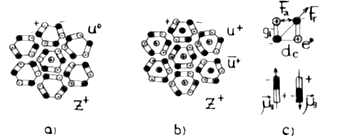
Figure 4 The z+-pre-quark forming from gluols in variant a), b) and a pair of gluols forming c)

The most natural variant, concordant with the possibility to explain the proton’s mass and the neutron’s mass with discrepancy under 1% by the value:$m_e{}^{*}\approx 0.8095$ obtained in CGT, is the variant a). For this case, the current $u^0$ -pseudo-quarks are the equivalent of the “virtual quarks” of the “quarks-sea”, considered by the S. M. However, the variant b), for concordance with the proton’s mass imply the recalibration of the masses of the proton’s sub-components, resulting:

$-m\left(u\right)=938.24/\left(54x6+1\right)=2.887MeV/c^2$ ; 

$-m_e{}^{*}=m\left(u\right)/7=0.807m_e$ ; 

$-m\left(d\right)=m\left(u^{+}+w^{-}\right)=4.\left(2\right)MeV/c^2$ ;

$-m\left(z_0\right)=6m\left(u\right)=17.32MeV/c^2$  .

But because the resulted values are close enough, we can choose either b)- variant or a)- variant.

Also, because the quarks are charged components, it seems that the concept of ‘sea-quarks” used by the S.M. for explain the shell of the current quark is more compatible with the explanatory variant b) by considering the current quark’s shell as formed by “pisons” $d_{\pi }{}^0(u\overline{u})$ forming $z^0$ –preons arranged in superposed layers of $z_2\left(4z^0\right)$ and $z_{\pi }\left(7z^0\right)$ , as in CGT, with the quasi-crystalline structure of the constituent quarks obtained also by CGT, as in Figure 2.

By eq. (2), the resulted hybrid model can explain the nuclear and the strong interactions between current quarks. The reactions of strong interaction in which preonic z_k- bosons and bosonic pairs $(q-\overline{q})$ can be formed from “gammonic” g_l -gluols of the quantum vacuum, with total mass $M\approx Q/c^2$ , (Q- the interaction energy), are explained by the conclusion that the preonic bosons formed by magnetic interactions between g_l -gluols may generate heavier quarks in combination with the initial quarks, such as in the interaction:

(Experimental reaction): ${\pi }^{-}({\overline{m}}_1+m_2)+p_r\left(2p^{+}+n^{-}\right)+Q\to {\Lambda }^o\left(s+n+p\right)+K^o(m_2+\overline{\lambda })$ ;  

${\pi }^{-}({\overline{m}}_1+m_2)+p_r\left(2p^{+}+n^{-}\right)+Q\to {\Lambda }^o\left(s+n+p\right)+K^o(m_2+\overline{\lambda })$ ;  (9)

$s^{-}+n^{-}+p^{+}\to {\Lambda }^o$ ; $\overline{\lambda }+m_2\to K^o$ ; - permitted reaction; ($z_2=136m_e$ ; $z_6=2z_{\pi }= 476m_e$ ).

The transferring of the entire constituent mass of a quark from a high speed particle to its interaction partner can be explained in this case by the approximation of the sum’s rule. Because the quarks’ maintaining inside the nucleon (inside the particle’s volume, generally) can be explained satisfactory without the concept of “color charge”, and because the most basic sub-structure necessary to explain the quark’s masses are the “gammonic” gluols $g_l\left(e^{*+}{e}^{*-}\right)$ resulted as pairs of degenerate electrons, the quarks’ forming from relativist jets of negatrons and positrons, experimentally observed,¹⁵ can be explained more naturally than in the case of the S.M. which deduces the  paired quarks forming from gamma –quantum of high energy but which cannot explain the selection rule for the masses of the resulted quarks without the concept of “Higgs field”.

The heavy quarks

The constituent masses of the heavier quarks (charm or “chark”) and b (bottom or “bark”) in the Souza/CGT mass variant:$m\left(c\right)\approx 1.7GeV$ and $m\left(b\right)\approx 5GeV$ , results as triplets of less heavy quarks by the aid of the Carrigan’s formula,¹⁶ conform to a  (semi)empiric equation⁸ the quarcic cluster q^c_k:⁸

$m\left(q_n{}^c\right)=3^{n-1}\left[m_1–\left(z^0/3\right)ln\left(3^{n-1}{3}^{n-2}\right)\right]; n>1$  (10)

with:$m_1=m\left(v^{-}\right)=0.574GeV/c^2$  $z^0=34m_e$ ;  and $ln\left(3^{n-1}{3}^{n-2}\right)=ln{3}^{2n-3}$ , which gives:

$-n=2\to m\left(q_2{}^c\right)c^2=1.703GeV$ ;

$-n=3\to m\left(q_3{}^c\right)c^2=4.994GeV$  ;

$-n=4\to m\left(q_4{}^c\right)c^2=14.64GeV$ .
By considering formally the energy: $\Delta E_q=m({\delta }_k)c^2$ , loosen at the de-exciting of the quarcic cluster $q^c{}_n$ , as binding energy between quarks, (by similitude with a nucleus),  the logarithmic part of the second term of the expression (10) indicates that the considered binding energy per v-quark increases with the number of v-quarks.  

A relative similar semi-empiric relation may be found also for the quarks $c^{•}\approx 1.55GeV$ and $b^{•}\approx 4.73GeV$ , of the S.M., but in the form:

$m(q_n{}^{•})=3^{n-1}[(m_1{}^{•}+{\delta }^{·}{}^{•})+\left(z^0/3\right)ln{3}^{n-2}], n>1$ ;   (11)
$(m_1{}^{·}+{\delta }^{·}{}^{·}) =\left(2m_s+m_v–z^0\right)/3$        

with: $m_1{}^{·}=m_s\approx 500MeV/c^2,\Rightarrow {\delta }^{·}=19MeV/c^2$ , (or:$m_1{}^{·}=m_s{}^{·}\approx 486MeV/c^2,\Rightarrow {\delta }^{·}=33MeV/c^2$   ), giving:$-n=2\to m(q_2{}^{·})c^2=1.557GeV\approx m(c^{·})$   ; 

$-n=3\to m(q_3{}^{·})c^2=4.728GeV$ .

   The expression (11) is characteristic to mass addition to the tri-quark cluster, (as consequence of the fact that was taken: $m_1{}^{·}=m_s$ instead of: $\left(2m_s+m_v\right)/3)$ , as in the case of the Sakharov’s equation,¹⁷ (which adds a term of spin-spin interaction at the total mass of quarks)  and shows a link between the masses of $s-,c^{·}-,b^{·}-$ quarks and $z^0\left(34m_e\right)$ .

The mass variant used by the S.M. of the quarks $s^{·}\left(486\right) c^{·}\left(1550\right);b^{·}\left(4730\right)$ results from the CGT’s quarks:$s^{-},c^{+},b^{-}$   in Souza/CGT mass variant by the approximate reactions:     

$- c\left(1700\right)\to c^{·}\left(1560\right)+{\pi }^0\left(2z_2\right);$  

$-b\left(5000\right)\to b^{·}\left(4756\right)+z_6(2z_{\pi });$   (12)

$- s^{\pm }\left(500\right)\to s^{·}{}^{\pm }\left(483\right)+z^0$ .

The reactions (12) correspond to the ‘hot’ forming of S.M.’s quark at high values of interaction energy, from metastable (non-de-excited) quark:$s^{-},c^{+},b^{-}$ . Also, in concordance with eq. (1) it results:

$v\to v^{·}+z^0.$  

The paired current quarks generating from ‘gluols’

According to the sum’ rule, the gluon’s transforming into a pair of current u-, d- quarks seems not possible if the effective mass of the gluon is lower than that of the current quark. However, the current u-quark model and the ‘gluol’ model used in the proposed constituent quark hybrid model permit the next mechanism of the paired current u-quarks forming by the gluol’s splitting;

-Supposing that the vibration of the paired quasielectrons of a gluol attains a critical amplitude $A_v\approx 1$ fm, at this interdistance  the quasielectrons can attract polarized quasi-free gluols attracted by the particle’s vortical field inside its quantum volume (by a potential of the form (2) resulted as sum of the $V_n\left(r\right)$ -potentials generated by the rest part of the quasielectrons by the quantonic vortices ${\Gamma }_{\mu }{}^{*}$ ),^6,7 the remained three gluols per separated quasielectron forming with this quasielectron a current u-quark (respective-antiquark) which thereafter can be transformed into current d-quark (or antiquark), conform to the proposed “toy” model, (Figure 3c).

This model corresponds to the Quantum mechanics’ conclusion that there are many e⁺e⁻ pairs in the quantum vacuum and these pairs tend to be in the configuration where the opposite charge of the pair is closer to the observed electron, the quantum vacuum near the electron being polarized, (lowering the observed charge of the electron).  The process is therefore similar to that of the water droplets forming from steam with ions at the temperature’s lowering. Similarly, it results that the current quark’s forming from electrons and ‘gluols’ is impeded by a high temperature of the gluols gas and a high electron’s speed and is favored by a lower temperature and a high density n of the gluols gas (and by a low electron’s speed), conform to the known formula of the Bose-Einstein condensate’ forming: $T_{BE}=3.3125x({ħ}^2{n}^{2/3})/k_b\cdot m$   ,

 (m- the gluol’s mass- in this case).

The ‘gluols’ of the model are –in this case, equivalent to the virtual charge pairs of the quantum vacuum but as real ‘un-matter’ quanta, (pairs of matter-antimatter type). The paired current u-quarks forming from relativist jets of negatrons and positrons can be explained –in this case, by the forming of ‘gammonic’/gluonic pairs in the impact zone with the increasing of the density of gluols gas and by gluols attraction by slowed electrons resulted from pseudo-plastic e⁺ -e^- -interactions, conform to the model.

The magneto-electric attraction between quarks in a ‘toy’ model of interaction

From Figures 3&4, we observe that the minimal radius of a current u-quark, corresponding to the “cold” quark (with intrinsic temperature $T_i\to 0K$ ) is approximate equal to: $r_q{}^m\approx 3r_e{}^{*}=0.03fm$ , ($r_e{}^{*}\approx 0.01$ fm –the electron’s radius reported by Milloni),¹⁴ the maximal value r_q^M corresponding to the excited quark ($T_i>>0K$ ) being approximated by considering that the proton’s mass is extended until the surface of its volume considered with a mean radius $r_p\approx 0.85fm$ ,¹⁸ resulting from figure 4 that : r_q^M » r_p/9 = 0.094 fm, ($\approx 0.1fm$ ), corresponding to a mean interdistance between paired quasielectrons of value: $d_e{}^M\approx \left({}^2{/}_3\right)r_q{}^M\approx 0.062fm$ .

The possibility to explain the quarks’ retaining into the nucleon’s volume by a classic “bag” model is presented in Ref.¹⁹ But we observe that an important force which can explain the proton’s stability is given by the magneto-electric interaction between the adjacent degenerate quasielectrons of adjacent current quarks. For example, the value of the interaction potential between an electron and a positron of a 1MeV-gamma quantum, corresponding to a separation energy of the same value, can be explained as sum of the electrostatic energy and the magnetic energy of the (e+- e-) pair, i.e:

$E\gamma =2m_e{c}^2=V_e\left(d_i\right)+V_{\mu }\left(d_i\right)=e^2/4\pi {\epsilon }_{0}a;$   (13)

$V_e\left(d_i\right)=e^2/4\pi {\epsilon }_0{d}_i$ ; $V_{\mu }\left(d_i\right)={\mu }_r·B\left(d_i\right)\approx e^2/8\pi {\epsilon }_0·d_i$ ,  

 resulting that: d_i = 1.5a, (a = 1.41fm).

  The expression of $V_{\mu }\left(d_i\right)$ results as consequence of the fact that –under the electron’s Compton radius $r_{\lambda }$ , for $di\le r_{\lambda }=h/2\pi m_{e}c=386fm$ , (defined physically as the value until to the magnetic moment’s quanta have yet the light speed), we have the relation: B = E/c, (characteristic also to the electromagnetic wave), the relative radius $r_{\mu }{}^{*}$ of the relative magnetic moment ${\mu }_r$ of a degenerate electron resulting according to:

$\begin{array}{l}B(d)=\frac{\text{E(d)}}{\text{c}}=\frac{e}{4\pi {\epsilon }_0\cdot d^{2}c}=\frac{{\mu }_0}{2\pi }\frac{{\mu }_{\text{r}}}{{\text{d}}^{\text{3}}}=\frac{{\mu }_0}{2\pi }\frac{e\cdot r_{\mu }^{*}c}{2\cdot d^3},\text{(d}\le {\text{r}}_{\lambda }=\frac{h}{2\pi m_{e}c}\text{) }\\ \Rightarrow {\text{r}}_{\mu }^{\text{*}}=d\text{; }{\mu }_{\text{r}}={\mu }_{\text{e}}(d/{\text{r}}_{\lambda });{\text{ V}}_{\mu }^{\text{r}}={\mu }_r\cdot B_r(d)=e^2/8\pi {\epsilon }_{0}d;{\text{ F}}_{\mu }=-\nabla V_{\mu }^r=e^2/8\pi {\epsilon }_0{d}^2\end{array}$   (14)

Because the increasing of the quantum vacuum’s density inside the elementary particle, (evidenced also by the photon’s slowing at its passing through a Bose-Einstein condensate)²⁰ we can approximate the value of the electric permittivity inside the particle’s volume as being:$\epsilon ={\epsilon }_0{\epsilon }_r\approx 2{\epsilon }_0$ ⁷ and corresponding to a light speed $c’=1/\surd (\epsilon {\mu }_{0 }\approx c/\surd 2$ and to a ratio: $F_{\mu }\left(d\right)/F_e\left(d\right)=1$ , which gives a hexagonal arrangement of the quasielectrons of the current  u- quark (Figure 4b, Figure 5c), the equilibrium radius r₀ of interaction between the central quasielectron and the quasielectrons with antiparallel magnetic moments ${\mu }_r{}^{*}$ and the same electric charge $e^{*}=\left(2/3\right)e$ (or inverse) resulting by the attraction between the “gluolic” quasielectrons on circumferential direction with a force:

$F_t\left(d_c\right)=F_{\mu }\left(d_c\right)+F_e\left(d_c\right)\approx 2F_{\mu }\left(d_c\right)= e^{*2}/4\pi {\epsilon }_0{d}_c{}^2$   (15)

The hexagonal form of the u-quark is explained by the fact that the repulsion force $F_r(d_c)=F_e(d_c)$ between the central quasielectron and a ‘gluolic’ quasielectron is canceled by the attraction force $F_u=-2F_e(d_c)\cdot cos{60}^o=-F_e(d_c)$ of the adjacent quasielectrons of opposed charge (Figure 5c). 

Figure 5 Nucleonic kernel formed by quarks coupled laterally a) and axially b) and the forming of a current $\overline{u}$ -quark c).

The repulsion force acting over a paired quasielectron of a g_l –gluol coupled with another is given by the diametrally opposed quasielectron having an interdistance $d_r=d_c\surd 2$ , (Figure 4c), which gives a total repulsion force:

$F_r(\surd 2d_c)=F_{\mu }(\surd 2d_c)+F_e(\surd 2d_c)\approx F_m\left(d_c\right) =e^{*2}/8\pi {\epsilon }_0{d}_c{}^2$ .

So, the total value of the interaction force between two current quarks is approximately of double value, being given by two pairs of adjacent interacting quasielectrons, (Figure 4c), i.e.:

$F_q\left(d_c\right)\approx 2[F_t\left(d_c\right)–F_r(\surd 2d_c)]=2F_{\mu }\left(d_c\right)$   (16)

$\Rightarrow F_q\left(d_c\right) =e^{*2}/4\pi {\epsilon }_0{d}_c{}^2 =e^2/9\pi {\epsilon }_0·d_c{}^2, \left(e^{*}=\left({}^2{/}_3\right)e\right)$  

For a minimal interdistance $d_c{}^m =2r_e{}^{*}=0.02fm$ , by eq. (16) it results a maximal interaction force between adjacent current u-quarks:

$F_q\left(d_c{}^m\right)\approx 2.5x{10}^5$ N – of 25 times higher than those resulted in Quantum Chromodynamics ($\text{~}$ 10⁴ N).

At the maximal interdistance:$d_c{}^M \approx \left({}^2{/}_3\right)r_q{}^M\approx 0.062fm$ between quasielectrons, it results a mean interaction force between adjacent current u-quarks:$F_q\left(d_c{}^M\right)\approx 2.5x{10}^4$ N –of 2.5 times higher than those resulted in Quantum Chromodynamics.

Mathematically, the explanation of this high value consists in the fact that it was considered a variation with $r^{-2}$ also inside the particle’s volume, similar to the case of “color” charge’s interaction. More realistic would be to consider that – at a normal nuclear temperature $({10}^8÷{10}^{10}K)$ , the constituent quarks have all the valence quarks and $z^0$ - preons inside the nucleon’s impenetrable volume of a radius $r_i\approx 0.6fm$ , (the radius $$r_p=0.85fm$$ $r_p=0.85fm$ corresponding in this case to a dilated (maximally excited) impenetrable volume of $T\approx {10}^{12}K$ ).

The interdistance $d_i$ between the preonic quasielectrons results- in this case, (conform to Figure 4), of value:$d_c{}^i=\left({}^2{/}_3\right)r_i/9=0.0\left(4\right)fm$ and corresponds to a dilated electronic kerneloid.

Also, is more realistic to consider an exponential variation of the form corresponding to the scalar nuclear potential (2), of the magnetic induction $B^{*}\left(d_c\right)$ , caused by an identical variation of the quasielectron’s ${\Gamma }_{\mu }{}^{*}$  – vortex as the electron’s density, conform to CGT: ${\rho }_{\mu }\left(r\right)={\rho }_e\left(r\right)={\rho }_e{}^0\cdot e^{-r/}{}^{\eta *}$ ,  which –by the relations: $B_{\mu }\left(r\right)=k_1{\rho }_{\mu }\left(r\right)c$ , $(k_1=4\pi a^2/e)$ , of CGT gives a magnetic potential:

$V_{\mu }\left(r\right)={\mu }_e{}^{*}\cdot B_{\mu }\left(r\right)=\mathrm{½}\left({}^2{/}_3\right)\left(ec{d}_c\right)(4\pi a^2/e)c\cdot {\rho }_e{}^0\times e^{-r/}{}^{\eta *}$   

$\Rightarrow V_m\left(r\right) =\left({}^4{/}_3\right)(\pi a^2{c}^2{d}_c)\cdot {\rho }_e{}^0\cdot e^{-r/}{}^{\eta *}; (\eta *\approx 0.8)$   (17)

With ${\rho }_e{}^0\approx 2.2x{10}^{14}kg/m^3$ , for $d_c{}^i=0.0\left(4\right)fm$ ,

it results: $V_{\mu }\left(d_c{}^i\right)=4.3x{10}^{-3}MeV$ , on radial direction, (and higher on the axial direction), so- of neglijible value.

It results that only the electrostatic interaction would explain the constituent u-quarks’ stability, which – for $d_c=d_c{}^i$ , gives a total interaction force between paired current u-quarks or pseudo-quarks:

$F_q{}^i\left(d_c{}^i\right)={\left(d_c{}^m/d_c{}^i\right)}^2{F}_q\left(d_c{}^m\right)\approx 2.5x{10}^{4}N$ ;  (18a)

$V_q(d_c{}^i)=d_c{}^{i}x{F}_q\left(d_c{}^i\right)=6.87MeV$ .  (18b)

At the proton’s transforming into quark-gluon plasma, the energy of $~175MeV$ is distributed to a number $N_u=938MeV/2.895MeV=324$ current u-quarks, resulting a value of $~0.54MeV$ per current u-quark - of $~14$ times lower than the value:

$V_q\left(d_c{}^i\right)=6.8MeV$   .

      But if we calculate the corresponding density of E-field’s quanta (of light vector photons, “vectons” –in CGT) at the electron’s surface:${\rho }_E(r_e{}^{*})$ resulting conform to the relations:

$e=\epsilon \cdot 4\pi a^{2}E\left(a\right)\approx \epsilon \cdot 4\pi r_e{{}^{*}}^{2}E(r_e{}^{*})$ ,  (19)

$\Rightarrow a^2{\rho }_E\left(a\right)\approx r_e{{}^{*}}^2{\rho }_E(r_e{}^{*})$   ,

and it results: ${\rho }_E(r_e{}^{*})={(a/r_e{}^{*})}^2{\rho }_E\left(a\right)$ ,  

i.e. of $~1.96x{10}^4$ times higher than the density of E-field’s quanta at the electron’s surface, ( 10¹⁸ kg/m³ which would diminish the density of the quasielectron’s magnetic moment, ${\mu }_e{}^{*}$ ,conform to CGT. This fact indicates the necessity to consider a slower variation of the r_E –density inside the classic volume (of a-radius), of the form: ${\rho }_E(r_e{}^{*})=(a\surd a/r_e{}^{*}\surd r_e{}^{*}){\rho }_E\left(a\right)$ , corresponding to the combination between a cylindrical distribution and a spherical one, specific to a vortex with precession movement,  which gives an attraction force between two quasielectrons:

$F_e\left(d_i\right)=-e^{*}\cdot E^{*}\left(d_i\right)=-\left({}^2{/}_3\right)e\cdot (a\surd a/d_i\surd d_i)E^{*}\left(a\right)$   ;
$\Rightarrow F_e\left(d_i\right) =-4.67x{10}^{3}N;(E^{*}\left(a\right)=\left({}^2{/}_3\right)e/8\pi {\epsilon }_0{a}^2)$      (20)

The repulsion force between two quasi-electrons with identical $e^{*}$ -charge has the same form but with $d_i’=\surd 2d_i$ , resulting a total force of attraction between two adjacent ‘gluols’ of a pair of current u-quarks or pseudo-quarks:

$F_q(d_i)={\text{-2e}}^{\text{*}}\cdot {\text{E}}^{\text{*}}{\text{(d}}_{\text{i}}\text{)}\left(\text{1-}\frac{\text{1}}{\sqrt{\text{2}}\sqrt{\sqrt{2}}}\right)=\text{-2}\cdot {\left(\frac{\text{2}}{\text{3}}\right)}^2\frac{a\sqrt{a}}{d_i\sqrt{d_i}}\frac{e^2}{8\pi {\epsilon }_0{a}^2}\left(1-\frac{1}{1.41\cdot \sqrt{1.41}}\right)=\text{ -3}{\text{.76x10}}^{\text{3}}\text{N}$  (21)

Because $F_e\left(d_i\right)=-\nabla V_e\left(d_i\right)$ and $\left(r^{-1/2}\right)=r^{-3/2}=r^{-1/2}\cdot r^{-1}$ , we have:$V_e\left(d_i\right)=d_i\cdot F_e\left(d_i\right)=-1.284MeV$  

and:$V_q\left(d_i\right)=2V_e\left(d_i\right)[1-1/\surd 1.41]=0.405MeV$ /current u-quark/pseudoquark– value which is close to the value of 0.54 MeV/current u-quark (corresponding to $T_c\approx 2x{10}^{12}K$ ) and which ensures a constituent u/d-quark’s stability (without a “bag”model of nucleon) until an impact energy: $E_i=N_u\cdot 0.405 =324x0.405\approx 131MeV$ - corresponding to a critical temperature $T_c\approx 1.47x{10}^{12}K$ ,  that is lower than the Hagedorn temperature of quark-gluons forming:  $T_H\approx (1.8÷1.9)x{10}^{12}K$ ,$(150÷160MeV)$ but is close to the value: $T_c= E_{th}/k_b=1.7x{10}^{12}K$ , obtained with $E_{th}\approx ħc/a_n$ , ( $a_n$ – the scalar nucleon’s radius)- identified theoretically as threshold energy of quark-gluons plasma producing corresponding to the characteristic scale energy of a degenerate ideal gas of ultra-relativistic identical fermions (Fermi energy),²¹ with $a_n=a=1.41fm$ , resulting that:

$E_{th}\approx ħc/a=140MeV$ .

Supposing that the constituent quarks of a nucleon are maintained inside its impenetrable quantum volume by only the interaction energy of the current u-quarks/pseudoquarks of two lateral surfaces (Figure 5a), because the constituent quarks u/d are linked radially by the binding energy of $\text{~}$ 4 current u/quarks/pseudoquarks per preonic layer and because they have 4 preonic layers, (Figure 2), the binding energy per constituent quark radially coupled results of approximate value:

$E_b{}^r=4x4x0.4=6.4MeV$ .

So, supposing that a half of the impact energy $E_i=131MeV$ is transmitted as kinetic energy equally to the three nucleonic constituent quarks, it results that the integrity of the constituent quarks will be maintained but they will receive a mean kinetic energy: $E_i{}^q=E_i/2x3\approx 21.8MeV>E_b{}^r,$ that cannot disintegrate the constituent quark but that can generate the separation of the constituent quarks. This fact can explain the transferring of a constituent quark from a baryon to its interaction partner but not explain the fact that the proton is stable until the Hagedorn temperature of quark-gluons forming: $T_H\approx (1.7÷1.8)x{10}^{12}K,$ $(150÷160MeV)$ , without a “bag”model of nucleon.     However, the proton’s stability can be explained by the conclusion that all the proton’s constituent quarks are axially coupled. Because in this case the constituent quarks are linked by the binding energy between the current quarks/pseudoquarks of four $z^0$ –preons , i.e. by 7x6 = 42 “gammonic” $\left(e^{*+}{e}^{*-}\right)$ - pairs per $z^0$ –bosons, corresponding to a force:

$F_t\left(d_c\right)=F_e\left(d_c\right)+F_{\mu }\left(d_c\right)\approx F_e\left(d_c\right)$  (by neglecting the magnetic force $F_{\mu }$ ) and to a binding energy:

$E_b{}^a=V_e{}^a=42x{V}_e\left(d_i\right)=42x1.284=53.9MeV$ per axially coupled $z^0$ –boson.

So, supposing that the impact energy E_i is not distributed as vibration energy to the proton’s current quarks/pseudoquarks and is entirely transmitted axially as kinetic energy to the last  constituent quark (axially coupled by 3 $z^0$ -preons and a z⁺ -preon), it results that the proton can be maintained in an excited state until the impact energy:$E_i(T_H)\approx 4E_b{}^a=215.6MeV$ corresponding  to a temperature $T_C=2.5x{10}^{12}K$ , conform to the model. The previous conclusion results by the fact that –for a constituent quark composed of layers of $z_2$ – and $z_{\pi }$ - bosons, the quasielectrons of the same axial direction are coupled magnetically also axially (attractive) but with opposed electric charges for the adjacent quasielectrons, the interaction force between two quasielectrons on the axial direction being higher than the force on the radial direction.

Because the force F_q is generated between each adjacent current u-quarks or pseudo-quarks, this theoretic result can explain the high stability of the proton, this force determining a strong interaction and a low vibration energy of their mass and of their current quarks/pseudo-quarks. The instability of other elementary particles is explained in this case by a less stable quasi-crystalline structure of their constituent quarks (with more network’s vacancies) which determine a higher vibration energy of their current quarks/pseudo-quarks and by an arrangement with non-axially coupled constituent quarks.

This particularity of the model, correlated with the higher stability of the nucleonic constituent quarks, can explain also the fact that the quark-gluons plasma producing is characterized by a great increase in the number of heavier quark pairs in relation to the number of up and down quark pairs. Another argument for the conclusion that the quarks can be transferred to an impact partner as constituent quarks is the dependency of the lifetime of a non-nucleonic particle on the constituent quarks number:

Considering the ${\mu }^{\pm }$  -lepton (having a lifetime:${\tau }_0=2.2x{10}^{-6}sec$ ) as single-particle cluster and taking into account that the majority of the elementary baryonic astro-particles (with n=3 quarks have a lifetime ${\tau }_B\approx {10}^{-10}sec$ . and the majority of mesons (n=2) have a lifetime ${\tau }_m\approx {10}^{-8}sec$ . at an ordinary temperature: T = 300K of the particles’ environment, is deduced in CGT a semi-empiric relation for the lifetime ${\tau }_k({\epsilon }_v)$ of the cosmic particles,  considering its dependence to the intrinsic  temperature T_q and to the vibration energy ${\epsilon }_v$ of the component current quarks, which- according to CGT, generate a partial destruction of the particle’s intrinsic vorticity, with the loosing of a part of $\Delta m_p$   internal ‘naked’ photons which gives the  mass of the  quark’s shell, as in the case of a nucleus’ hot’ forming from nucleons,  according to the model,⁶ i.e. with: ${\tau }_k~1/\Delta m_P\left(T\right)$ , resulting:

${{\displaystyle \tau }}_k=\frac{{{\displaystyle \tau }}^{\text{0}}}{{{\displaystyle k}}_v\cdot {{\displaystyle 10}}^{2n}}\approx \frac{{\tau }_0\cdot m_p}{\Delta m_P\left(T\right)};{{\displaystyle \tau }}^{\text{0}}\cong 3x{{\displaystyle 10}}^{--14}sec.;{{\displaystyle k}}_v=\frac{{{\displaystyle \epsilon }}_v}{{{\displaystyle \epsilon }}_v^o}=\frac{n\cdot {{\displaystyle \nu }}_i}{{{\displaystyle \nu }}_c^o}=\frac{n\cdot T}{T_N};{\text{ T}}_{\text{N}}\cong 2x{\text{10 }}^{\text{12}}\text{ K}$   (22)

in which:${\nu }_c{}^0$ represents the critical frequency of the phononic energy ${\epsilon }_v{}^0$ of quark vibration at which the proton’s  disintegration take place:

${\nu }_c{}^0={\nu }_c(T_{N }\approx 2x{10}^{12}K)\approx 4x{10}^{22}Hz$   . 

The relation (22) is specific to non-axially coupled quarks (to non-nucleonic particles) and explain the fact that the heavy baryons with composite heavy quarks can have a longer lifetime at T®0K but cannot have a long life at an ordinary temperature.⁶

The naturalness problem: electric interaction between quarks or ‘bag’ model?

The resulted hybrid model has some lacs of naturalness “inherited” from models of the Quantum Mechanics:

A first lack of naturalness of the resulted hybrid model results from the fact that it was supposed that the entire mass of the nucleon is contained by its current quarks and pseudoquarks, i.e. –by the kerneloids of the quasielectrons of the valence current quarks and of the ‘gluols’, even if it is known that the root-mean-square radius of the nucleon is of $\text{~}$ 0.841¸0.88 fm²² and its scalar radius is: r_n »1.25¸ 1.4 fm –in concordance with the known formula of the nuclear radius: $R_N\approx r_n\cdot A^{1/3}$ , (A- the atomic mass). More realistic - in this case, is to consider that only a fraction from the entire $m_e{}^{*}$ - mass of the quasielectrons is contained by their volume of mechanic radius ($0.01÷0.022fm$ ), i.e. –that only a part of the nucleon’s mass is contained by its ‘impenetrable’ quantum volume, the rest part being contained by the nucleon’s volume of scalar radius r_n , in the form of kinetized photons of electrostatic interaction- as in the CGT’s model.

Another lack of naturalness of the resulted hybrid model results from the fact that it was considered an electric charge of the current u-quarks reduced (only) to the value of (²/₃)e also for very small interdistances between quasielectrons ($\text{~}$ 0.04 fm), (as in the Standard Model), without knowing the nature of the e-charge. In the Quantum mechanics, this fact is not a problem, because it is considered that the electrostatic interaction is realized by change of some virtual photons of the E-field. In CGT, the e-charge is proportional with the electron’s classic interaction surface: $S_i{}^e=\pi r_e{}^2$ , (e-charge in its surface) conform to the relation: $e=4S_i{}^e/k_1=4\pi a^2/k_1$ , $(a=1.41fm;k_1=4\pi a^2/e=1.56x{10}^{-10}{m}^2/C)$ , the electric interaction force between two electrons resulting by a pressure of quanta, in accordance with the classic relation:

$F_e\left(r\right)=e\cdot E_e\left(r\right) =4\pi a^2{\rho }_v\left(r\right)c^2$ ,  (23)

${\rho }_v\left(r\right)c$ being the impulse density of the E-field’s quanta (light vector photons)⁶ at the distance r from the electron’s center, interacting with the $S_i{}^e$ –section of the second electron. But if r << a, this $S_i{}^e$ –section of electric interaction cannot remain at the value $\pi a^2$ , it being reduced to the value:$$S_i{}^{’}=\pi r^2=\pi r_i{}^2\left(r_i=d_i/2\right)$$ $S_i{}^{’}=\pi r^2=\pi r_i{}^2\left(r_i=d_i/2\right)$ corresponding to a reduced charge:

$e^{*}=e\cdot {\left(r_i/a\right)}^2$ , giving a reduced F- force.

It is possible to recalculate the constant k₁ with r_i instead of a (k₁^* = 4pr_i²/e) and with the relation:

$e\cdot E_e\left(a\right) = 4\pi a^2{\rho }_v\left(a\right)c^2= 4\pi r_i{}^2{\rho }_v{}^{*}\left(a\right)c^2$ ;  (24)

$({\rho }_v{}^{*}\left(a\right)=a^2{\rho }_v\left(a\right)/r_i{}^2= a^2{\mu }_0/{\left(k_1{r}_i\right)}^2)$  

but in this case will be relative difficult to explain the Lorentz force as quantum force of Magnus type, as it is explained in CGT.⁶ Also, eq. (24) gives a value ${\rho }_v{}^{*}\left(a\right)\approx 2x{10}^{17}kg/m^3$ (comparable with the nucleon’s density) and ${\rho }_v{}^{*}\left(r_i\right)={\rho }_v{}^{*}\left(a\right)(a\surd a/r_i\surd r_i)\approx {10}^{20}kg/m^3$   value: , (much higher than the nucleon’s density), so- un-plausible, even if we can consider the vector photons of the E-field as “virtual” photons but in the sense that they do not contribute to the particle’s inertial mass (being weakly linked) – conform to CGT.

In this case it results that the magneto-electric interaction between the particle’s quasielectrons (forming their quarks), even it can explain the quarks’ forming, it explain not enough naturally the constituent quark’s stability and the proton’s stability until the critical temperature $T_c\approx T_H$ . But if a relative small fraction of the photons forming the photonic shell of the nucleon’s impenetrable volume of (theoretic) radius:$a_i\approx 0.6fm$ (retained by the total vortical field of the superposed ${\Gamma }_{\mu }{}^{*}$ -vortices of the degenerate electrons)⁶ have kinetic vibrations with radial component at the surface of the nucleon’s impenetrable volume, the maintaining of all current quarks and pseudo/quarks (forming the constituent quarks) inside this volume ${\upsilon }_i\left(a_i\right)$ can be explained (also) by a “bag” model as in Ref.¹⁹

The nuclear interaction between nucleons in a hybrid quark model

For the explaining the nuclear interaction between nucleons, we observe that -if the nucleons are separated at a distance $d_c>2r_p\approx 1.7fm$ , the magnetic and electric force $F_t\left(d_c\right)=F_m\left(d_c\right)+F_e\left(d_c\right)$ cannot explain the mean value of the binding energy per nucleon characteristic to the stable nuclei: E_B » 8.5 MeV, because the fact that the total magnetic moment of the constituent (u/d)- quark and its electric charge is given only by the valence current quark , at a value that cannot explain the E_B- binding energy: ${\mu }_u\approx 2.49{\mu }_N$ , respective - ${\mu }_d\approx -2.2{\mu }_N$ , ( ${\mu }_N$ –nuclear magneton), resulted by the values characteristic to the nucleons: ${\mu }_p=2.79{\mu }_N$ , respective - ${\mu }_n=-1.91{\mu }_N$ .

But taking into account the vortical nature of the magnetic field⁶ and the principle of quantum fields’ superposition, it is possible to use the eq. (2) of CGT if we consider that – at a normal nuclear temperature (${10}^8÷{10}^{10}K$ ), the constituent quarks have all the valence quarks and $z^0$ - preons inside the nucleon’s impenetrable volume of a radius $r_i\approx 0.6fm$   , (the radius  r_p = 0.85 fm corresponding to a dilated (maximally excited) impenetrable volume of $T\approx {10}^{12}K$ ).

The mean interdistance d_i  between the preonic quasielectrons results- in this case, (conform to Figure 4), of value:$d_c{}^i=\left({}^2{/}_3\right)r_i/9=0.0\left(4\right)fm$ and corresponds to a dilated electronic kerneloid, of radius $r_e{}^{*}\approx 0.022fm$ (given by the internal vibrations of the electronic super-dense centroid, of radius $\text{~}$ 10^-18m), filled with heavy photons having an inertial mass m_f of radius ~ 10^-18 m (and an evanescent part) but containing only a fraction from the entire m_e^*- mass of the quasielectron, the rest part of its mass:$\Delta m_e{}^{*}$ forming the photonic shell of the quasielectron’s kerneloid, which by summation to all nucleon’s volume, gives the photonic shell of the nucleon’s impenetrable volume: $\Delta m_n=\sum \upsilon \Delta m_e{}^{*}$ , of density ${\rho }_n\left(x\right)$ with exponential decreasing (Figure 5b) and of equal value with the density of the superposed quantonic vortices ${\Gamma }_{\mu }{}^{*}$ of the protonic quasielectrons forming the protonic N^p –cluster, conform to CGT:⁶ ${\rho }_n\left(r\right)\approx \sum {\rho }_m={\rho }_n{}^o{e}^{-r/}{}^{\eta *}$ , in concordance with the expression:$\rho =m\cdot \psi 2^{}$ used by quantum mechanics and with eq. (2) for which in CGT were obtained the values:${\rho }_n{}^o\approx N^p\cdot {\rho }_e{}^o=5.04x{10}^{17}kg/m^3$ , $({\rho }_e{}^0=22.24x{10}^{13}kg/m^3)$ ; $\eta *=0.8fm$ , giving- with ${\upsilon }_i\left(a_i\right)=0.9f{m}^3$ , $V_s{}^0=127.5MeV$ and:$V_s\left(d=2fm\right)\approx 9MeV$ – value specific to the mean binding energy per nucleon in the nuclei with the most strongly bound nucleons, (9.14 ¸9.15 MeV/nucleon for ⁵⁶Fe, ⁵⁸Fe, ⁶⁰Ni, ⁶²Ni).

The mass:$\Delta m_n={\sum }_u\Delta m_e{}^{*}$ of the photonic shell of the nucleon’s impenetrable volume is maintained by an attraction force deriving from a potential of the Eulerian form (2) generated by the superposed quantonic vortices ${\Gamma }_{\mu }{}^{*}$ of the protonic quasielectrons but with a smaller impenetrable quantum volume, specific to the vector photons ${\upsilon }_f(r_f\approx {10}^{-18}m)$ .

Because- conform to eq. (5) of CGT, the preonic and the quarcic clusters retain (also at their releasing), by their vortical field (given by superposed G_m^* -vortices), a photonic shell of mass proportional with the number of  kernels of quasielectrons which compose the preonic boson’s kernel, i-e- corresponding to the boson’s effective mass, this explains the fact that at the quark’s releasing from an interacting particle it carries the entire its rest mass, conform to eq. (9). Because- for this quark model, also the bag model of CGT¹⁹ can be used, explaining also the asymptotic freedom of quarks’ interaction, it results in this case, by CGT, a hybrid quark model more realistic and more natural than that of the Standard Model, which can explain also the strong interaction, without the concept of “color charge”.

It results that the proposed hybrid model of constituent quark, which uses also basic concepts of the S.M. which seem experimentally sustained, can explain coherently the constituent quarks forming from current quarks and “gammonic” ‘gluols’ –in concordance with the experimentally evidenced possibility of paired quarks forming from relativist jets of negatrons and positrons, but also the elementary particles forming, by considering that the negatrons and positrons which are not mutually annihilated,  form ‘gammonic’ gluols and thereafter- current and constituent quarks- in a quasi-crystalline form, by magnetic and electric interactions between the paired quasielectrons (degenerate electrons), without the concept of ‘color charge’, which results more conventional than real (phenomenological), in this case.

Apparently, these magneto-electric interactions can explain also the proton’s stability until the critical temperature $\text{~}$ 2x10¹² K, but –by CGT, it is argued that- for interdistances r < a = 1.41 fm, the relative value of the electric charge (which enters in the expression of the E-field’s intensity) decreases with r² and only the ‘bag’ model can explain naturally the quarks’ maintaining inside the nucleon’s ‘impenetrable’ volume.  So, a hybrid model which use an effective radius r << a has yet some naturalness problems, “inherited” from the Quantum Mechanics’ models of electron and of electric interaction.

However, the resulted hybrid model can explain coherently the possible mechanism of the quarks’ forming from relativistic jets of electrons and positrons and the particle’s forming, without the concept of “color charge”, and the fact that in the strong interactions the sum rule can be applied correspondent with the transferring of some quarks from an interacting particle to another with the entire or almost entire their constituent mass, as in the reaction (9), which can be explained by the contribution of the mass M = Q/c² of some ‘gammonic’  (e^-e⁺)- pairs of the quantum vacuum.

It shows also that the nucleon model used by CGT is semi-compatible with that of the Standard Model but more natural than it, avoiding also the concept of “virtual” gluon/boson- a concept relative vaguely defined. Also, it suggests that the mechanism of paired current u-quarks forming from gluons, used by the S. M., can be plausible in conformity with the mass conservation law only if the quantum vacuum contains thermalized (slowed) real “gammons”- considered as (e⁺e^-)^*-pairs of degenerate electrons. At T®0K, these “gammons” have low interaction with the electromagnetic radiation, being electrically neutral and quasi-stable, so they can be an important component of the “dark” matter.

Also, it can also explain the natural forming of super-heavy particles, of “oh my God” type,²³ having energy of $~3.2x{10}^{20}eV$ , by the conclusion of super-heavy “gammonic” cluster’s forming at T®0K, as Bose-Einstein condensate of “gammons”.⁷

    The main experiments which are concordant with the proposed hybrid model are:

1. the transforming of gamma quantum of 1MeV into a pair (e⁺e^-) by an electrostatic energy $E_e\ge 2m_e{c}^2$ and the experimentally obtaining of “gammons” in the form of quanta of “un-matter” plasma,²⁴ (which argues the model of gamma quantum of 1MeV as pair of degenerate electrons and the possibility of particles’ forming from “gammons”);
2. the experimentally obtaining of a Bose-Einstein condensate of photons, (a “super-photon”), by a German team,²⁵ indirectly proving the existence of the rest mass of photons, considered in CGT, as in the case of the ‘dark photon’ theorized in the quantum mechanics);
3. the field-like nature of the ‘dark’ energy evidenced in astrophysics²⁶ (explaining the magnetic field/energy);  
4. the experimentally obtaining of bosons (even W, Z-bosons) and q -q* pairs by (e^- -e⁺) or (e^--p⁺)-interactions¹⁵ and the charm-quark decaying into muons and electrons,²⁷ (which sustains the possibility of quarks’/particles’ forming as clusters of “gammonic” pairs of degenerate electrons- a more natural explanation than those used by the M. which considers the creation of a q -q* pair by a reaction:$\left(e^{-}-e^{+}\right)\to q-\overline{q}$ via a virtual photon). 

None.

None.

1. Patrignani C. (Particle Data Group), "Quarks. Chin Phys C. 2016;40:100001.
2. Andersson B, Gustafson G, Ingelman G, et al. Parton fragmentation and string dynamics. Phys Rep. 1983;97(2–3):31–145.
3. Yndurain F. Limits on the mass of the gluon. Physics Letters B. 1995;345(4):524.
4. Precision pins down the electron’s magnetism. 2006.
5. ZEUS Collaboration. Limits on the effective quark radius from inclusive e–p scattering at HERA. Physics Letters B. 2016;468–472.   
6. Arghirescu M. The Cold Genesis of Matter and Fields. Ed. Science PG. 2015.
7. Arghirescu M. A model of particles cold forming as collapsed Bose–Einstein condensate of gammons. PAIJ. 2018;2(4):260–267.
8. Arghirescu M. An Explanatory Model of Heavy Quarks and Particles Generating resulted by a Cold Genesis Theory. Theor Phys Lett. 2021;9(11).
9. Souza, M E. Calculation of almost all energy levels of baryons. Papers in Physics. 2011.  
10. Krasznahorkay AJ. Observation of Anomalous Internal Pair Creation in 8Be: A Possible Signature of a Light, Neutral Boson. 2015.      
11. Krasznahorkay AJ. New evidence supporting the existence of the hypothetic X 17 particle. 2019.
12. Saint Venant A. Memoir on the theory of resistance of fluids. Solution of the paradox proposed to this subject by d’Alembert to the geometres. Comparison of the theory with the experiments. Reports of Seances de l’Academie des Sciences. 1847;24:243–246.
13. Yan Y, Tegen R. Scattering and Nucleon Quark core. Sci Asia. 2001;27:251.    
14. Milonni PW. The Quantum Vacuum–An Introduction to Quantum Electrodynamics. Ed. Academic, N. Y. 1994.
15. Truten IV, Korchin Al Yu. Energy correlation of bottom quarks from decays of top quarks in electron–positron annihilation. 2022.
16. Carrigan RA Jr. Compound Quarks as an Explanation for the Apparent Quark Mass Spectrum. Fermi Nat. Accelerator Lab., Batavia, Illinois, 60510, 1978.
17. Sakharov AD. Mass formula for mesons and baryons. Zh Eksp Teor Fiz. 1980;78;2112–2115.         
18. Pohl R, Antognini A, Nez F, et al. The size of the proton. Nature. 2010;466(7303):213–216.
19. Arghirescu M. The nuclear force explaining by a bag model resulted from a vortexial, cold genesis model of nucleon. Phys Astron Int J. 2018;2(4):349‒358.        
20. Harris SE, Hau LV. Nonlinear Optics at Low Light Levels. Phys Rev Lett. 1999;82:4611.
21. Apostol M. Hadronization of the quark–gluon plasma. Romanian Reports in Physics. 2007;59(2):249–260.
22. Sick I, Trautmann D. Proton rms–radii and electron scattering. 2014.
23. Bird DJ, Corbato SC, Dai HY. Detection of a cosmic ray with measured energy well beyond the expected spectral cutoff due to cosmic microwave radiation. The Astrophys J. 1995;441:144.
24. Sarri G, Poder K, Cole J, et al. Generation of neutral and high–density electron– positron pair plasmas in the laboratory. Nature Comm. 2015;6:6747.
25. Dung D, Kurtscheid C. Variable potentials for thermalized light and coupled condensates. Nature Photonics. 2017;11:565–569.       
26. Gong–Bo Z, Raveri M, Pogosian L, et al. Dynamical dark energy in light of the latest observations. Nature Astronomy. 2017;1:627–632.
27. Cliff Harry. Evidence of brand new physics at CERN?. The Conversation. 2021.