A Gamma-ray in a uniform compton scatterer

doi:10.15406/paij.2018.02.00144

eISSN: 2576-4543

Physics & Astronomy International Journal

Review Article Volume 2 Issue 6

A Gamma-ray in a uniform compton scatterer

Vladimir Uchaikin

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Professor, Uljanovsk State University, Russia

Correspondence: Prof Vladimir Uchaikin, Uljanovsk State University, L.Tolstoi str. 42, 432000 Russia, Tel 79876875971

Received: February 01, 2018 | Published: December 6, 2018

Citation: Uchaikin V. A Gamma-ray in a uniform compton scatterer. Phys Astron Int J. 2018;2(6):573-576. DOI: 10.15406/paij.2018.02.00144

Download PDF

Abstract

The structure of a narrow ray of gamma radiation propagating through a medium filled with free electrons (called Compton scatterer) is investigated. The dual representation is used including primary (basic) and adjoint forms of kinetic equations. In the ray propagation problem primary form possesses cylindrical symmetry whereas the adjoint form (in case of isotropic detector in an unbounded homogeneous medium) has the spherical symmetry. The analysis performed on the base of adjoint function singularities shows, in particular, that in a vicinity of the narrow gamma-ray single-scattered radiation predominates over all other components. Analytical representation of the field in the vicinity of a cylindrical primary ray has been found. The result can be important in gamma astronomy processing.

Keywords: Compton Scatterer, neumann series, boltzmann equation

Introduction

The concept of adjoint function (or importance function) can be unlocked as follows. Let the problem under consideration requires finding some linear functional
$J [f (\cdot)]=(P, f) \equiv \int P (x) f (x) d x$ (1)
from a solution of the equation

$L f (x) = Q (x),$ (2)

Describing the transport of particles in a medium from a source with phase density $Q (x)$ immersed in a medium, interaction of which with the particles is described by the operator L. In the problem under consideration, $Q (x)$ may denote the flux of photons, or their concentration, or some other local characteristics of the photon field at a point $x = (r, p)$ of the phase space. For the sake of convenience, we will represent the photon momentum $p$ through the pair of variables $Ω = p / p$ (the direction unit vector) and $E = cp$ (photon’s energy)

The direct way of finding the value of the functional (1), expressing the reading of a photon detector, lies through solving of the kinetic equation (2) and computing integral $J = \int f^{+} (x) Q (x) dx$ over the photon field with a weighting function $P (x)$ expressing the contribution of a single photon placed at point X into resulting reading of the detector. But this is not a unique way to reach this result. Another way is based on the other equivalent representation of the detector reading,1−3 using so-called adjoint (or importance) function $f^{+} (x)$ being a solution of the adjoint (in Lagrange’s sense) equation
$L^{+} f^{+} (x) = P (x) .$ (3)

By definition, the primary $L$ and adjoint $L^{+}$ operators are connected via relation

$(f^{+}, Lf) = (L^{+} f^{+}, f) .$

Inserting now Eq.(2) into the LHS of the latter equation and Eq.(3) into the RHS of it, and using Eq.(1), we understand that numerically $f^{+} (x_{0})$ is the detector reading under condition that the source is localized at the point $x_{0}$ and has a unite power: $Q (x) = δ (x - x_{0})$ . A more deep exposition of the concept of the importance function is given in books.¹⁻³

Integral equations and neumann series

The mathematical description of penetration of gamma radiation (X-rays) through a scattering matter is given in the well-known monograph.^4,5 Primary transport equation (2) is written as a linearized kinetic Boltzmann equation, for time-independent problem having the form:

$\begin{array}{l} Ω \cdot \nabla I (r, Ω, E) + μ (r, E) I (r, Ω, E) = Q (r, Ω, E) + \\ \int dΩ \int {dE}^{'} μ_{s} (r, E^{'}) I (r, {ΩE}^{'}) W ({ΩE}^{'} \to Ω, E) . \end{array}$ (4)

Here $I = I (r, Ω, E)$ denotes the differential intensity (so, $Id S d Ωd E$ is a mean number of particles, crossing over a unit elementary area $d S ⊥ Ω$ and belonging to intervals $dΩ \times dE$ ), $μ$ and $μ_{s}$ are linear attenuation (total and scattering) coefficients $Q (r, Ω, E)$ is the source phase density, $W$ the scattering indicatrix, normalized to 1:

$\int_{4 π} dΩ \int_{0}^{E^{'}} dEW ({ΩE}^{'} \to Ω, E) = 1 .$

The correspondent adjoint function is of the form:

$\begin{array}{l} - Ω \cdot \nabla I^{+} (r, Ω, E) + μ (r, E) I^{+} (r, Ω, E)= P (r, Ω, E) + \\ \int d Ω \int d E μ_{s} (r, E) W (Ω, E \to Ω', E^{'}) I^{+} (r, Ω', E^{'}) . \end{array}$ (5)

Both the equation can be transformed to the equivalent integral forms:⁶⁻⁷

$I (r, Ω, E)= \int_{0}^{\infty} e^{- τ (r, r - Ω ξ, E)} \tilde{Q} (r - ξ Ω, Ω, E) d ξ$ (6)

with

$\tilde{Q} (r, Ω, E)= Q (r, Ω, E) + \int_{4 π} d Ω' \int_{E}^{E^{'}} d E^{'} I (r, Ω', E^{'}) μ_{s} (r, E^{'}) W (Ω', E^{'} \to Ω, E),$ (7)

and

$I^{+} (r, Ω, E)= \int_{0}^{\infty} e^{- τ (r, r + Ω ξ; E)} \tilde{P} (r + Ω ξ, Ω; E) d ξ,$ (8)

with

$\tilde{P} (r, Ω, E)= P (r, Ω, E) + μ_{s} (r, E) \int_{4 π} d Ω' \int_{0}^{E} d E^{'} I^{+} (r, Ω, E) W (Ω, E \to Ω', E^{'}) .$ (9)

In these equations, $τ (r, r \pm ΩξE)$ denotes the optical distance between the points for $γ$ -quanta with energy $E$ indicated in the argument:

$τ (r, r \pm Ω ξ; E)= \int_{0}^{ξ} μ (r \pm Ω ξ^{'}) d ξ^{'} .$ (10)

Inserting (7) into (6) and (9) into (8), we will see initial terms of the Neumann series representing solution of the integral equations. The terms with $n = 0$ relate to non-scattered radiation, whereas the other terms describe contribution of scattered quanta (the integer $n = 1, 2, 3, ...$ indicate scattering multiplicity. In particular,

$I_{0} (r, Ω, E)= \int_{0}^{\infty} e^{- τ (r, r - Ω ξ; E)} Q (r - Ω ξ, Ω, E) d ξ,$ (11)

$I_{0}^{+} (r, Ω, E)= \int_{0}^{\infty} e^{- τ (r, r + Ω ξ; E)} P (r + Ω ξ, Ω, E) d ξ,$ (12)

$I (r, Ω, E) = \sum_{n =0}^{\infty} I_{n} (r, Ω, E), I^{+} (r, Ω, E) = \sum_{n =0}^{\infty} I_{n}^{+} (r, Ω, E),$

and next terms are computed by induction:

$\begin{array}{l} I_{n} (r, Ω, E)= \int_{0}^{\infty} d ξ e^{- τ (r, r - Ω ξ; E)} μ_{s} (r - Ω ξ, E) \times \\ [\int_{4 π} d Ω' \int_{E}^{\infty} d E^{'} W (Ω', E^{'} \to Ω, E) I_{n - 1} (r - Ω ξ, Ω, E^{'})], n = 1,2, \dots \end{array}$ (13)

$\begin{array}{l} I_{n}^{+} (r, Ω, E)= \int_{0}^{\infty} d ξ e^{- τ (r, r + Ω ξ; E^{'})} μ_{s} (r + Ω ξ, E) \times \\ [\int_{4 π} d Ω' \int_{0}^{E} d E^{'} W (Ω, E \to Ω', E^{'}) I_{n - 1}^{+} (r + Ω ξ, Ω', E^{'})], n = 1, 2, \dots \end{array}$ (14)

A point mono-directional source

Now we consider the field created by a point source of gamma-quanta placed at the origin O of the Cartesian coordinate and directed along z-axis, and let the field be measured by a point isotropic detector showing the integral

$J = \int_{4 π} d Ω \int_{0}^{\infty} d E P (E) I (r_{1}, Ω, E)$

with standing for the detector response to a single photon with energy E. Thus, the free term in the adjoint equation (5) takes the form

$P (r, Ω, E)= P (E) δ (r - r_{1}),$ (15)

Where as the primary equation (4) has it in the form

$Q (r, Ω, E)= δ (r) δ (Ω - Ω_{0}) Q_{0} (E)$ (16)

$Q_{0} (E)$ denotes the source energy spectrum). The medium is supposed to be homogeneous and isotropic, so a suitable choice of coordinate system is dictated by specifics of the source-detector arrangement. An important role in this is given to symmetries, allowing for the reduction of the number of independent variables in the problem and thereby facilitating its solution (Figure 1). As we saw above, the same physical problem is expressed in two different forms differing in the degree of symmetry: Eq.(15) exhibits spherical symmetry whereas Eq.(16) reveals cylindrical one. So, it is naturally to choose the spherical symmetry version, possessing higher degree of symmetry and requiring only one spatial variable $| r - r_{1} |$ . In what follows, we put $r_{1} = 0$ , i.e. combine the origin of coordinates with the detector position, use the vector $r$ for the initial position of the quantum, and introduce the angle $θ$ via relation:

$c o s θ = - \frac{Ω r}{r} .$

On substitution (15) into Eq.(12), we obtain non-scattered term in adjoint function decomposition:

$I_{0}^{+} (r, Ω, E)= \frac{1}{2 π r^{2}} e^{- τ (r, r'; E)} P (E) δ (1 - c o s θ) .$ (18)

For a homogeneous medium $τ (r, r + Ω ξ; E)= μ (E) ξ$ , so

$I_{0}^{+} (r, Ω, E)= \frac{1}{2 π r^{2}} e^{- μ (E) ξ} P (E) δ (1 - c o s θ) .$ (19)

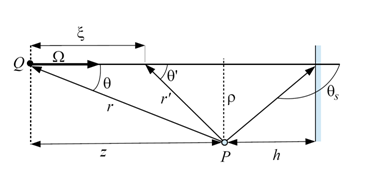
Figure 1Geometry of narrow ray. Q is the source place, P is a counter place.

Computing single scattered intensity, we take into account that the scattering indicatrix includes the delta-function expressing the Compton interrelation between initial quantum energy $E$ , scattering angle $θ^{'}$ and scattered quantum energy

$E_{1} = \frac{E}{1 + (1 - c o s θ^{'}) E / m c^{2}} .$

Denoting $r + Ω ξ$ by $r^{'}$ and the regular multiplier in the indicatrix by $V (c o s θ^{'})$ , we represent the latter as

$W (Ω \to Ω')= V (c o s θ^{'}) δ (E^{'} - E_{1} (c o s θ^{'}, E)),$

where

$c o s θ^{'} = \frac{Ω r'}{r^{'}}$ (20)

and

$V (c o s θ^{'})= \frac{1}{σ} \frac{d σ}{d Ω}$

is the normalized differential cross-section of the Compton scattering. In an explicit form,

$\frac{d σ}{d Ω} = \frac{r_{0}^{2}}{2} {(\frac{E_{1}}{E})}^{2} (\frac{E}{E_{1}} + \frac{E_{1}}{E} - {s i n}^{2} θ^{'})$

(Klein-Nishina-Tamm formula) and

$\begin{array}{l} σ_{ε} = \frac{3}{4} σ_{0} \{\frac{1 + ε}{ε^{3}} [\frac{2 ε (1 + ε)}{1 + 2 ε} - l n (1 + 2 ε)]\} + \\ \frac{3}{4} σ_{0} \{\frac{1}{2 ε} l n (1 + 2 ε) - \frac{1 + 3 ε}{{(1 + 2 ε)}^{2}}\}, ε = \frac{E}{m_{e} c^{2}} . \end{array}$ (21)

Inserting $n = 1$ into Eq.(14), using Eq.(19) and property of delta-function, we arrive at the following expression for single scattering contribution into the sought quantity

$J_{1} = I^{+} (r, Ω, E)= \int_{0}^{\infty} e^{- μ (E) ξ - μ (E_{1}) r^{'}} μ_{s} (E) V (c o s θ^{'}) P (E_{1}) \frac{d ξ}{{r^{'}}^{2}} .$

With fixed variables $r$ and $Ω$ , the variable $ξ$ is uniquely linked with the scattering angle $θ^{'}$ (Figure 1). Applying the sinus-theorem yields interrelations

$r^{'} = r \frac{s i n θ}{s i n θ^{'}} ξ = r \frac{s i n (θ^{'} - θ)}{s i n θ^{'}}, d ξ = r \frac{s i n θ}{{s i n}^{2} θ^{'}} d θ^{'} .$

Using these formulae for passage to other variables leads us to expression

$J = \frac{μ_{s} (E)}{r s i n θ} \int_{θ}^{θ_{s}} e x p \{- \frac{r}{s i n θ^{'}} [μ (E) s i n (θ^{'} - θ) + μ (E_{1}) s i n θ]\} V (c o s θ^{'}) P (E_{1}) d θ^{'} .$ (22)

In case of an infinite homogeneous medium (coefficients $μ$ and $μ_{s}$ are independent of spatial variables), the upper limit of integration $θ_{s} = \infty$ , but this formula can be used and on the plain boundary with an absorbing medium, when the source is in a homogeneous semi-space and the point of measurement is on a plane surface perpendicular to direction $Ω$ . In this case the lower limit of integrating is zero upper limit $θ_{s}$ should be taken $π / 2$

The formulae for single-scattered quanta obtained above, includes multiplier $[rsinθ]^{- 1}$ , which grows unboundedly with decreasing $rθ \to 0$ . Consequently, at small $θ$ or $r$ the rest terms (with n>1) may be ignored.

Singularity of the adjoint function at great depths

Let us pass to the cylindrical coordinate system each point of which is characterized by longitudinal $(z = r c o s θ)$ coordinate (depth) and transverse one $(ρ = r s i n θ)$ (radius). Then

$I_{1}^{+} (r, Ω, E)= \frac{μ_{s} (E)}{ρ} \int_{θ}^{θ_{s}} e x p \{μ (E) ρ ctg θ^{'} - μ (E) ρ cosec θ^{'}\} V (c o s θ^{'}) P (E_{1}) d θ^{'} .$ (23)

Expand the exponential function in series and denote ith term of this series by $φ_{i} : i = 0, 1, 2, . . .$ :

$φ_{0} = \frac{μ_{s} (E)}{ρ} e^{- μ (E) z} \int_{θ}^{θ_{s}} V (c o s θ^{'}) P (E_{1}) d θ^{'},$ (24)

$φ_{1} = μ_{s} (E) e^{- μ (E) z} \int_{θ}^{θ_{s}} [μ (E) ctg θ^{'} - μ (E_{1}) cosec θ^{'}] V (c o s θ^{'}) P (E_{1}) d θ^{'},$ (25)

$φ_{2} = \frac{1}{2} μ_{s} (E) ρ e^{- μ (E) z} \int_{θ}^{θ_{s}} {[μ (E) ctg θ^{'} - μ (E_{1}) cosec θ^{'}]}^{2} V (c o s θ^{'}) P (E_{1}) d θ^{'},$ (26)

and so on.

Let the counter be far enough from the source and from the boundary (i.e. $z > ρ$ and $h < ρ$ ). In this case, $θ \approx \frac{ρ}{z} \to 0$ and $θ_{s} \approx π - \frac{ρ}{h} \to π$ , therefore,

$φ_{0} = \frac{μ_{s} (E)}{ρ} e^{- μ (E) z} \int_{0}^{π} V (c o s θ^{'}) P (E_{1}) d θ^{'} .$ (27)

The integrand in Eq.(25) has a singularity at $θ = 0$ and $θ = π$ . Let us break the integral into three pieces $\int_{θ}^{θ_{s}} = \int_{ρ / z}^{ε} + \int_{ε}^{π - ε} + \int_{π - ε}^{π - ρ / h}$ , where $ε$ is a small positive number choosing in such a way that all terms in this sum are positive. Neglecting the change of $μ, K$ and P in the $ε$ -interval and leaving only singular terms, we obtain

$φ_{1} = μ_{s} (E) e^{- μ (E) z} [μ (E) + μ (E_{π})] V (c o s π) P (E_{z}) ln ρ,$ (28)

where

$E_{π} \equiv E_{1} (cosπ, E) .$

Acting in a similar way, one can show that and next terms in this sum at $ρ \to 0$ do not have singularity.
If the counter is placed on the very boundary, then singularity characterizes only the first term (24) in the expansion of (23)

$φ_{0} = \frac{μ_{s} (E)}{ρ} e^{- μ (E) z} \int_{0}^{π /2} V (c o s θ^{'}) P (E_{1}) d θ^{'} .$ (29)

Let us introduce the notations

$Θ (ϕ, ψ; E)= \frac{2 π}{P (E)} \int_{ϕ}^{ψ} V (c o s θ^{'}) P (E_{1}) d θ^{'},$

and $Θ = Θ (0, ψ; E)$ , then for both above mentioned positions of the counter the expression

$\begin{array}{l} I^{+} (r, Ω, E) \sim I_{0}^{+} (r, Ω, E) + I_{1}^{+} (r, Ω, E) \approx \\ \frac{1}{2 π ρ} [δ (ρ) + μ_{s} (E) Θ] P (E) e^{- μ (E) z}, ρ \to 0, \end{array}$ (30)

stay be valid, if put $θ_{s} = π / 2$ in the boundary case, and $π$ otherwise (more weak logarithmic singularity are omitted). As a result, we get:

$I^{+} (r, Ω, E;)= \frac{1}{2 π ρ} [δ (ρ) + μ_{s} Θ] P (E) e^{- μ z} .$

Let $I_{0} (x, y)$ be the initial profile of the ray at $z = 0$ and $I_{} (x, y, z)$ the ray profile at depth . According to the above result, the latter is composed from two terms: unscattered part repeating the shape of the incident ray, $I^{nsc} (x, y, z)= I_{0} (x, y) e^{- μ z},$ and scattered component

$I^{sc} (x, y, z)= μ_{s} Θ e^{- μ z} \int_{Σ} \frac{I_{0} (x^{'}, y^{'}) d x^{'} d y^{'}}{\sqrt{{(x - x^{'})}^{2} + {(y - y^{'})}^{2}}},$ (31)

where $Σ$ stands for a cross section of the incident ray. The formula establishes the connection between the clear image of the ray given by the unscattered component, and the diffusion "halo," responsible for which is the scattering process. This connection is reminiscent of the relationship known in electrostatics between the charge distribution $σ (x^{'}, y^{'})= μ_{s} Θ I_{0} (x^{'}, y^{'}) e^{- μ z}$ on the plane $z = const$ and the potential $ϕ (x, y)= I^{s c} (x, y)$ created by it in this plane.

In case of a uniform distribution of the initial flux over cross-section having the circular form with radius $a$ ,

$σ (r)= \{\begin{array}{l} σ_{0}, & r < a; \\ 0, & r > 0, \end{array}$

and

$ϕ (r)= \int_{0}^{a} \int_{0}^{2 π} \frac{σ_{0} r^{'} d r^{'} d ϑ}{\sqrt{r^{2} + {r^{'}}^{2} - 2 r r^{'} c o s ϑ}} .$

Integration with respect to $r^{'}$ yields

$\begin{array}{l} ϕ (r) = 2 σ_{0} \int_{0}^{π} (\sqrt{r^{2} + a^{2} - 2 r a c o s ϑ} - r + \\ + r c o s ϑ ln \frac{a - r c o s ϑ + \sqrt{r^{2} + a^{2} - 2 r a c o s ϑ}}{r (1 - c o s ϑ)}) d ϑ . \end{array}$

Further, introducing

$χ = \frac{π - ϑ}{2}$

and integrating the term with logarithm by parts, we obtain

$ϕ (r) = 2 σ_{0} [(a + r) E (k) + (a - r) K (k)], k = \frac{2 \sqrt{r a}}{r + a},$ (32)

where $K$ and $E$ stand for total elliptic integrals of the first and second kind respectively. At $r = 0$ , $E = K = \frac{π}{2}$ and Eq. (32) becomes $ϕ (0) = 2 {πaσ}_{0}$ .

In the general case of an axially symmetrical initial profile, the halo $ϕ (r)$ Is expressed via integral

$ϕ (r)= \int_{0}^{\infty} \int_{0}^{2 π} \frac{σ (r^{'}) r^{'} d r^{'} d ϑ}{\sqrt{r^{2} - {r^{'}}^{2} - 2 r r^{'} c o s ϑ}} .$ (33)

Expanding inverse distance with respect to Legendre polynomials,

$\frac{1}{\sqrt{r^{2} + {r^{'}}^{2} - 2 r r^{'} c o s ϑ}} = \frac{1}{r_{>}} \sum_{n =0}^{\infty} {(\frac{r_{<}}{r_{>}})}^{n} P_{n} (c o s ϑ)$

and inserting this into (33) yields:

$ϕ (r)= \sum_{n =0}^{\infty} C_{n} [\int_{0}^{r} {(\frac{r^{'}}{r})}^{n + 1} σ (r^{'}) d r^{'} + \int_{r}^{\infty} {(\frac{r}{r^{'}})}^{n} σ (r^{'}) d r^{'}],$

where coefficients

$C_{n} = \int_{0}^{2 π} P_{n} (cosϑ) dϑ = 2 {πP}_{n}^{2} (0)$

are equal to 0 for odd $n$ , and to $2 π {[\frac{1}{2^{n}} (\begin{matrix} n \\ n / 2 \end{matrix})]}^{2}$ for even. Expression (33) can be integrated over the angle directly.