The article analyzes data from interviews and opinions of teachers and students from several local high schools in the mountainous provinces to detect some limitations and difficulties that the students often encounter while learning geometry and presents the results of the research about the application of several programs to support the process of teaching geometry to students in the mountainous regions of Northern Vietnam.¹

Keywords: teaching students, ethnic groups, mountainous area, application of programs in teaching, innovating methods, teaching geometry, mathematics subject

The mountainous region in the Northern Vietnam includes 14 provinces. This territory has a natural area of about 102.900km² (30.7% of the country’s total area), with 32 ethnic groups that totalize about 14.542.000million people, who represent 13% of the total population. The provinces in the Northern Vietnam naturally have hard conditions, cultural diversity and rich identity and a big number of teachers and students belong to ethnic minorities (Table 1). The reality showed the issue that the majority of the students belonging to these groups in the mountainous areas are “afraid” of geometry, therefore the process of searching for rough solutions to improve this is necessary. In the framework of science paired with technology: “The application of information technology to^2,3 teaching math to high school students following activities turned positive”, we deployed some research following this plan:

1. Detect and clarify the cause of all the “barriers” that are usually met by students from the ethnic groups in the mountainous regions in the process of learning geometry.
2. Searching for rough ways to apply programs to the process of teaching math in order to help the students pass those “barriers” so that step by step the results in teaching geometry to the students from the ethnic groups of the mountainous regions are improved (Table 2).

Several difficulties that are usually met by the ethnic minority students in the mountainous areas in the process of studying geometry

In the process of studying math, in general, and geometry, in particular, the ethnic group’s students in the mountainous areas of the north have several limitations. The results of observing and interviewing 42 math teachers in several high schools in localities in the provinces of Ha Giang, Cao Bang, Lao Cai, Lai Chau, and Tuyen Quang showed that the limitations that the students usually meet when they study geometry are various (Table 3).^4–6

A number of results of the application of programs to the teaching of geometry to students from the ethnic groups in the mountainous areas

The application of programs to show the elements of the lesson thoroughly and exactly: The geometry programs, with all their functions allow the people who use them to create basic subjects such as the point, the straight line, the plan and the basic geometrical relationships such as intersected, parallel or perpendicular, from the Euclidian geometry. Moreover, the geometry programs have a system of tools for more effect on newly studied geometrical subjects and relationships. Therefore, the geometry programs allow us to draw and create all the shapes in the geometry curriculum for high school.⁷

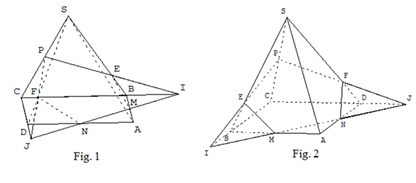
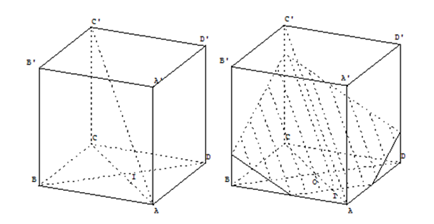
Example 1: With the Geospac W program, after using its functions to draw the face of the pyramid S.ABCD and the plan (MNP) with P, M, N being the midpoints of segments SC, AB, AD respectively (Figure 1) (Figure 2), we easily used the “turn” commands for all the geometrical subjects so that from the position in we switched to the position in Figure 2 to help the students visualize the shape in a better way. With using the “turn” commands the structure of the shape does not change but the students will observe the elements of the given math problem more thoroughly and exactly. Therefore, the program will help the students overcome the issue of drawing the shape incorrectly and will help them understand the typical properties of the drawn shape (to avoid the mistake that the particular features of the drawn shape are the general features of the shape) and also enhancing the ability picturing the space (problems such as dashed lines and continuous lines in the shape; the issue of choosing the best angle of view so that the best visualization is achieved).

Figures 1 & 2 we switched to the position in to help the students visualize the shape in a better way.

Exploiting the element of visualization helps the students detect the elements shown in the drawn shape: In comparison with the shapes in the student’s book, these shapes, especially the moving models created by the program have a few positive roles in the process of teaching math. Instead of sensing the subject directly, the students sense and observe it on a screen (and even detach a part of the shape for a deeper analysis). The use of models in the process of teaching math properly will help the students:

1. Be able to detect the features and characteristics of the subject with a naked eye;
2. Approach abstract notions through specific, simple problems;
3. Develop the capacity to comprehend, especially the capacity to observe, analyze, and synthesize all the phenomena, present all predictions, extract all conclusions that are worth to consider;
4. Establish the correct symbols related to the 3-dimensional shapes, help the students steadily develop their perception of the space.⁸

Moreover, using shapes that were created by the program in advance will save the teacher time in class during each period, giving them more time to organize and coordinate activities to improve the students’ comprehension and checking and marking the students will benefit and will be more efficient.

Figures 3 & 4 Consider math problems 1: Given edges AB, BC of triangle ABC and outside of triangle ABC there are two squares (AB and BC are edges of the squares) with their centers M and N, respectively.

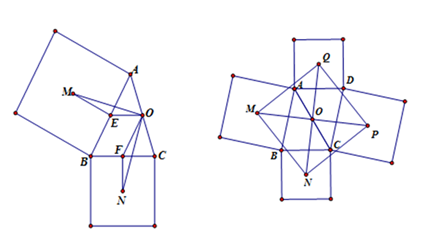
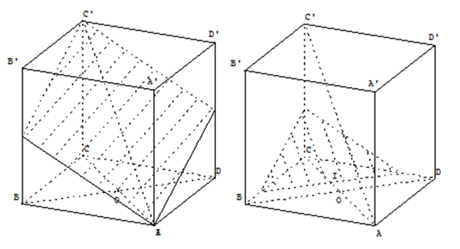
Example 2: Consider math problem 1: Given edges AB, BC of triangle ABC and outside of triangle ABC there are two squares (AB and BC are edges of the squares) with their centers M and N, respectively. With O as the midpoint of segment AC. Prove that triangle OMN is a right-isosceles triangle at O. In the math problem above, the student can easily find the solution as follows: Take E, F as the midpoints of segments AB and BC respectively (Figure 3) (Figure 4). Therefore. From that we deduce,,. And because FO//AB, we deduce. From that we can deduce that. We get DOMN is a right-isosceles triangle at O. Based on math problem 1, we use the functions of the program to create new squares that are symmetrical to the squares that have the centers M and N respectively and that go through point O of segment AC. Take P, Q as centers of these new squares. Now, we have triangles OMN, OPQ that are right-isosceles triangles at O and symmetrical to each other. Because of that we have P, Q as points of symmetry with respect to M, N, so MNPQ is a square. From that we can proceed to problem 2 below:

1. Math problem 2: Given edges AB, BC, CD, DA of the parallelogram ABCD, draw 4 squares outside the parallelogram so that AB, BC, CD, DA are edges of the squares; M, N, P, Q, respectively are centers of the 4 squares. Take point O as the intersection point of the two diagonals of the parallelogram ABCD, so MNPQ is a square. Based on math problem 1, we continue to use the functions of the program; we create squares that are symmetrical with the squares that have the center M and N respectively and that intersect with the axis AC. Their centers are⁹ P, Q (Figure 5) (Figure 6). Then, according to math lesson 1 and to the characteristics of symmetry, we have right-isosceles triangles OMN, OPQ at O and they are symmetrical with each other. Because of that, MQ and NP are parallel, MN=PQ. From that we deduce that MNPQ is a isosceles trapeze. From that we can proceed to problem 3.
2. Math problem 3: Given quadrilateral ABCD, created by 2 identical triangles, ACB and ACD. From AB, BC, CD and DA, create 4squares outside the quadrilateral, so that each of them is an edge of a square. The center points of the squares are M, N, P, Q. Take point O as midpoint of segment AC; MNPQ is a trapeze. Next, using the functions of the program to change the position of point A so that ABCD becomes a rhombus (Figure 6), meaning that we can use the details of math problem 2 or 3 and proceed to problem 4.
3. Math problem 4: Given rhombus ABCD. From AB, BC, CD and DA, create 4squares outside the rhombus, so that each of them is the edge of a square. The center points of the squares are M, N, P, Q. Prove that MNPQ is a square. Based on math problem 1, we apply the results to quadrilateral ABCD 2 times consecutively. Then, we have right-isosceles triangles OMN, OPQ at O. So, we have Q (O; 90⁰): P®Q, M®N. From that we deduce: có Q (O; 90⁰): MP®NQ. So MP=NQ and MP is perpendicular to NQ. Then we proceed to math problem 5.
4. Math problem 5: Given AB, BC, CD, DA of quadrilateral ABCD, draw 4 squares outside the quadrilateral so that each of them is an edge of a square. The center points of the squares are M, N, P, Q, respectively. Prove that MP=NQ and MP is perpendicular to NQ. Based on math problem 5, we make point D matches point C in quadrilateral ABCD (Figure 7) (Figure 8). Then we will have P matching C. Then we will have MC perpendicular to NQ and MC=NQ. And then we will have the result for math problem 6.
5. Math problem 6: Based on the 3 edges AB, BC, CA of triangle ABC, draw 3 squares outside ABC so that each of the them is the edge of a square. Take M, N, P as the center points of the 3 squares with edges AB, BC, CA, respectively. Prove that MC is perpendicular to NQ and MC=NQ. From this examples we can understand that exploiting the visual elements of models on a screen in the process of teaching math helps the students draw shapes accurately (especially multi-dimensional shapes), visualize shapes. Through this, students not only improve their imagination and overcome drawing shapes inaccurately but they also overcome identifying or using concepts and characteristics of geometry incorrectly; recognizing geometrical elements with the naked eye, the relationships between mathematical subjects shown by shapes.

Figures 5 & 6 Given rhombus ABCD. From AB, BC, CD and DA, create 4 squares outside the rhombus, so that each of them is the edge of a square. The center points of the squares are M, N, P, Q. Prove that MNPQ is a square.

Figures 7 & 8 Given AB, BC, CD, DA of quadrilateral ABCD, draw 4 squares outside the quadrilateral so that each of them is an edge of a square. The center points of the squares are M, N, P, Q, respectively. Prove that MP=NQ and MP is perpendicular to NQ.

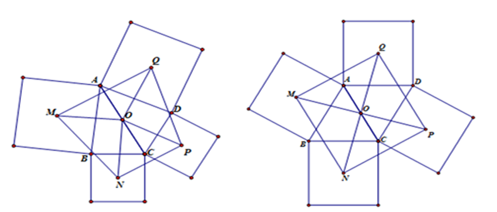
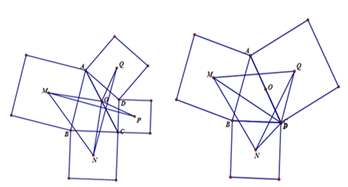
Illustrations of the results of the solution for the math problems

The geometry program with functions of checking measures (measures of angles, length, area) leaves marks of a point, sets up the locus of a point, keeping the structure of a shape intact when the elements of the lesson change has helped the students see the figures of the results of the lesson and the results of the lesson in special cases. More than that, through the visual images that the program shows, we can create new math problems starting from the first problem.

Example 3: Given parallelepiped ABCDA’B’C’D’. Take point I on segment AB. Determine the face created by the parallelepiped and plane (α) that goes through I and is parallel with BD and AC’. In order to help the students solve this problem, the teacher can introduce the GeospacW program as explained below:

1. Activity 1: Understanding the math problem
   Teacher: Open file VD3. g3W (Figure 9) (Figure 10) so that the students can observe the shape, determine the given elements, observe the figures of the face when point I changes to extract the characteristics of the face. Students: Observe the shape on the screen, determine the elements at the beginning; observe the figures of the face on the screen and predict the set up.
2. Activity 2: Building the plan for solving the math problem.
   Teacher: Use the tool “Historique” to show all the geometrical subjects following their sequence, one by one. Students: Start drawing the shape; compare each step of creating the shape as the teacher instructed so that any possible errors are noticed in time.
3. Activity 3: The demonstration.
   Teacher: Require the students to repeat all the ways to prove that a plane is parallel with a straight line in space.
   Students: Use the general methods to prove that the face that goes through I is parallel with the two straight lines BD and AC’.
4. Activity 4: Examine the solution.
   Teacher: Transform the shape (so that the students can detect the special positions of point I and the face in all those situations).
   Students: Observe and comment:
   1. When I is on segment AO (ignore A and O) the face is a triangle.
   2. When I coincides with a then the face is a rectangle.
   3. When I belongs to OC (ignore C) the face is a triangle (Figure 11) (Figure 12).

This example shows us again that the application of information technology to teaching geometry in a proper way helps students overcome the difficulties in drawing shapes, especially drawing the shapes that appear in three-dimensional shapes. Moreover, all the tools of the program will support the students in counting and checking the relationship between all subjects in order to recognize the relationship between all mathematical subjects that are shown in the drawn shape. With all the results that the program will notify, students will compare to check the results of their solutions or go back to find the solution, and the method of solving the math problem.

Figures 9 & 10 Open file VD3. g3W so that the students can observe the shape, determine the given elements, observe the figures of the face when point I changes to extract the characteristics of the face.

Figures 11 & 12 When I coincide with A then the face is a rectangle When I belong to OC (ignore C) the face is a triangle.

Pioneering the moving elements of the models on the computer help the students understand the process of thinking

With the “moving” functions and with preserving the structure of the programs used for teaching, teachers as well as students can change the angle of approach of the models so that students can detect the characteristics of math, all the mathematical relationships such as the change of math subjects when watched with a naked eye. Even more, we can change some subjects in these models so that students can observe the corresponding change of the remaining subjects in these mathematical models, and from that to detect the connections between different subjects, and quantities in these models. Using these programs in teaching and using information technology in general to help students search and explore all the attributes in these models will create a favorable environment for the students to have the conditions to develop their ability to deduce in math and their ability to think logically and especially the ability to observe, analyze, compare and predict…for their own benefit.¹⁰

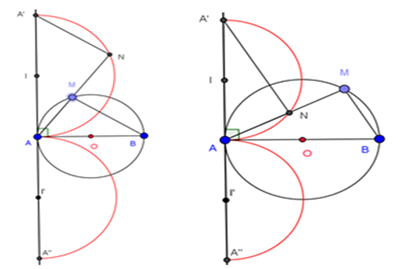
Example 4: Take a semicircle with diameter AB. Point M is mobile on the semicircle. Point N is on ray AM so that $AN=\frac{BM}{2}$ . Find the locus of N in each given position of M on the semicircle. We can use Geogebra to exploit the math problem as it follows: Understanding the content of the lesson (Table 4) (Table 5).

Figures 13 Take a semicircle with diameter AB. Point M is mobile on the semicircle.

Figures 14 & 15 Use Geogebra to create marks for point N, change the position of point M so that the students observe the locus.

1. Activity 1: Effectuating the solution

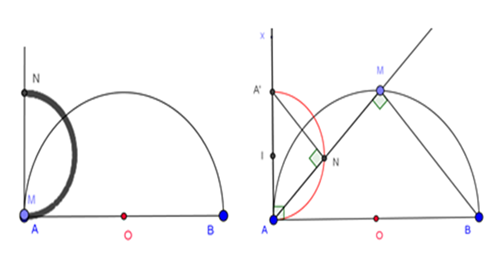
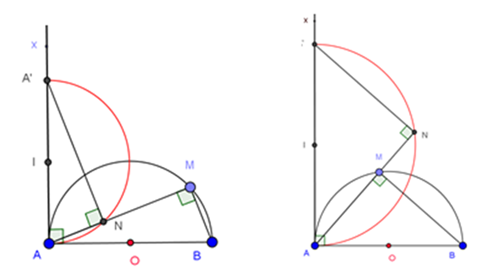
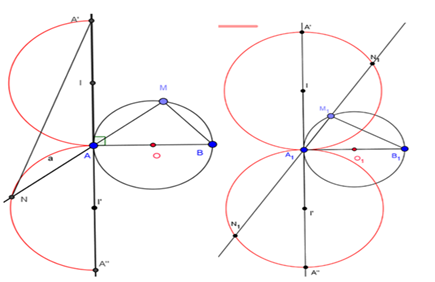
Draw ray Ax that makes a right angle with AB as drawn in Figure 16. On ray Ax, take point A’ so that AA’ =$\frac{1}{2}$ AB. Therefore, we have A and A’ fixed. Because AN = $\frac{1}{2}$ BM, AA’ = $\frac{1}{2}$ AB and triangles A’AN = ABM, it means ABM ~A’AN We deduce that $\widehat{A\text{'}NA}$ =$\widehat{AMB}$ = 90^o. Therefore, N is on the semicircle with diameter AA’. Because M is moving on the semicircle with diameter AB, ray AM is limited by rays AB and Ax. Because of that, N Î AM only move on semicircle with diameter AA’ which belongs to the plane with AB, which contains the given semicircle. So the locus of point N is semicircle with diameter AA’ which belongs to the plane with AB, which contains the given semicircle (Figure 16) (Figure 17).

2. Activity 2: Research the solution thoroughly

Research and exploit the math problem thoroughly by considering special situations, similar cases, generalization. We have a few math problems below:

1. he 1st way: Based on the original problem we change the assumption that point N is on ray AM so that AN=$\frac{1}{2}$ BM with the assumption that AN=BM, in this case we have the result of Math problem 1. Consider semicircle with diameter AB. Point M is mobile on that semicircle. Take point N on ray AM so that AN=BM. Find the locus of point N when M changes. With the help of Geogebra, we can easily find the result of this problem such as illustrated.
2. The 2nd way: Based on the original problem and problem 1, generalize the assumption that AN=BM and AN=BM so that AN=k.BM and then we have the results of Math problem 2. Take semicircle with diameter AB. Point M is mobile in that semicircle, k is a positive number. Take point N on ray AM so that AN=k.BM. Find the locus of point N when M changes. With the help of Geogebra, we can easily find the results for the problem as shown in Figure 16 &17).
3. The 3rd way: We change the information that AB is the diameter of a semicircle, from problem 1, with the assumption that AB is the diameter of a circle, and so we get the results of Math problem 3: Consider a circle with AB as its diameter. Point M is moving on that circle. Take point N on segment AM so that AN = BM. Find the locus of point N when M changes. With the help of the Geogebra program, we easily find the result for this problem (Figure 18) (Figure 19).
4. The 4th way: We change the information that AB is the diameter of a semicircle, from problem 2, with the assumption that AB is the diameter of a circle, and then we have the results or Math problem 4: Consider a circle with AB as its diameter. Point M is moving on the circle, k is positive number. Take point N on ray AM so that AN=k.BM. Find the locus of point N when M changes. With the help of the Geogebra program, we easily find the result for this problem, as shown in.^11,12
5. The 5th way: We change the assumption that N is a point on segment AM so that AN=k.BM, from problem 4, with the assumption that N is on a segment opposite segment AM so that AN=k.BM and we have the results for Math problem 5: Consider a circle with AB as its diameter. M is a moving point on the circle, k is a positive number. Take point N on a ray MA so that AN=k.BM. Find the locus of point N when M changes. With the help of the Geogebra program, we easily find the result for this problem, as shown in (Figure 20 & 21).
6. The 6th way: We change the assumption that N is a point on a segment opposite segment AM so that AN=k.BM, from problem 5, with the assumption that point N is on straight line AM so that AN=k.BM and we have the results of Math problem 6: Consider a circle with AB as its diameter. Take M as a moving point on that circle, k is a positive number. Take point N on line AM so that AN=k.BM. Find the locus of point N when M changes. With the help of the Geogebra program, we easily find the result for this problem, as shown in Figure 21. Through this example we can see that the application of information technology in teaching math, besides the fact that it helps students to overcome the difficulties of drawing shapes, it also aids them in calculating and in checking the relationships between different subjects and more than that, it helps students to consolidate their knowledge. With the use of different ways influence the mind so that new math problems are created from the original one, students have the chance to develop their thinking (specialization, generalization), ability to figures space in their minds and also to develop their ability to change the language they use.

Figures 16 & 17 Draw ray Ax that makes a right angle with AB, with the help of Geogebra, we can easily find the results for the problem.

Figures 18 & 19 With the help of the Geogebra program, we easily find the result for this problem, with the help of the Geogebra program; we easily find the result for this problem.

Figures 20 & 21 With the help of the Geogebra program, we easily find the result for this problem, with the help of the Geogebra program; we easily find the result for this problem.

Assessing the results the application of programs to teaching geometry

From all research, we put together the data of pedagogical experiments to give a correct assessment about the effect of the application of programs to teaching geometry to students from ethnic groups, in the mountains: The teachers’ assessment: We interviewed 42 teachers that took part in the pedagogical experiment; the results are:

+ 40/42 teachers agree that: The application of information technology in the process of teaching geometry made students attracted to studying and created an exciting atmosphere in class; students can understand the lesson in class; Allowing students to work in groups and use the programs had a good effect, helping students to detect the relationships between the hidden mathematical subjects in the problems’ assumptions.

+ 40/42 teachers agreed: The geometry programs helped to teach geometry very well and had no negative influence in training the students how to draw geometrical shapes.

+ 40/42 teacher stated: The use of program in teaching geometry helped students notice the relationships between mathematical subjects, overcome their mistakes when drawing shapes geometrical shapes, and helped them calculate accurately and fast.

+ 36/42 teachers assessed: The exploitation of programs in the process of teaching helped students understand clearly and consolidate their knowledge. With all their functions, to create a shape, to measure, to check…, the geometry programs helped teachers to easily show different situations with mathematical visual models so that students could proceed with activities of identifying and showing some knowledge learned before.

+ 37/42 teachers stated: The use of geometry programs with options of moving subjects in class helped students develop their ability to think and to figures space in their minds. With the function of preserving the structure of a shape when changing a few assumptions from the beginning (following the specialization way) of the geometry program, students easily understood the results of the problem in some special cases (like example 3 above). Besides, understanding the results of the math problem, students can handle similar operations the generalization, with the help of the program and can easily get similar results or create new math problems by changing assumptions in these problems (following the generalization way) (like example 4 above).

- The students’ assessment: We interviewed 307 students that took part in this pedagogical experiment; the results are:

+ 303/307 students stated: The use of computers and geometry programs in class created effective classes; students liked the activities that involved computers during classes and participated very enthusiastically.

+ 307/307 students stated: When using information technology, in general, and geometry programs, in particular, in teaching geometry, students understand the lesson and are able to use their knowledge to solve the problem better, limit their mistakes that they usually make in the process of using their knowledge when solving a problem.

+ 289/307 students stated: The use, by the teacher, of programs in the process of teaching geometry helped students draw shapes more accurately, visualize better, limit their mistakes when creating shapes.

+ 305/307 students stated: The use, by the teacher, of the geometry programs with options of moving subjects while instructing students how to solve a problem helped students easily detect the relationships between mathematical subjects, and then helped students develop their ability to think for themselves.

It can be said that teaching geometry with the said of information technology made activities become beneficial and students from ethnic groups absorbed knowledge easily and actively. Through all the lessons with the aid of information technology, students from ethnic groups from the mountainous regions of Vietnam not only get to train their drawing geometrical shapes skills, and have the conditions to get more knowledge but also limit and overcome the mistakes that they usually make when solving math problems.

The results of inquiry showed certain limits in the ability to think and some mistakes that are usually encountered in the process of teaching geometry to students from the mountainous regions of Northern Vietnam. To overcome the difficulties in studying geometry, that students from ethnic groups in the mountainous areas usually meet, the application of programs to teaching geometry offered visualizations that helped students detect the relationships between different elements of different shapes, hidden in the models, and from that detect and give solutions to math problems through cooperation, therefore contributing to the process of thinking. The results of the two groups, the students that studied geometry aided by computers and the students that studied geometry without computers show that number of mistakes of the students from the 1st group has decreased in comparison with that of the students from the 2nd group. The capacity of solving math problems, cooperating, detecting and solving problems and using a computer program of the students from the 1st group has increased a lot, in comparison to the students from the 2nd group.

None.

Authors declare that there is no conflict of interest.

1. Trinh Thanh Hai, Tran Viet Cuong. Designing and exploiting mobile models on screen in teaching math in high schools. Journal of Teacher Education. 2014;60(1):40–43.
2. Trinh Thanh Hai, Trinh Thi Phuong Thao. Exploiting the visual properties and the mobile properties of geometry programs with options of moving subjects to help students from ethnic groups, mountainous areasto solve geometry problems. The Journal of Education. 2015;372:32–34.
3. Trinh Thanh Hai, Tran Viet Cuong, Trinh Thi Phuong Thao. Textbook for using IT in teaching math. Vietnam Education Publishing House, Vietanam; 2013.
4. Marilyn Leask. Issues in Teaching using ICT, Routledge Falmer, London. Journal of Computers & Education. 2001;40(2):194–195.
5. Sue Johnston Wilder, David Pimm. Teaching Secondary Mathematics with ICT. MPG Books Ltd. Bodmin, Cornwall, Great Britain, UK; 2004. p. 1–273.
6. Haji Razali bin Ahmad. Constructive Teaching and Learning by information Technology. Malaysia; 2004.
7. Roy Barton. Learning and Teaching Secondary Science with ICT, MPG Books Ltd, Bodmin, Cornwall, Great Britain, UK; 2003.
8. Mary Hayes, David Whitebread. ICT in the Early Years. OZGraf SA, Poland; 2006. p. 1–20.
9. Michael D Devilliers. Rethinking proof with The Geometer’s Sketchpad, Key Curriculum Press, Vietnam; 2003;36:72.
10. Dan Bennett. Exploring Geometry with The Geometer’s Sketchpad. Key Curriculum Press, Vietnam; 2002. p. 360.
11. Trinh Thanh Hai, Tran Trung Tinh. Building Capacity Framework of Mathematics Teacher in Assessment of High School Students in Vietnam. Annals. Computer Science Series Tome, Romania; 2017.
12. Tran Viet Cuong. Organizing Project Based Teaching in the Training of Math Teachers in Vietnam. Revista Romaneasca pentru Educatie Multidimensionala. 2017;9(2):1–4.