Agar (Aquilaria malaccensis Lamk, Family- Thymeleaceae) has drawn unique position due to the production of world’s most expensive essential oil used in fragrances and as medicine. It is one of the most valuable and economically important commercial tree species planted in some potential forest areas of Bangladesh. The growth rate and yield of the species in Bangladesh are not known. Therefore, for scientific management of the forest necessity of the growth and yield models for the species were felt. The present study was made to derive mathematical models for growth and yield of this species in Bangladesh based on site indices. The models were developed through establishment of permanent sample plots (PSPs) and temporary sample plots (TSPs) with area 0.02 ha and shape is circular and rectangular. Diameter at breast height and total height of all trees in the plots were measured for four successive years from PSPs. Step-wise method and all probable combinations of the independent variables method were used to select the best suited models subject to the satisfaction of the statistical and biological requirements. Models were selected to estimate the stand stocking, stand height, stand diameter, stand basal area and stand volume yield per hectare. The yield prediction models derived in the study could satisfactorily be used for Agar tree plantations within stand age of 3.5 to 17.5 years and site indices of 8. To 20.0 meters based on a base age of 12 years.

Keywords: aquilaria malaccensis lamk, Bangladesh, growth and yield, mathematical, models

The elements of growth and yield models are the known and measurable changes, which are assessed using biological theories relevant to living systems and mathematical language. Biological theories and mathematical language help in isolating either individually or in combination the complex tree interactions that are hard to verify, and a logical relationship is then assumed in simulation of growth and yield of a forest tree or stand. Forest growth models attempt to quantify the growth of a forest, and are commonly used for two principal purposes: to predict the future status of a forest and the nature of any harvests from that forest, and to help consider alternative cultivation practices. Models may also find other uses, such as in education, communicating information, etc. Depending on the purpose of the model, modelers may choose to emphasize physiological detail or statistical efficiency, but generally seek both biological and statistical accuracy.

Several decisions regarding forest management depend on the growth and yield of the growing stocks. Yield estimation provides information of a particular forest stand at a specified age. This enables decision makers to formulate forest regulation activities and determine timber liquidation schedules. Furthermore, information is required to evaluate the alternate to economic management of the forest: that of determining the appropriate rotation age of the forest. The growth and yield information can also be used to determine the performances of forest stand as sources of basic information. Hence, the prediction of growth and yield will serve as direct input of the other components of the system especially in the plantations in Bangladesh. The object of this study is to develop a mathematical model for growth and yield estimation of Agar (Aquilaria malaccensis Lamk) plantations in Bangladesh.

Aquilaria malaccensis is the most widespread species of the Aquilaria genus found in Bangladesh, Bhutan, northeast India, Sumatra and Kalimantan of Indonesia, Iran, Malaysia, Myanmar, southern Philippines, Singapore and southern Thailand.¹ It is the most highly valuable non-timber products harvested from tropical forests and used in the manufacture of perfume, incense, traditional medicine, and other commercial products by Muslims and Asian Buddhists.² The aromatic resin known locally as ‘agar’ yield an essential oil that is a key perfume ingredient through distillation, meanwhile, incense are commonly processed from distillation residues and lesser quality material. A. malaccensis Lamk is a major producer of agarwood in Bangladesh for international trade. In Bangladesh A. malaccensis Lamk, is found in the eastern hill regions in the divisions of Sylhet, Chattogram, Chattogram Hill tract and Cox’s Bazar. A. malaccensis Lamk is known to be one of the most important species of commerce and valued for production of its impregnated resinous heart wood that gives fragrance. The infected parts of agarwood serve as important raw material in the production of incense, perfumes and traditional medicines.³ The agar wood oil or aloe wood oil, known in the east as ‘agar attar’ is obtained by distilling selected parts of the infected wood of Aquilaria sp. which has unique fragrance and high export value. The agar oil traders have to sacrifice whole tree as its heart wood serves as raw materials for oil distillation. Many uninfected or less infected trees are also been destroyed by them in search of agarwood. Many studies have reported a reduction in the natural populations of A. malaccensis Lamk due to the high demand of agarwood. As a result, this species is classified as ‘vulnerable’ by the International Union for the Conservation of Nature.⁴ Sustainable agarwood production to support socioeconomic development and conservation of the species in its natural habitat is possible only through domestication of the wild species.⁵

The growth & yield and determination of optimal harvest age of the species has not yet been determined systematically. But, these information are necessary for scientific management of the plantations. The growth information of this species is not adequate and cannot be used to develop any age-growth equation. Therefore, the present study have been completed to generate scientific data for the forecast growth and yield of Agar (Aquilaria malaccensis Lamk.) based on site indices.

Study area

The Forest Department of Bangladesh has taken an initiative to expand and popularize agar plantation in the country considering the economic value of such a unique forest resource, particularly for its demand in the international market. They cultivated Agar tree under agar plantation project in many potential places in Sylhet, Chattogram, Cox's Bazar and the districts of Chattogram Hill Tracts. The study was conducted in the remnant the existence agar plantation in several forest beat of these forest areas (Figure 1). The Permanent Sample Plots (PSPs) and Temporary Sample Plots (TSP) were taken from the plantations raised by these forest division.

Figure 1 Location of study area.

Data for growth models

The number of plantations of Agar (Aquilaria malaccensis Lamk.) in Bangladesh were large scale and have available age groups with spacing are 1.8 × 1.8 m and 2.0 × 2.0 m. Data have been collected though establishment PSPs and TSPs from available agar plantations in studied areas for development of growth and yield models. For each age classes the plantations were selected at random and then three Permanent Sample Plots (PSP) from each plantations were selected for measurements. Data have been collected from PSPs consecutive four year. Circular and rectangular plots were taken of area 0.02 hectare each. More than 35 PSPs were established in studied areas for the study (Table 1). All the trees in a plot were marked for diameter measurement at breast height (Dbh) (1.3 m) with red paint and numbered. Dbh and height of all the trees in the plot were measured by diameter tapes and Haga altimeter respectively for successive 4 years.

The number of permanent sample plots was not enough to predict the growth and yield of the species. Therefore, TSPs were laid out in the available existing plantations of studied areas in Bangladesh. More than 232 TSPs were laid out for the study (Table 1). Ranges with plantations having maximum age ranges were selected. From each plantation at least three plots were selected at random. The plots were rectangular or circular of 0.02 ha each. The diameters at breast height (Dbh) of all trees in a plot were measured by using diameter tape. The heights of the tallest two trees (100 trees per hectare) per plot were measured by height measuring instrument as dominant height. The heights of other trees were estimated by comparing the heights of the trees measured. The Dbh and height of all trees in plots have been entered into the computer.

Data collation

For statistical processing, information were derived for stand age (A), mean stand Dbh, average dominant height (H), average stand height (Mht), basal area per hectare (BAha^-1), total volume (V_tha^-1) and site index. Average number of stem per hectare (Nha^-1) at each age group were also determined. The volume of the individual tree was estimated by using the volume equation for the species developed by Islam and Chowdhury¹² of the form:

$V_{o}b=-0.097547+0.009443\times D+0.001784\times H+0.000017\times D^2\times H$

$R^2=0.97andN=250$

For determination of growth and yield equations, the site index calculation by the site index equation developed by Islam et.al.⁶ with reference age is 12 year which is of the form:

$ln(S)=ln(H)+\frac{6.05801}{A^1{}^{.1}}-0.39376,$  $R^2=0.93andN=372$

Predictions of growth and yield

The following equation were tested for best suited growth and yield prediction models

Stand stocking equation

$Nh{a}^{(-1)}=f(A)$

Stand total mean height equation

$Mht=f(A,SI,Nh{a}^{(-1)})$

Stand diameter at breast height equation

$Dbh=f(A,SI,Nh{a}^{(-1)})$

Stand basal area equation

$Bah{a}^{(-1)}=f(A,SI,Nh{a}^{(-1)})$

Stand Yield Equation

$V_{t}h{a}^{(-1)}=f(A,SI,Nh{a}^{(-1)})$

Where:   SI is the Site index

Mht is the total mean height of the tree,

Dbh is the diameter at breast height of the tree

Ba ha^-1 is the basal area of tree per hectare

V_t ha^-1 is total volume of the tree per hectare

A is the Age in year

For determination of the best suited growth and yield models, the site index model were used developed by Islam⁶ This was followed by derivation of stand mean diameter at breast height (Dbh), stand mean height (Mht), stand basal area per hectare (Ba ha^-1), stand volume per hectare (V_t ha^-1) yield models. The independent variables of the stand yield prediction models were age, site index & stand stocking and the dependent variable was Dbh, Mht, Ba ha^-1 and (V_t ha^-1). One model to estimate the numbers of trees per hectare at different ages were also derived. Step-wise and all probable combinations of the independent variables regression methods were used to select the best suited models subject to the satisfaction of the statistical and biological requirements. Different transformations of the variables either in the form of natural logarithm (ln), reciprocal or combining two variables in the transformed or in the original forms or combinations along with the original variables were used for regression analyses. Stepwise regression analysis was done to derive the best suited prediction models. All possible regressions were worked out by taking ln as dependent variable. Independent variables in the form of 1/ S, ln(S), 1/ ln(S) for site index and 1/A, ln(A) and S/A for age were used. Two-stage least squares method was used to choose desired equation out of the different combinations. In this way, equations for stand mean height, stand Dbh, stand basal area per hectare and volume per hectare were derived. The stand variable presented in the Table 2.

Model performance criteria

The selection of appropriate criteria to assess the model performance is a critical consideration. There is no single criterion for selecting the best regression model from among a number of models.⁷ Using multiple measurements of performance instead of single measurements is a common and more objective approach.⁷

The most commonly used criteria to evaluate the model performance are the coefficient of determination (R²). The R-squared (R²) statistic measures the success of the regression in predicting the values of the dependent variable within the sample. In standard settings, may be interpreted as the fraction of the variance of the dependent variable explained by the independent variables. The statistic will very closed to one the regression fits perfectly. The R-squared (R²) measured as:

$R^2=1-\frac{{\displaystyle \sum _i{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle \sum _i{\left({\widehat{y}}_i-{\overline{y}}_i\right)}^2}}$

The root mean square error (RMSE) is a well-accepted goodness-of-fit indicator describing the difference in observed and predicted values in the appropriate units with lowest value.⁷ RMSE is defined as follows:

$RMSE=\sqrt{\frac{{\displaystyle \sum _i{\left(y_i-{\widehat{y}}_i\right)}^2}}{N}}$

where, where $y_i$  and ${\widehat{y}}_i$  are the original data values and modeled (predicted) values respectively and mean of original data. N is the number of pairs of values.

Model validation

Statistical validation

Statistical validation was the first step done in validating the models. It included the analysis of variance minimum residual mean square, the highest coefficient of determination (R²) and the highest adjusted R² with lowest RMSE.

Independent test

Validation of the chosen models of stand height for agar tree was done by using data from 30 separate sample plots. This was done by comparing the estimated and observed values, applying the chi-square test of goodness of fit, paired t-test and percent absolute deviation (%AD). This was also compared with 45 degree line test by plotting the observed values and the predicated value in the graph.

Biological principle testing

For biological principle testing, predicted Stand mean height, stand Dbh, stand basal area per hectare and total volume yield per hectare derived from the chosen models were plotted against age for different site indices. The yield curves should be of sigmoid shape and asymptotic to the carrying capacity of the site.^8–11

The selected stem per hectare (Nha^-1) prediction equation, stand mean height (Mht) equation, stand diameter at breast height (Dbh) growth equation, stand density or stand basal area (Baha^-1) in square meters per hectare prediction equation, stand volume cubic meters per hectare prediction equations are stated in Table 3 below along with the corresponding coefficient of determination and root square mean error.

The highly significant regression coefficients of predicted the stand stoking, stand mean height, stand diameter at breast height, stand basal area per hectare and volume yield per hectare models are 0.86, 0.96, 0.90, 0.88 and 0.78 respectively. These reveal that predicted stem per hectare is highly correlated with independent variable age (A). The stand mean height, stand diameter at breast height, stand basal area per hectare and volume yield per hectare are highly correlated with independent variable age (A), site index (SI) and number stocking (N). These also indicate that stand stoking, stand mean height, stand diameter at breast height, stand basal area and volume yield models explain 86%, 96%, 90% , 88% and 78% of the total variation respectively at Significant level of. Standard error of 4 numbers of stem per hectare, 0.07 meters of stand mean height per tree, 0.13 centimeters of Dbh per tree, 0.26 square meters of stand basal area per hectare and 0.44 cubic meters of stand volume yield per hectare for Agar tree (Aquilaria malaccensis Lamk) showed reasonably low value indicating best fitting of the models. The indicative prediction curves given in Figure 2.

Statistical validation and biological principle testing

The selected models satisfied all the statistical criteria. The predicted values were plotted against ages for different site indices (Figure 2). The curves found to confirm with the ideal attributes of a biological yield curves. The yield curves were sigmoid. The yield curves also showed that at a given stand age, higher yield is expected on better sites.

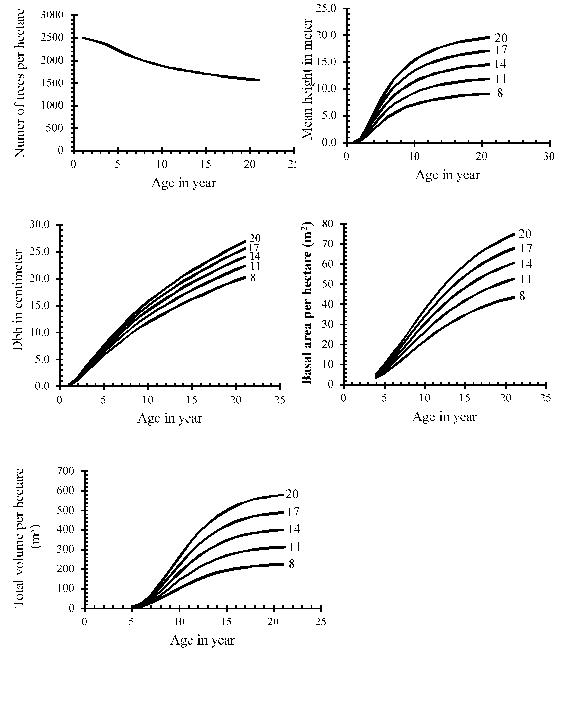
Figure 2 Predicted growth and yield curves of Agar (Aquilaria malaccensis Lamk.) plantations in Bangladesh.

Independent test

The computed chi-square, t-value, absolute deviation present (%AD) and slope for number of tree per ha., mean height, diameter at breast height, basal area and volume yields are given in Table 4. The computed chi-square and t-vales were less than the tabular values  and. These imply that there is no significant difference between the actual values form the 30 test sample plots and the corresponding expected values as predicted by the models. Hence, the selected models confirm with the set of data.

45 degree line test

Graphs comparing the observed values and the predicted values were plotted in the graph paper. It was observed that the models tend to make an angle of 45 degree with the axes meaning there is no significant difference between actual and predicted values Table 4.

This study embodies details of growth and yield models of Agar (Aquilaria malaccensis Lamk) plantations in Bangladesh. The predicted models are composed of following five equations: stand stoking equation, stand mean height equation, stand dominant height equation, diameter growth equation, stand density equation and stand volume yield equation. These equations will predict stand number of tree (stoking) per hectare, stand mean height, stand dominant height, stand diameter at breast height, stand basal area (density) per hectare and stand volume per hectare at different sites. Forest users will readily get values from the tables generated by the predicted models of these parameter as desired rather than calculating them for general use. If the users know the age and site indices of given stand of Agar (Aquilaria malaccensis Lamk), it will be easy and safe for them to estimate the growth and yield variables by using the models given in this study. The predicted models can be used for trees, the ages of which are within 3.5 to 17.5 year and site indices of 8.0 to 20.0 meters based on a base age of 12 years. Extrapolation over this data range is not recommended.

The author feels that the sample plots covering the range of site variation and stand history are necessary for given forest type or plantation species for the development of a standard model equation. But in this study it could not be achieved due to limitations in time allotted for the study and other necessary factor. To develop growth and yield models thought establishment of PSPs it is needed more than ten years of successive data sets. Moreover, the plantation of Agar (Aquilaria malaccensis Lamk) in the country so widely scattered that it was not possible to cover equally poor sites, average sites, good sites, low density stand, average density stand, high density stand, old logged stands, stands at mid-rotation or midway through felling cycle and stands at rotation age or at the end of the felling cycle, which are necessary for the development of an ideal model. All age classes of the Agar (Aquilaria malaccensis Lamk) were also not available in the study area. Other than these no conventional thinning was done in the studied plantations. As a result, some irregularities were observed in the analysis of collected data. The models may be improved by using data collected from a wide range of variation in stocking (number of stem per unit area) for exploring independent variables to get more precise estimate.

In this study, growth and models were developed for Agar (A. malaccensis Lamk) planted in Bangladesh by site index guide equation. All growth and models contribute significantly to improving our knowledge Agar tree growth in Bangladesh. Moreover, this is the first study for Agar tree of its growth and yield models in Bangladesh.¹²

The main goal of this study was to measure the growth and yield of Agar (Aquilaria malaccensis Lamk) using different selective appropriate method for their possible application in growth and yield simulators and basic calculations of forest inventories in Bangladesh. Thus, the model predictors used are variables typically measured in forest inventories. The inventory data that was gathered during the field inventory was suitable for constructing these models. In this study the total volume of Agar tree have been predicted by the developed by Islam and Chowdhury¹² and site index been predicted with a model by Islam et.al.⁶ was regarded as an absolute true value for individual-tree volume and site index. Growth and yield prediction models were developed in the present study for supporting sustainable management of the Agar tree forest in Bangladesh. Most statistical and biological tests of models presented showed adequate prediction accuracies. The models of this study performed well in independent test data and were consistent with the forest growth theory. The growth models can be used in Bangladesh in forest planning calculations to evaluate the site quality and for estimating the yield of a stand at a certain moment.

None.

The author declares there is no conflict of interest.

1. Lee SY, Mohamed R. The Origin and Domestication of Aquilaria, an Important Agarwood-Producing Genus. In: Mohamed R. editor. Agarwood: Science Behind the Fragrance, Springer. 2016.
2. Turjaman M, Santoso E, Sumarna Y. Arbuscural mycorrhizal fungi increased early growth of Gaharu wood of Aquilaria malaccensis and A. crasna under greenhouse conditions. J For Res. 2006;2:139–148.
3. Beek, Heuveling van H, Phillips D. Agarwood: Trade and CITES mplementation in Southeast Asia. Unpublished report prepared for TRAFFIC Southeast Asia, Malaysia. 1995. p. 1–60.
4. Anonymous. International Union for the Conservation of Nature (IUCN): Red list of threatened species. IUCN, Gland. 2002.
5. Kumar BM. Home garden-based indigenous fruit tree production in peninsular India. In: Akinnifesi FK, et al., editors. Indigenous Fruit Trees in the Tropics: Domestication, Utilization and commercialization. CAB International Publishing, Wallingford, UK, 2008. p. 84–99.
6. Islam SMZ, Chowdhury MA, Misbahuzzaman K. Mathematical Models for Estimating Tree Site Index for Agar tree(Aquilaria malaccensis Lamk) Plantations in Bangladesh. Indian Forester. 2018;144 (12):1172–1178.
7. Aertsen W, Kint V, Van Orshoven J, et al. Comparison and ranking of different modeling techniques for prediction of site index in Mediterranean mountain forests. Ecological Modelling. 2010;221(8):1119–1130.
8. Latif MA, Das S, Rahman MF. Growth and yield tables for Acacia mangium grown in the plantations in Bangladesh. Journal of Tropical Forest Science. 1997;7(4):591–598.
9. Latif MA. Estimation of site index of teli garjan (Dipterocarpus turbinatus gaertn. F.) in Bangladesh. Bangladesh Journal of Forest Science. 1999;28(1):54–48.
10. Newaz MS, Mustafa MM. Growth and yield prediction models for Acacia mangium grown in the plantations of the central region of Bangladesh. Kluwer Academic Publishers, Netherlands. New Forests. 2004;27:81–88.
11. Islam SMZ. Mathematical Model of Growth and Yield of Swietenis macrophyla King (Mahogany) Planted in Bangladesh. M. Phil thesis. Research Centre for Mathematical Physical Science (RCMPS), University of Chittagong. 2006.
12. Islam SMZ, Chowdhury MA. Equation for Estimating Stem Volume for Agar tree (Aquilaria malaccensis Lamk) Grown in the Plantations in Bangladesh. Journal of Tropical Forestry and Environment. 2017;7(2):91–101.