In our study a sandwich composite beam under three point bending is considered. The core material of the beam contains an initially small crack oriented parallel to the longitudinal axis and very close to the upper skin interface. A code using commercial finite element software has been developed in order to predict the position, the length of the crack and the direction where kinking occurs inside the core of the sandwich beam. The code uses the energy criterion, and the code control points of decision concerning the propagation and the kinking of the crack are based on energy formulas from the fracture mechanics approach. A general flowchart of the proposed code and results from the critical crack length– kinking into the core, are presented.

Keywords: sandwich beam, fracture mechanics, j–integral criterion, finite element analysis, composite materials

Composite materials utilizing the sandwich structure are a basic family of materials and possess a highly increasing use in modern industrial applications. Since the traditional approach to structural design and material selection tends to be replaced by the Fracture mechanics approach, it is worth understanding the way that the Fracture mechanics approach is applied. The traditional approach to structural design takes into account two variables which have to be in contrast: The applied or expected stresses and the Yield or Tensile strength. The Fracture mechanics approach^1,2 involves three important variables rather than two. The additional structural variable is the flaw size, and the Fracture Toughness replaces Yield or Tensile strength. This approach quantifies the critical combination of these three variables. In Fracture Mechanics there are two methods of studying a problem, the Stress Intensity Factors criterion and the Energy criterion. In this study we get involved with the Energy criterion and specifically with the J Contour integral calculation.^3-5

A sandwich material consists of a core material with thin laminas on each side.⁶ The laminas could be any combination of fibers and matrices, or even of a metallic material. The core is usually made of PVC, wood or a honeycomb material. The most interesting problems appeared in sandwich structures are, the failures modes in the core and the faces materials, the fracture of the core material and the interaction between the fractured core and the face materials.^6,7 In sandwich structures the foam is typically the weakest part and is the first to fail under static or cyclic loading because it transfers the applied loads as shear stresses. In addition a very critical problem in sandwich structures is the debonding problem between the face and core materials.^7-9 Unstable cracking propagation and kinking in core materials represents one of the weakest failure modes in sandwich composites.^10,11 The fracture behavior in sandwich composites has been directed toward the understanding of crack propagation, and at the same time toward improving the durability of composites against fracture.^12,13 A crack flaw may be introduced during processing or subsequent service conditions. It may result from low velocity impact, from eccentricities in the structural load path, or from discontinuities in structures, which induce a significant out-of-plane stress.⁵

In our study a sandwich beam under three point bending is considered. In the core material of the beam an initially small crack oriented parallel to the longitudinal axis of the beam and very close to the upper skin interface, exists. A finite element analysis code has been developed in order to predict the position and the length of the crack when kinking of the crack occurs into the core material. The code uses the J-integral energy criterion, and the code control points of decision concerning the propagation and kinking of the crack are based on energy formulas from fracture mechanics. A general flowchart of this code is presented and numerical results are also given.

A sandwich beam is considered less than three point bending shown in Figure 1. The material properties, the loading and the crack position are presented in Tables 1-3. In the sandwich beam and into the core material an initially very small crack is considered. The position and the orientation of this initially small flaw of the body has been chosen to be 1.5mm below the upper boundary of the core material , the right crack tip lays at the midspan of the beam and the crack is oriented parallel to the longitudinal axis of the beam. This initial loading, the length of the crack as well as the material data have been obtained from the experimental verification.⁶

Figure 1 The model of the fractured sandwich beam and the applied loading.

The experimental data⁶ show that the crack propagation occurs parallel to the beam axis until the crack length reaches an approximate value between 65mm and 75mm. The direction of the crack is then suddenly changed and the crack is kinking into the core material. The sandwich beam at the same time loses completely its stiffness and is being collapsed. The presented study indents to show a numerical method which predicts the critical length of the crack as it is growing, keeping the applied to the beam load constant. The proposed procedure utilizing in the Finite Element Program ANSYS,¹⁴ a code in APDL (ANSYS Parametric Design Language), searches the maximum value of J for a particular crack length for which the direction of the crack changes. According to⁵ the crack is extended towards this direction where the maximum value of J (Jmax) occurs. From the experimental data⁶ it was shown that there is a critical crack length where kinking of the crack into the core material takes place.

In Fracture Mechanics there are two concepts studying a problem, the Stress Intensity Factor concept and the Energy concept. In this study the energy criterion and specifically the J-contour integral calculation has been used. The J-contour integral is given by:^3,4

$J={\displaystyle \underset{\Gamma }{\overset{}{\int }}\left(wdy-T_i\frac{\partial u_i}{\partial x}ds\right)}$ (1)

Where: w: strain energy density, $Ti$ :components of the traction vector,
ui: displacement vector components,
ds: length components along the contour $\Gamma .(\Gamma =\Gamma 0U\Gamma 1:\Gamma 0\to 0)$
Relation (1) is applied in a domain around the crack tip (Figure 2).

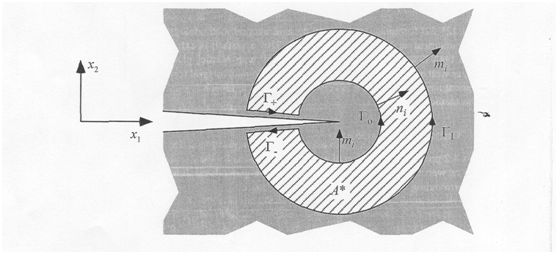
Figure 2 The domain around a crack tip where the relation (1) is applied.⁵

The energy criterion, the J integral calculation and the use of J as a critical Fracture parameter are widely used in Computational Fracture mechanics. The energy criterion or the energy approach states⁵ that the crack extension (fracture) occurs in that direction where the energy release rate (G) takes its maximum value (Gc). The Energy release rate is defined as the rate of the potential energy of the system versus $dA\left(-d\Pi /dA\right)$ , where dA is the change of the cracked area when the crack length extents incrementally. In Linear Elastic Fracture Mechanics (LEFM) as well as in a nonlinear elastic material G and J are equal under quasistatic conditions.⁵

Finite element commercial codes¹⁴ give the ability to estimate the stress intensity factors (KI, KII, and KIII) for the various modes of loading and the developed stress fields. Furthermore in order to calculate the J value given in (1) it should be defined the contour data in a path around the crack tip and the coordinate system located at the crack tip. Hence for the J-contour integral calculation it is necessary the creation of a code.

The calculation of J-contour integral in a plane linear fracture mechanics problem can be performed in two steps:

1.  Calculate the stress intensity factors (KI, KII,) and then relate them to J by the expression:⁵

$J=\frac{K_I^2}{E\text{'}}+\frac{K_{II}^2}{E\text{'}}$ , (2)

where:

$E^{\text{'}}=\{\begin{array}{c}E\begin{array}{cc}& for\begin{array}{cc}& plane\begin{array}{cc}& stress\begin{array}{cc}& condition\end{array}\end{array}\end{array}\end{array}\\ \frac{E}{1-v^2}\begin{array}{cc}& for\begin{array}{cc}& plane\begin{array}{cc}& strain\begin{array}{cc}& condition\end{array}\end{array}\end{array}\end{array}\end{array}$ , (3)

E is the Young modulus and v is the Poisson ratio.

2. Build an APDL¹⁴ code in order to retrieve store and execute tensor, matrix and algebra operations and to extract the span derivatives by a proper manipulation of the geometrical and the meshing data of the model. This was a prerequisite for the calculation of relation (1).  The procedure of defining the J integral calculation, the process and building the relevant parameters in the fractured sandwich beam confronted in this study, are presented in the next Sections.

The model shown in Figure 1 is built considering the data from Tables 1-3 and introducing them as loading, geometrical and material parameters inside an APDL code. By this way we are able to adjust the model according to the demands of the specific analysis. For example we can create various models with different materials different crack lengths, different crack positions and orientations and so on. The element type used in the proposed analysis is the two dimensional (2d) element: PLANE182.¹⁴

The proposed modeling of the sandwich beam is transformed gradually and imposes the discretion of the areas regarding the mesh density and quality in three different regions as shown in Figure 3. This discretion is a prerequisite in order to avoid the worthless consumption of computational resources and time. The model shown in Figure 3 corresponds to the maximum crack length (a=70mm).

Figure 3 The meshing strategy of the model.

The appropriate density of the elements is controlled by an equivalent division of the lines circumscribe the areas. A parameter inside the code gives the capability of defining a meaningful division of the lines at each time the crack advances, and the highly dense areas become larger.

Another very important parameter and of high priority is to define the size and the number of the elements around the crack tip. These special elements called ‘singular elements’ play an important role in fracture analyses. They are constructed by the degeneration of the 8 node quadrilateral elements which results in singular triangular elements. In elastic problems the mid-side nodes of the singular elements are moved to the $\mathrm{¼}$ points and are shown in Figure 4.

Figure 4 A common arrangement of the singular elements around the crack tip.

In order to estimate the J integral values in the post processing stage and for a good numerical approximation even though J in (1) is independent from the integration path, an adequate number of proper annular concentric paths around the crack tip must be defined. From the determined numerical values for each path an average value is finally obtained. These paths are considered as the contours $\Gamma$ of relation (1), and are shown in Figure 5.

Figure 5 The annular paths used in the J integral calculations.

The next essential point of the generalized modeling and meshing strategy arises from the observation that the loading and the stress fields are much more complicated because of the nature of the problem.

It is obvious that the crack flaw lies in the compressed area of the body, and the analysis of this kind of problem involves the approach with methodologies which take into account mixed mode fracture theories. Such an approach is the energy criterion approach namely the J-integral estimation in Fracture mechanics.

The nature of the problem (presence of a crack or material flaw in three point bending) imposes the use of contact elements between the crack flanks in order to avoid a penetration between them. The chosen elements selected in order to avoid penetration are the CONTACT178,¹⁴ point to point contact elements which are shown in Figure 6.

Figure 6 CONTACT178 point to point type contact elements, which act as an absorver between the crack flanks and prevent the penetration.

In our study in order to calculate the maximum J-integral value, it has been built in APDL format a code named ‘Jmax.lgw’. The flowchart of the proposed code is presented in Figure 7 and it includes six main steps.

Figure 7 Flowchart of the Jmax APDL code.

In the first step are defined: (1) the material and the geometrical parameters of the problem as they are presented in Tables 1-3. (2) The two types of elements which will be used (the 2-dimensional 4 node structural and 3-dimensional point to point contact elements) supplied with their proper values in their key options (i.e. the plane strain condition). (3) The initial values of the crack length and the desired meshing density. Step-1 is executed once and a repeatedly process consisting of the remaining steps is taking place. This process is controlled by the decision points 1, 2 and 3.

Step-2 undertakes the geometrical construction and the meshing of the model. It takes into account parameters as the current crack length (a) and the position of the crack. The geometry of the problem is modeled by using key points, lines and finally areas in a specified way. After the mesh process has been done, the singular elements are generated around the crack tips. Also as input, an essential parameter (e) is introduced. It works as a precondition parameter in the step by step crack advance and it takes its values after the control points 2 or 3 by taking into account the difference between the current crack length and the previous crack length as well as the directions where the maximum value of J integral occurs. It controls the amount to be added or subtracted from the crack length parameter (a) for each step.

After the mesh has be done and within step-2 a macro searches and stores the couples of the coincident nodes opposite positioned at the two crack flanks and between the crack tips. It classifies the couples regarding their position in x axis direction using the bubble sort method of array sorting.¹⁴ The operation proceeds with the insertion of the point to point contact type elements between the coincident nodes consisting each couple. The set of the coincident nodes and their spatial coordinates are stored in ascending order in an array. The macro finishes when the numbers of the circular domains of the J integral around the crack tip, and the varying in the x axis direction coordinate systems (cs) located at the left crack tip, are defined. A number of ten coordinate systems are generated. The process is repeated each time the crack length parameter (a) takes a new value. The number of the different cs can be also controlled by a parameter.

The third step shown in the flowchart (Figure 7) is executed within another macro. For reasons beyond the scope of this study we have to divide the applied load and execute the highly nonlinear solution using load steps. So, this macro defines the load data and boundary conditions and generates the load step files which will be used in the solution process. It is worth mentioning the way of applying the load, which has to be distributed over several adjacent nodes. This prevents from acting the load as an indenter. This is checked and controlled within this step also. Then the solution for the current crack length is taking place

The fourth step results the end of the solution. It involves common post processing matrix operations regarding the J integral at the different steps and stores the results data in a file. The maximum value of J integral and the direction where it occurs are stored in order to be used in the sequel. The flow control of the program and the solution data are then transferred inside the main code to the control points and to the additional operations. The direction where the maximum value of J integral occurs will then be checked at the control point-1 (Figure 7). If the direction is parallel to the x axis then the difference between the current crack length and the temporary stored value of the previous step of crack length, is checked at control point-2. If it is higher than a predefined value (m) then step-5 gives a higher value for the crack length (a) and a new iteration takes place. The amount of the crack growth is controlled by the parameter (e), and the result of this loop is that the total crack length (a) does not exceed a reasonable maximum length (amax). If it is lower than (m) the code stops and the results are stored in the output device.

If the direction where the maximum value of J integral occurs is other than the horizontal, a similar process with the previously defined, is taking place following a different path. Now the difference between the current crack length and its value at the previous step is compared again with (m) at control point -3. As to the satisfaction or not of the inequality, the program stops or begins another iteration with a reduced value of (a) which is given within step-6 and it is controlled by the parameter (e) as well. The results are stored in the output device as previously.

In the following Figure 8 the results data of J versus the different directions (acute angle with respect to the main x-axis) are presented for the first crack length (a=2mm). Figure 9 shows the iterations and the results of J for different crack lengths versus the angle between the main x axis and the direction where the maximum value of J occurs. The solution reveals that the critical crack length for a crack close to the upper skin interface is about 65mm. At this length the crack kinks into the core material, an unstable cracking propagation begins and finally the sandwich beam collapses.

Figure 8 J integral values for various angles for a crack length a=2mm.

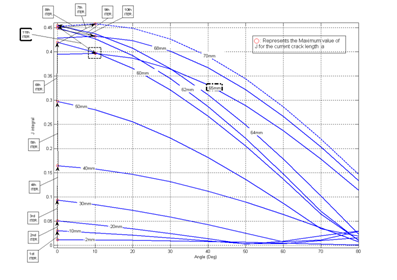
Figure 9 Solution steps and oscilation until J reaches a constant value along a direction other than 0 degrees.

Figure 10 provides a closer description of the last six iterations as the crack length exceeds the value of 60mm. For the 7th iteration a maximum value of J results at a direction different than the horizontal and at a crack length of 70mm. Next the code seeks the maximum value of J in an interval values for the crack length between 60mm and 70mm. It ‘jumps’ to a crack length of 62mm (iteration 8, now the interval is considered between 62mm and 70mm), then to 68mm (iteration 9, and the interval changes accordingly) and it continues with iterations 10 and 11. Finally the inequalities of the control points in the flowchart are fulfilled in iteration 11. Then the code exits and the final data are stored. As it can be seen from Figure 10, the maximum value of J occurs at a direction of 10 degrees as the crack length approaches the 65mm.

Figure 10 The steps of the crack propagation in order to find the non parallel to the x axis direction where the values of Jmax occur.

The results data are in good agreement with the experimental results.⁶ A further investigation based on the same procedure and with different orientations and positions of the initial small crack can be easily obtained. The two dimensional approach can be extended in the three dimensional analysis by making impertinent modifications in the code.

The proposed method of investigation, Energy criterion using the J integral approach, is much more reliable with respect to the traditional approach using the Stress Intensity Factors $(Ki,i=I,II)$ approach. Furthermore with the application of relation (2) in linear elastic problems, J and Ki are related.

J integral calculation takes into account the stress state of the body and not the crack flanks displacements inside the crack lips and near the crack tip. As the distance of the crack from the upper face increases, the influence of the shear stress field is expected to become larger.

None.

The author declares no conflict of interest.

1. Griffith AA. The phenomena in rupture and flow in solids. Philosophical transactions Series A. 1920;221:163–198.
2. Irwin GR. Analysis of stresses and strains near the end of a crack traversing a plate. Journal of Applied Mechanics. 1957;24:109–114.
3. Cherepanov GP. Crack Propagation in continuous media. Journal of Applied Mathematics and Mechanics. 1967;31(3):476–488.
4. Rice JR. A path independent integral and the approximate analysis of strain concentration by notces and cracks. Journal of Applied Mechanics. 1968;35(2):379–386.
5. Anderson TL. Fracture Mechanics, Fundamentals and Applications. USA: CRC Taylor & Francis; 2005.
6. Kulkarni N, Mahfuz H, Jeelani S, et al. Fatigue crack growth and life prediction of foam core sandwich composites under flexural loading. Composite Structures. 2003;59(4):499–505.
7. Carlsson LA. On the Design of the Cracked Sandwich Beam (CSB) Specimen. Journal of Reinforced Plastics and Composites. 1991;10(4):434–444.
8. Carlsson LA, Prasad S. Interfacial Fracture of Sandwich Beams. Engineering Fracture Mechanics. 1993;44(4):581–590.
9. Zenkert D. Damage Tolerance of Foam Core Sandwich Constructions. PhD thesis, Report 90–8, Sweden: Royal Institute of Technology; 1990.
10. He MY, Hutchinson JW. Kinking of a crack out of an interface. Journal of Applied Mechanics. 1989;56:270–278.
11. Zenkert D. Damage of Sandwich Beams with Interfacial Debondings. Composite Structures. 1991;17:331–350.
12. Berggreen C. Damage tolerance of Debonded Sandwich Structures. Denmark: PhD thesis, Department of Mechanical Engineering, Technical University of Denmark; 2004.
13. Berggreen C, Simonsen BC, Borum KK. Prediction of debond propagation in sandwich beams under FE–bared Fracture Mechanics and NDI Techniques. Journal of Composite Materials. 2007;41:493–520.
14. ANSYS Engineering Analysis System User’s Manual. USA: Swanson Analysis System Inc; 2007.