Prediction of environmental safety dynamics and management for effective functioning of the natural technical system

doi:10.15406/mseij.2021.05.00154

eISSN: 2574-9927

Material Science & Engineering International Journal

Research Article Volume 5 Issue 2

Prediction of environmental safety dynamics and management for effective functioning of the natural technical system

Bosikov Igor Ivanovich,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Klyuev Roman Vladimirovich²

¹Department of Applied Geology, North Caucasian Institute of Mining and Metallurgy (State Technological University), Russia
²Department of Industrial Power Supply, North Caucasian Institute of Mining and Metallurgy (State Technological University), Russia

Correspondence: Igor Bosikov, Department of Applied Geology, North Caucasian Institute of Mining and Metallurgy (State Technological University), 362021, North Ossetia-Alania, Vladikavkaz, Nikolayeva str. 44, Russia, Tel +7928 685 7117

Received: July 29, 2018 | Published: March 26, 2021

Citation: vanovich BI, Vladimirovich KR. Prediction of environmental safety dynamics and management for effective functioning of the natural-technical system. Material Sci & Eng. 2021;5(2):40-42. DOI: 10.15406/mseij.2021.05.00154

Download PDF

Abstract

Background: Relevance of research. The mathematical model of a singularly perturbed system with a heterogeneous morphology of the underlying surface (hilly terrain overgrown with shrubs) is considered in the article. The distribution nature of the harmful substances in this ecosystem under these infringing factors is determined. Studies using mathematical modeling and system analysis are relevant at the present stage of development and environmental safety of society.

Keywords: natural-technical system, mathematical modeling, safety, system analysis, complex estimation, diffusion equations, mining-processing complex.

Introduction

The global objectives of modeling are the issues of studying the nature of systems, the possibilities for their structural development and predicting behavior. Development and implementation of methods for predicting the dynamics and management of environmental safety of the natural-technical system is an urgent scientific task.^1-2 The expediency of the studies is unquestionable, their results enable rational planning of the economic development of the region, ensure the effective investment of public funds in environmental activities and serve as a basis for environmental monitoring.^2-3In the theory of modeling the main problems are: the development of universal approaches to the construction of models, the accuracy of the simulation of the movement of their coordinates, the estimation of error values, the adequacy of the results obtained, the identification of the systems studied, the synthesis of technical devices and hypotheses.^1–6The purpose of the research: forecasting the dynamics and management of environmental safety in mountainous areas. Objects of research: natural-technical system.

Methods

The research used generalization and system analysis of experience, theoretical research, physical and mathematical modeling, laboratory and production experiment, critical understanding of research results using methods of mathematical statistics and graphic interpretation of the results of ecological and geochemical surveys with analysis of the distribution of heavy metals over the area and identification of foci chemical pollution of soils by industrial effluents.

Results

Researches of mountainous relief, overgrown with forest have been carried out. Conventionally, this relief is displayed as follows, Figure 1. Having a set of functions, they can be used to depict a mountainous relief with a more complex structure of underlying surfaces, thereby describing the spread of harmful substances in real conditions. The form of the functions y (x) was determined by mathematical experiments using the MATCAD17 environment. Studies and experiments were conducted to determine the concentration of harmful substances in ecosystems with various underlying surfaces. Solutions of equation (1) are determined.

$u (x, y, ξ, t) = C_{1} u_{1} (x) u_{1} (ξ) + C_{2} u_{2} (2 x) u_{2} (2 ξ) ....$ $u (x, y, ξ, t) = C_{1} u_{1} (x) u_{1} (ξ) + C_{2} u_{2} (2 x) u_{2} (2 ξ) ....$ (1)

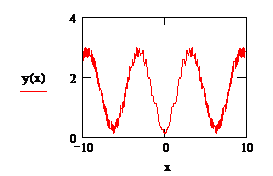
Figure 1 Display of mountain relief covered with forest.

Studies of the mountain relief, overgrown with forest, were carried out. Conditionally, this relief was displayed as follows (Figure 1). Having a set of functions $y (x) : u_{1}, u_{2}, .. u_{n}$ $y (x) : u_{1}, u_{2}, .. u_{n}$ with their help, one can depict a mountain relief with a more complex structure of underlying surfaces, thereby describing the distribution of harmful substances in real conditions. The form of the functions y(x) was determined by mathematical experiments using the MATCAD17 environment.^6–¹⁰

$y (x) = u_{1} (x) = \frac{π}{2} - \frac{4}{π} [(\cos (x) + \frac{1}{9} \cos (3 | x | x) + \frac{1}{25} \cos (10 x)]$ $y (x) = u_{1} (x) = \frac{π}{2} - \frac{4}{π} [(\cos (x) + \frac{1}{9} \cos (3 | x | x) + \frac{1}{25} \cos (10 x)]$ (2)

$y (x) : = \frac{π}{2} - \frac{4}{π} [(\cos (x + 5)) - 1 \sin (x) + \frac{1}{9} \cos (3 | x + 5 | \cdot x) + \frac{1}{25} \cos [10 (x + 5)]]$ $y (x) : = \frac{π}{2} - \frac{4}{π} [(\cos (x + 5)) - 1 \sin (x) + \frac{1}{9} \cos (3 | x + 5 | \cdot x) + \frac{1}{25} \cos [10 (x + 5)]]$ (3)

Figure 2 & Figure 3, here $y (x) : u_{1}, u_{2}, ..$ $y (x) : u_{1}, u_{2}, ..$

Figure 2 The display of a hilly relief covered with shrubs.

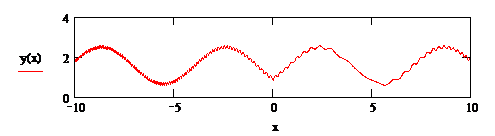
Figure 3 Display a hilly relief covered with grass.

$y (x) : = \frac{π}{2} - \frac{2}{π} [(\cos (x)) - 1 \sin (| x |) + \frac{1}{9} \cos (3 | x - 9 | \cdot x) + \frac{1}{25} \cos (10 x))]$ $y (x) : = \frac{π}{2} - \frac{2}{π} [(\cos (x)) - 1 \sin (| x |) + \frac{1}{9} \cos (3 | x - 9 | \cdot x) + \frac{1}{25} \cos (10 x))]$ (4)

In the course of the studies, the distribution of harmful substances in the hilly terrain overgrown with shrubs was determined. To do this, initially effective coefficients were found.^6–¹⁴

${\bar{u}}_{1} = \int_{0}^{10} \int_{0}^{1} y_{1} (x) y_{1} (ξ) d x d ξ = 20.741$ ${\bar{u}}_{1} = \int_{0}^{10} \int_{0}^{1} y_{1} (x) y_{1} (ξ) d x d ξ = 20.741$ , ${\bar{u}}_{2} = \int_{0}^{10} \int_{0}^{1} y_{2} (x) y_{2} (ξ) d x d ξ = 22.458$ ${\bar{u}}_{2} = \int_{0}^{10} \int_{0}^{1} y_{2} (x) y_{2} (ξ) d x d ξ = 22.458$

$y_{1} (x) = π \frac{1}{2} - \frac{4}{π} [\cos (x + 5) - \sin (x) + \frac{1}{9} \cos (3 | x + 5 |) x + \frac{1}{25} \cos 10 (x + 5)]$ $y_{1} (x) = π \frac{1}{2} - \frac{4}{π} [\cos (x + 5) - \sin (x) + \frac{1}{9} \cos (3 | x + 5 |) x + \frac{1}{25} \cos 10 (x + 5)]$ (5)

$y_{2} (2 x) = π \frac{1}{2} - \frac{4}{π} [\cos 2 (x + 5) - \sin 2 (x) + \frac{1}{9} \cos (3 | 2 x + 5 |) 2 x + \frac{1}{25} \cos 10 (2 x + 5)]$ $y_{2} (2 x) = π \frac{1}{2} - \frac{4}{π} [\cos 2 (x + 5) - \sin 2 (x) + \frac{1}{9} \cos (3 | 2 x + 5 |) 2 x + \frac{1}{25} \cos 10 (2 x + 5)]$ (6)

$γ_{1} = - 2.291$ $γ_{1} = - 2.291$ , $γ_{2} = - 2.291$ $γ_{2} = - 2.291$

The system for finding C_i(t)

${\begin{cases} μ {\dot{C}}_{1} + \frac{{\bar{γ}}_{1}}{{\bar{u}}_{1}} C_{1} - \cos t = 0 \\ μ {\dot{C}}_{2} + \frac{{\bar{γ}}_{2}}{{\bar{u}}_{2}} C_{2} - \cos 2 t = 0 \\ ..................................... \\ μ {\dot{C}}_{n} + \frac{{\bar{γ}}_{n}}{{\bar{u}}_{n}} C_{n} - \cos 2 t = 0 \end{cases}$ ${\begin{cases} μ {\dot{C}}_{1} + \frac{{\bar{γ}}_{1}}{{\bar{u}}_{1}} C_{1} - \cos t = 0 \\ μ {\dot{C}}_{2} + \frac{{\bar{γ}}_{2}}{{\bar{u}}_{2}} C_{2} - \cos 2 t = 0 \\ ..................................... \\ μ {\dot{C}}_{n} + \frac{{\bar{γ}}_{n}}{{\bar{u}}_{n}} C_{n} - \cos 2 t = 0 \end{cases}$ (7)

To determine the solution of the system (7), we used the program EULER , at $μ = 8$ $μ = 8$ (Figure 4).

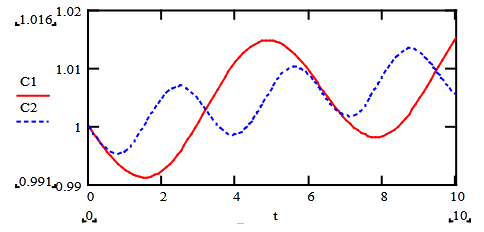
Figure 4 Charts of coefficients С1(t),С2(t).

${\begin{cases} μ {\dot{C}}_{1} - 0, 11 C_{1} - \cos t = 0 \\ μ {\dot{C}}_{2} - 0, 102 C_{2} - \cos 2 t = 0 \end{cases}$ ${\begin{cases} μ {\dot{C}}_{1} - 0, 11 C_{1} - \cos t = 0 \\ μ {\dot{C}}_{2} - 0, 102 C_{2} - \cos 2 t = 0 \end{cases}$ (8)

During the active experiment, a function was obtained that determines the nature of the change in harmful substances in the atmosphere with a hilly surface overgrown with shrubs.^10–21

$u (x, y, ξ, t) = C_{1} u_{1} (x) u_{1} (ξ) + C_{2} u_{2} (2 x) u_{2} (2 ξ) .... + C_{n} u_{n} (2 x) u_{n} (2 ξ)$ $u (x, y, ξ, t) = C_{1} u_{1} (x) u_{1} (ξ) + C_{2} u_{2} (2 x) u_{2} (2 ξ) .... + C_{n} u_{n} (2 x) u_{n} (2 ξ)$ (9)

$u_{1} (x) = π \frac{1}{2} - \frac{4}{π} [\cos (x + 5) - \sin (x) + \frac{1}{9} \cos (3 | x + 5 |) x + \frac{1}{25} \cos 10 (x + 5)]$ $u_{1} (x) = π \frac{1}{2} - \frac{4}{π} [\cos (x + 5) - \sin (x) + \frac{1}{9} \cos (3 | x + 5 |) x + \frac{1}{25} \cos 10 (x + 5)]$ (10)

$u_{2} (2 x) = π \frac{1}{2} - \frac{4}{π} [\cos (2 x + 5) - \sin (2 x) + \frac{1}{9} \cos (3 | 2 x + 5 |) x + \frac{1}{25} \cos 10 (2 x + 5)]$ $u_{2} (2 x) = π \frac{1}{2} - \frac{4}{π} [\cos (2 x + 5) - \sin (2 x) + \frac{1}{9} \cos (3 | 2 x + 5 |) x + \frac{1}{25} \cos 10 (2 x + 5)]$ (11)

Discussion

Mathematical models of the mountain terrain were developed to study the environmental safety of the environment. Analyzing the complex relief of the mountainous terrain, qualitative and quantitative characteristics of environmental indicators were determined. Using the information received, it is possible to assess in more detail and effectively the ecological situation in mountainous areas. Most of the studies were carried out without taking into account the flat terrain, therefore, it is necessary to develop a methodology for the analysis of environmental indicators for this locality, which goes beyond previous studies. Consequently, many issues need to be analyzed in the following studies on the environmental safety of different territories.¹⁸^–2¹

Research results

A methodology for managing ecosystems in the mountainous region has been developed. The possibility of increasing the efficiency of ecosystem management in a mountainous region in the conditions of a natural and technical system by using the methodology for predicting the dynamics and managing environmental safety in mountainous areas has been substantiated.

Conclusion

The use of the proposed methodology and the technical means developed by the authors using the MATCAD17 environment increases the information saturation of environmental monitoring, which contributes to the solution of issues related to the effectiveness of environmental safety management and a comprehensive assessment of the state of the environment. The impact of industrial facilities on the surrounding ecosystems of the mining complex.

Funding details

Results of the study of water and energy HPP parameters were included in the plan of research and development of the technology platform "Future of Renewable Energy Technologies" (2020), in which NCIMM (STU) has been included since 2013. The results were reflected in the Grant of the President of the Russian Federation for support of young scientists: MK-2576.2009.8 on "Investigation of water-power modes, static and dynamic stability of the high-pressure power plant".

Acknowledgments

The authors are grateful to I.E. Vasiliev for the proposal to develop a methodology for predicting the dynamics and management of environmental safety in mountainous areas, N.I. Tsygulyov for helping to compile a mathematical model of a singularly perturbed system with a heterogeneous morphology of the underlying surface.

Conflicts of interest

Authors declare that there is no conflict of interest.

References

Golik VI, Razorenov YI, Polukhin ON. Metal extraction from ore benefication codas by means of lixiviation in a disintegrator. International Journal of Applied Engineering Research. 2015;10(17):38105–38109.
Golik V, Komashchenko V, Morkun V, et al. Metal deposits combined development experience. Metallurgical and Mining Industry. 2015;7(6):591–594.
Youn RB, Klyuev RV, Bosikov II, et al. The petroleum potential estimation of the north caucasus and kazakhstan territories with the help of the structural-geodynamic prerequisites. Ustojchivoe razvitie gornyh territorij (Sustainable Development of Mountain Territories). 2017;9(2):172–178.
Bosikov II, Klyuev RV. System analysis methods for natural and industrial system of mining and metallurgical complex. Vladikavkaz. A Ju Publ; 2015:124.
Bosikov II, Klyuev RV. Development of methods and algorithms for increasing the efficiency of the functioning of the industrial and technical system. Vladikavkaz, Terek. 2018:237.
Belov PG. System analysis and modeling of hazardous processes in the technosphere. Moscow. Publishing Center "Academy"; 2003:512.
Spitsnadel VN. Theory and practice of optimal decision making. SPb: Publishing house; 2002:394.
Benardos A, Athanasiadis I, Katsoulakos N. Modern earth sheltered constructions: a paradigm of green engineering. Tunnelling and Underground Space Technology. 2014;41:46–52.
Banov M, Bech J, Ivanov P, et al. Resolving of environmental problems caused by the processing of copper ore. Bulgarian Journal of Agricultural Science. 2014;20(3):581–589.
Sokolov IV, Smirnov AA, Antipin Yu G, et al. The Effect of recovery on the effectiveness of the technology of underground mining of ore deposits. Izv. universities. Mining journal. 2012;3:4–11.
Sokolov IV, Antipin YuG. Systematization and economic-mathematical modeling of the options of opening underground reserves at the combined development of deposits. Mining magazine. 2012;1:67–71.
Andreev LI, Kravchuk IL, Han KO. Directions of system development production and maintenance of mining. GORN. 2011;11:269–275.
Trubetskoy KN, Kornilkov SV, Yakovlev BL. New approaches to obespecheniu sustainable development of mining. Mining journal. 2012;1:15–19.
Kaplunov DR, Kalmykov VN, Ryl'nikova MV. Combined Geotechnology. Moscow: Ore and Metals. 2003:560.
Zaidenvarg VE, Naviti AM, Semimobile JG. Scientific basis for integrated environmental monitoring of the area mines closed. Moscow: Rosinformugol. 2002:225.
Kabirov VR, Reyshahri EI. Economic evaluation of the effectiveness of the development group of geographically contiguous deposits of metallic minerals. Internet journal. 2014;2(21):1–8.
Balandin KA. Cost Function of the enterprise, taking into account the costs of managing a production capacity. International research journal. 2014;3-3(22):6–9.
Moore P. Assignment autonomy. International Mining. 2015:14–24.
Thrybom L, Neander J, Hansen E, et al. Future Challenges of Positioning in Underground Mines. IFAC-PapersOnLine. 2015;48(10):222–226.
Cai C, Luo X, Zhu J. Modified algorithm of combined GPS/GLONASS precise point positioning for applications in open-pit mines. Transactions of Nonferrous Metals Society of China. 2014;24(5):1547–1553.
Hammer F, Pichler M, Fenzl H, et al. An acoustic position estimation prototype system for underground mining safety. Applied Acoustics. 2015;92:61–74.