The study of optical properties of polymers is an integral part of smart materials research. It has immense potential in diverse fields spanning from structural health monitoring and underwater surveillance to medical imaging and automobile industries. Polymers are excellent candidates for these purposes due to their adaptable physical properties, one of which is their optical response to external stimuli such as temperature, pressure, magnetic fields, humidity, surrounding gases etc. Thus, being able to predict these responses is invaluable in the formulation of devices that are relevant to these applications. This paper presents a study of the simulation of the optical properties of several polymers when exposed to electromagnetic radiation, ranging from Ultra Violet to Near-Infra Red. A simulation of the influence of varying thicknesses of polymers (10, 50, 100 µm) on substrates [silicon (10, 50, 100 µm) and metal (Au) (0.025, 0.053, 0.117 µm)], on the optical properties, is presented in this study. Consequently, the results of these simulations serve as a guideline for selecting the best material configuration for the desired application. The optical bandgap of some of the polymer candidates is examined in light of Tauc’s method of analysis of the absorption coefficient variation with energy.

Keywords: Polymers, Optical Properties, Refractive Index, Modeling, Energy Gap, Absorption Coefficient, Extinction Coefficient, Dielectric Constant, Absorption Edge

There is a need to optimize the manufacturing processes in many industrial fields to improve productivity while lowering costs and increasing the overall quality of the product. The implementation of an efficient, repeatable, reproducible and profitable operational procedure is fundamental to obtaining in situ readings of process variables and performing accurate analysis of the overall state of the system.¹ Thus, it is important to study state vectors of interest. Figure 1 shows multiple parameters of interest when considering polymers for optical applications. Refractive index is one such key parameter that can give a comprehensive overview of a system. Thus, monitoring fluctuations, brought on by the variance of environmental constraints, is instrumental to predicting the materials that are appropriate for specific applications. Investigations of the optical properties of polymeric materials are currently of significant interest as these materials have many impactful applications in emerging fields such as energy, optics, optoelectronics and photonics. In the last few decades, the highly advantageous properties of these materials have enabled the development of critical technologies such as electroluminescent displays, field effect transistors, sensors and solar cells.^2-7 Low refractive index polymers are ideal for controlling light distribution in antiglare, anti-iridescence, low reflectance, and low interference products as they can eliminate disturbances from external light and increase light transmission to enhance the performance of these devices. They also have other attractive properties such as light weight, low cost and easy to process, along with low sensitivity to vibrational stress,⁸ which makes them superior to their inorganic counterparts. Low refractive index polymers have also been utilized in other electro-optical light-management applications such as anti-reflection coatings, flat light emitting technologies like OLEDs, optical adhesives, and optical waveguides.

Figure 1 Optical properties of polymers for applications in optics/optical components.

Although the thin film materials industry has historically been dominated by inorganic films, more recently, polymer films have become extremely important for a variety of applications. Consequently, they are present in various modern devices in multiple fields which include biotechnology, microelectronics, micro fluidics and optoelectronics. The need for a reduced structural requirement has enhanced the development of advanced thin film growth techniques that can be easily executed in manufacturing processes for developing devices and systems. Two-dimensional thin films hold considerable advantages over bulk materials as their large surface-to-volume ratios make them desirable candidates for applications involving surface interactions. Thin films also have greater benefits as coatings over bulk materials, since they can achieve application-specific properties that are unfeasible in the substrate material. A polymer inorganic material hybrid can be promising as a functional material.⁹

Applications of optical properties of polymers

Polymers have a variety of compelling features that make them useful for multiple areas of applications. They have the potential to help solve the storage deficiency and environmental impact caused by an increase in energy demand.¹⁰ The use of photovoltaic technologies in collecting energy from sunlight and converting it into a useful source of power is considered to be one of the most promising techniques to quell the increasing global energy demand. Amongst several available technologies, photovoltaic’s (PVs) are considered to be the cleanest way to process solar energy conversion.¹⁰ additionally; conjugated polymers are widely used in fabricating organic solar cells (OSCs). Third generation solar cells have been invented for their low costs and high- power conversion efficiencies (PCE) in various applications, for example, organic PVs (OPVs), light condensed cells, dye-sensitized solar cells (DSSCs), tandem cells, and organic–inorganic hybrid (OIH) solar cells. Although PCE of solar cells, containing organic components, seem to exhibit a shorter lifespan than those of conventional first- and second-generation solar cells, OSCs are still worth considering as they are highly flexible, light weight as well as have low manufacturing costs.⁹ Recently, the development of conjugated polymers and organic semiconductors has led to potential applications in optoelectronic devices, such as polymeric/organic light-emitting diodes (OLEDs), field-effect transistors (FETs), photovoltaic’s (PVs), nonlinear optical devices, memory storage devices, energy storage, photo detectors, and chem- and bio-sensors.¹⁰

Figure 2 depicts a summary of the multiple prospects for uses of polymers in opto-electronic and other device applications. Due to their very interesting properties, polymers are used as coatings, optical wave guides, semiconductors, sensors, and many other devices, in addition to applications in packaging. Optical fibers are used in a vast majority of everyday applications which include networking, broadcasting, and electronics. They are often used as a medium to transmit information and are usually made from pure glass or polymers because of their flexibility and small size. In recent years, polymer optical fibers have been considered to be a viable replacement for silica-based fibers. This is due to their cost effectiveness, high flexibility in bending, ease of fabrication, biocompatibility, high fracture toughness, and high sensitivity to strain. As a result, the use of these materials in optical fiber sensors has contributed to improving specific properties, making them useful for sensing purposes due to their improved response time and enhanced sensitivity. Two (Polymethylmethacrylate - PMMA and Polycarbonate - PC) of the four polymers, studied in the simulations in the present study, are excellent candidates for polymer optical fibers.⁷

Figure 2 Applications of polymers – based on their optical properties.

Optical lenses are another area of optical components in which polymeric materials are relevant. They are integral to optical materials that are designed to control light behavior i.e., diverge or converge light. Although, traditionally, optical glass has been used for this application, more recently optical polymers are replacing them. The optical behavior of lens materials is mostly studied using their transmittance, reflectance, and dispersion in specific areas. Therefore, these properties are often considered in the selection of polymers for micro-lens applications. Sultanova et al.,¹¹ were successful in incorporating PMMA and PC polymers for micro-lens applications in optical communication networks.

The refractive index is a key parameter to consider for use of polymers in optical applications. Consequently, the refractive index (RI - n) of the polymer must be tailored to suit the desired application. In order to do so, other materials should be examined to create a hybrid material. A major objective of the present study is to consider the roles of such materials (Au and Si) with polymer candidates and their influence on optical properties.⁷

Polymer based optical waveguides are integral to the development of broadband communications which include optical networking, computing systems and polymer integrated optics. These optical polymers are dependent on the phenomenon of Total Internal Reflection (TIR) which has the ability to confine light in a waveguide. Optical waveguides typically have two modes (single and multi) which depend on their frequency, refractive index, magnetic field strength and polarization.¹² Polymeric optical waveguides are excellent at refractive index modulation as a result of their thermal confinement and strong thermo-optic effect. This makes them perfect candidates for tunable filters which are vital components of optical communication systems.^12-14 these types of materials can be made of thin films integrated into optical circuits. Polymers such as poly methacrylate and polyvinyl derivatives are of interest to researchers due to their uncomplicated fabrication process and film forming including waveguide patterning.

95% of the PV modules sold today are silicon based solar cells making silicon the most popular semiconductor material.¹⁵ additionally; silicon is the second most abundant material on earth (after oxygen) as well as the semiconductor, most used, in the manufacture of computer chips. Silicon based solar cells are favorable because they have three important properties: they are low-cost, highly efficient and have a long lifespan. Conversely, Organic PV, or OPV cells, composed of carbon-rich (organic) compounds, can be tailored to improve PV cell function. However, these OPV cells are half as efficient as their crystalline silicon counterparts (or less efficient) with shorter life span.¹⁵ consequently, this makes silicon an extremely favorable substrate to consider when researching materials for use in electronic/optoelectronic devices.

This study considers the use of a metal substrate; in this simulation, gold is considered as the metal as it possesses several properties of interest to catalysis, drug delivery systems, electronics, optoelectronics and photonics. These properties include the following: gold does not corrode or tarnish; it is soft; it exhibits a combination of high electrical conductivity, optical reflectivity and a low Young’s modulus of 79 GPa. Additionally, gold has been used in biochemical sensors as signal transducers. Its inertness makes it useful in Surface Enhanced Raman Scattering (SERS) in miniaturized micro fluidic lab on chip devices.¹⁶ Gold is a particularly significant material for several applications including biosensing, chemical catalysis, electronics, optics, photonics, and plasmonics, as it possesses numerous favorable chemical, electrical, optical, and physical properties.¹⁶ In Table 1, some of the applications of low refractive index polymers are summarized.

Principles of optical properties

Previous research regarding the optical properties of polymers has primarily focused on experimental results which can be limiting since the sources for optical constants have varying information. This causes a large spread in the available data of the fundamental optical constants. Simulations are a great way to address this as they allow for a process of predicting outcomes and narrowing the search for the polymer candidates that are useful for a specific application. In this study, we consider four polymers (Polymethyl Methacrylate - PMMA, Polyethylene Terephthalate -PET, Polyvinyl Chloride - PVC and Polycarbonate - PC) for simulations of their optical properties (R, T, A), on silicon and gold substrates, in the wavelength range of visible to near-infrared region. The polymer films of thicknesses, 10µm, 50µm and 100µm, and substrates - silicon (thicknesses -10, 50, 100 µm) and gold (thicknesses - 0.025, 0.053, 0.117 µm) are considered in the simulations. The optical properties - reflectance, transmittance and absorptance are simulated utilizing predetermined n and k values for the polymers,²² silicon²³ and gold.²⁴

All the calculations of the optical properties are carried out at room temperature and under conditions of normal incidence. The wavelength dependent Reflectance (R), Transmittance (T) and Absorptance (A) are given by the following equations:

$R=\left[{\left(n-1\right)}^2+k^2\right]/\left[{\left(n+1\right)}^2+k^2\right]$   (1)

$T=\left(1-R\right)\left(e^{-\alpha t}\right)$   (2)

where, α is the absorption coefficient and is calculated from equation.

$\alpha =(4\Pi k/\lambda )$   (3)

Here, k is the extinction coefficient and λ is the wavelength of the incident photon.

$A=\left(1–R–T\right)$   (4)

The optical constants n and k (refractive index and extinction coefficient, respectively) were back calculated using the dielectric constants (ε₁ and ε₂). ε₁ and ε₂ are, respectively, the real and imaginary parts of the complex dielectric constant, ε; their relationship is as follows:

${\epsilon }_1=n^2-k^2{}^{ }$   (5)

${\epsilon }_2=2nk$   (6)

Solving the above equations, the following equations are obtained:

$4n^4-4n^2{\epsilon }_1-{\epsilon }_2{}^2=0$   (7)

$k=\left({\epsilon }_2/2n\right)$   (8)

Equations (7) and (8) lead to the determination of the values of n and k. Next, the optical properties of polymers on gold and silicon substrate were simulated. This requires the calculations of reflectance for the two layers. Reflectance for the two-layer medium is given by:

$R=\left[{\left(n_1-n_2\right)}^2+k_1{}^2\right]/[{\left(n_1+n_2\right)}^2+k_1{}^2$   (9)

where, n₁ and k₁ are the refractive index and extinction coefficient of the polymers, respectively, and n₂ is the refractive index of the substrate. The transmittance and absorptance calculations for the two-layer medium follow from equations (2) and (4), respectively.

Modelling of optical properties

Refractive index

The refractive index, dielectric constants, and dispersion properties are important parameters to observe in the modeling and development of optical properties. Consequently, these parameters have been considered in this study. Refractive index is a physical property of a material which explains the light propagation through a material. The speed of light in a material is inversely proportional to its refractive index. This means that a high refractive index causes light to pass slower within the material. The refractive index can be calculated using the expression:

n $\frac{1+\text{R}}{1-\text{R}}+\sqrt{\frac{4\text{R}}{{\left(1-\text{R}\right)}^2}-{\text{k}}^2}$ =    (10)

The extinction coefficient is a measure of how strongly a material absorbs light at a specific wavelength. It is given by the fraction of absorption per unit distance in participating medium. This can be evaluated from expression (11):

K= $\frac{\text{λα}}{4\text{π}}$    (11)

Polymer

The simulated absorptance, reflectance and transmittance spectra, under conditions of normal incidence, room temperature and varying thicknesses of polymer (PMMA), polymer/gold and polymer/silicon substrates are presented in Figures 3-9. The four polymers (i.e. without the substrate introduced), exhibit results of the optical properties that look almost identical as these polymers were selected for their similar (low refractive index) properties. Due to the similarity in the simulated optical properties, utilizing the four polymer candidates, only one set of simulations based on PMMA is discussed throughout this study.

Figure 3a presents the results of the simulated reflectance of PMMA. As expected, the simulated reflectance does not change with varying thicknesses of the polymer. Hence, a representative set of calculations, based on 10 µm thick polymer (PMMA), is presented in Figure 3. The reflectance decreases with increase in wavelength. The simulated transmittance of the polymer layer, in Figure 3b, shows multiple dips with change in wavelength. An initial increase in transmittance is followed by a slight dip at a wavelength of 1.14 microns followed by a small increase in the transmittance till 1.2 microns and then a decrease until 1.37 microns. A major dip in transmittance is observed at about 1.7 microns. The absorptance spectra in Figure 3c behaves in a complementary manner to the transmittance spectra. Amongst the materials considered in this study, PMMA thin films exhibit the lowest absorptance in the ultraviolet and visible region of the electromagnetic spectrum (Figure 3(c)).

Figure 3 Simulated (a) Reflectance, (b) Transmittance and (c) Absorptance Bare Polymer (PMMA) – 10 µm thickness.

Si substrate

In the case of bare silicon substrate, the reflectance is unaffected by a change in substrate thickness (10, 50, 100 µm). Thus a representative set of calculations based on 10 µm thick silicon is presented throughout the study. As seen in Figure 4a, the reflectance of silicon decreases rapidly from 0.4 to 1.2 µm, followed by a slow decrease from 1.2 to 2 µm. The transmittance of bulk silicon experiences an almost linear increase from 0.62 to ~1.14 µm and then it becomes constant from 1.14 - 2 µm (Figure 4c). The dip in absorptance at ~1.14 µm in silicon (Figure 4b) corresponds to its absorption edge. Absorptance in silicon increases with increasing energy (or decreasing wavelength) beyond the absorption edge (1.14 µm). It decreases from 0.62 to 0.4 µm. Silicon is a window in the infrared range of wavelengths.

Figure 4 Simulated (a) Reflectance, (b) Absorptance and (c) Transmittance Bare silicon (Si) - 10µm thickness.

Au substrate

The simulated reflectance of bare gold substrate shows a sharp peak and three dips at several wavelengths (Figure 5a). Gold, at a thickness of 0.025 microns, exhibits a peak in reflectance at a wavelength of 0.46 µm followed by three subsequent dips at wavelengths of 1.2, 1.3 and 1.99 µm. Similar behavior in reflectance of gold for thicknesses of 0.053 µm and 0.117 µm are observed. The absorptance of bare gold of thickness 0.025 µm, 0.053 µm and 0.117 µm are examined in Figure 5b. It shows a sharp dip at 0.46 µm and three sharp peaks at wavelengths of wavelengths of 1.2, 1.3 and 1.99 µm. The transmittance values are shown in Figure 5c. They are consistent with the reflectance and absorptance spectra.

Figure 5 Simulated (a) Reflectance, (b) Absorptance (c) Transmittance Bare Gold (Au) - 10µm thickness.

Polymer, Au, polymer/Au, Au/polymer

In Figure 6(a), the reflectance spectra of polymer (PMMA), Au, polymer/Au and Au/polymer are presented. As can be seen in this figure, the reflectance of polymer/Au (PMMA/Au) is very similar to that of bare gold substrate except for a very slight difference in reflectance from 0.4 to 0.7 µm. The reflectance of Au/PMMA is lesser than that of bare Au and (PMMA/Au). From these simulations, it may be inferred that the influence of PMMA, as a bottom layer, is to decrease the reflectance of Au. The sharp dips in reflectance of Au (1.2 and 1.3 µm) are observed in all the three simulations (Au, PMMA/Au and Au/PMMA)

Figure 6 (a) Simulated Reflectance of PMMA, Au, PMMA/Au; (b) Simulated Reflectance of Si, PMMA, Si/PMMA and PMMA/Si.

Polymer, Si, polymer/Si, Si/polymer

The simulated reflectance of Si, polymer, polymer/Si and Si/polymer are shown in Fig. 6b. All the results of the reflectance resemble that of silicon (also, Figure 4a). Si/PMMA exhibits less reflectance than Si and PMMA/Si. The reflectance of polymer is less than those of Si/polymer, polymer/Si and Si. The influence of thickness of bare Si and bare polymer on their transmittance is examined in Figure 7(a). As can be seen in this figure, polymer exhibits a constant high transmittance, except at 1.65-1.7 µm wavelength range. Bare Si exhibits high transmittance in the IR range of wavelengths (1.1 to 2 µm. The transmittance of 10 µm thick bare Si shows an increase in transmittance from 0.6 to 1.1 µm while thicker bare Si exhibits a similar increase in transmittance that begins at 0.8 µm. The transmittance of the polymer/Si is very similar to that of bare Si, except for a slight decrease in the peak transmittance. The order of the configuration – polymer/Si and Si/Polymer does not seem to have any influence on the simulated transmittance spectra. Hence, the simulation of transmittance of only polymer/Si is shown in Figure 7(b). The results of the simulated absorptance spectra in Figure 8(a) and 8(b) are complementary to the results of transmittance in Figure 7(a) and 7(b).

Figure 7 (a) Simulated Transmittance of PMMA, Si, at 10µm, 50µm, 100µm (b) Simulated Transmittance of Si, PMMA, PMMA/Si.

Figure 8 (a) Simulated Absorptance of PMMA, Si, at 10µm, 50µm, 100µm (b) Simulated Absorptance of Si, PMMA, PMMA/Si.

Polymer, Au, polymer/Au

The simulations of transmittance and absorptance spectra of polymer, Au and polymer/Au are presented in Figures 9 and 10. The resulting graphs in Figure 9 show that the transmittance of gold (thickness ~ 0.117 µm) is negligible. The reflectance spectra in Figure 5(a) and 6(a) complement the absorptance spectra of gold in Figure 10 (a and b). Au at a thickness of 0.117 µm, presents a peak in absorptance at a wavelength of 0.46 microns followed by an exponential decrease at ~ 0.71 µm, remains low (~ 0.05) and exhibits peaks at wavelengths of 1.2 and 1.3 µm. Also, similar behavior is observed when the thickness changes to 0.53 microns with an exponential decrease till 0.7 microns where the absorptance becomes close to zero with minute changes and a shallow peak at 1.89 microns. Regarding the two-layer simulations (Figure 10b), the transmission simulation (Figure 9) results mirror those seen with pure gold described above. This is due to the thin film polymer thickness relative to the gold substrate material properties.

Figure 9 (a) Simulated Transmittance of PMMA - 10µm, 50µm, 100µm; Au - 0.025, 0.053, 0.117 µm. (b) Simulated Transmittance of Au, PMMA, PMMA/Au.

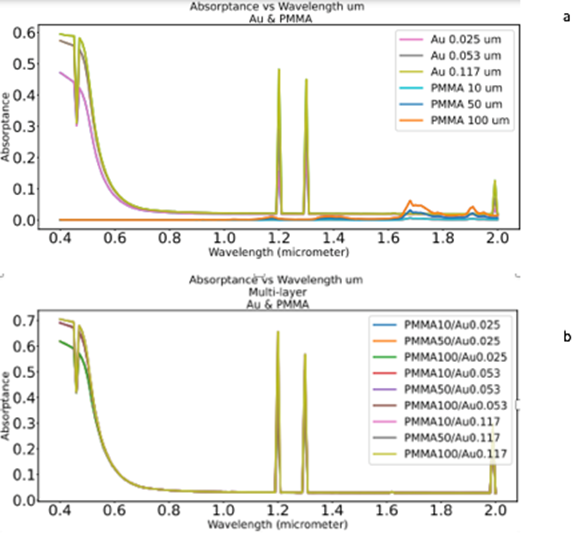
Figure 10 (a) Simulated Absorptance of PMMA, Au - 0.025, 0.053, 0.117 µm (b) Simulated Absorptance of Au, PMMA, PMMA/Au.

Polymer candidates considered in the study

Several polymers, grouped by their lower refractive indices, were considered in this study. They include PMMA (Polycarbonate (PC), Polystyrene (PS), Polyethylene Terephthalate (PET), Poly Vinyl Chloride (PVC) and Polyethylenimine (PEI). The refractive indices (n) and extinction coefficients (k) of these polymers are presented in Figures 11 and 12 respectively. In these figures, the differences in their individual optical properties (n and k) are observed. However, the simulated optical properties (R, T and A), based on their n and k, were almost identical and the difference was negligible. Consequently, only the simulated results for PMMA are presented in this study (Figures 3-10).

Figure 11 Simulated Refractive Index vs Wavelength of Low Refractive Index Polymers (PMMA PC PS PET PVC PEI).

Figure 12 Simulated Extinction coefficient vs Wavelength of Low Refractive Index Polymers (PMMA PC PS PET PVC PEI).

Optical band gap and tauc’s method

The band gap energy, for semiconductors, is the minimum energy required for an electron to transition from the valence band to the conduction band. The direct band gap value represents the energy difference between the two bands at the same value of momentum and the indirect band gap represents the difference when they have different values of momentum.²⁵ Energy gap is of significance in photonics as it demonstrates how energy from a photon can be used to produce an electron-hole pair. Optical transitions in a direct band gap occurs when the photon energy is equal to or exceeds the band gap energy as the electron receives the required energy for inter-band transition via absorption of photons. The indirect process occurs at a much slower rate because the electron needs to interact with not only the photon, but also the quanta of lattice vibration, i.e., a phonon, to undergo the required change in momentum to create an electron-hole pair.²⁶ Consequently, direct band gap materials such as GaAs, CdS, ZnS, CdSe etc. are used in light-emitting applications such as LEDs and LASERs.²⁶

The Tauc method is used to determine optical band gaps by relating the absorption coefficient to photon energy. The Tauc relation is as follows:

${\left(\alpha h\nu \right)}^{1/\Upsilon }=B\left(h\nu -E_g\right)$    (12)

where, h is the Planck’s constant, ν is the photon frequency, E_g is the band gap energy, and B is the band form parameter which depends on the transition probability and can be assumed to be constant within the optical frequency range. The nature of the electron transitions determines the ƴ factor which can be ½ or 2 for the direct and indirect transition band gaps, respectively. It can also be 3 and 3/2 for the indirect forbidden transition and direct forbidden transition, respectively. Figure 13 illustrates the different electronic transitions based on Tauc model. The resulting plot from the equation has a distinct linear region that can be extrapolated to the x-axis which gives an approximate value of the optical band gap.

Figure 13 Transition types: (a) direct allowed, (b) direct forbidden, (c) indirect allowed, and (d) indirect forbidden.²⁵

Band gap energy

The optical band gap of the polymer candidates (Table 2) is determined from the absorption spectra near the absorption edges. The plots of (α*E )² and (α*E )^1/2 versus E are presented in Figure 14 in order to approximate the direct (E_g/d/s) and indirect energy gap (E_g/id/s), respectively. The Energy band gap value was extrapolated from each graph. The values of the band gap energy of each polymer have been summarized in Table 2.

Figure 14

Simulations of the optical properties of some low refractive index polymers have been performed in the above study. These simulations are an important first step in order to identify, recommend and enhance the applications of polymers. Consequently, the optical properties (reflectance, transmittance and absorptance) of some polymer candidates [Polymethyl Methacrylate (PMMA), Polycarbonate (PC), Polystyrene(PS), and Polyethylene Terephthalate (PET)] were examined on two representative substrates – metal (Au) and silicon. The results of these simulations demonstrate that the material configurations, considered in this study, will be useful for applications in the fabrication of passive optical components, photonics and optoelectronics.

In order to increase the utility of the simulations, factors such as the effect of temperature, pressure and magnetic field must be considered. Additional candidates for substrates need to be examined along with a larger range of wavelengths and thicknesses. Model simulations such as these require a reliable database of optical constants of materials and their dependence on wavelength.

Tauc’s method of analysis was utilized to estimate the optical band gap of the four polymer candidates, PMMA, PC, PS and PET. They have been compared with the corresponding data in the literature.

None.

The authors declare that they have no conflict of interest.

None.

1. Cusano A, Cutolo A, Giordano M, et al. Optoelectronic refractive index measurements: application to smart processing. IEEE Sensors Journal. 2003;3(6):781–787.
2. Correa D, Medeiros E, Oliveira J, et al. Nanostructured conjugated polymers in chemical sensors: synthesis, properties and applications. Journal of nanoscience and nanotechnology. 2014;14(9):6509–6527.
3. Chen J, Kuo C, Lai C, et al. Manipulation on the morphology and electrical properties of aligned electrospun nanofibers of poly(3-hexylthiophene) for field-effect transistor applications. Macromolecules. 2011;44(8):2883–2892.
4. Kuo C, Lin C, Chen W. Morphology and photophysical properties of light-emitting electrospun nanofibers prepared from poly (fluorene) derivative/PMMA blends. Macromolecules. 2007;40(19):6959–6966.
5. Guillén M, Gámez F, Lopes-Costa T, et al.  A fluorescence gas sensor based on förster resonance energy transfer between polyfluorene and bromocresol green assembled in thin films. Sensors and Actuators B: Chemical. 2016;236:136–143.
6. Choi S, Persano L, Camposeo A, et al.  Electrospun nanostructures for high performance chemiresistive and optical sensors. Macromolecular Materials and Engineering. 2016;302(8).
7. Bhagyaraj S, Oluwafemi O, Krupa I. Polymers in optics. In Polymer science and innovative applications: materials, techniques, and future developments. Polymer Science and Innovative Applications. 2020;423–455.
8. Hedayati M, Elbahri M. Antireflective coatings: Conventional stacking layers and ultrathin plasmonic metasurfaces, a mini-review. Materials. 2016; 9(6):497.
9. Riede M, Spoltore D, Leo K.  Organic Solar cells-the path to commercial success. Advanced Energy Materials. 2020;11(1):583.
10. Murad A, Iraqi A, Aziz S, et al. Conducting polymers for optoelectronic devices and organic solar cells: A review. Polymers. 2020; 12(11):1–47.
11. Sultanova N, Kasarova S, Nikolov I. Characterization of optical properties of optical polymers. Optical and Quantum Electronics. 2012;45(3):221–232.
12. Ma H, Jen A, Dalton L. Polymer-based optical waveguides: materials, processing, and devices. Advanced Materials. 2002;14(19): 1339–1365.
13. Park T, Kim S, Oh M. Polymer-waveguide bragg-grating devices fabricated using phase-mask lithography. Current Optics and Photonics. 2019;3(5):401–407.
14. Chaudhuri R, Enemuo A, Song Y, et al. Polymer based resonant waveguide grating photonic filter with on-chip thermal tuning. Optics Communications. 2018;418:1–9.
15. Solar Photovoltaic Cell Basics. Office of ENERGY EFFICIENCY & RENEWABLE ENERGY.
16. Leosson K, Ingason A, Agnarsson B, et al. Ultra-thin gold films on transparent polymers. Nanophotonics. 2013;2(1):3–11.
17. Fan F, Zhang X, Li S, et al. Terahertz transmission and sensing properties of microstructured PMMA tube waveguide. Optics Express. 2015;23(21):27204-27212.
18. Dagar J, Castro-Hermosa S, Gasbarri M, et al. Efficient fully laser-patterned flexible perovskite modules and solar cells based on low-temperature solution-processed SnO2/mesoporous-TiO2 electron transport layers. Nano Research. 2018;11(5):2669–2681.
19. Wong L, Deo R, Rathnayaka  S, et al.  Leak detection in water pipes using submersible optical optic-based pressure sensor. Sensors. 2018;18(12):4192.
20. Zhang Y, Biswas R. High light outcoupling efficiency from periodically corrugated OLEDs. ACS Omega. 2021;6(13):9291–9301.
21. Davidson-Hall H, Aziz H. The role of polyethylenimine in enhancing the efficiency of quantum dot light-emitting devices. Nanoscale. 2018;10(5):2623–2631.
22. Caudill S, Tandy Grubbs W. Interferometric measurements of refractive index dispersion in polymers over the visible and near-infrared spectral range. Journal of Applied Polymer Science. 2016;100(1):65–72.
23. Palik, Edward D. Handbook of optical constants of solids II. Academic Press. 1998.
24. Yakubovsky D, Arsenin A, Stebunov YV, et al. Optical constants and structural properties of thin gold films. Optics Express. 2017;25(21):25574–25587.
25. Hussein A, Dannoun E, Aziz S, et al. Steps toward the band gap identification in polystyrene based solid polymer nanocomposites integrated with tin titanate nanoparticles. Polymers. 2020;12(10):1–21.
26. Knowles K. Direct and Indirect Band Gap Semiconductors. Dissemination of IT for the Promotion of Materials Science.
27. Yaqub N, Farooq W, AlSalhi M. Delving into the properties of polymer nanocomposites with distinctive nano-particle quantities, for the enhancement of optoelectronic devices. Heliyon. 2020;6(11).
28. Aziz S, Abdullah O, Brza M, et al. Effect of carbon nano-dots (CNDs) on structural and optical properties of PMMA polymer composite. Results in Physics. 15.
29. Aziz S, Abdullah O, Hussein A, et al. From insulating pmma polymer to conjugated double bond behavior: green chemistry as a novel approach to fabricate small band gap polymers. Polymers. 2017;9(11):626.
30. Mohammed MI, Abd El-sadek MS, Yahia IS. Optical linearity and bandgap analysis of RhB-doped PMMA/FTO polymeric composites films: A new designed optical system for laser power attenuation. Optics & Laser Technology. 2020;121.
31. Ghanem H, Saq’an S, Saadi M A, et al. On the electrical and optical properties of polycarbonate /mncl2 composite. Journal of Modern Physics. 2011;2(12):1553–1559.
32. Prasher S, Kumar M, Singh S. Gamma ray induced modifications in cellulose triacetate polymer used as a solid-state nuclear track detector. AIP Conference Proceedings, 2017;1860(1).
33. Gupta D, Kumar S, Kalsi P, et al. γ-Ray modifications of optical/chemical properties of polycarbonate polymer. World Journal of Condensed Matter Physics. 2015;5(3):129–137.
34. Mirji R, Lobo B. Linear and non-linear optical parameters of polycarbonate reinforced inorganic bismuth nitrate pentahydrate salt composite. Optical Materials. 2021;113.
35. Hussein AM, Dannoun E, Aziz S, et al. Steps toward the band gap identification in polystyrene based solid polymer nanocomposites integrated with tin titanate nanoparticles. Polymers. 2020;12(10):2320.
36. Sharma T, Aggarwal S, Sharma A, et al. Modification of optical properties of polycarbonate by gamma irradiation. radiation effects and defects in solids. 2008;163(2):161–167.
37. Tawansi A, El-Khodary A, Youssef A, Evolution of the physical properties of fecl3 filled polystyrene films. International Journal of Polymeric Materials. 2007;54(7):557–574.
38. Agam MA, Awal NN, Hassan SA, et al. Energy band gap investigation of polystyrene copper oxide nanocomposites bombarded with laser. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences. 2020;66(2):125–135.
39. Yousif E, Nabi MA, Hameed A, et al. Studying the conductivity of polystyrene using 2-(SUB.)-5-[3-(5-NITRO-FUR-2-YL)-PROPEN-2-YLDIENE]AMINO1,3,4-THIDIAZOLES as additives by measuring forbidden energy gap. Al-Nahrain Journal of science. 2020; 13(3):30–35.
40. Kumar V, Ali Y, Sonkawade R, et al.  Effect of gamma irradiation on the properties of plastic bottle sheet. Nuclear Instruments & Methods in Physics Research. Section B, Beam Interactions with Materials and Atoms. 2012;287:10–14.
41. Fawzy YHA, Abdel-Hamid HM, El-Okr MM, et al. Structural, optical and electrical properties of pet polymer films modified by low energy ar+ ion beams. Surface Review and Letters. 2017;25(03).
42. Turek M, Drozdziel A, Pyszniak KA, et al. Modification of PET Polymer Foil by Na+ Implantation. Acta Physica Polonica A. 2019; 136(2):278–284.