eISSN: 2574-9927


Research Article Volume 1 Issue 3
1GV Kurdyumov Institute for Metal Physics, Ukraine
2V Ye Lashkarev Institute for Semiconductor Physics, Ukraine
Correspondence: Gavriljuk VG, GV Kurdyumov Institute for Metal Physics, Ukraine
Received: July 27, 2017 | Published: September 20, 2017
Citation: Gavriljuk VG, Teus SM, Shanina BD, et al. On the nature of similarity in embrittlement of metals by hydrogen and surfactants. Material Sci & Eng Int J. 2017;1(3):70-79. DOI: 10.15406/mseij.2017.01.00013
A mechanism for a similar effect of hydrogen and surface–active elements, surfactants, on the structure and properties of metals is discussed based on studies of austenitic steels and using the ab initio calculations and experimental measurements of the electron structure, mechanical spectroscopy and tension tests. The similarity is originated from the local enhancement of the metallic character of interatomic bonds. The obtained results are interpreted within the frame of the electron approach to the hydrogen–enhanced localized plasticity phenomenon, HELP, in hydrogen embrittlement. The surfactants increase the density of electron states at the Fermi level and, correspondingly, the concentration of free electrons. As a response, a local decrease of the shear modulus resulted in the initiation of dislocation sources, decrease of the line tension of dislocations and distance between their assembles is expected, which facilitates the opening and propagation of cracks and mechanical degradation. The comparison with the adsorption–induced dislocation emission hypothesis, AIDE, for hydrogen and liquid metal embrittlements is carried out.
Keywords: austenitic steel, surfactants, hydrogen, electron structure, dislocations, mechanical properties
HE, hydrogen embrittlement; AIDE, adsorption–induced dislocation emission; HELP, hydrogen–enhanced localized plasticity; HEDE, hydrogen–enhanced localized plasticity; HESIV, hydrogen–enhanced strain–induced vacancies; FLAPW, full–potential–linearized–augmented plane wave; LSDA, local spin density approximation
The embrittling effect of deposited liquid metals on the mechanical properties of metallic materials has been first time declared in 1874 by Johnston1 who also emphasized similarity between this phenomenon and hydrogen embrittlement. Nevertheless, the first physical interpretation has been proposed only in 1928 by Rehbinder.2 As formulated in his short communication at the VI Congress of Russian Physicists, “the author declares the effect of the surface energy of a crystal (calcite, rock salt, gypsum, or mica) on its mechanical and other properties by decreasing the surface tension of crystal faces via the introduction of surfactants which form Gibbs–Langmuir layers at the interfaces”. This idea has been resulted in extensive practical applications for easing the cutting of tough materials due to their local embrittlement. Starting from the fifties, important practical consequences were concerned with the development of nuclear reactors using the lead-bismuth eutectic as a coolant, where the liquid-metal embrittlement, LME, creates a serious problem.3
A number of original research papers, review articles and monographies are concerned with this not ordinary phenomenon.4-9 Nevertheless, an operating mechanism remains to be debatable. The surfactants-induced decrease in the strength constitutes a topic of many studies where the Rehbinder`s concept is fundamentally bound to the Griffith`s relation between the surface free energy per unit area of the crack g , and the fracture strength with E as the Young modulus and c as the length of the initial crack formed under applied stress. The application of Griffith`s formula suggests the decrease in strength due to adsorption of surfactants on the crack surface decreasing thereby the surface energy. This rather simple thermodynamic interpretation was first time proposed in10 and still remains to be discussed.11-13
At the same time, the role of grain boundaries is noted in a number of studies devoted to a mechanism of liquid metal atoms penetration into the metal. For example, the liquid-channel grain boundary structures in ceramic materials were analyzed in,14 whereas a “self-indentation-internal-solution” mechanism has been proposed in,15 according to which the liquid metal causes grain boundary “grooving”, which removes the solid material from the bulk and dissolves it in the liquid channel. A role of the crystal structure for appearance of LME is also considered to be important. E.g., the transcrystalline LME fracture occurs in martensitic steels and binary ferrous alloys16 and it is intercrystalline in the fcc polycrystalline metals.17
Based in fact on the Rehbinder effect, the decohesion due to chemisorption on the crack surface was proposed as a mechanism for LME in.18 For substantiation of breaking the atomic bonds, this mechanism suggests a criterion of a critical relation between normal and shear stresses, which was earlier analyzed in.19 In these terms, the transcrystalline fracture can be interpreted as a result of prevailing normal stresses. At variance with this idea, LME occurs also in the amorphous iron-based materials,20,21 where both deformation and fracture proceed only through the shear processes.
Important for clarification of the operative mechanism was the observation that, including LME, embrittlement by surfactants is accompanied by a local increase of plasticity.22-24 In other words, the locally enhanced plastic deformation precedes the macrobrittle fracture. This unusual behavior was firstly interpreted as a local disintegration of solids resulted in colloidal disperse systems.4,5 Later, such approach was supported by the ideas about liquid channels14,15 and corresponding grain boundary phase transitions.25,26
However, such interpretation of preceded plastic deformation is seriously discredited by a remarkable similarity between LME and hydrogen embrittlement, HE, where local plastic flow always precedes the fracture. Systematic comparative studies of LME and HE were carried out by Lynch.27 Based on these studies, he has proposed the adsorption-induced localized-slip process to be responsible for both the LME and HE phenomena28 and, correspondingly, developed the hypothesis of adsorption-induced dislocation emission, AIDE.29 Its main idea amounts to the adsorption of hydrogen and surfactant atoms at the internal crack tips, which facilitates the nucleation and emission of dislocations. Once nucleated, the dislocations can readily move away from the crack tip under applied stress.
Along with AIDE hypothesis, hydrogen embrittlement of metals is described by hypotheses of hydrogen-enhanced decohesion, HEDE, hydrogen-enhanced localized plasticity, HELP, and hydrogen-enhanced strain-induced vacancies, HESIV. Their critical analysis is presented, e.g., in the review articles.29,30 The AIDE and HELP hypotheses seem to be the most acceptable for application to the both HE and LME processes.
Probably first time, the idea of hydrogen-enhanced mobility of dislocations as a mechanism for HE was presented by Robertson & Birnbaum31 based on the in situ observations in nickel of hydrogen-caused increase in the generation rate of dislocations, their velocity and the crack propagation rate. Later on, Birnbaum and Sofronis have developed a theory for HELP, of which the essence is the hydrogen-caused shielding of the interaction between dislocations and elastic stress centers, as calculated within the frame of continuum mechanics.32 A further development of this theory was proposed in33 and a thorough review of theoretical and experimental data can be found in.34
At the same time, the insufficiency of hydrogen elastic shielding for interpretation of hydrogen embrittlement was shown in,30,35,36 and the electron approach to HELP phenomenon has been proposed taking into account the hydrogen-caused increase in the concentration of free electrons and corresponding local decrease in the shear modulus, which changes dislocation properties. The aim of this paper is to discuss the nature of metal embrittlement by surfactants and hydrogen based on their effect on atomic interactions within the frame of HELP hypothesis in comparison with that of AIDE.
Iodine and gallium have been chosen as surfactants because of possibility to carry out the experiments at ambient temperature. Their role in mechanical degradation of metals is well known.12,37 CrNi austenitic steels doped by surfactants and hydrogen were investigated using theoretical and experimental studies of the electron structure followed by the experiments on dislocation properties and mechanical behaviour.
The effect of iodine and hydrogen on the electron structure of the fcc iron was calculated ab initio aiming to estimate a change in the interatomic bonds. The cluster (cell) of 32 iron atoms and that of 31 iron + 1 iodine or hydrogen atoms were chosen for calculations. The energy bands, the total potential, the electron density and total energy per cell have been calculated using the computational programme package Wien2k developed by the European scientific group.38 These calculations are based on the Kohn-Hohenberg-Sham density functional theory, DFT.39,40
The initial electron density for solving the Kohn-Sham equations was taken in the local spin density approximation, LSDA.41 A procedure for solving these equations is the full-potential-linearized-augmented plane wave method, FLAPW. The calculation of the exchange-correlation potential is carried out using the generalized gradient approximation in the parameters of Perdew, Burke, and Ernzernhoff,42 where the gradient terms of electron density are added to the exchange-correlation energy and its potential. The integration over the Brillouin zone is carried out using the modified tetrahedron method41 over the 15´15´15 points in k-mesh for Fe-I system and 14´14´14 points for Fe-H. The wave functions, the charge densities and the potential were expanded with L £ 10 spherical harmonics inside each ‘muffin-tin’ radius, RMT, of 2.16 a.u. and 1.10 a.u. for Fe and H atoms, respectively, and 2.16 a.u. and 2.39 a.u. for Fe and I atoms, respectively.
To obtain an equilibrium configuration of a crystal structures a full relaxation of the unit cell has been performed. By taking into account the cubic symmetry of a cell, the energy minimization procedure consists of volume relaxation and the relaxation of internal atomic positions. All calculations were performed in the full relativistic approach with the spin polarized electron states at temperature T = 0 K. Self-consistency was achieved when the root-mean square distances between the j- and (j-1) steps of the iteration procedure for the total charges and spin densities were smaller than 1.0X10-4.
Using the pure iron, nickel, chromium and manganese, four austenitic steels Cr15Ni15, Cr15Ni20, Cr25Ni20 and Cr15Ni25Mn15, see Table 1, were melted in vacuum, as ingots of 175g in the mass, followed by homogenization at 1150 °C for 24 hours. The foils of 20 mm and 0.55 mm in thickness were prepared by rolling for measurements using electron spin resonance, ESR, and X-ray diffraction, respectively. Wire specimens of 0.6 mm in diameter were obtained by cold drawing with intermediate annealing for mechanical spectroscopy. For all specimens, the final annealing was performed at 1050 °C for 30 min.
Steel |
Cr |
Ni |
Mo |
Fe |
Cr15Ni15 |
15.4 |
14.4 |
- |
balance |
Cr15Ni20 |
16 |
19.7 |
- |
balance |
Cr15Ni25Mn15 |
16.3 |
19.5 |
1.3 |
balance |
Cr25Ni20 |
25.2 |
20.2 |
- |
balance |
Table 1 Chemical compositions*.
*non-purposefully added elements were not determined.
The electron paramagnetic resonance spectrometer in the X-band of the microwave field was used for experimental studies of the electron structure. The ESR spectra were obtained at the optimum experimental conditions and recorded as derivative dP/dH from the absorbed microwave power P on the applied magnetic field H. Thereafter, all parameters were reduced to the same conditions: modulation field amplitude Hm = 0.125 G, amplifying coefficient K = 104, and microwave power P = -35 dB. A piece of the MgO: Cr3+ compound with the number of spins 1.1×1016 served as a reference sample. The analysis of the experimental spectra has been carried out based on the theory of ESR for free electrons44 and using a technique developed in our previous studies.45,46
Measurements of the amplitude-dependent internal friction for studies of dislocation properties were carried out within the strain amplitude of 0.5×10-6 to 5×10-4 using an automated inverted pendulum operating at temperatures from 80 to 580 K and frequencies of about 1 Hz. Mechanical tests were performed at room temperature using a machine Н5-К-Т of Hounsfield company, UK, with the loading rate of 1.7×10-3 s-1. Load and strain were written in the output file.
Hydrogen charging was carried out in the aerated 1N H2SO4 solution containing 100 mg/l NaAsO2 at the current density of 50mA/cm2 for 72 hours. The hydrogen/metal atomic ratio in the austenitic steels H/M = 0.2 has been estimated using the Baranowski relation47 between the volume increase and H/M for the fcc metals.
To saturate the samples with iodine, they were immersed at room temperature into a standard 5% iodine solution in the ethanol for 72 hours. Before the installation in the experimental device, EPR spectrometer, internal friction pendulum or mechanical test machine, the samples were cleaned with a soft paper. In the course of processing with gallium, the sample was kept in the gallium bath at 35, 40 or 100 °C for 5 to 68 hours. After this procedure, the samples were cleaned with a soft paper to remove the gallium drops from the sample surface.
Electron structure: calculations
The paramagnetic state of the fcc iron, g-Fe, is rather complicated for theoretical calculations because it corresponds to a disordered spin orientation and is not really non-magnetic. As mentioned in,48 the ground state of g-Fe is located at a crossing point of ferromagnetic (FM) and anti-ferromagnetic (AFM) magnetic states, which substantially depends on the atomic volume. According to neutron diffraction measurements, magnetic moments in the g-Fe form the spin density waves.49 The first-principle calculations performed using a non-collinear spin magnetism theory confirm also that the ground state of the g-Fe is a spin spiral state.50,51 At a slight increase in the lattice parameter, the fcc Fe becomes ferromagnetic. By using the collinear magnetic moments within DFT theory,51 it was shown that the spin spiral state could be well described by the double layer anti-ferromagnetic (AFMD) configuration.
The theoretical description of FM states reveals two possible magnetic configurations: low spin ferromagnetic (LS-FM) and high spin ferromagnetic (HS-FM). In consistency with the arguments mentioned in,52 we have chosen the HS-FM state to simulate the fcc g-Fe. The reasons for that are the following:
Figure 1 shows the total density of states (DOS) per cell for the spin up and spin down electron states. Iodine in the iron crystal lattice causes appearance of the bonding states at the bottom of the metallic d-band and increases the total density of states at the Fermi level (Figure 1) (Table 2).
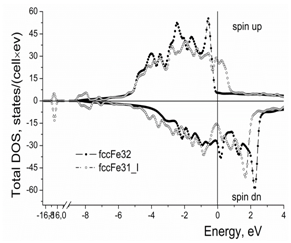
Figure 1 Effect of iodine on the total density of electron states per cell in the γ-iron crystal lattice. “Cell” means the calculated clusters of 32 Fe atoms and 31 Fe atoms + 1 I atom, respectively.
Structure |
DOS (up States), States/(cell*eV) |
DOS (dn States), States/(cell*eV) |
Total DOS |
FccFe |
5.40 |
28.71 |
34.11 |
FccFe+I |
27.24 |
16.05 |
43.29 |
FccFe+H |
5.68 |
30.52 |
36.20 |
Table 2 Calculation results on total density of states (DOS) for spin up and spin down states in the fcc iron, iron-doped iodine and iron-doped hydrogen structures.
The partial contributions to the total DOS from the electrons of outer electron shells in the iron and iodine are shown in Figure 2. The main contribution to the Fe–I atomic bonds comes from the electrons of the Fe-3d and I-5p orbitals. The hybridization between them is quite small, which indicates on a weak bonding between iodine and neighboring iron atoms in the iron lattice. However, the insertion of iodine atoms into the iron crystal lattice strikingly changes the contribution to the DOS at the Fermi level from 3d iron electrons. It constitutes 0.88 states/(eV´atom) in the pure fcc iron and 0.98 states/(eV´atom) in the Fe-I system.
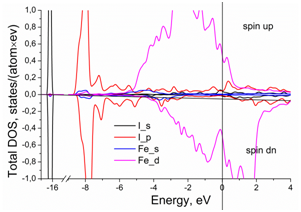
Figure 2 Partial contributions to the total density of electron states per iron atom in presence of iodine.
This result is consistent with the data of spatial distribution of electron density in its 2D projection (Figure 3). The valence states were cut off from the core and semi-core ones (according to DFT), and the plane (001) was chosen for presentation. As seen for the case of the pure fcc iron, no excessive charge accumulation occurs in the region between the iron atoms. The substitution of an iron atom for the iodine one causes the distortion of electron density at the neighboring iron atoms and increases the electron density in the interstitial area. The latter evidences the enhancement of a metallic character of interatomic bonds.
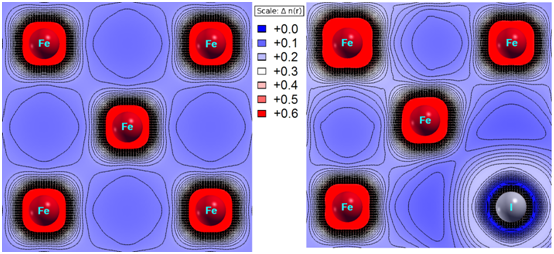
Figure 3 2d spatial distribution of valence electrons, n(r), in the calculated clusters: 32 Fe atoms, 31 Fe atoms + 1 I atom.
For comparison, the results of calculations for hydrogen in the fcc iron are presented in Figure 4. It is seen that, like iodine, hydrogen in the fcc iron increases the DOS at the Fermi level (Figure 4a) (Table 2). Hydrogen atoms in the interstitial sites are surrounded by the clouds of conduction electrons (Figures 4b & 4c), which is not the case for the iodine atoms located in the lattice sites.
Figure 4a Effect of hydrogen on the electron structure of the fcc iron: (a) total density of electron states, (b) and (c) 2d and 3d spatial distribution of valence electrons, respectively.
Electron structure: experiment
As example, the spectra of electron spin resonance of austenitic steel Cr15Ni15 measured at 77 K before and after holding in the iodine solution are presented in Figure 5a. They were recorded as derivatives from the absorbed microwave power P on the applied magnetic field H. The concentration of free electrons, as obtained from ESR measurements in steels Cr15Ni15 and Cr15Ni20, is presented in Table 3. One can see that the iodine increases the concentration of free electrons in the austenitic steels in consistency with the increase in the density of electron states at the Fermi level of the fcc iron, as presented in Figure 1. Using the same experimental technique, we have shown earlier that hydrogen also increases the concentration of free electrons in the austenitic steels.30,46
Steel |
I/Iref, 104 |
Ne, Cm-3, 1023 |
Cr15Ni15 |
|
|
Cr15Ni20 |
|
|
Table 3 Integral intensities I/Iref of ESR signals in relation to those from the reference sample and concentrations of free electrons Ne in austenitic steels before (numerator) and after (denominator) holding in the iodine solution.
Mobility of dislocations
The effect of iodine and gallium on the dislocation properties of austenitic steels in comparison with that of hydrogen was studied using mechanical spectroscopy. In absence of relaxation processes, the internal friction background is controlled by the vibrations of dislocations.56,57 Its value is the higher the larger the area crossed by the vibrating dislocations. Under condition of the constant frequency of the induced vibrations it can be used for estimation of dislocation velocity.
The increase in the concentration of free electrons, as obtained in this study using theoretical calculations and the experiment, suggests a weakening of the interatomic bonds. This should result in a decrease of the shear modulus m and, correspondingly, decrease in specific energy of dislocations, i.e. their line tension.
The strain-dependent internal friction in steels Cr15Ni25 and Cr25Ni20 doped by iodine and gallium, respectively, is presented in Figures 6a & 6b. Both surfactants increase the internal friction background at small induced strains and, starting from a definite strain, the slope , which evidences the increase in dislocation velocity in consistency with the increase in the concentration of free electrons.
Because of the high mobility of hydrogen atoms in the iron alloys, the experiment with the hydrogen-charged steels was carried out at low temperatures to prevent hydrogen degassing in the course of measurements. It is seen that hydrogen causes the same change in the studied steels (Figure 6c & 6d), which reflects similarity in the effects caused by iodine, gallium and hydrogen on dislocation properties.
Mechanical properties
Results of mechanical tests are presented in Figures 7a & 7b, Table 4. A decrease in strength and plasticity due to iodine and gallium is clearly seen. The hydrogen embrittlement of austenitic steels including those used in the present study was studied in detail in.30,35,58
Steel |
σ0.2, Mpa |
σU, Mpa |
δ, % |
|
Cr15Ni25Mn15 |
I-free |
235 ± 3 |
249 ± 15 |
37 ± 7 |
I-doped |
606 ± 13 |
573 ± 18 |
23 ± 2 |
|
Cr25Ni20 |
Ga-free |
224 ± 7 |
217 ± 12 |
49 ± 7 |
Ga-doped |
630 ± 21 |
607 ± 5 |
39 ± 2 |
|
Table 4 The yield stress σ0.2, ultimate stress σu and relative elongation δ of austenitic steels before and after doping by iodine and gallium.
Atomic interactions, mobility of dislocations and mechanical properties
The obtained results give the evidence that both, surfactants and hydrogen, affect the electron structure in a similar way, see Figures 1-4 and Table 2. The increase in the density of electron states at the Fermi level derived from the ab initio calculations is consistent with the measurements of the electron spin resonance demonstrating the increase in the concentration of free electrons, see Figure 5b, Table 3, which means the enhancement of metallic character of interatomic bonds. It is also worth noting that ESR spectra are related to the volume of the samples, i.e. the obtained result cannot be simply explained by a decrease in the surface energy.
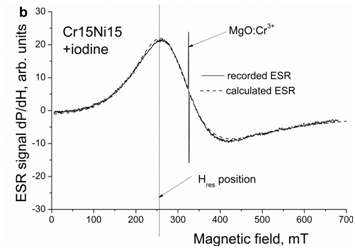
Figure 5b After holding for 72 hours in the iodine solution at RT. A narrow intensive line is the ESR signal of a piece of the reference sample MgO: Cr3+ with the number of spins 1.1×1016. Spectra are measured at 77 K.
The next remarkable effect of iodine and gallium is the increase in the velocity of dislocations, Figures 6a & 6b. A similar behavior is observed in hydrogen-containing austenitic steels (Figures 6c & 6d), which in both cases corresponds to the enhancement of dislocation slip. This enhancement is caused by hydrogen clouds which follow moving dislocations and locally increase the concentration of free electrons in their vicinity.
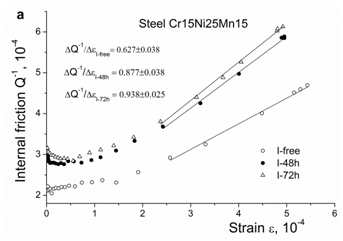
Figure 6a Strain-dependent internal friction in austenitic steels before and after contact with surfactants: iodine, steel Cr15Ni25Mn15.
At the same time, it is hardly possible that dislocation slip can be accompanied by migration of surfactant atoms. Rather, because of non-homogenous distribution of surfactant atoms, the facilitation of slip is expected in some limited areas, where the surfactant atoms are present. The embrittling effect is illustrated in Figure 7, Table 4 for iodine and gallium in austenitic steels. Such embrittlement is also observed in a number of hydrogen-charged austenitic steels including those used in this study.34,35,58 A limited penetration of surfactant atoms and their non-homogenous distribution in the solid solution is supposed to be a reason for localization of the enhanced plastic deformation followed by the macrobrittle fracture.
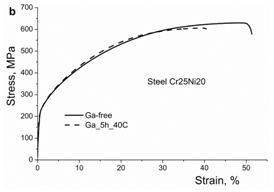
Figure 7b Effect of iodine on the stress-strain curves of austenitic steels Cr15Ni25Mn15 and Cr25Ni20, respectively.
Comparative analysis of AIDE and HELP hypotheses.
As mentioned in Introduction, the essence of AIDE hypothesis in relation to both HE and LME is that hydrogen and surfactants facilitate the nucleation of dislocations at the internal surface of crack tips and their emission. Three statements are remarkable in this hypothesis, particularly in relation to HE:
It is also claimed29 that “nucleation and growth of voids at second-phase particles, slip band intersections or other sites in the plastic zone ahead of cracks occur because stresses required for dislocation emission are sufficiently high …”. The AIDE mechanism is supposed to be predominant in both HE and LME phenomena.28,29
First, some criticism can be expressed in relation to applicability of the AIDE hypothesis for hydrogen embrittlement. This hypothesis ignores the role of hydrogen in the nucleation of cracks under applied stress and, thereby, suggests the occurrence of preexisting cracks or their formation under stress whatever hydrogen is present or not. The microcracks are really formed in the course of cathodic hydrogen charging because of a sharp concentration profile within the surface layer. However, it is not the case for gaseous hydrogenation. It is worth noting in this relation that one of the earliest proposed mechanisms of HE was concerned with the so-called pressure-expansion theory,59 which included precipitation of gaseous hydrogen in the microvoids, their growth under increased internal hydrogen pressure and consequent plastic deformation leading to microcracks or void coalescence. Critical for estimation of that mechanism were the experimental data,60 according to which the gaseous hydrogenation at 1 bar pressure without crack formation was found to cause a greater embrittlement of high strength steels in comparison with electrolytic charging accompanied by crack nucleation.
Second, the hydrogen-caused formation of the voids is not properly substantiated in the AIDE hypothesis. In fact, it does not need any presence of the above mentioned second-phase particles or high stresses for dislocation emission. Like any other interstitial elements in the metal solid solution, hydrogen increases the thermodynamically equilibrium concentration of vacancies, which was theoretically predicted in,61,62 and first confirmed in the experiments on the hydrides63 and austenitic steels.64 Be created by hydrogen within their clouds at dislocations, vacancies cannot follow them in the course of plastic flow and are expected to form the nanovoids along the slip planes.
In contrast, the HELP hypothesis is based on the primary role of interaction between hydrogen atoms and dislocations. Due to this interaction, the hydrogen clouds around dislocations create a shield for their stress fields, according to,32 or, due to the hydrogen-increased concentration of free electrons, locally decrease the shear modulus, according to.30 This local change in the atomic interactions leads to the following consequences: (i) a decrease of the stress for emission of dislocations , where b is the Burgers vector and L is a distance between pinning points; (ii) the enhancement of dislocation mobility due to decrease in the specific energy of dislocations, i.e. their line tension , where ℜ is the radius of the dislocation curvature; (iii) a decrease in the distance between dislocations in the pile-ups, , which assists the nucleation of cracks due to the increase in the number of dislocations n, and, correspondingly, the stress at the leading dislocation , where t is the active shear stress in the slip plane. This decrease in the distance between dislocations is experimentally confirmed in65 and should facilitate the opening of microcracks.
Two main objections were raised by Lynch against applicability of HELP hypothesis for hydrogen embrittlement. According to the first one,28 the velocity of cracks propagation can be too high in comparison with diffusion of hydrogen atoms ahead of the cracks, and even hydrogen transfer by dislocations is claimed to be not sufficient to provide a required hydrogen migration rate. In the second one,66 it is argued that, even at rather high hydrogen content, hydrogen embrittlement is absent in austenitic steels at temperatures above 70 °C and in a -titanium alloy at ambient temperatures, whereas “hydrogen-increased dislocation activity” still occurs.
This criticism can be easily replied based on the following experimental data. First, the hydrogen brittleness disappears at some critical strain rates,67,68 which clearly indicates on the hydrogen transfer by dislocations as a prerequisite for HE. If hydrogen clouds leave the dislocations, embrittlement disappears.
Second, as shown in,69 the enthalpies of hydrogen atoms migration, Hm, and their binding to dislocations, Hb, control the temperature for condensation of hydrogen atoms at dislocations, Tc, and, correspondingly, the temperature range of hydrogen brittleness. Above Tc, the interaction between dislocations and hydrogen atoms is weakening and, whether brittleness is being realized or not, depends on how steep the dispersal of hydrogen clouds proceeds. However, diluted hydrogen clouds at dislocations are still retained and the above mentioned “hydrogen increased dislocation activity” is observed up to high temperatures.
In relation to the different temperature region of hydrogen embrittlement in austenitic steels and titanium alloys, the point is that both, Hm and Hb, are significantly smaller in the titanium alloys.69 This is why, in contrast to austenitic steels, even at rather high hydrogen contents, the brittleness in the titanium alloys occurs below ambient temperatures. Just for this reason, hydrogen is used as temporary alloying element for processing of titanium alloys .70,71
Therefore, the HELP hypothesis more adequately describes hydrogen embrittlement in comparison with the AIDE one. So far, a mechanism similar to HELP was not applied for interpretation of LME or, more generally, for surfactants effect on mechanical behavior of metals. The theoretical and experimental data obtained in this study show that surfactants and hydrogen in austenitic steels change the atomic interactions and behavior of dislocations in the same way, which allows to suppose a physical nature for deterioration of mechanical properties similar to that in the HELP phenomenon.
None.
The author declares no conflict of interest.

©2017 Gavriljuk, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.