Magnetic drug targeting can be used for locoregional cancer therapy, although the limitation is minuteness of the induced force. A new and simple procedure to enhance the magnetic force is changing the shape of carrier particles. It has been mathematically proved that exerting much stronger magnetic dipoles to nanowires are more possible than to spheres with the same volume. The magnetic dipole of wires having aspect quotient (ratio of length to diameter) of 3 is higher than the spheres of the same volume. Nanowires with α=5 have magnetic dipoles 1.95 times greater than the spheres with the same volume. At a fixed radius, the magnetic dipole increases with the volume of the drug carrier. Magnetic targeting depth is an important parameter depending on the aspect quotient α of particles. Calculations show that the depth of targeting can exceed 8.5cm if a nanowire with 15nm radius and length larger than 150 nm is used as the drug carrier. This depth is 1.7 times more than that reported by previous authors for spherical particles with the same-volume.

Keywords: drug delivery, magnetic targeting, magnetic force, magnetic nanowire, magnetic targeting depth

These days, an important desire of researchers is to deliver medicine to the exact disease tissues. For instance, chemotherapy is a contemporary therapy in which less than 0.1% of the medicine is absorbed by the tumor cells; while the remaining (99.9%) affects healthy cells.^1,2 Magnetic drug targeting (MDT) is of the newest innovated methods to help treatment of a localized disease such as cancerous tumors. Ideal MDT treatment is based on binding the drug to the magnetic particle or such a similar method for linking drug to the magnetic nanoparticles, and then magnetic particles are injected into the bloodstream at an appropriate location. Careers go towards the disease tissues. Externally-applied magnetic forces push the careers to extract from streams and enter to the tumor tissues. These careers are activated by pH, temperature, enzyme or a magnetic trigger³ which requires to control the motion of magnetic particles in the body by magnetic actuators (Figure 1).^2,4,5 After injection of therapeutic magnetic particles into the patient’s bloodstream, external magnets will conduct the particles towards the tumor locations,^6–12 blood clot,¹³ or infection.^14,15 Magnetic-fields are much more convenient than light, electric-field and ultrasound^16–18 to control the motion of the therapeutics inside the body on the grounds of their depth of penetration for deep tumors therapy. Also, magnetic fields can be applied with the strength of 8T for adults and 4T for children in DC type without any problem.^19–22 Todays, MDT in cancer therapy is limited to superficial tumors.^7,23 If the depth of targeting increases, this method could be applied to a wide range of diseases. Delivering a magnetic drug to in-vivo locations being far from the magnets or magnetic-field source^9,11,24–31 depends on the applied magnetic field strength and its gradient which decreases quickly with getting away from magnets^32,33 The strength of the magnetic field in MDT is between 70 Mt³⁴ and 2.2 T³⁵ with gradients of 3 T/m³⁶ to 100 T/m.³⁷ A targeting depth of 5cm has been examined in the human body using magnetic particles of 100nm size as the carriers and magnetic field of 0.2–0.8 T.^32,38 Moreover, targeting depth has increased to 12cm in animal experiments with larger carriers (500nm–5 mm) and 0.5 T magnetic field.³³ One of the important parameter in targeting depth is particle size. When MDT is used, it should be considered that the particles must be smaller than 600nm to have the ability to be extracted from blood vessels towards tumor tissues^22,39–46 and even be smaller than the mentioned size to become hidden from phagocyte system because large particles are removed by this system very fast. Researches show that particles with 100 nm size would be in blood stream for about 30 min and hence it should be extracted from blood vessels before this time.^47,48 Another thing that should be considered is the magnetic force that should be small on small particles since it increases with particles volume increase in a direct relation.⁴⁹ According to this statement, if particle size decreases ten times, the magnetic force will decrease one thousand times. Hence, with a high magnetic field (e.g. 41T) and high magnetic fields gradient (e.g. 0.5 T/cm) the force would be in the range of piconewtons.^49–51 Therefore, it is needed to know which location is able to reached by MDT.⁹ Maximum depth of targeting being attained in the human body is 5cm^32,48 and hence, increasing depth of magnetic targeting is still a challenging desire for tumor therapies.^52–54 This is why we chose our goal of this study basically upon the increasing of applicable magnetic forces plus the magnetic drug catching depths. To achieve this goal, we established a computational model for magnetic dipoles of nanowires and nano spheres and compared the obtained forces of magnetic particles for drug delivery. We showed that magnetic nanowires can induce magnetic forces as well as magnetic targeting depths much higher than that of spherical particles. The former, thus, can provide much better controllability for localized cancer therapy.

Figure 1 Schematic view of magnets for directing MNPs in the human body.⁶

To compute the magnetic dipole of a spherical nanoparticle we use the following equation:^55,56

 $\overrightarrow{m_p}=\frac{4\pi a^3}{3}\frac{\chi }{1+\raisebox{1ex}{$\chi $}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\frac{\overrightarrow{B_0}}{{\mu }_0}$    (1A)

Where, , χ and  are magnetic dipole nanoparticle, the radius of them, magnetic susceptibility, and the amplitude of the external magnetic-field, respectively. The magnetic force of the spherical particle of Eq.1-a is:⁵⁶

 $\stackrel{\rightharpoonup }{F_m}=\left(\stackrel{\rightharpoonup }{m_p}.\stackrel{\rightharpoonup }{\nabla }\right).\stackrel{\rightharpoonup }{B_0}$    (1b)

In Eq.1-b,  is the magnetic force on the particle with magnetic dipole of from external magnetic-field. In order to calculate the magnetic dipole of a nanowire numerically, we firstly defined a cylinder and generated a mesh on it to describe the model parameters. For this purpose, we divided the cylinder into discs and then divided every disc to a number of rings. Figure 2 shows the schematic picture of the mesh for a nanowire in cylindrical coordinates. In this model, we consider a single super paramagnetic nanowire in a constant external magnetic-field and then calculate the magnetization and the magnetic dipole of the wire. The correlation between magnetization and magnetic current is as follows:

Figure 2 Meshes schematically generated on wire.

$\nabla \times M^{ ⃑}=\left(J\_m \right){ }^{⃑}$    (2)

Where is the vector of magnetization, and  is the magnetic current density. The boundary condition for Eq.2 is expressed as follows:

$\left(J\_ms \right){ }^{⃑}=M^{⃑} \times {\left(a\_n \right)}^{⃑}$    (3)

In which,  is the surface magnetic current density and  is the vertical vector at wire surface.

For magnetic field intensity  without free current, we have:

$\nabla \times \stackrel{\rightharpoonup }{H}=0$    (4)

The relationship between magnetization and magnetic-field and linear magnetization with respect to is defined as:

$\frac{1}{{\mu }_0}\stackrel{\rightharpoonup }{B}=\stackrel{\rightharpoonup }{M}+\stackrel{\rightharpoonup }{H}$    (5)

The combination of (5) and (6) yields to:

 $\frac{1}{{\mu }_0}\stackrel{\rightharpoonup }{B}=\stackrel{\rightharpoonup }{M}+\frac{1}{\chi }M=M\left(1+\frac{1}{\chi }\right)$    (7)

Eq.4 and 6 yield to:

$\nabla \times \stackrel{\rightharpoonup }{M}=0$    (8)

Now, we should calculate magnetic-field in every point of the wire. For this purpose, we have used superposition principal of vectors, like:

$B=B_0+B_{other elements}$    (9)

B_{other elements} is the sum of all magnetic-fields that are generated with magnetized nanowire elements. Eq.10 shows B_{other elements} components in the wire with considering Eq.2, 3 and 8:

 $\stackrel{\rightharpoonup }{B}\left(r,z\right)={\stackrel{\rightharpoonup }{B}}_0+{\displaystyle \sum }_{i=1}^p{\stackrel{\rightharpoonup }{B}}_i$    (10)

B_i is the magnetic field of superficial current for j^th ring on the surface and p is the number of superficial rings. In order to compute the magnetic field originated from the surface current on the external surface of wires, the rings shown in Figure 3 are considered. In this figure, r_i and z_i are radius and height of the ring on the external surface of the wire with superficial current density and r and z are the coordination of the point of interest to compute its magnetic field. In wire, we have three kinds of external surfaces: down, top and side. The surface current for all three surfaces are calculated as follows:

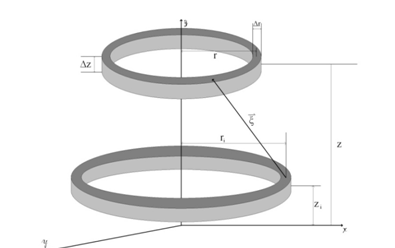
Figure 3 Schematic representation of the wires and their respective coordinates.

 $I_{i-down}=M_r\left(r_i,0\right).\Delta r.\hat{\phi }$    (11)

 $I_{i-top}=-M_r\left(r_i,L\right).\Delta r.\hat{\phi }$    (12)

 $I_{i-sidelong}=M_z\left(R,z_i\right).\Delta z.\hat{\phi }$    (13)

According to Biot– Savart law, the magnetic field of i^th surface ring (B_i) in point (r, z) is expressed as follows:

 $B_i\left(r,z\right)=\frac{{\mu }_0}{4\pi }{I}_i.{{\displaystyle \oint }}^{\text{}}\frac{\stackrel{\rightharpoonup }{dl}\times \stackrel{\rightharpoonup }{\xi }}{{\left|\stackrel{\rightharpoonup }{\xi }\right|}^3}$    (14)

In which, is the distance vector from every point on the ring to point(r, z) and the integral is on the environment of the ring with center (0, z_i). For simplification, we write the following equation:

 $\stackrel{\rightharpoonup }{f}\left(r_i,z_i,r,z\right)=\frac{1}{4\pi }{{\displaystyle \oint }}^{\text{}}\frac{\stackrel{\rightharpoonup }{dl}\times \stackrel{\rightharpoonup }{\xi }}{{\left|\stackrel{\rightharpoonup }{\xi }\right|}^3}$    (15)

Then we can rewrite the Eq.14 according to the Eq.15:

 $B_i\left(r,z\right)={\mu }_0{I}_i.\stackrel{\rightharpoonup }{f}\left(r_i,z_i,r,z\right)$    (16)

From Eqs.10, 11, 12, 13 and 16, we have:

${\stackrel{\rightharpoonup }{B}}_k\left(r_k,z_k\right)=\stackrel{\rightharpoonup }{B_0}+{\mu }_0\left({\displaystyle \sum }_{i=1}^q{M}_z\left(R,z_i\right).\Delta z.\stackrel{\rightharpoonup }{f_z}\left(R,z_i,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p{M}_r\left(r_i,0\right).\Delta r.\stackrel{\rightharpoonup }{f_{}}\left(r_j,z_j,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p-M_r\left(r_i,L\right).\Delta r.\stackrel{\rightharpoonup }{f}\left(r_j,z_j,r_k,z_k\right)\right)$    (17)

Where k is the number of the rings and  is the magnetic field in k^th ring.

If we write the Eq.17 on radial and vertical directions, we will have:

${\stackrel{\rightharpoonup }{B}}_{kz}\left(r_k,z_k\right)=\stackrel{\rightharpoonup }{B_0}+{\mu }_0\left({\displaystyle \sum }_{i=1}^q{M}_z\left(R,z_i\right).\Delta z.\stackrel{\rightharpoonup }{f_z}\left(R,z_i,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p{M}_r\left(r_i,0\right).\Delta r.\stackrel{\rightharpoonup }{f_z}\left(r_j,z_j,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p-M_r\left(r_i,L\right).\Delta r.\stackrel{\rightharpoonup }{f_z}\left(r_j,z_j,r_k,z_k\right)\right)$    (18)

${\stackrel{\rightharpoonup }{B}}_{kr}\left(r_k,z_k\right)={\mu }_0\left({\displaystyle \sum }_{i=1}^q{M}_z\left(R,z_i\right).\Delta z.\stackrel{\rightharpoonup }{f_r}\left(R,z_i,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p{M}_r\left(r_i,0\right).\Delta r.\stackrel{\rightharpoonup }{f_r}\left(r_j,z_j,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p-M_r\left(r_i,L\right).\Delta r.\stackrel{\rightharpoonup }{f_r}\left(r_j,z_j,r_k,z_k\right)\right)$    (19)

Where andare vertical and radial components of the magnetic field in each ring, and and  are vertical and radial components of Eq.15. If we apply Eq.7 into Eqs.18 and 19, the final equations can be obtained:

${\displaystyle \sum }_{i=1}^q{M}_z\left(R,z_i\right).\Delta z.f_z\left(R,z_i,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p{M}_r\left(r_i,0\right).\Delta r.f_z\left(r_j,z_j,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p-M_r\left(r_i,L\right).\Delta r.f_z\left(r_j,z_j,r_k,z_k\right)-M_z{}_k\left(1+\frac{1}{\chi }\right)=\frac{-1}{{\mu }_0}{B}_0$    (20)

${\displaystyle \sum }_{i=1}^q{M}_z\left(R,z_i\right).\Delta z.f_r\left(R,z_i,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p{M}_r\left(r_i,0\right).\Delta r.f_r\left(r_j,z_j,r_k,z_k\right)+{\displaystyle \sum }_{i=1}^p-M_r\left(r_i,L\right).\Delta r.f_r\left(r_j,z_j,r_k,z_k\right)-M_r{}_k\left(1+\frac{1}{\chi }\right)=0$    (21)

Now, we have two series of variables:  and. If we write Equations 20 and 21 in every n rings of the wire, we will get 2n equations as n rings become magnetic on both vertical and radial directions and a specification matrix with size 2n×2n for magnetization of the wire. Equation 22 shows the relationship between the variables:

 $W_{M 2n\times 2n}\times {\left(\begin{array}{c}{M}_z\\ M_r\end{array}\right)}_{2n\times 1}=\frac{-1}{{\mu }_0}{\left(\begin{array}{c}{B}_{0 }\\ 0\end{array}\right)}_{2n\times 1}$    (22)

If we suppose B₀1 and solve the equations, we can obtain magnetization matrix for every B₀ such as follow:

 $M_{B_0}=M_{B0=1}\times \left|\stackrel{\rightharpoonup }{B_0}\right|$    (23)

Where is magnetization matrix for external magnetic field and  is magnetization matrix for B₀=1. The magnetic field of the cylindrical magnet is expressed as follows:⁵⁶

 $B_{magnet}\propto \frac{1}{d^2}$    (24)

Where and d are magnetic field and diameter of the cylindrical magnet, respectively.

The magnetic field gradient of a cylindrical magnet is expressed as:

 $\frac{\partial B_{magnet}}{\partial d}\propto \frac{1}{d^3}$    (25)

With attention to the Eq.1-b, 24 and 25, the magnetic force is related to d as follow:

 $F_m\propto \frac{1}{d^5}$    (26)

Considering the Eq.26, we can compare the depth of magnetic targeting according to:

 $\frac{d_w}{d_s}=\sqrt[5]{\frac{m_w}{m_s}}$    (27)

Where d_w and d_s are the depth of magnetic targeting for wires and spherical particles, respectively. The parameters m_w and m_s are magnetic dipoles of nanowires and spherical particles.

To compare the magnetization and the magnetic dipole of the spherical and the cylindrical nanoparticles, we use the corresponding parameters in a uniform unit magnetic field. Table 1 shows different specifications used for simulation in this research. With the parameters shown in this table, 175 combinations exist. We chose these combinations to show the effect of geometry on magnetic force and the depth of magnetic targeting. Changing the aspect ratio (α) at a constant volume results in the variation of radius and the height of the wire. For every sphere with radius of r, the volume is calculated and then for every α, the radius and height of the corresponding wire are calculated and then the magnetization and the magnetic dipole of the wire is simulated at different susceptibilities. (Figure 4) (Figure 5) show the magnetization in vertical and radial directions with radius r30 nm and α5. Figure 5 shows the magnetic dipoles of wires in the vertical direction for different sizes with various aspect ratios and different susceptibilities. Radius and height of the wire are calculated from the following equations as a function of α:

Figure 4 Magnetization of a wire with r=30 nm, α=5 and susceptibility=500: (A) magnetization in the vertical direction and (B) magnetization in the radial direction.

Figure 5 Vertical magnetic dipole of the nanowire versus the ratio α at different susceptibilities for rs equal to: (A 15nm, (B) 30nm and (C) 50nm.

$V=\frac{4}{3}\pi r_s{}^3$    (28)

$R=\frac{1}{2}\sqrt[3]{\frac{4V}{\pi \alpha }}$    (29)

$V=\frac{4}{3}\pi r_s{}^3$    (30)

V is the volume of the spherical particle with radius r_s. R and L are the radius and length of the corresponding nanowire. In Eqs.28, 29 and 30, it is assumed that the volume of the wire and the spherical particle are the same. Then, for all aspect ratios, radius and height of the wires were calculated. As shown in Figure 5, it is clear that increasing the susceptibility from 500 to 2000 has no influence on the vertical magnetization, being also the same for spherical magnetization. Instead of materials with high susceptibility, we, therefore, chose materials with high saturation limit. This will result in more magnetization without saturation. Figure 6 shows that vertical magnetic dipole of the nanowires with respect to their volume is linear. Likewise, the magnetic dipole of spherical particles is linear. The slope of graphs increases as the aspect ratio increases. At α=3, the behavior of wires and spheres is the same. More increase in the aspect ratio up to 5 retains the double magnetic dipole at a constant volume. It is clear that magnetic dipole increases with α, directly; however, if α is more than 5 or 6, the mechanical solidity of wires will decrease. In this research, we can increase the magnetic dipole of the particles merely by changing their geometry. Comparing the magnetic dipole of a wire having α=5 and radius =15 nm with a spherical particle of radius =15nm, we found out that the magnetic dipole of the former is 15 times larger than that of the latter. This means that if we use a wire with specifications above, the magnetic force will be 15 times greater than the corresponding spherical particle. When using nanowires, we can increase the volume without increasing their radius and simultaneously increase the magnetic dipole merely with α enhancement. These two specifications can be used to increase the depth of target and diffusion rate of the drug carrier particles toward the tumors without increasing the radius of particles. Figure 7 shows the magnetic dipole of nanowires and spherical particles as a function of susceptibility at different α ratios for radii 15, 30 and 50nm. As was shown in the mentioned figures, the relationships for wires of α=3 are similar to the spherical particles while increasing the susceptibility of the magnetic materials above 500 has no independent influence on the magnetic dipole.

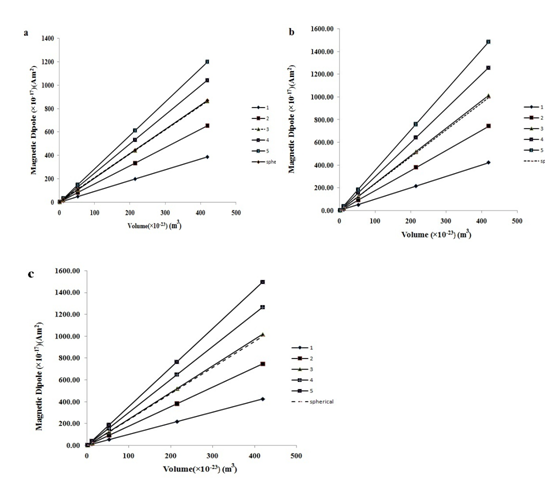
Figure 6 Magnetic dipole versus volume of nanowires and spherical particles for different aspect ratios at susceptibility equal to: (A) 20, (B) 500 and (V) 2000.

Figure 7 The magnetic dipole of wire and spherical particles versus susceptibility at various aspect ratios and rs equal to: (A) 15nm, (B) 30nm and (C) 50nm.

For in-depth magnetic drug targeting, the most important parameter is the force which can be increased by magnetic dipole of the particles. For increasing the magnetic dipole of the particles, there two ways including (i) increasing volume of the particles and (ii) increasing the ratio of length to diameter of the particles. With spherical particles, the former way reduces the mobility of the particles. The volume of the particles has thus to increase without enhancement of their radius. This way is obviously not feasible. By employment of cylindrical particles having high aspect ratios, this action is, however, possible. The magnetic dipole of the wires having an aspect ratio of 3 is equal to the spherical particles of the same volume. With aspect ratios larger than 3, the magnetic dipoles of wires are larger than the spherical particles of the same volume. Choosing an intersection radius of 15 nm and an aspect ratio of 5, we can attain magnetic dipole of 14.6 times larger than that of the spherical particle of the same radius. If we apply these parameters to the Eq.27, we will attain 70% deeper magnetic targeting than the spherical particles. This means that the geometry change has an increasing effect on the applied force as particle volume expansion does occur.

Deputy of research of the Sharif University of Technology is thanked for continued support of Seed of Design and Accomplishment of New Processes for Production and Application of Advanced Materials.

Author declares that there is no conflicts of interest.

1. Reszka R, Beck P, Fichtner I, et al. Body distribution of free, liposomal and nanoparticle-associated mitoxantrone in B16-melanoma-bearing mice. Journal of Pharmacology and Experimental Therapeutics. 1997;280(1):232–237.
2. Mirab F, Eslamian M, Bagheri R. Fabrication and characterization of a starch-based nanocomposite scaffold with highly porous and gradient structure for bone tissue engineering. Biomedical Physics & Engineering Express. 2018;4(5):055021.
3. Cherry E, Eaton J. Simulation of magnetic particles in the bloodstream for magnetic drug targeting applications. 2012.
4. Nacev A, Komaee A, Sarwar A, et al. Towards control of magnetic fluids in patients: directing therapeutic nanoparticles to disease locations. IEEE Control Systems. 2012;32(3):32–74.
5. Ebrahimian Pirbazari A, Fakhari Kisom B, Ghamangiz Khararoodi M. Anionic surfactant-modified rice straw for removal of methylene blue from aqueous solution. Desalination and Water Treatment. 2016;57(39):18202–18216.
6. Shapiro B. Towards dynamic control of magnetic fields to focus magnetic carriers to targets deep inside the body. Journal of magnetism and magnetic materials. 2009;321(10):1594–1599.
7. Lübbe AS, Bergemann C, Riess H, et al. Clinical experiences with magnetic drug targeting: a phase I study with 4′-epidoxorubicin in 14 patients with advanced solid tumors. Cancer research. 1996;56(20):4686–4693.
8. Johannsen M, Gneveckow U, Thiesen B, et al. Thermotherapy of prostate cancer using magnetic nanoparticles: feasibility, imaging, and three-dimensional temperature distribution. European urology. 2007;52(6):1653–1662.
9. Dobson J. Magnetic nanoparticles for drug delivery. Drug development research. 2006;67(1):55–60.
10. Maier-Hauff K, Rothe R, Scholz R, et al. Intracranial thermotherapy using magnetic nanoparticles combined with external beam radiotherapy: results of a feasibility study on patients with glioblastoma multiforme. Journal of neuro-oncology. 2007;81(1):53–60.
11. Najdahmadi A, Lakey JR, Botvinick E. Structural Characteristics and Diffusion Coefficient of Alginate Hydrogels Used for Cell Based Drug Delivery. MRS Advances. 2018:1–10.
12. Goudarzi HM, Yarahmadi M, Shafii MB. Design and construction of a two-phase fluid piston engine based on the structure of fluidyne. Energy. 2017;127:660–670.
13. Orekhova N, Akchurin R, Belyaev A, et al. Local prevention of trombosis in animal arteries by means of magnetic targeting of aspirin-loaded red cells. Thrombosis research. 1990;57(4):611–616.
14. Stoimenov PK, Klinger RL, Marchin GL, et al. Metal oxide nanoparticles as bactericidal agents. Langmuir. 2002;18(17):6679–6686.
15. Gong P, Li H, He X, et al. Preparation and antibacterial activity of Fe3O4@ Ag nanoparticles. Nanotechnology. 2007;18(28):285604.
16. Dougherty TJ, Gomer CJ, Henderson BW, et al. Photodynamic therapy. JNCI: Journal of the National Cancer Institute. 1998;90(12):889–905.
17. Gao ZG, Fain HD, Rapoport N. Controlled and targeted tumor chemotherapy by micellar-encapsulated drug and ultrasound. Journal of Controlled Release. 2005;102(1):203–222.
18. Loghmannia P, Kamyab M, Nikkhah MR, et al. Miniaturized low-cost phased-array antenna using SIW slot elements. IEEE Antennas and Wireless Propagation Letters. 2012;11:1434–1437.
19. Allen E, Burdette J. Questions and Answers in MRI. St. Louis, MO: Mosby. 2nd ed. by University of Maryland-College Park on. 2001;7(14):14.
20. Schenck JF. Safety of strong, static magnetic fields. Journal of magnetic resonance imaging. 2000;12(1):2–19.
21. Andersen E. Magnetic resonance imaging—safety and health issues. Aaohn Journal. 2007;55(4):137–139.
22. Pirbazari PM, Kisomi BF. Co/TiO2 nanoparticles: preparation, characterization and its application for photocatalytic degradation of methylene blue. Desalin, Water Treat. 2017;63:283–292.
23. Goodwin S, Peterson C, Hoh C, et al. Targeting and retention of magnetic targeted carriers (MTCs) enhancing intra-arterial chemotherapy. Journal of Magnetism and Magnetic Materials. 1999;194(1):132–139.
24. Chertok B, Moffat BA, David AE, et al. Iron oxide nanoparticles as a drug delivery vehicle for MRI monitored magnetic targeting of brain tumors. Biomaterials. 2008;29(4):487–496.
25. Sun C, Lee JS, Zhang M. Magnetic nanoparticles in MR imaging and drug delivery. Advanced drug delivery reviews. 2008;60(11):1252–1265.
26. Nacev A, Beni C, Bruno O, et al. The behaviors of ferromagnetic nano-particles in and around blood vessels under applied magnetic fields. Journal of magnetism and magnetic materials. 2011;323(6):651–668.
27. Nacev A, Beni C, Bruno O, et al. Magnetic nanoparticle transport within flowing blood and into surrounding tissue. Nanomedicine. 2010;5(9):1459–1466.
28. Karimi M, Solati N, Ghasemi A, et al. Carbon nanotubes part II: a remarkable carrier for drug and gene delivery. Expert opinion on drug delivery. 2015;12(7):1089–1105.
29. Malekzad H, Mirshekari H, Sahandi Zangabad P, et al. Plant protein-based hydrophobic fine and ultrafine carrier particles in drug delivery systems. Critical Reviews in Biotechnology. 2017:1–21.
30. Najdahmadi A, Lakey JR, Botvinick E. Diffusion coefficient of alginate microcapsules used in pancreatic islet transplantation, a method to cure type 1 diabetes. Nanoscale Imaging, Sensing, and Actuation for Biomedical Applications. 2018.
31. Yarahmadi M, Goudarzi HM, Shafii M. Experimental investigation into laminar forced convective heat transfer of ferrofluids under constant and oscillating magnetic field with different magnetic field arrangements and oscillation modes. Experimental Thermal and Fluid Science. 2015;68:601–611.
32. Takeda Si, Mishima F, Fujimoto S, et al. Development of magnetically targeted drug delivery system using superconducting magnet. Journal of Magnetism and Magnetic Materials. 2007;311(1):367–371.
33. Rotariu O, Strachan NJ. Modelling magnetic carrier particle targeting in the tumor microvasculature for cancer treatment. Journal of Magnetism and Magnetic Materials. 2005;293(1):639–646.
34. Holligan D, Gillies G, Dailey J. Magnetic guidance of ferrofluidic nanoparticles in an in vitro model of intraocular retinal repair. Nanotechnology. 2003;14(6):661.
35. Alexiou C, Diehl D, Henninger P, et al. A high field gradient magnet for magnetic drug targeting. IEEE Transactions on applied superconductivity. 2006;16(2):1527–1530.
36. Ally J, Martin B, Khamesee MB, et al. Magnetic targeting of aerosol particles for cancer therapy. Journal of Magnetism and Magnetic Materials. 2005;293(1):442–449.
37. Dames P, Gleich B, Flemmer A, et al. Targeted delivery of magnetic aerosol droplets to the lung. Nature nanotechnology. 2007;2(8):495–499.
38. Lübbe AS, Bergemann C, Huhnt W, et al. Preclinical experiences with magnetic drug targeting: tolerance and efficacy. Cancer research. 1996;56(20):4694–4701.
39. Arruebo M, Fernández-Pacheco R, Ibarra MR, Santamaría J. Magnetic nanoparticles for drug delivery. Nano today. 2007;2(3):22–32.
40. Okuhata Y. Delivery of diagnostic agents for magnetic resonance imaging. Advanced drug delivery reviews. 1999;37(1):121–137.
41. Decuzzi P, Pasqualini R, Arap W, Ferrari M. Intravascular delivery of particulate systems: does geometry really matter? Pharmaceutical research. 2009;26(1):235.
42. Fournier RL. Basic transport phenomena in biomedical engineering. CRC press; 2017.
43. Hobbs SK, Monsky WL, Yuan F, et al. Regulation of transport pathways in tumor vessels: role of tumor type and microenvironment. Proceedings of the National Academy of Sciences. 1998;95(8):4607–4612.
44. Saltzman WM. Drug delivery: engineering principles for drug therapy. Oxford University Press; 2001.
45. Faraji S, Yardim MF, Can DS, et al. Characterization of polyacrylonitrile, poly (acrylonitrile‐co‐vinyl acetate), and poly (acrylonitrile‐co‐itaconic acid) based activated carbon nanofibers. Journal of Applied Polymer Science. 2017;134(2).
46. Faraji S. Polimerlerden Aktif Karbon Nano-fiber Oluşturma, Fen Bilimleri Enstitüsü.
47. Lübbe AS, Alexiou C, Bergemann C. Clinical applications of magnetic drug targeting. Journal of Surgical Research. 2001;95(2):200–206.
48. Lübbe AS, Bergemann C, Brock J, McClure DG. Physiological aspects in magnetic drug-targeting. Journal of Magnetism and Magnetic Materials. 1999;194(1):149–155.
49. Rosensweig R. Directions in ferrohydrodynamics. Journal of Applied Physics. 1985;57(8):4259–4264.
50. Diver DA, Lubbe AS. Control to concentrate drug-coated magnetic particles to deep-tissue tumors for targeted cancer chemotherapy. Decision and Control, 2007 46th IEEE Conference on 2007. 2007.
51. Mikkelsen CI. Magnetic separation and hydrodynamic interactions in microfluidics. 2005.
52. Forbes ZG, Yellen BB, Barbee KA, Friedman G. An approach to targeted drug delivery based on uniform magnetic fields. IEEE Transactions on Magnetics. 2003;39(5):3372–3377.
53. Polyak B, Fishbein I, Chorny M, et al. High field gradient targeting of magnetic nanoparticle-loaded endothelial cells to the surfaces of steel stents. Proceedings of the National Academy of Sciences. 2008;105(2):698–703.
54. Yellen B, Forbes Z, Barbee K, Friedman G. Model of an approach to targeted drug delivery based on uniform magnetic fields. . INTERMAG 2003. 2003.
55. Zheng J, Wang J, Tang T, et al. Experimental study on magnetic drug targeting in treating cholangiocarcinoma based on internal magnetic fields. The Chinese-German Journal of Clinical Oncology. 2006;5(5):336–338.
56. Furlani E, Ng K. Analytical model of magnetic nanoparticle transport and capture in the microvasculature. Physical review E. 2006;73(6):061919.