The simple model of grain and phase boundaries diffusion into polycrystalline solid system with nano- and micro grain dimensions is proposed. There are considered different types of diffusion regimes which are realized by definite correlations between volume and grain boundary diffusion lengths and average grain sizes. The study shows the temperature regimes where the diffusion along triple junctions is the control stage of structural processes in metal materials.

Keywords: metal materials, solid polycrystalline, diffusion, nano, polycrystalline

Let us consider the process of propagation of diffusing atoms in a solid polycrystalline metal system. The diffusion at relatively low temperatures is of particular interest under the circumstances where the bulk diffusion coefficient is small, and most of the diffusion flow is carried along interfaces (grain boundaries) and linear lattice defects. If we are dealing with a microcrystalline or nanocrystalline system, i.e. if the average grain size d is not more than one micrometer, then the grain boundaries (and also the inter phase boundaries in a multiphase metal system) and the triple junctions must be considered as accelerated paths of low-temperature diffusion. It has been well-established that at temperatures below 0.7T_m (T_m stands for the melting temperature of the system being studied) the grain boundary self-diffusion¹ and hetero-diffusion² coefficients are 10³–10⁵ times bigger than the bulk diffusion coefficients. It is shown in³ that at even lower temperatures (T≈0.55÷0.6T_m) the diffusion penetration rate through triple junctions is over a thousand times higher than the diffusion rate along grain boundaries.

Let us choose the following conditions for description of a low-temperature diffusion process in a polycrystalline solid. Suppose the temperature (and the observation time) corresponds to the diffusion path of bulk diffusion $L_V=2{\left(D_{V}t\right)}^{1/2}$ (D_V is the bulk diffusion coefficient) which does not exceed the width of the grain boundaries - δ. This equates to the C mode of the grain boundary diffusion according to the Harrison classification,⁴ which means that bulk diffusion can be disregarded in the total balance of diffusion flows. Additionally, let us consider that at the given external conditions $D_T>>D_B,D_B$ – diffusion coefficient along the grain boundaries (its value is the same for all grain boundaries), D_T – diffusion coefficient along triple boundary junctions (its value is also the same for all triple junctions). In such a way, the advance diffusion of diffusing atoms occurs along triple junctions with substance outflow to the grain boundaries; the diffusion from grain boundaries to the grain bulk is not considered. Figure 1 shows a simple scheme of a network of triple junctions which are parallel to each other in two orthogonal directions – along the y and x axes.

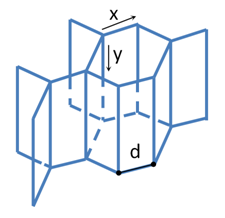
Figure 1 Triple junctions network in the polycrystalline solid-state system ;⁷ axes x - directions of grain boundaries that spreading from each triple junction (y axes) in a perpendicular plane.

The distances between the lines of triple junctions parallel to the y axis are equal to d; let us use the value of d as an estimation of the average grain size in the sample. The source of the diffusing substance is located on the sample’s surface (y = 0) and has a constant concentration c₀. The diffusion flow along triple junctions is directed along the y axis. The high transfer rate along triple junctions and the ratio of grain size d to the sample size l (d << l), allows us to ignore redistribution of the diffusing substance between triple junctions that are directed from the diffusion source into the sample depth (along the y axis) in transverse directions perpendicular to the y axis. It can be assumed that a single diffusion front exists along triple junctions whose distance from the source surface is determined by the diffusion path along triple junctions – L_T. The triple junction inside each grain layer along which the diffusing substance spreads is the diffusion source for the three grain boundaries "belonging" to this junction. Meanwhile, the sources of the diffusing substance for each of these three boundaries are two adjacent triple junctions (Figure 2).

According to the proposed scheme, the model of the diffusion process can be represented as follows:

$\frac{\partial c_T}{\partial t}=D_T\frac{{\partial }^2{c}_T}{\partial y^2}+\frac{3}{\delta }{D}_B\frac{\partial c_B}{\partial x}|{}_{x=\pm \frac{\delta }{2}}$    (1)

$\frac{\partial c_B}{\partial t}=D_B\frac{{\partial }^2{c}_B}{\partial x^2}$                     (2)

where c_T and c_B – the concentration of the diffusing substance in the triple junction (TJ) and the grain boundary (GB) respectively. This model is appropriate for describing self-diffusion. It can however be used for hetero diffusion as well, assuming that the diffusing substance distribution coefficient between TJ and GB is equal to 1. This model is an extension of the Fisher model⁵ for grain boundary diffusion. Depending on the ratio of two parameters (the grain boundary diffusion path L_B and the average grain size d) different variants of considering this diffusions problem are possible.

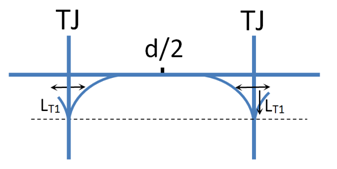
Figure 2 The spread of diffusing atoms in nearby triple junctions and grain boundaries.⁷

 Variant 1

$L_B/d<<1–$ a diffusion model along individual independent TJ with substance outflow to GB. It can be assumed in this variant that the grain boundary diffusion path is so much less than the grain size that the concentration in GB in the middle of the distance between TJs falls to zero $c_B\left(x=d/2,y,t\right)$  = 0. The initial and boundary conditions will then be as follows: $c_B\left(x,y,t=0\right)=0$ , $c_B(x=\pm \delta /2,y,t)=c_T$ . If, following Fisher, we assume that , then the concentration in GB is determined by the equation (2)

$c_B\left(x,y,t\right)=c_T\left(y,t\right)erfc\left(x/2{\left(D_{B}t\right)}^{1/2}\right)$      (3)

The expression for concentration in each TJ can be obtained from the equation (1); in a quasi-stationary case, it will take the form

$c_T(y,t)=c_0\exp \left[-\frac{y}{L_{T_1}}\right]$                                                       (4)

where the diffusion path along the triple junction, or, equivalently, the average position of the diffusion front depth along individual TJs, is described by the expression

$L_{T_1}={\left(\frac{D_T\delta \sqrt{\pi t}}{3\sqrt{D_B}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$                                                                                              (5)

Variant 2

$L_B/d>1/2–$ a diffusion model in a single system of connected triple junctions and grain boundaries. The diffusion flows in this option from the adjacent TJs to GB collide and overlap. The solution of equation (2) for the diffusion in GB corresponds to the solution of the problem of diffusion in a plate, and has the form

$c_B(x,y,t)=c_T(y,t)\left(1-\frac{4}{\pi }\exp (-\lambda \right)\sin \frac{\pi x}{d}$                                         (6)

where $\lambda =\frac{{\pi }^2{D}_{B}t}{d^2}$

The solution of equation (1) in a quasi-stationary approximation gives an expression similar to the equation (4)

$c_T(y,t)=c_0\exp \left[-\frac{y}{L_{T_2}}\right]$                                                      (7)

however, the diffusion path (the diffusion front position in the system of connected TJs) $L_{T_2}^B$ is different from $L_{T_1}$

$L_{T_2}={\left(\frac{D_T\delta d}{12D_B}{e}^{\lambda }\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$                                            (8)

The depth to which the diffusing substance penetrates along the system of connected TJs depends not only on TJ diffusive permeability (D_T) and GB diffusive permeability (D_B), but on the average grain size d in the sample. According to the equation (8), the distance of the diffusion front in the connected TJ system from the outer surface which is the diffusion process source in a polycrystalline sample increases with decreasing d. This variant has another peculiarity. Isoconcentration lines in each GB fall from TJs to the middle distance between TJs, i.e. at $x=d/2$ (Figure 3). When $x=d/2$ , the concentration in GB is minimal. Using the equations (6, 7) it is possible to find the distance from the outer surface to the concentration minimum in GB, provided that the isoconcentration line corresponds to the concentration equal to the concentration in TJ at the depth $L_{T_2}$ (i.e. it corresponds to the concentration in the diffusion front in the connected TJ system). Let us denote this distance $L_{T_2}^B$ , which means that this is the diffusion path in GB (the superscript), formed due to advance diffusion along TJ (the subscript), which are the sources of filling GB with the diffusing substance. Its value can be determined by the formula

$L_{T_2}^B=L_{T_2}\left[1+\ln \left(1-\frac{4}{\pi }{e}^{-\lambda }\right)\right]$                   (9)

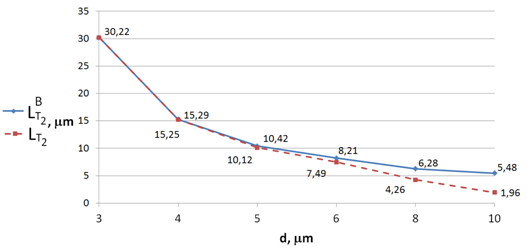
The diffusion path $L_{T_2}^B$ , which has the same value for the considered external conditions in all GB of the sample, means the diffusion front along GB. With decreasing average grain size, the distance between the diffusion front along TJ and the diffusion front along GB diminishes (Figure 4). In order to demonstrate the dependence of the penetration depth of the substance diffusing into a polycrystalline solid on grain size, let us consider an example of low-temperature diffusion in a real binary system. Let us choose the Al-Zn system for this purpose, for which the bulk and grain boundary diffusion coefficients of zinc in aluminum are well known over a broad temperature range;⁶ and the value of the coefficient of zinc diffusion along the triple grain junction in a polycrystalline aluminum sample has been experimentally determined.³ For calculation of zinc penetration depth along triple junctions $L_{T_2}$ and along grain boundaries $$L_{T_2}^B$$ , a temperature should be chosen that corresponds to an almost total absence of bulk diffusion, i.e. to the C mode of grain boundary diffusion according to Harrison. According to the diffusion data in the literature, an estimation of the bulk diffusion path of zinc in aluminum at 50^oС during 10 minutes gives L_V=4·10^-11m (0.04nm), which corresponds to the C mode. The grain boundary diffusion coefficient at this temperature is $D_V=1.66·{10}^{-14}{m}^2/s$ , and the grain boundary diffusion path is $L_B=6.3·{10}^{-6}m$ (6.3mm). Let us assume that the D_T /D_B ratio in this case is not less than 10⁴ according to.⁶ The GB thickness and transverse TJ size are taken to be 5·10^-10m. On the basis of these numerical data and using the formulas (8, 9), let us calculate $L_{T_2}$ and $L_{T_2}^B$ for the average grain size from 10 to 2mm. The calculation data are presented in the table and in the chart (Figure 4).⁷

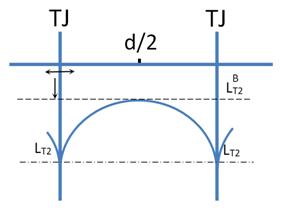
Figure 3 The position of the diffusion fronts in triple junctions and grain boundaries in the related triple junctions model.⁷
– – – – - diffusion front along the grain boundaries.
–·–·–· - diffusion front along the triple junctions.

Figure 4 Zn diffusion depth in polycrystalline Al depending on the average grain size d.⁷
 - Diffusion depth along the triple junctions.
 - Diffusion depth along the grain boundaries.

Therefore, if the grain size in the polycrystalline solid is comparable with the diffusion path along GB, two diffusion fronts are formed in the sample with diffusing substance propagation. The first is the diffusion front along TJ, the second – the diffusion front along GB, which is also formed due to a rapid transfer of the substance along TJs. When decreasing grain size, the penetration depth along TJ and GB increases ($L_{T_2}$ and $L_{T_2}^B$ increase), and both fronts converge. This means that the total depth of the diffusing substance penetration into a sample increases with decreasing average grain size (at constant external conditions). At relatively low temperatures, a small-grained material becomes more permeable to diffusion than a large-grained material. A diffusing substance penetrates into it to a greater depth, and the material is saturated more. This examination shows the temperature regimes where the diffusion along triple junctions is the control stage of structural processes in metal materials.

None.

Authors declare that there is no conflict of interest.

1. Bokshtein BS. Diffusion in Metals. Moscow: Metallurgiya. 1978.
2. Aleshin AN. Relations between the parameters of grain-boundary diffusion of zinc in aluminum. Metally. 2006;2:150‒153.
3. Bokstein BS, Ivanov VA, Oreshina OA, et al. Direct experimental observation of accelerated Zn diffusion along triple junctions in Al. Mater Sci Eng. 2001;302:151.
4. Bokshtein BS, Kopetskiy Ch V. Thermodynamics and kinetics of grain boundaries in metals. Metallurgiya. 1986:224.
5. Fisher JC. Calculation of Diffusion Penetration Curves for Surface and Grain Boundary Diffusion. Journal of applied physics. 1951;22(1):74.
6. Aleshin AN. Diffusion in an ensemble of intersecting grain boundaries forming a triple junction. Metally. 2009;5:394–399.
7. Petelin A, Apykhtina I, Novikov A, et al. Model description of grain boundary diffusion processes in microcrystalline solid systems. Mater Sci Non-Equilibrium Phase Transformations. 2018;4(3):89‒91.