This report comprises an outline of an experimental setting intended to provide insight into statistical concepts of great interest for engineering and science students. The main components of a DC voltage source are presented alongside measurements of voltage and current behaviours on the system with their corresponding uncertainties, and a brief statistical analysis of the data thereby obtained. It also encompasses a brief discussion on the influence of the measuring device on reported resistance values and provides experimental insight into Ohm’s law via regression analysis. Under the study of both DC voltages and direct currents, a typical example of a circuit is used to develop clear-cut methods relating to statistical treatments of regression and both direct- and indirect-measurement uncertainties.

Keywords: statistical concepts, voltage, power, engineering, current, electronics, circuit laws

Voltage sources are devices commonly used in engineering that primarily rely on the operation of diode bridges and voltage- smoothing capacitors (as it shall be presented in subsequent sections). They naturally abide by the laws of electromagnetism, and therefore exhibit some of the most pivotal phenomenological relations in the realm of electrodynamics as applied to electronics, among which Ohm’s law is perhaps the most well-known —for a thorough discussion thereof, see.¹ A behavioral analysis of both input and output voltage signals in such a circuit can thus provide enlightening information on the statement of basic circuit laws from a purely, and thoroughly applied, experimental setting.² The aim of this report is to use the construction of a voltage source as a means for grasping concepts in connection to statistics and experimental data treatment in engineering and natural sciences courses. The significance thereof lies in the fact that it reconciles an experimental setting with the theoretical assimilation of statistical concepts such as variance, standard deviation, mean, confidence intervals, along with specific inferential methods, namely, that of linear regression. This allegedly motivates and eases the learning process.

Description of the system

A power supply comprising an electrical power transformer whose signal was filtered through a common circuit, known as full-wave bridge rectifier, was studied; in principle, such devices make use of both half cycles issued by an alternating-current (AC) emf source —i.e., the transformer— and convert them to direct-current (DC) voltage.³ The aforementioned conversion is based on a special configuration of four diodes, frequently referred to as a “bridge”. Figure 1 provides a representation of this mounting.⁴ As seen in Figure 1, the load voltage may be filtered through a smoothing capacitor connected across the resistor; this yields a pulsating, yet not completely dying out voltage. A brief justification for the above fact can be presented on account of the following mechanism: to begin with, the capacitor charges during the first quarter cycle, ideally until attaining a voltage equivalent to 0; immediately afterwards, the emf provided by the source be- gins to decrease, so that the voltage upon the capacitor becomes greater in comparison to it. Since V_capacitor>V_source, and charges cannot move from a region of less voltage to a region of greater voltage, there cannot be flowing charges through the diodes at such moments.³ Thus the load current is supplied by discharge of the capacitor until the emf issued by the source reaches another peak; this process is illustrated in Figure 2. Finally, the implemented circuit also contains an LM317 series terminal-adjustable regulator, which, according to the device’s spe- cifications,⁵ is capable of supplying more than 1:5 A over an output-voltage range from 1:25 V to 37 V. It requires only two external resistors to set the output voltage.

Figure 1 Full-wave bridge rectifier; input AC-emf is provided by a transformer.

Figure 2 Rectified load voltage, smoothed with a capacitor.

The power supply was mounted on a breadboard with a W04M full wave bridge rectifier,⁶ a 2200µF electrolytic capacitor, and a 5k▲ potentiometer. The source of emf for the transformer was typical mains electricity, which is locally reported to be around 120V RMS,⁷ but was measured at the time of performing the experiment as .126:6 ˙ 0:2/V RMS. In the beginning of the statistical analysis, uncertainties bound to the taken measurements were carefully pondered, for they comprised one of the major considerations as far as presentation of results was concerned; a Fluke 87V multi-meter was used to measure both current and voltage. According to the multimeter’s features,⁸ uncertainties are given by Table 1. By dint thereof, it can be estimated that, if h D order of magnitude of least significant figure/, then

Direct current: $\delta \overline{V}=\overline{V}.\frac{0.05}{100}+\lambda$

Alternate current: $\delta \overline{V}=\overline{V}.\frac{0.01}{100}+2.\lambda$

$\delta \stackrel{-}{{\displaystyle i}}=\{\frac{\stackrel{-}{{\displaystyle i}}.\frac{0.2}{100}+4.\lambda , if\stackrel{-}{{\displaystyle i}}{\rm E}[0,60]}{\stackrel{-}{{\displaystyle i}}.\frac{0.2}{100}+2.\lambda , if\stackrel{-}{{\displaystyle i}}{\rm E}[60,400]}$

$\delta R=\{\frac{R.\frac{0.2}{100}+2.\lambda , ifR{\rm E}[0,600]}{R.\frac{0.2}{100}+\lambda , ifR{\rm E}[600,6000]}$

In connection therewith is, of course, the assessment of the correctness of the theory described above, since measuring the amount of voltage on some of the electronic components present in the arrangement turns out to be necessary for said purpose. The used transformer, an ELA Elektrotechnik type UI 39/17, ideally provides a sinusoidal emf of nearly 24 V RMS1, yet it was measured to be.23:28 ˙ 0:02/V; on the grounds p that the RMS voltage for a sinusoidal wave satisfies VRMS D E₀= 2, an expected value for E0 may be computed, which must be close to the measured voltage value

On the capacitor and, accordingly, on the rest of the circuit up to the regulator. If the voltmeter had an appreciable effect on the circuit’s voltage, it would be expected that load voltage readings dropped off with respect to the theorized value, for it would effectively add an extra parallel resistor to the output connection, thus producing a slightly lower total load resistance on the source:

R_load = RR_v/R+R_v<R(Two parallel resistors),

with RV representing the voltmeter’s resistance. In fact, the only way in which such an expression is exactly equal to the used and known resistance R is by considering, instead, lim R_load.  As for current readings, since the connection is made serially, the internal voltmeter resistance would yield an accumulated load resistance.

R_load = R+R_v>R

which in turn would reduce the current through the circuit. Therefore, in this case, a voltmeter is expected to have a behaviour resembling lim R_load.

Firstly, it must be pointed out that an applied linear regression model of the form Y= βX requires reckoning the validity of five hypotheses, which may be referred to as inference conditions from this point onwards. Obviously, there ought to be a linear relationship between X and Y values, for the study of which a set of essentially random data points is chosen; but there must also be mutual independence in the set, in the sense that each individual observation must be completely unbound to the other ones, i.e., a certain data point should be unaltered whenever some other point is removed or changed in any way. Most importantly, it is assumed that the probability density function describing possible Y values for a fixed parameter X is normal; furthermore, it is supposed that the set of normal distributions of Y ’s has equal variance.  In terms of regression analysis, it is essential to note that any reported value of y —which stands for an estimation of β— must be within a confidence interval, ordinarily interpreted⁹ as an interval estimate for a value of the form (γL, γU). Where γL  and γU are functions of the selected sample, so that the interval has a specified probability of containing the true value of an unknown constant γ. In simple terms, it is assumed that a linear model Y= βX in which all inference conditions are met, provides an estimate y  for the coefficient of a “real” parameter relating with the whole population, namely β; such estimators $\stackrel{\wedge }{\beta }$ ’s are assumed to be normally distributed, and fitting a regression model provides too an estimate of their standard deviation. Since the standard deviation of the distribution is not actually known, but rather an estimation thereof, it is mandatory to use a t -distribution to compute confidence intervals. On those grounds, it is stipulated —in fact, as it is done in¹⁰ —that the formula for a 100(1-α) confidence interval is

$(\stackrel{\wedge }{\beta }-\stackrel{\wedge }{\sigma }t\alpha /2;n-2,\stackrel{\wedge }{\beta }+\stackrel{\wedge }{\sigma }t\alpha /2;n-2$

where n—2 is used as the degrees of freedom of the model, and $\stackrel{\wedge }{\sigma }$ represents the estimated standard error. The above procedure does not in any sense mean that the error can be treated in a somewhat arbitrary manner, but it enhances the multiple possible ways in which a result may be treated and reported. Certainly, reducing the probability by which one wishes to find the studied value yields a much more precise expression (viz. a “smaller” interval), but it reduces the significance thereof by implying greater uncertainty on whether the reported value is, in point of fact, reasonable. According to the discussion found in,¹¹ the amount of significant figures used for reporting the regression coefficient is given by consideration of the value

$\sqrt{\frac{1}{2n-2}}.\stackrel{\wedge }{\sigma };$

and so, the amount of significant decimal digits to be used is given by the amount of zero decimal places in this value. As a matter of fact, the above value corresponds in our case to the recommendation given by,¹² that no more than two significant places be used for the uncertainty in regression coefficients. After all the measurements were carried out, it could be seen that the voltage on the capacitor was (32.20±0:03) V, in contrast with the theorized value of (32.92±0:03)V, which was obtained —as seen in the previous section— by multiplying the measured RMS from the transformer’s secondary by the value $\sqrt{2}$ (the uncertainty must then be scaled by the same factor). This measurement of voltage has a relative error, with respect to the theoretical value, of nearly 5%; such deviation is presumably due to the fact that the circuit is not totally conductive, as it is assumed to be in theory. The 0-resistance hypothesis remains, nevertheless, relatively sound. Besides, it was found that, for two different load resistance values of (228:1±0:7) and (1:076±0:003) kΩ, the output range of the source was from (1:236±0:002) V to (27:80±0:02)V and from (1:236±0:002)V to (27:75±0:02)V, respectively. Now, the data that was gathered from the experiment, namely, the values of voltage and current on certain load resistor values, was processed into python, program with which the graphs in Figure 3 could be drawn. These lines represent two particular estimation cases for the linear equation V = βi, where β  stands for the resistance in the assessed section of the circuit. Each case sets up a verification of the statement of Ohm’s law, and most importantly for an estimation of the load resistance.

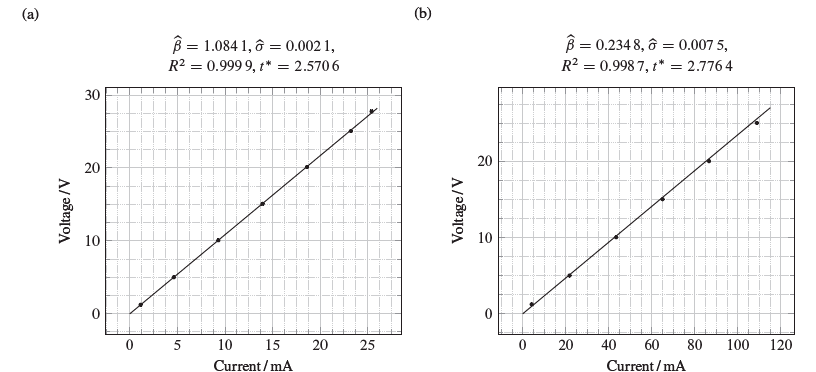
Figure 3 Adjusted linear models for two different load resistor values, t* parameters are calculated within a 95% confidence interval. (A) Arrangement with a load resistor of (1:076±0:003) kΩ. (B) Arrangement with a load resistor of (228:1±0.7)Ω.

From Figure 3, it is seen that a straightforward computation of Ohm’s law yields a reasonably good approximation to the actual load resistor values in each case. Indeed, the value of resistance in Figure 3A can be presented within a 95% confidence interval, by cause of what has been said about the regression, as

(1:084±0:005) VmA^-1 = (1:084 ±0:005/) kΩ (0:5 % relative error)

correspondingly, Figure 3B can be taken to yield a theorised resistance value of

(0:23±0:02) VmA^-1 = (230±20) Ω (8:7% relative error). 

(a 95% confidence interval is, for the sake of current objectives, a good enough estimation for the parameter.) On the grounds that these values have relative errors of 0:3% and 0:9% (respectively), with respect to the actually measured ones, it may well be concluded that the expression of Ohm’s law describes on an accurate manner the reality of the load current, voltage, and resistance in the studied case, regardless of the presence of the measuring device. Hence it should be expected, by virtue of the obtained results, that the resistance of the used tool is much higher than that of the known resistor, there by being negligible with respect to the reported voltage readings; and a very low resistance is likewise expected for current measurements. In point of fact, these conclusions are in accordance with what has been proposed and shown by other works,¹³ inasmuch as it has been claimed that typical digital multimeters offer an effective resistance of nearly 10 MΩ on load circuits. Likewise, the aforementioned claim is supported by what can be drawn from the multimeter’s manual,¹⁴ considering that it reports a 10MΩ value for the multimeter’s resistance in measuring DC voltages. On the other hand,¹⁴ specifies a “burden voltage” of 1:8mVmA^-1 (which is to say, a resistance of 1:8Ω) in current readings ranging up to 400:0mA; therewith it is seen that the maximum current reading (of about 110mA), corresponding to the maximum voltage drop across the voltmeter, caused a voltage of 198mV through its connection, and considering that the total voltage on the circuit load was about 25V, that voltage drop accounted for only 0:8 % of the total voltage.

Generally speaking, a significant resistance value by the multimeter could potentially shrink the gradient of the curve (if the decrease of current values is less than that of voltage), or it could enlarge it (if the decrease of current values is greater than those of voltage). However, and in keeping with what has been measured, no significant difference was appreciated with regard to the theoretical value considering R alone. This suggests either a uniform reduction in the readings of both parameters or a nearly ideal behaviour of the device’s resistance; although the latter is a notably more plausible hypothesis, it remains out of the scope of this report to decide whether it is indeed the case. By means of what has been herein presented, it is a straightforward matter to recognise that the influence, in terms of resistance, of the measuring device on the circuit is remarkably negligible with respect to voltage and current manipulations. Additionally, it has been proven that the theoretical model upon which the operation of the source relies is coherent with the reported measurements, and that the LM317 regulator provides an outstandingly stable voltage output range, at least for load resistors within orders of magnitude ranging from 100Ω to 1000Ω. In addition, the construction and analysis of the elements that constitute a voltage source enabled us to make use of significant statistical concepts (such as distribution functions, variance, relative error, etc) in a pragmatic framework.

None.

The authors declare that there is no conflict of interest.

1. Griffiths DJ. Introduction to electrodynamics. Prentice Hall New Jersey.1962.
2. Pejovic P, Kolar JW. Single-Phase Full-Wave Recti- fier as an Effective Example to Teach Normalization, Con- duction Modes, and Circuit Analysis Methods. Electronics. 2013;17:123–129.
3. Mehta V, Mehta S. Principles of electronics. S Chand & Co Ltd; 2008.
4. Plonus M. Electronics and communications for scientists and engineers. Butterworth-Heinemann. 2020.
5. 3-Terminal Adjustable Regulator, LM317. Texas Instru- ments. 2021.
6. Single-phase glass passivated silicon bridge rectifier, W04M, Rectron Semiconductor. 2001.
7. Ministerio de minas y energía de Colombia, Resolución 90708: Reglamento Técnico de Instalaciones Eléctricas – RETIE. 2013.
8. Fluke 83V and 87V Digital Multimeters, Detailed Specifica- tions. Fluke Corporation; 2005.
9. Dekking FM, Kraaikamp C, Lopuhaä HP, et al. A Modern Introduction to Probability and Statist- ics: Understanding why and how. Springer Science & Busi- ness Media; 2005.
10. Dudgeon P. A Comparative Investigation of Confidence Intervals for IndependentVariables in Linear Regression. Multivariate Behavioral Research. 2016;51:139–153.
11. Squires GL. Practical physics. Cambridge University Press; 2001.
12. Hughes I, Hase T. Measurements and their uncertain- ties: A practical guide to modern error analysis. Oxford Uni- versity Press; 2010.
13. Stojilovic N, Isaacs DE. Resistance of a digital volt- meter: teaching creative thinking through an inquiry-based lab. Physics Education. 2018;53:053005.
14. 80 Series V Multimeters Users Manual. Fluke Corporation; 2004.