Oxide semiconductor SnO₂ shows excellent photoelectronic properties and sensitivities of gases. It is known that their special properties are originated by a stable large band-gap. In nano-SnO₂, the above properties have been extensively explored, and nano-SnO₂ will find wide applications in microelectronics, photoelectronics, sensor and compound function ceramics. According to our study using group theory, a single SnO₂ crystal with rutile-type structure shows four Raman active modes, A _1g, B _1g, B _2g and E _g. The additional A _2μ and E _μ modes correspond to transverse-optical (TO) and longitudinal-optical (LO) vibrations. Moreover, we applied application of perturbation theory, consequently, the spectrum of commercial SnO₂ sample showed the Raman bands in accordance with the theory.

Keywords: group theory, SnO₂

The unique structure and unique physical and chemical properties of nanomaterials have recently attracted a lot of attention. In general, nanostructured materials are composed of crystal grain components including nanocrystalline, nanocluster assemblies, and nano amorphous particles, and interface components formed by large interfaces and surfaces.^1-4 Interface and surface structure have been widely studied until recently. Various types of interfacial structural models have been proposed for gas-like models, order and extended order models, and nanostructured materials. Distribution of structural characteristics Various intrinsic characteristics of nanomaterials are described in terms of interface and surface structure, while the effect of the internal microstructure of the particles is generally neglected. In fact, in other manufacturing methods, the microstructure of the nanomaterial may be nanocrystals, nanocrystalline particles, or a nanocluster assembly with some crystal characteristics. Since particles are basic components of nanomaterials, changes in internal microstructure inevitably change physical and chemical properties. Therefore, research on the microstructure inside the particles can help clarify the general structure of nanomaterials and explain the corresponding experimental results.^5,6

X-ray diffraction is a powerful tool commonly used to study the structure of materials. For nanomaterials, XRD is used to determine the crystal structure, and it is common to approximately estimate the average particle size including a change in particle size according to the annealing temperature. Looking at trends over the past few years, there have been several papers reporting the use of XRD for a more detailed study of lattice distortion of nanomaterials and changes in microstructure according to annealing temperature. Raman spectroscopy, on the other hand, is a powerful tool used to illuminate the spatial symmetry of matter. XRD and Raman’s use spectroscopy can enhance our understanding of the microstructure changes in nanomaterials and signals from various defect states.^7-9

SnO₂ is a stable large bandgap oxide semiconductor with excellent photoelectronic properties and sensitivity such as gas. The aforementioned properties in NanoSnO₂ have been extensively studied, and NanoSnO₂ will find a variety of applications in microelectronics, optoelectronics, sensors, and composite functional ceramics. Attempts to improve the properties rely primarily on an understanding of the microstructure of nano SnO₂. In this study, we studied the relationship between microstructure changes. Changes in particle and spatial symmetry and causes of lattice distortion according to the annealing temperature of nano SnO₂ were discussed.^10,11

Various physical systems such as crystals and individual atoms can be modeled by symmetric groups. Thus, expression theory, which is closely related to group theory, has many important applications in physics, chemistry, and material science. Group theory is also the core of public key encryption.^12,13 In physics, a group is important because it describes the symmetry with which the laws of physics seem to follow. According to Noeter’s theorem[?], every successive symmetry of a physical system corresponds to the conservation law of a system. Group theory can be used to address the incompleteness of the statistical interpretation of dynamics developed by Willard Gibbs, which relates to the sum of infinite probabilities to yield meaningful solutions.

In chemistry and material science, point groups classify the symmetry of tetrahedrons and molecules, while space groups are used to classify crystal structures. Assigned groups can be used to determine physical properties, spectroscopic properties (especially Raman spectroscopy, infrared spectroscopy, circular spectroscopy, magnetic circular spectroscopy, UV/Vis spectroscopy, fluorescence spectroscopy) and construct molecular orbitals.

Molecular symmetry is responsible for many physical and spectroscopic properties of compounds and provides relevant information on how chemical reactions take place. To assign a group of points to a given molecule, we need to find the set of symmetric operations that exist on it. Symmetric operations are movements such as rotation around an axis or reflection through a mirror plane. In other words, it is the operation of moving molecules so that they cannot be distinguished from the original configuration. In group theory, the axis of rotation and the plane of the mirror are called "symmetric elements." These elements may be points, lines, or planes at which symmetric operations are performed. The symmetry of a molecule determines a particular group of points for this molecule.

There are five important symmetric operations. They are identity operations (E), rotation operations (C_n), reflection operations (σ), inversion (i), rotation reflection operations, or improper rotation (S_n). The identity operation (E) consists of leaving the molecule intact. This value is equal to the total number of rotations around the axis. This is the symmetry of all molecules, while the symmetry group of chiral molecules consists of only the equivalent action. The identity operation is a feature of all molecules, even without symmetry. Rotation around an axis consists of rotating a molecule at a specific angle around a specific axis. It rotates through an angle of 360 °/ n, where n is an integer with respect to the axis of rotation.

In reflection, many molecules have mirror planes. The reflection operation is exchanged left and right as if each point is moving in a vertical direction through a plane. When the plane is perpendicular to the main axis of rotation, it is called: σh (numerical). The other plane containing the main axis of rotation is labeled vertical (σv) or dihedral ( σd).

The reversal is a more complex task. Each point passes through the center of the molecule and moves to a position opposite to its original position, moving from the center point to the point from which it started. For example, methane and other tetrahedral molecules lack inversion symmetry. To see this, take a methane model with two hydrogen atoms on the right vertical plane and two hydrogen atoms on the left horizontal plane. Inversion produces two hydrogen atoms in the horizontal plane on the right and two hydrogen atoms in the vertical plane on the left. Therefore, since the direction of the molecule according to the inversion action is different from the original direction, the inversion action is not a symmetrical action of methane. And either the last operation is improper rotation or the rotation reflection operation requires a rotation of 360 °/ n, where n and then a reflection through a plane perpendicular to the rotation axis. A COMSOL Multiphysics simulator is used to investigate their characteristics.

Tin oxide (SnO₂) has space group number 136. First of all, atomic structure and its topview of SnO₂ are presented in Figure 1(a) and (b), respectively.

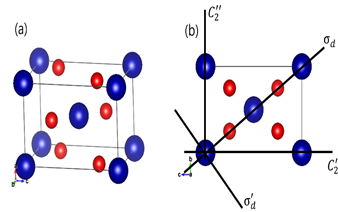
Figure 1 (a) atomic structure and (b) topview of SnO₂. Blue and red spheres are represent Sn and O atoms, respectively. (These figures are drawn by visualization program, VESTA).

If we choose one Sn atom which is placed at the corner as the original position, (0,0,0), the symmetry operations with τ =(0.5,0.5,0.5) are given as:

$\begin{array}{l}ϵ\left|0,C_2\right|0,C_4|\overrightarrow{\tau },C_4^3\left|\tau ,C_{2\text{'}}\right|\tau ,\hfill \\ C_2^{\text{''}}\left|\tau ,{\sigma }_d\right|0,{\sigma }_{d\text{'}}\left|0,i\right|0,i{C}_2\left|0,i{C}_4\right|\tau ,\hfill \\ C_4^3\left|0,i{C}_{2\text{'}}\right|\overrightarrow{\tau },i{C}_2^{\text{''}}\left|\tau ,i{\sigma }_d\right|0,i{\sigma }_{d\text{'}}|0\hfill \\ \hfill \end{array}$   (1)

In the international tables for X-ray crystallography, the sites of Sn and O location are 2a and 4 $f$ , respectively.

We find the equivalence transformation for SnO₂ at the center of the Brillouin zone (Table 1).

Also we find the lattice modes at the zone center $k=0$ , including their symmetries, degeneracies and the normal mode patterns.

At $k=0$ , the wave vector group contains the full symmetry operations of the space group. The character table of the group of the wave vector would be the same as that of $D_{4h}$  because of the phase factor $e^{iK\tau }=1$ . By using the charater table of $D_{4h}$ , we have χ(Sn)= A_1g+B _2g, χ(O)= $A_{1g}+B_{2g}+E_u$ , and = ${\chi }_{vector}=A_{1g}+E_u$ .

Therefore, the lattice vibration normal modes are given as equation (2).

$\begin{array}{l}\left[\chi \left(Sn\right)+\chi \left(O\right)\right]\otimes {\chi }_{vector}\hfill \\ =\left(2A_{1g}+2B_{2g}+E_u\right)\otimes \left(A_{2u}+E_u\right)\hfill \\ =A_{1g}+A_{2g}+2A_{2u}+B_{1g}+2B_{1u}+B_{2g}+E_g+4E_u\hfill \end{array}$   (2)

Since all the representations of D _4h are one dimensional except for E _μ and E _g, they have single modes without degeneracy while E _μ and E _g modes are doubly degenerated. A _2μ moves along z direction. Both Sn and O atoms are out-of-phase.

B _1μ also moves along z direction. Two Sn atoms which is placed different sites point opposite directions. Similar with Sn, two SnO atoms which is placed different sites point opposite directions. There are two kinds of E _g. And both move along z-direction. Movements of E_μ is similar with E_g . But they translate into x and y directions.

For a next step we indicate the IR-activity and Raman activity of these modes. IR-active modes includes A_2μ  and 3E_μ  while Raman acitvity modes represent A _1g, B_1g , B _2g and E_g .

#1 The A_2μ  mode is active to z-polarized light while 3E_μ  modes are active to x or y polarized light.

#2 A_1g  and B_1g  have diagonal matrix elements but B_2g  and E_g  are off-diagonal.

When we move away from k = 0 the mode splitting along the (100) and (001) directions, the group of the wave vector contains $\left\{ϵ\right|0\},\{i{C}_{2z}\left|0\right\},\left\{C_{2x}\right|\overrightarrow{\tau }\}$ , and $\left\{i{C}_{2y}\right|\overrightarrow{\tau }\}$ . Two dimensional k-space is presented in (Figure 2).

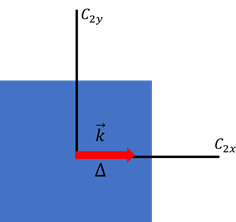
Figure 2 2-dimensional K-space. Direction of the mode splitting is denoted as an red arrow. (I remake this figure which is in dresselhaus lecture note).

The individual characters are given in Table 2, where the phase factor $e{}^{i\overrightarrow{K}\overrightarrow{\tau }}$ is taken out.

Now, we use the decomposition rule to see how the representations at Γ split in to Δ1, Δ2, Δ3, and Δ4 (Table 3).

Now, along (001) direction, the group of the wave vector contains $\left\{\Delta \epsilon \right|0\},\{C_4\left|\overrightarrow{\tau }\right\},\left\{C_4^3\right|\overrightarrow{\tau }\},\{C_{2z}\left|0\right\},\left\{i{C}_{2x}\right|\overrightarrow{\tau }\},\{i{C}_{2y}\left|\overrightarrow{\tau }\right\},\left\{{\sigma }_d\right|0\}$ , and $\left\{{\sigma }_{d\text{'}}\right|0\}$ .

Since the point symmetry operations form C  point group, the character can be given as Table 4, where the phase factor $e{}^{i\overrightarrow{K}\overrightarrow{\tau }}$  is taken out (as same as (100) case). 

Table 5 shows the decomposition of each mode.  

The splitting mode is presented in Figure 3.

Figure 3 Sketchy of the mode splitting behaviors.

Energy dispersion

Using the empty lattice, we find the energy eigenvalues, degeneracies and symmetry types for the two electronic levels of lowest energy for the fcc lattice at the Γ  point ( $\overrightarrow{k}$  = 0). Note that the lowest energy state is a non-degenerate state with ${\text{Γ }}_1^{+}$  symmetry.

Reciprocal lattice of fcc →  bcc lattice

The nearest neighbor point in reciprocal lattice:

$\begin{array}{l}\frac{2\pi }{a}\left(111\right),\frac{2\pi }{a}\left(-111\right),\frac{2\pi }{a}\left(1-11\right),\hfill \\ \frac{2\pi }{a}\left(11-1\right),\frac{2\pi }{a}\left(-1-11\right),\frac{2\pi }{a}\left(-11-1\right),\hfill \\ \frac{2\pi }{a}\left(1-1-1\right),\frac{2\pi }{a}\left(-1-1-1\right).\hfill \end{array}$   (3)

At Γ  point, the energy eigenvalues are given by

$E=\frac{{\hslash }^2}{2m}{\overrightarrow{\kappa }}^2$ , where ${\overrightarrow{\kappa }}^2$  is the reciprocal lattice vector. Therefore, the lowest energy eigenvalue = 0. Also, second lowest energy eigenvalue can be obtained as followed equation.

$\frac{{\hslash }^2}{2m}{(\frac{2\pi }{a})}^2\left(1^2+1^2+1^2\right)=6\frac{{\pi }^2{\hslash }^2}{m{a}^2}$   (4)

Since there are 8 equivalent {1 1 1} points, the degeneracy of the second lowest level is 8. The group of the wave vector at Γ  point is $Oh$ . The characters for the equivalent transform are shown in Table 6.

Therefore, lowest energy and second lowest levels are

${\chi }_{000}={\text{Γ}}_1^{+}\left(lowest\right)$   (5)

${\chi }_{111}={\text{Γ}}_1^{+}+{\text{Γ}}_2^{-}+{\text{Γ}}_{15}^{-}+{\text{Γ}}_{25}^{+}\left(second\right)$   (6)

We also find the appropriate linear combination of plane waves which provide basis functions for the two lowest L-point electronic states for the fcc lattice.

At L($\frac{\pi }{a},\frac{\pi }{a},\frac{\pi }{a}$ ) point, the energy levels are given by E= $\frac{{\hslash }^2}{2m}$  (k₁ + k). The lowest energy level corresponds to

$\kappa =\frac{2\pi }{a}$ =  (0,0,0) and $\kappa =\frac{-2\pi }{a}$ =  (-1,-1,-1) with E₀ = $\frac{3}{2}\frac{{\pi }^2{\hslash }^2}{m{a}^2}$

The plane waves are $e{}^{i\frac{\pi }{a}\left(x+y+z\right)}$ for (111) and $e{}^{-i\frac{\pi }{a}\left(x+y+z\right)}$ for (-1-1-1).

The second energy level consists of k= $\frac{2\pi }{a}$ (-1-11), $\frac{2\pi }{a}$ (1-1-1), $\frac{2\pi }{a}$ (-11-1), $\frac{2\pi }{a}$ (00-2), $\frac{2\pi }{a}$ (0-20), $\frac{2\pi }{a}$ (-200) with E₁ = $\frac{11}{2}\frac{{\pi }^2{\hslash }^2}{m{a}^2}$ .

The corresponding plane waves are:

$\begin{array}{l}{e}^{i\frac{\pi }{a}\left(-x-y+3z\right)},e^{i\frac{\pi }{a}\left(x+y-3z\right)},e^{i\frac{\pi }{a}\left(x-3y+z\right)},\hfill \\ e^{-i\frac{\pi }{a}\left(x-3y+z\right)},e^{i\frac{\pi }{a}\left(3x-y-z\right)},e^{-i\frac{\pi }{a}\left(3x-y-z\right)}.\hfill \end{array}$   (7)

We denote these plane wave states by (-1-13), (11-3), (1-31), (3-1-1), (-311).

At L point, the group of the wave vector is D_3d , the character is shown in Table 7.

The equivalence transform of the plane waves are shown in Table 8.

The symmetry of the lowest state at L point is L${}^{+}{}_1$  + L${}^{-}{}_2$ . The basis functions of the two symmetry states are:

$\begin{array}{l}{L}_1^{+}:\frac{1}{2}\left[\left(111\right)+\left(-1-1-1\right)\right]=cos\frac{\pi }{a}\left(x+y+z\right)\hfill \\ L_2^{-}:\frac{1}{2i}\left[\left(111\right)-\left(-1-1-1\right)\right]=sin\frac{\pi }{a}\left(x+y+z\right)\hfill \end{array}$   (8)

The symmetry of the second lowest state is $L{}^{+}{}_1+L{}^{+}{}_3+L{}^{-}{}_2+L{}^{-}{}_3$ . The basis functions are obtained as follows:

$\begin{array}{l}{L}_1^{+}:\left(-1-13\right)+\left(11-3\right)+\left(-13-1\right)+\left(1-31\right)+\left(3-1-1\right)+\left(-311\right)\\ =cos\frac{\pi }{a}\left(x+y-3z\right)+cos\frac{\pi }{a}\left(x-3y+z\right)+cos\frac{\pi }{a}\left(3x-y-z\right)\\ L_3^{+}:\left(-1-13\right)-\left(11-3\right)+\left(-13-1\right)-\left(1-31\right)+\left(3-1-1\right)-\left(-311\right)\\ =sin\frac{\pi }{a}\left(x+y-3z\right)+sin\frac{\pi }{a}\left(x-3y+z\right)+sin\frac{\pi }{a}\left(3x-y-z\right)\\ L_2^{-}:\left(-1-13\right)+\left(11-3\right)+\omega \left[\left(-13-1\right)+\left(1-31\right)\right]+{\omega }^2\left(3-1-1\right)+\left(-311\right)]\\ =cos\frac{\pi }{a}\left(x+y-3z\right)+\omega cos\frac{\pi }{a}+{\omega }^{2}cos\frac{\pi }{a}\left(3x-y-z\right)\\ L_3^{-}:\left(-1-13\right)-\left(11-3\right)+\omega \left[\left(-13-1\right)-\left(1-31\right)\right]+{\omega }^2\left(3-1-1\right)-\left(-311\right)]\\ =sin\frac{\pi }{a}\left(x+y-3z\right)+\omega sin\frac{\pi }{a}+{\omega }^{2}sin\frac{\pi }{a}\left(3x-y-z\right)\end{array}$   (9)

We had have question that "which states of the lower and upper energy levels in (a) and (b) are coupled by optical dipole transitions?".

At Γ points, $\chi {}_{vector}$ = ${\text{Γ }}_{15}^{-}$ . The lowest energy state has symmetry ${\text{Γ }}_1^{+}$ .

${\text{Γ}}_1^{+}\otimes {\text{Γ}}_{15}^{-}={\text{Γ}}_{15}^{-}.$   (10)

Therefore, only the ${\text{Γ}}_{15}^{-}$  state in the second energy level will couple with ${\text{Γ}}_1^{+}$  state in the lowest energy level. At L point, ${\chi }_{vector}=L{\text{'}}_2+L{\text{'}}_3$ . The lowest level has symmetry L₁ +L’₂ . For L₁  state, L₁   $\otimes$  (L’₂ +L’₃ )= L’₂ +L’₃. Therefore, the L₁  state in the lower level will couple with L’₂  and L’₃  states in the upper level via optical transition.

For L₂  state, L’₂   $\otimes$  (L’₂ +L’₃ )= L₁ +L₃ . Therefore, the L’₂  state in the lower level is coupled with L₁  and L₃  states (Figure 4).

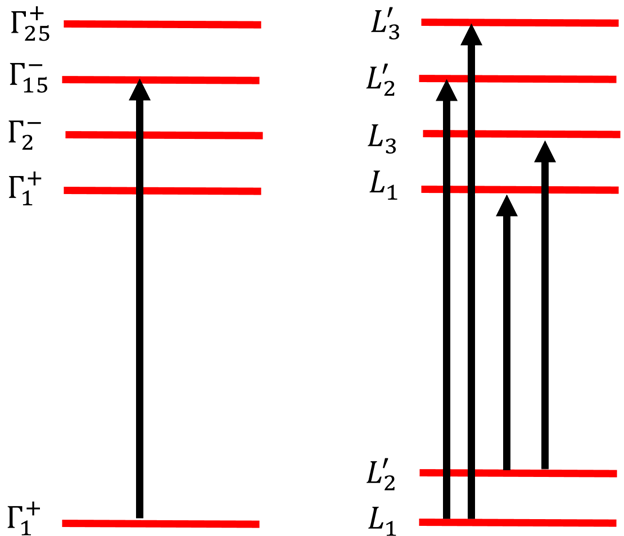
Figure 4 Sketchy of the transition behaviors.

Using compatibility relations, we find the symmetries of the energy levels that connect the two -point and two L-point energy levels. For  = ($\overrightarrow{k}=(\kappa ,\kappa ,\kappa )$ ), the group of wavevector is C_3v  {E,2C₃, 3 $\sigma {}_v$ }.

Therefore equations are presented as followed.

$\begin{array}{l}{\text{Γ}}_1^{+}\to {\wedge }_1\to L_1\hfill \\ {\text{Γ}}_2^{-}\to {\wedge }_1\to L{\text{'}}_2\hfill \\ {\text{Γ}}_{15}^{-}\to {\wedge }_1+{\wedge }_3\to L{\text{'}}_2+L{\text{'}}_3\hfill \\ {\text{Γ}}_{25}^{-}\to {\wedge }_1+{\wedge }_3\to L_1+L_3\hfill \\ \hfill \end{array}$   (11)

Perturbation theory

Using Ek perturbation theory and we find the form of the kp relations near the L-point in the Brillouin zone for a face centered cubic lattice arising from the lowest levels with L₁  and L’₂  symmetry that are doubly degenerate in the free electron model.

Let’s assume |i>  has L₁  symmetry and |j>  has L₂  has L’  symmetry. Since $\overrightarrow{p}$  transform as a vector,

${\chi }_{vector}$ =L’₂ +L’₃  at L point.

L₁  $\otimes$  L’₂  = L’₂ . So it contains L’₂ .

L₂   $\otimes$  L’₃₂  = L’₃ . So it does not contains L’₂ .

Now, let’s take the new ${\kappa }_1$ , ${\kappa }_2$ , and ${\kappa }_3$  coordinates where ${\widehat{\kappa }}_1$  is parallel to (111) in the original coordinate. In this new coordinate, ${\kappa }_1$  transforms like $L{\text{'}}_2$  whereas ${\kappa }_2$ , and ${\kappa }_3$  transform like $L{\text{'}}_3$ .

Therefore, the only non-vanishing matrix element is

$\langle i|p_1|j\rangle =\langle L_1|p_1|L{\text{'}}_2\rangle =\alpha$   (12)

Then, equation would becomes

$ϵ\left(\kappa \right)=\pm \frac{1}{2}{({ϵ}_g^2+\frac{4{\hslash }^2}{m^2}{\kappa }_1^2{\alpha }^2)}^{1/2}$   (13)

Therefore,

$E_n\left(\overrightarrow{k}\right)=\frac{{\hslash }^2{({\overrightarrow{k}}_0+\overrightarrow{\kappa })}^2}{2m}\pm \frac{1}{2}{({ϵ}_g^2+\frac{4{\hslash }^2}{m^2}{\kappa }_1^2{\alpha }^2)}^{1/2}$   (14)

Using the Slater Koster technique, we find the form for E(k) for the lowest two levels for a face centered cubic lattice.

For fcc lattice, d=0 is the zeroth neighbor at a(0,0,0), d=1 is the nearest neighbor at a(1/2,1/2,0) and d=2 are the second nearest neighbor at a(1,0,0).

$E_n\left(\overrightarrow{k}\right)={ϵ}_n\left(0\right)+{ϵ}_n\left(1\right)[cos\frac{a}{2}\left(k_y+k_z\right)+cos\frac{a}{2}\left(k_y-k_z\right)+cos\frac{a}{2}\left(k_z+k_x\right)+cos\frac{a}{2}\left(k_z-k_x\right)+cos\frac{a}{2}\left(k_x+k_y\right)+cos\frac{a}{2}\left(k_x-k_y\right)]+\mathrm{...}$   (15)

We expand your our results for the L-point in a Taylor expansion. At L point, ${\overrightarrow{k}}_0=\left(\frac{\pi }{a},\frac{\pi }{a},\frac{\pi }{a}\right)$

Let  $\overrightarrow{k}={\overrightarrow{k}}_0+\overrightarrow{\kappa }$

then

$cos\frac{a}{2}\left(k_y+k_z\right)=cos\frac{a}{2}\left(\frac{2\pi }{a}+{\kappa }_y+{\kappa }_z\right)=-1+\frac{1}{2}\frac{a^2}{4}{({\kappa }_y+{\kappa }_z)}^{2}cos\frac{a}{2}\left(k_y-k_z\right)=1-\frac{1}{2}\frac{a^2}{4}{({\kappa }_y-{\kappa }_z)}^{2}cos{k}_{x}a=cos\left(a\left(\frac{\pi }{a}+{\kappa }_x\right)\right)$   (16)

Therefore

$E_n\left(\overrightarrow{k}\right)=E_n\left({\overrightarrow{k}}_0+\overrightarrow{\kappa }\right)=ϵ{\text{'}}_n\left(0\right)+ϵ{\text{'}}_n\left(1\right){({\kappa }_x+{\kappa }_y+{\kappa }_z)}^2/2+\left(ϵ{\text{'}}_n\left(2\right)-ϵ{\text{'}}_n\left(1\right)/2\right)\left({\kappa }_x^2+{\kappa }_y^2+{\kappa }_z^2\right)$   (17)

 Now, let’s use ${\kappa }_1$ , ${\kappa }_2$ , ${\kappa }_3$   coordinate where ${\kappa }_1$  is parallel to (111) direction.

Then we obtain followed equation.

$E_n\left({\overrightarrow{k}}_0+\overrightarrow{\kappa }\right)={ϵ}_n^{\text{''}}\left(0\right)+{ϵ}_n^{\text{''}}\left(1\right){\kappa }_1^2+{ϵ}_n^{\text{''}}\left(2\right){\kappa }^2=\alpha +\beta {\kappa }_1^2+\gamma \left({\kappa }_2^2+{\kappa }_3^2\right)$   (18)

Now, let’s Taylor expand the result.

$E_n\left(\overrightarrow{k}\right)=\frac{{\hslash }^2}{2m}(|{\overrightarrow{k}}_0{|}^2+2\left|{\overrightarrow{k}}_0\right|{\kappa }^2)\pm \frac{1}{2}{({ϵ}_g^2+\frac{4{\hslash }^2}{m^2}{\alpha }^2{\kappa }_1^2)}^{1/2}=\alpha \text{'}+\beta \text{'}{({\kappa }_1+\delta )}^2\gamma \text{'}\left({\kappa }_2^2+{\kappa }_{{}^2}\right)$   (19)

This result suggests that carriers at L point have anisotropic effective mass tensor.

Application of perturbation theory

Using perturbation theory, we find the form of the secular equation for the valence band of Si with ${\text{Γ}}_{25}^{+}$  symmetry. For the valence band of Si with ${\text{Γ}}_{25}^{+}$  symmetry, we use the degenerate $kp$  perturbation theory. Due to the parity requirement ($\langle {\text{Γ}}_{25}^{+}\left|H\text{'}\right|{\text{Γ}}_{25}^{+}\rangle$ =0 since H’ has the odd parity), we have to to the second-order perturbation.

Since H’ transforms like ${\text{Γ}}_{15}^{-}$  and ${\text{Γ}}_{25}^{+}$   $\otimes$   ${\text{Γ}}_{15}^{-}$  = ${\text{Γ}}_2^{-}$  +${\text{Γ}}_{12}^{-}$  +${\text{Γ}}_{15}^{-}$  +${\text{Γ}}_{25}^{-}$ ,

${\text{Γ}}_{25}^{+}$  is coupled with only the following intermediated states;

${\text{Γ}}_2^{-},{\text{Γ}}_{12}^{-},{\text{Γ}}_{15}^{-},{\text{Γ}}_{25}^{-}$    (20)

For $\overrightarrow{k}=\left(\kappa ,\kappa ,\kappa \right)$  where $0<\kappa <\frac{\pi }{a}$ , the secular equation becomes followed equation.

$E=E^0+\frac{L+2M\pm 2N}{3}{\kappa }^2$   (21)

 If we suppose that our silicon sample is a thin film with 10 nm thick grown pseudomorphically on a germanium substrate, what happens to E(k) for the silicon valence band in the thin film if the germanium substrate is oriented along a (100) direction or if it is oriented along a (110) direction? Since there is a lattice mismatch between Si and Ge, thin silicon film has tensile stress when it grows on Ge substrate. Therefore, the symmetry of the crystal is reduced as follows:

$\begin{array}{l}\left(100\right)\text{direction}Oh\to D_{4h}\hfill \\ \left(110\right)\text{direction}Oh\to D_{2h}\hfill \end{array}$   (22)

Nature of SnO₂ particles strongly influenced the corresponding Raman spectra. According to our study using group theory, a single SnO₂ crystal with rutile-type structure shows four Raman active modes, A _1g, B _1g, B _2g and E _g. The additional A _2μ and E _μ modes correspond to transverse-optical (TO) and longitudinal-optical (LO) vibrations. Moreover, we applied application of perturbation theory, consequently, the spectrum of commercial SnO₂ sample showed the Raman bands in accordance with the theory.

The authors declare no conflict of interest with respect to the publication of this manuscript.

None.

None.

1. Yoichi Ogo, Hidenori Hiramatsu, Kenji Nomura, et al.  p-channel thin-film transistor using p-type oxide semiconductor, sno.   Applied Physics Letters. 2008;93(3).
2. Shujiang Ding, Deyan Luan, Freddy Yin, et al.  Sno2 nanosheets grown on graphene sheets with enhanced lithium storage properties.   Chemical Communications. 2011;47(25):7155–7157.
3. Spencer JA, Mock AL, Jacobs AG, et al.  A review of band structure and material properties of transparent conducting and semiconducting oxides: Ga2o3, al2o3, in2o3, zno, sno2, cdo, nio, cuo, and sc2o3.   Applied Physics Reviews. 2022;9(1).
4. Shumin Huang, Peiyu Li, Jing Wang, et al.  Modification of sno2 electron transport layer: brilliant strategies to make perovskite solar cells stronger.   Chemical Engineering Journal. 2022;439.
5. Pfeiffer CA, Economou EN, Ngai KL. Surface polaritons in a circularly cylindrical interface: surface plasmons.   Physical review B. 1974;10(8):3038.
6. Juan Alejandro Herbsommer, Gerd Schuppener, Robert Floyd Payne.  Dielectric waveguide with non-planar interface surface and mating deformable material. 2016.
7. Morcrette M, Chabre Y, Vaughan G, et al.  In situ x-ray diffraction techniques as a powerful tool to study battery electrode materials. Electrochimica Acta. 2002;47(19):3137–3149.
8. Alain Lafond, Léo Choubrac, Catherine Guillot-Deudon, et al.  X-ray resonant single-crystal diffraction technique, a powerful tool to investigate the kesterite structure of the photovoltaic cu2znsns4 compound.   Acta Crystallographica Section B: Structural Science, Crystal Engineering and Materials. 2014;70(2):390–394.
9. Tamura N, Celestre RS, MacDowell AA, et al.  Submicron x-ray diffraction and its applications to problems in materials and environmental science.   Review of scientific instruments. 2002;73(3):1369–1372.
10. Wangwei Ren, Jingkai Yang, Jiaxin Zhang, et al.  Recent progress in sno2/g-c3n4 heterojunction photocatalysts: synthesis, modification, and application.   Journal of Alloys and Compounds. 2022;906.
11. Zhicheng Cai, Sunghoon Park.  A superior sensor consisting of porous, pd nanoparticle–decorated sno2 nanotubes for the detection of ppb-level hydrogen gas.   Journal of Alloys and Compounds. 2022;907.
12. William Raymond Scott. Group theory. Courier Corporation. 2012.
13. Wu-Ki Tung. Group theory in physics. 1985;1.