In this paper a sandwich composite beam under three point bending. In the core material of the beam an initially small crack is considered. In this study a computational analysis is developed based on the extension of Elastic Fracture Mechanics to the Elasto-plastic Fracture Mechanics. The plastic zone length and the distribution of the stress field around the crack tip are evaluated. Furthermore an analysis of the cracking propagation path utilizing concepts of the Elastoplastic Fracture Mechanics Theory is performed. A finite element analysis code has been developed in order to predict the position of the direction and the length of the plastic zone ahead of the crack tip.

Keywords: composite structure, computational analysis, fiber reinforced plastics, fracture mechanics, von mises and tresca yielding criteria, stress intensity factors

The fracture behavior in sandwich composite structures has been directed toward the understanding of crack propagation, and at the same time toward improving the durability of composites against fracture ^[1-4]. A crack flaw may be introduced during processing or subsequent service conditions. It may result from low velocity impact, from eccentricities in the structural load path, or from discontinuities in structures, which induce a significant out-of-plane stress. Generally for a state of plane stress the stresses normal to the plane of interest are negligibly small. On the other hand plane strain is assumed to occur where the strains to the normal plane are negligibly small. In our study both these cases will be studied. The sandwich beam considered is shown in Figure 1. Material properties and geometrical data are shown in Tables 1 & Tables 2 respectively. Additional information regarding material properties as shear and tensile strength, are given in Table 3. In this study combining the elastoplastic concepts approach with the step by step crack propagation inside the core of a sandwich beam very close to the upper skin interface, a numerical solution is proposed via the finite element analysis.^1‒4 An initial crack length is assumed. Methods of evaluating the plastic zone under mixed mode loading conditions and small scale yielding ARE presented. In the presence of plastic zone at the crack tip the stiffness of the component decreases and the compliance increases. To incorporate the effect of plasticity in Fracture analysis the crack is mathematically modeled to be longer than the actual length. In the finite element model this is incorporated by taking into account the radius of singular elements around the crack tip. This radius is at the same order of magnitude with the crack tip plastic zone confronted in our analysis. The relations which relate the fracture parameters and the radius of the plastic as well as the direction of the propagation zone under the three point bending are presented. The extension of the plastic zone along the crack axis is succeeded by finding the point at which one of the yield criteria is satisfied. It is quite difficult to give a proper description of plastic zone shape and size. In all the models to simplify the analysis the material is assumed to be elastic-perfectly plastic. In this study considering that the plastic zones are created around the tips of the cracks under small scale yielding, the stress fields are determined in terms of the stress intensity factors using the asymptotic solutions.

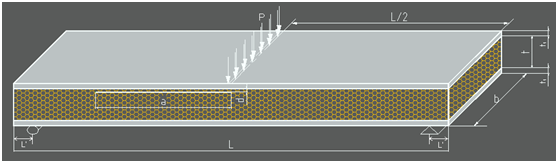
Figure 1 The model of the fractured sandwich beam and the applied loading.

At first our intention is to compare the plastic zone size in plane stress and plane strain conditions inside the core material of the sandwich beam. The stress field (Mode-I) close to the crack tip is given in terms of stress intensity factors at the polar coordinate system (r, θ) by: ^4‒8

$\left(\begin{array}{l}{\sigma }_x\hfill \\ {\sigma }_y\hfill \\ {\tau }_{xy}\hfill \end{array}\right)=\frac{K_I}{\sqrt{\text{2πr}}}\text{cos}(\theta /\text{2})\left\{\begin{array}{l}\text{1}-\text{sin}(\theta /\text{2})\text{sin}(\text{3}\theta /\text{2})\hfill \\ \text{1}+\text{sin}(\theta /\text{2})\text{sin}(\text{3}\theta /\text{2})\hfill \\ \text{sin}(\theta /\text{2})\text{cos}(\text{3}\theta /\text{2})\hfill \end{array}\right\}$    (1)

The corresponding principal stresses (Mode-I) are given as:

$\begin{array}{c}{\sigma }_{{\rm I}}\\ {\sigma }_{{\rm I}{\rm I}}\\ {\sigma }_{{\rm I}{\rm I}{\rm I}}\end{array}\}=\frac{{{\rm K}}_{{\rm I}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}\{\begin{array}{c}1+\sin \frac{\theta }{2}\\ 1-\sin \frac{\theta }{2}\\ 0\begin{array}{cc}for& planestress\end{array}\\ 2\nu \cos \frac{\theta }{2}\begin{array}{cc}for& planestrain\end{array}\end{array}$    (2)

The following Yield criteria will be used in our study:^5‒8

Von Mises Criterion:

${({\sigma }_I-{\sigma }_{II})}^{\text{2}}+{({\sigma }_{II}-{\sigma }_{III})}^{\text{2}}+{({\sigma }_{III}-{\sigma }_I)}^{\text{2}}\ge \text{2}{\sigma }_{{}_{ys}}^{\text{2}}$    (3)

Where the yield strength in uniaxial tension.

Tresca Criterion:

$\frac{{({\sigma }_I-{\sigma }_{II})}^{\text{2}}}{\text{2}}\ge \frac{{\sigma }_{ys}}{\text{2}}$    (4)

 Where  is the yield stress in pure shearing.

Substituting_, σ_I and σ_II from (2) in the above equations, the plastic zone size is obtained. The plastic zone length using Mises yield criterion is given by:^7,8,11

For plane strain (θ=0, v=1/3):

$r_p=\frac{\text{1}}{\text{18}\pi }{(\frac{K_I}{{\sigma }_{ys}})}^{\text{2}}$    (5)

For plane stress (θ=0,ν=1/3):

$r_p=\frac{\text{1}}{2\pi }{(\frac{K_I}{{\sigma }_{ys}})}^{\text{2}}$    (6)

The plastic zones magnitude (r_p1,r_p2) for plane strain and plane stress conditions according to relations (5) and (6) respectively are plotted in Figure 2. It can also be shown the variation of the σ_yy along the crack axis (x) and ahead of the crack tip. It is observed from Figure 2 that the plastic zone length (r_p1) for plane strain is lower than that the plastic zone length in plane stress (r_p2). Taking the Poisson ratio as ν=1/3 and using the Tresca yield criterion the maximum yield stress in plane strain is three times higher than the maximum yield stress in plane stress conditions.

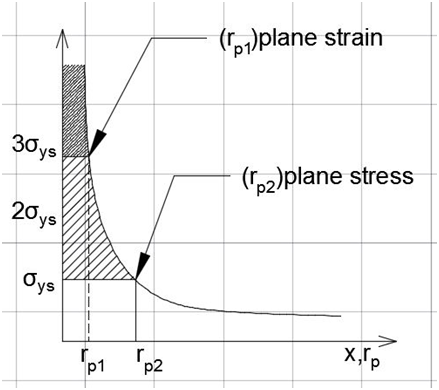
Figure 2 The plastic zone length¹¹ under plane stress and plane strain conditions.

The plastic zone shape

In this part of our study the shape of the plastic zone will be determined from a polar plot. We can find  for the same. It is useful to compare relatively the plastic zones for plane stress and plane strain conditions. This gives the first order approximation of the shape. The relationships involving the angle theta (θ) of the polar coordinate system (r,θ) at the crack tip and the plastic zone length for Mode-I and Mode -II conditions are:^7,8,11

For Mode-I plane stress:

$r_P=\frac{\text{1}}{\text{4π}}{\left(\frac{{{\rm K}}_{{\rm I}}}{{\sigma }_{ys}}\right)}^{\text{2}}\left(\text{1}+\frac{\text{3}}{\text{2}}{\text{sin}}^{\text{2}}\theta +\text{cos}\theta \right)\begin{array}{ll}for\hfill & VonMises\hfill \end{array}$    (7)

$r_P=\frac{\text{1}}{\text{2}\pi }{\left(\frac{{{\rm K}}_{{\rm I}}}{{\sigma }_{ys}}\right)}^{\text{2}}{\left(\text{cos}\frac{\theta }{\text{2}}\ast \left(\text{1}+\text{sin}\frac{\theta }{\text{2}}\right)\right)}^{\text{2}}\begin{array}{ll}for\hfill & Tresca\hfill \end{array}$    (8)

For Mode I plane strain:

$r_P=\frac{\text{1}}{\text{4}\pi }{\left(\frac{{{\rm K}}_{{\rm I}}}{{\sigma }_{ys}}\right)}^{\text{2}}\left(\frac{\text{3}}{\text{2}}{\text{sin}}^{\text{2}}\theta +{(\text{1}-\text{2ν})}^{\text{2}}\left(\text{1}+\text{cos}\theta \right)\right)\begin{array}{ll}for\hfill & VonMises\hfill \end{array}$    (9)

$r_P=\frac{\text{1}}{\text{2}\pi }{\left(\frac{{{\rm K}}_{{\rm I}}}{{\sigma }_{ys}}\right)}^{\text{2}}{\left(\text{cos}\frac{\theta }{\text{2}}\ast \left(\text{1}+\text{sin}\frac{\theta }{\text{2}}\right)\right)}^{\text{2}}\begin{array}{ll}for\hfill & Tresca\hfill \end{array}$    (10)

For Mode II plane stress:

$r_P=\frac{\text{1}}{\text{8}\pi }{\left(\frac{{{\rm K}}_{II}}{{\sigma }_{ys}}\right)}^{\text{2}}\left(14-9{\sin }^2\theta -2\cos \theta \right)\begin{array}{ll}for\hfill & VonMises\hfill \end{array}$    (11)

For Mode II plane strain:

$r_P=\frac{\text{1}}{\text{8}\pi }{\left(\frac{{{\rm K}}_{II}}{{\sigma }_{ys}}\right)}^{\text{2}}\left(12+2(1-\cos \theta ){(1-2\nu )}^2-9{\sin }^2\theta \right)\begin{array}{ll}for\hfill & VonMises\hfill \end{array}$    (12)

The shape of the plastic zone for plane strain and plane stress conditions and the considered yield criteria are shown at the following polar plots. The stress intensity factors Κ_a (a=I, II) for the relationships (7-12) in the general case of the infinite body with a crack may be obtained from Figure 3 & Figure 4 & Figure 5:

Figure 3 Polar plot for Mode-I, Tresca yield criterion.

Figure 4 Polar plot for Mode-I, Von Mises yield criterion.

Figure 5 Polar plot for Mode-II, Von Mises yield criterion.

$K_{II}={\tau }_{yy}\sqrt{\pi a}$    (13)

for Mode I where σ_yy is the remotely applied normal stress (Figure 6B) and:

$K_{II}={\tau }_{yy}\sqrt{\pi a}$    (14)

for Mode II where τ_xy is the remotely applied shear stress Figure 6A.

First a finite element model is introduced Figure 6. Contact analysis is assumed at the neighbor of the applied load and the supports. The ultimate load is kept constant during all steps of analyses. An initial crack with length 2mm is considered under the central load introduction and close to the upper skin interface. This crack is considering propagate under the interface to the left in accordance with the experimental verification.⁹ Furthermore between the upper and lower crack flanks we introduce contact elements and a self-contact nonlinear analysis in order to prevent the interpenetration between the crack lips. This model was solved in Abaqus.⁹ A number of twelve models have been solved. From every run we retrieve the stress intensity factors (K_I,K_II), the stress tensor at the crack tip and the principal stresses, the principal planes and the planes of maximum shear stress. Finally it is calculated the direction where the plastic deformation will take place. Then another model is built with a new crack length (the plastic zone length, relations (7)-(12)) and the direction of the angle “theta”. This occurs several times for a number of twelve models (Figure 7). The interaction between the Mode I and Mode II situation dictates the way which the crack propagates for a value of. That means that we proceed either along the principal plane or the maximum shear stress plane. The magnitude of the angle “theta” for the determination of the principal plane according to solid mechanics, is given by:^7,8

Figure 6 Remotely applied stresses for mode II (a) and mode I (b).

Figure 7 The finite element model.

$\text{tan2}{\theta }_p=\frac{\text{2}{\tau }_{xy}}{{\sigma }_x-{\sigma }_y}$    (8)

We add to the value of derived from (8) “forty five degrees” if the Mode II dominates. Then for this value of “theta”, is estimated from relations (7)-(12) (Figure 8).

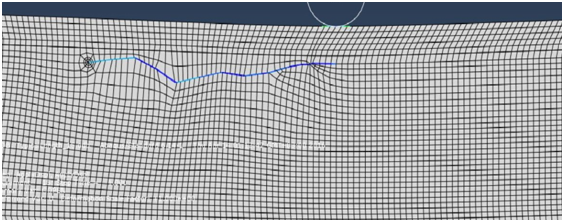
Figure 8 The crack propagation after twelve runs.

The stress intensity factors K_i and K_ii for opening and sliding modes respectively can be computed directly from the nodal displacements on opposite sides of the crack lips by^:10

$\begin{array}{c}{K}_I\\ K_{II}\end{array}\}=G\sqrt{\frac{2\pi }{r_0}}\{\begin{array}{c}\frac{u_y(r_0,\theta =\pi )-u_y(r_0,\theta =-\pi )}{(k+1)}\\ \frac{u_x(r_0,\theta =\pi )-u_x(r_0,\theta =-\pi )}{(k+1)}\end{array}$    (9)

where k=3-ν/(1+ν) ,k=3-4ν for plane stress and plane strain respectively and G is the shear modulus

The values of K_I and K_II versus the crack length are shown in Figure 9 under plane stain conditions. It is observed that as the crack length increases the values of become greater comparing from those of. The variation of the principal planes direction and the maximum shear stress planes direction are shown in Figure 10. It is observed that as crack length increases the “-maximum shear stress” increases. Finally the variation of the radius of the plastic zone for principal stress plane or maximum shear plane, are shown in Figure 11 for different crack lengths. It is observed that as the crack length increases the -maximum shear stress dominates. From Figure 9 & Figure 10 & Figure 11 it is observed a peak value at a crack length about 15mm.This is due to the fact either that K_II mode begins to dominate on K_I or it may be a numerical fault due to the tolerances of the solver regarding the interpenetration allowance among the contact elements.

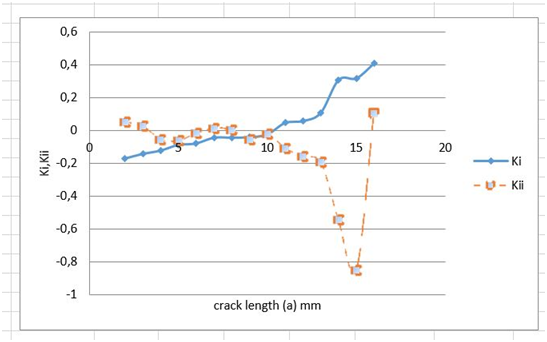
Figure 9 The Stress Intensity Factors versus the crack length.

Figure 8 The angle of principal stress planes and the maximum shear stress planes versus the crack length.

Figure 11 The variation of the plastic zone magnitude.

In this paper the crack propagation of a crack inside the core material of a sandwich beam very close to the upper skin was investigated under small scale yielding conditions. In order to predict the crack propagation in plane stress or plane strain conditions a quasi static loading was considered. At first the $$K_I,K_{II}$$ stress intensity factors were calculated via the Finite Element Method using the linear fracture mechanics approach. Due to the high nonlinear problem since the stress field under consideration lays at the compression zone of the specimen, a self-contact analysis was taken in order to succeed the solution of the problem. From the finite element analyses the principal planes and the planes of maximum shear stress were also calculated for every crack length and consequently the direction where the plastic deformation would appear. In the sequel, The Mises and Tresca yield criteria, were used in order to calculate the plastic zone length. Having determined the direction another crack length was considered in order to proceed with the crack propagation inside the core. The crack-tip plastic zones derived from Mises and Tresca yield criteria were about the same. The plastic zones predicted in plane stress conditions were greater than those in plane strain conditions.

Author declares that there is no conflicts of interest.

1. Carlsson, LA, Sendlein LS, Merry SL. Characterization of Face Sheet/Core Shear Fracture of Composite Sandwich Beams. Journal of Composite Materials. 1989;25:101‒116.
2. Kulkarni N, Mahfuz H, Jeelani S, et al. Fatigue crack growth and life prediction of foam core sandwich composites under flexural loading. Composite Structures. 2003;59:499‒505.
3. Berggreen C, Simonsen BC, Borum KK. Prediction of debond propagation in sandwich beams under FE-bared Fracture Mechanics and NDI Techniques. Journal of Composite Materials. 2007;41:493‒520.
4. Theotokoglou EE, Hortis D, Carlsson LA, et al. Numerical study of fractured sandwich composites under flexural loading. Journal of Sandwich Structures and Materials. 2008;10:75‒94.
5. Sih GC. Strain energy density factor applied to mixed mode crack problems. Int Journal Fracture Mech. 1974;10:305‒321.
6. Erdogan F, Sih GC. On the extension in plates under plane loading and transverse shear. Journal Basic Eng. 1963;85:519‒527.
7. Gdoutos EE. Fracture Mechanics an Introduction. Kluwer Academic Publishers: 1993.
8. Anderson TL. Fracture Mechanics, Fundamentals and Applications. Boca Raton; CRC Taylor & Francis: 2005.
9. Hibbit Karlsson, Sorensen. Abaqus/Standard and Abaqus/Explicit version 5.8. Pawtucket, USA: 1999.
10. Erdogan Madernci, Ibrahim Guven. The Finite Element Method And Applications in Engineering Using Ansys. Springer.
11. Ramesh K. Engineering Fracture Mechanics. ISBN 978-81-904235-0-2.