Auxetic materials and structures are a novel class of materials which have negative Poisson’s ratio. They have improved mechanical properties such as fracture toughness, indentation resistance, etc. They have several potential applications in medical, sports, automobile, defense, etc. Design and modeling of auxetic materials is still in progress. In this article we briefly introduce these materials and their different features and properties.

Keywords: auxetic materials, poisson’s ratio, mechanical properties

Auxetic materials are those which show counter-intuitive reaction to the applied force meaning, in contrast to the materials which thin transversely under axial tensile force, these materials thicken. Poisson’s ratio is a measure of the transverse strain relative to longitudinal strain Fung et al.¹ Claimed that the Poisson’s ratio is bounded between -1 and 0.5 for a linear elastic isotropic material. Cork is the material with zero Poisson’s ratio. It was shown in the work of Ting & Chen² that for anisotropic materials, Poisson’s ratio can be positive and negative on the condition that the strain energy density function is positive and definite. Then the negative Poisson’s ratio can be achieved in the man-made materials. Unlike the conventional materials Auxetic materials get shorter in transverse direction when they compressed in the longitude direction and vice versa. Auxetic materials have different potential applications in different fields such as medical, sports, automobile, etc. Lakes³ in 1987 was the pioneer work in the field of negative Poisson’s ratio materials which was fabricated first time foams with negative Poisson’ ratio. Evans⁴ termed the “Auxetics” from Greek word “auxetos” which means “that may be increased”. In this article we briefly introduce these materials, some mechanical properties of them and their different modes. Figure 1 compares the conventional and auxetic materials during loading in Y direction.

Figure 1 Loading in the Y-direction of a conventional and auxetic honeycomb structure.

Here in this part we present first Eigen modes of 2D structures with periodic boundary conditions. Taking into account the periodic boundary conditions, Figure 2 shows the first Eigen modes of the hexagonal, quadratic as well as triangular 2D basic cell. There is a direct relationship between the number of nodes and number modes. The number of modes increases with the number of nodes in the basic element. In particular, the number of nodes for the triangular, quadratic and hexagonal basic elements is 3, 4 and 6 respectively which explains the dependence of the number of modes on the unit cell types noted in the Figure 2. For each lattice cell, these Eigen modes were assembled to form a periodic lattice structure. Numerical testing performed by applying a negative strain in the x-y direction.⁵

Figure 2 Loading in the Y-direction of a conventional and auxetic honeycomb structure [5].

Applications of auxetics

Medical and biomedical application: Bhullar et al.,^6,7 Ali et al.⁸ used Auxetic materials in stents. By means of the laser cutting machine the structure was manufactured. The structure of squares with holes⁸ was lighter in weight and reduces obstruction and food impaction. Manufacturing of oesophageal stents with drug carrying system⁷ was carried out utilizing the auxetic properties of rotating squares mechanism.

Sports applications: The Auxetic materials are used in protective devices such as pads, gloves, helmets, and mats which can provide better comfort and support for athletes and also can enhance energy absorption while being light.

Fashion application: Auxetic yarns and textiles^9,10 are being used for different applications in fabrics, garments, and fashion apparels. A fabrication of 3D Auxetic fabric¹¹ was carried out based on parallelogram geometry and a better shape flexibility ability of Auxetic fabrics was found.

The Poisson’s ratio and Young’s modulus in the Basic form of Auxetic Materials (Re-entrant type)

Figure 3 shows the geometry of 2D re-entrant structure as analyzed by Smith et al.¹² according to Smith et al.,¹² the Poisson’s ratio and Young’s modulus in the direction of loading are given as follows:

${\nu }_{12}=\frac{\sin \theta (h/l+\sin \theta )}{{\cos }^2\theta }$

$E_1=k\frac{(h/l)+\sin \theta }{b{\cos }^3\theta }$

Where h denotes the half of the length of horizontal strut, l denotes the length of inclined strut, and b is the depth of strut into the plane of paper. The parameter k can be evaluated from Equation (3).

$k=E_{s}b{(\frac{t}{l})}^3$

Where $E_s$ the Young’s modulus of base material of cell and t is is the thickness of the strut.

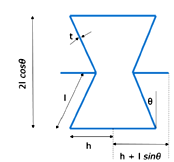
Figure 3 Geometrical representation of 2D re-entrant structure.¹²

There exist a number of methods to enhance mechanical properties of the materials and render those fabulous capabilities such as reducing grain size or introducing reinforcing phase in metals¹³ and producing polymer composites,¹⁴ etc. Auxetic composites are counted among structures owing interesting properties thanks to their auxetic nature. These composites possess the properties of other composites, plus some unique properties of their own like higher shear modulus, higher damping resistance and synclastic curvature. Main manufacturing methods of such composites are by using the laminated angle-ply method and by using auxetic inclusions with different geometry.¹⁵ The primary step in composite manufacturing using laminated angle-ply method is to design the sequence of the plies which can give a auxetic property to the final manufactured composite. In the other method of Auxetic manufacturing method, shapes with auxetic behaviour are incorporated into the composite to be manufactured. One important thing about the auxetic shapes used in the composite is that, their poisson's ratio is positive and it is the auxetic design of the shapes that gives composite auxetic behaviour.¹⁵

Yunan Pravoto¹⁶ in a paper published the results of the study. Although the study is based on the ordered microstructure, the author states that, the future researches will be focused on the disordered microstructures. Victor Salit¹⁷ studied the feasibility of inducing auxetic behaviour in the thin walled structures. The results of this study show, by out-of-plane corrugations, it is possible to induce auxetic behaviour in the thin walled structures. In a research conducted by Gaoyuan Wei et al.¹⁸ in which auxetic material was embedded in the elastic material, it is theoretically shown that, the resultant composite material exhibits auxetic behaviour. It is also claimed that, providing that it is verified experimentally, a new era in the research on the field of auxetic material will begin. In another research done by Igor.¹⁹ It is demonstrated that, by creating hybrid structure from auxetic and non-auxetic phases, it is possible to obtain considerable increase in stiffness which surpasses the stiffness’s of the phases. A research²⁰ on the effect of negative Poisson’s ratio on the hardness of ultra high molecular weight polyethylene done by K. L. Alderson showed a increase of hardness by a factor of two. In another research, Lili Jiang et al.²¹ by using multilayer orthogonal auxetic structure as reinforcement and polyurethane foam as matrix via an injecting and foaming process a novel kind of auxetic composite was fabricated and the obtained results show, fabricated auxetic composite behaves more like a damping material with a large range of deformation strain. A AIderson et al.,²² showed in their study, because of their unique pore-opening properties, auxetic materials offer improved filter performance from the macro-scale to the nano-scale.

Auxetics with their outstanding capability of expansion and contraction every which way, under tension and compression respectively, are potentials in many engineering application like shock and vibration absorbers, easy-to-clean filters and so on. Also in biomedical field, these materials can be top candidates to be considered like in making heart vessel dilating devices, which expand under tensile force and widens the obstructed area in the blood vessel. Although many engineering obstacles remain to be solved by materials with negative Poisson’s ratio, this cannot happen before the suggested uses of these materials come to fruition commercially.

None.

The author declares no conflict of interest.

1. Fung YC. Foundations of Solid Mechanics. USA: Prentice–Hall; 1965.
2. Ting TCT, Chen T. Poisson’s ratio for anisotropic elastic materials can have no bounds. Q J Mech Appl Math. 2005;58(1):73.
3. Lakes R. Foam Structures with a Negative Poisson's Ratio. Science. 1987;235:1038.
4. Evans KE. Auxetic polymers: a new range of materials. Endeavour. 1991;15:170.
5. Körner C, Liebold–Ribeiro Y. A systematic approach to identify cellular auxetic materials. Smart Materials and Structures. 2014;24(2):025013.
6. Bhullar SK, Mawanane Hewage AT, Alderson A, et al. Adv Mater. 2013;2:42.
7. Bhullar SKK, Ahmed F, Ko J, et al. Using mathematical modeling to control topographical properties of poly (ε–caprolactone) melt electrospun scaffolds. Int J Mech Aerosp Ind Mechatron Manuf Eng. 2014;24(6):446.
8. Ali M, Busfield JC, Rehman I. Auxetic oesophageal stents: structure and mechanical properties. Journal of Materials Science: Materials in Medicine. 2014;25(2):527.
9. Sloan MR, Wright JR, Evans KE. The helical auxetic yarn–a novel structure for composites and textiles; geometry, manufacture and mechanical properties. Mech Mater. 2011;43:476.
10. Miller W, Ren Z, Smith CW, et al. A negative Poisson's ratio carbon fibre composite using a negative Poisson's ratio yarn reinforcement. Composites Science and Technology. 2012;72(7):761.
11. Wang Z, Hu H. Auxetic wrap–knitted spacer fabrics. Physica Status Solidi. 2014;251(2):281.
12. Smith CW, Grima JN, Evans KE. A novel mechanism for generating auxetic behavior in reticulated foams: missing rib foam model. Acta materialia. 2000;48(17):4349.
13. Ashjari M, MostafapourAsl A, Rouhi S. Experimental investigation on the effect of process environment on the mechanical properties of AA5083/Al2O3 nanocomposite fabricated via friction stir processing. Mat Sci & Eng A. 2015;645:40–46.
14. Ehsan Azarsa, Amir Mostafapour Asl. On the feasibility of producing polymer–metal composites via novel variant of friction stir processing. J Manuf Process. 2013;15:682–688.
15. Sohel Rana, Raul Fangueiro. Advanced Composite Materials for Aerospace Engineering. 2016;1:213–240.
16. Yunan Prawoto. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Computational Materials Science. 2012;58:140–153.
17. Victor Salit, Tanchum. Weller, On the feasibility of introducing auxetic behavior into thin–walled structures. Acta Materialia. 2009;57:125–135.
18. Gaoyuan Wei, Edwards SF. Auxeticity windows for composites. Physica A. 1998;258:5–10.
19. Igor Shufrin, Elena Pasternak, Arcady V Dyskin. Hybrid materials with negative Poisson’s ratio inclusions. International Journal of Engineering Science. 2015;89:100–120.
20. Alderson KL, Pickles AP, Neale PJ, et al. Auxetic Polyethylene: The Effect of a Negative Poisson's Ratio on Hardness. Acta Metallurgica et Materialia. 1994;42:2261–2266.
21. Lili Jiang, Bohong Gu, Hong Hu. Auxetic composite made with multilayer orthogonal structural reinforcement. Compos Struct. 2015;135:23–29.
22. AIderson A, Rasburn J, Evans KE, et al. Auxetic, polymeric filters display enhanced de–fouling and pressure compensation properties. Membrane Technology. 2001;137:6–8.