A non-autonomous ordinary differential equations model was developed from the theoretical model of a nonlinear network previously developed by us. The proposed network-modified model qualitatively shows that mole-rates, when subjected to hostile conditions such as variations of the oxygen of the environment, maintain high robustness to environmental changes, which ensures its adaptability to the surroundings.

Keywords: mole-rats, aging, longevity, complexity

Longevity and aging are one of the most important current challenges for science and remain one of the most fascinating and intriguing topics of human knowledge. Despite all the achievements in biomedical sciences,^1–3 the underlying mechanisms of senescence remain a mystery and a challenge for the scientific community. In nature, there are exceptions where longevity and aging do not follow normal dogmas of behavior⁴. Particular and fascinating organisms, such as mole-rats, represent an ideal model to analyze the aging process⁵ due to the non-linear network of interactions that form the overexpressed high molecular mass hyaluronic acid, especially in your skin.^6,7

Within the rodent family a paradigmatic species has appeared, the mole-rats, which exhibit a longevity that considerably exceeds that of any other rodent and shows attenuated decreases in most physiological functions⁸ and has a particular resistance to degenerative diseases,⁹ say cancer, diabetes, cardiovascular, etc.^10,11 Science magazine named the nude mole rat "Vertebrate of the Year" for 2013.⁷

The mole-rats, especially the Spalax species, are always subject to environmental fluctuations,¹² especially with the passage of the seasons, where they show different metabolic behaviors. In winter,¹³ for example, there is a marked variation in the gaseous content of O₂ and CO₂ in the soils, so the interaction of O₂ and CO₂ between the burrows of rats and the surrounding environment is limited. The latter demonstrated the existence of dissimilar differences in hypoxic-hypercapnic stress in different populations of the same species. It is known that the concentration of O₂ decreases, and CO₂ increases with depth.¹⁴ In addition, it was shown that clayey soils notoriously prevent gas exchange between burrows and the surrounding environment.¹³ These conditions are natural to the habitat of the mole rats, which makes their analysis and their influence on the regulatory mechanisms that they perform, especially the tolerance to ROS and the inhibition of carcinogenic processes interesting. 

In previous work,¹⁵ we have demonstrated, at least theoretically, that in the mole-rats there is a critical concentration of high molecular weight hyaluronic acid, which guarantees the self-organization and proper regulation of the process, which ensures high tolerance to oxidative stress and exhibits high resistance to cancer.The main objective of the present work is, from the previously developed model,¹⁵ to explain how they affect the environmental conditions to which the mole-rats are subjected.

Mathematical models represent an adequate way to formalize the knowledge of living systems obtained through a Systems Biology approach.^16,17 The models make the description of essential regularities possible and are useful to provide adequate guidelines for the development of therapies, and so on. For the analysis of this process, the model previously developed by us was used,¹⁵ the network structure shown in Figure 1.

In the model, A represents the oxygen concentration, B the high molecular weight hyaluronan (HA) concentration, X is the concentration of ROS species, Y are the concentrations of the low molecular weight HA, z is the population of the cancer cells and ncp represents the concentration of noncancerous products. The value of each of the constants was taken from our previous work.¹⁵

Due to environmental fluctuations,^13,14 as we discussed in the introduction, parameter A was modified, which is taken as a control parameter, with a function that represents the periodic fluctuation in time as follows:

$\text{A}=1+F{\sin }^2\left(\pi N_a\ast N\ast t\right)$

Where F represents the magnitude of fluctuation of oxygen in the medium,$N_a$ is the autonomous frequency of the original model,¹⁵ where it is considered that there are no oxygen fluctuations. The oxygen concentration of the medium being constant at that time (where A=1 due to hypoxic conditions),¹⁵ N it is the relationship between the frequency of disturbance and the autonomous frequency, understood as the periodicity of the trips in the environment in which they live, and $t$ is time.

If the fluctuations in the concentration of oxygen in the medium are markedly related to the season of the year in which it is measured,^13,14 it was decided to modify both parameters F and N to demonstrate this behavior. A range of variational disturbance was established, ranging from values ​​of F (0.7-1.0) at intervals of 0.1 and N (0.25-2.0) at intervals of 0.25.

The bifurcation diagram (Figure 2) was constructed from the determination of the complexity of the dynamics of the system through the spectrum of the exponents of Lyapunov¹⁸ and the Lempel-Ziv complexity.¹⁹

We use the mathematical methods of chemical kinetics to reduce the network (Figure 1) to a system of non-autonomous ordinary differential equations, equation (1). The equation (1), was solved using the software COPASI version 4.6.²⁰ The numerical method used was LSODA with a relative tolerance equal to 10⁻⁶ and an absolute tolerance equal to 10⁻¹².

$\begin{array}{l}\frac{dx}{dt}=4.7x\left(1+F{\sin }^2\left(\pi N_a\ast N\ast t\right)\right)-xz-x\text{B}\\ \frac{dy}{dt}=x\text{B}-y\\ \frac{dz}{dt}=y-2z\text{B}\end{array}$ (1)

Figure 2 shows the bifurcation diagram based on the determination of complexity across the spectrum of Lyapunov exponents.

Figure 1 The nonlinear network model of mole-rat.

As shown (Figure 2) N as it changes, the relationship between the frequency of disturbance and the autonomous frequency, understood as the periodicity of the trips in the environment in which they live, a wide range of different dynamics is observed, associated to changes in the complexity of the dynamics. It should be noted that a large area of ​​the diagram shows a deterministic chaos-like behavior, which speaks in favor of the robustness exhibited by mole-rats subjected to a hostile environment.²¹

Figure 2 Bifurcation diagram for the eq. (1). The zones with red color represent the crisis states,²¹ the zones in pink color represent the chaotic dynamics,²¹ the lith, and dark blue represent the quasi-periodic states.²¹

Figure 3 shows the dynamic behavior observed during the variation of the magnitude of fluctuation of oxygen in the medium F and N=0.25.

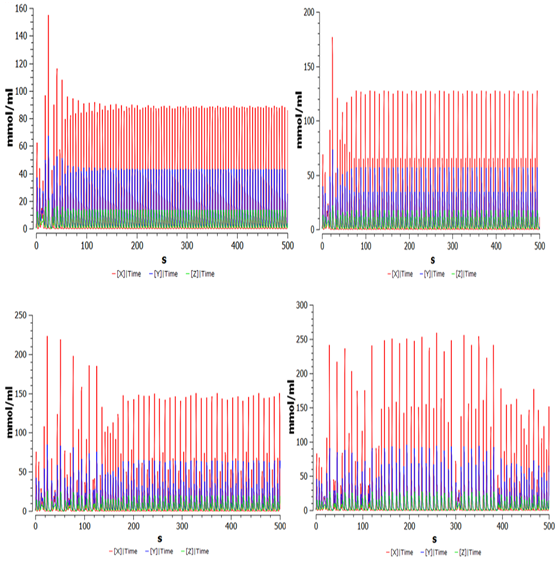
Figure 3 Time series obtained from equation (1), for different values of parameter $F$ and $N=0.25$ ; x is the concentration of ROS spices (red), y is the concentrations of the low molecular weight $\text{HA}$  (blue); z is the population of the cancer cells (green).

It can be seen that, as the magnitude of the fluctuation of oxygen in the medium (F) increases in the same frequency ratio, the population density of reactive oxygen species (ROS), low molecular weight hyaluronic acid (HA) increases progressively. This indicates the adaptability that the system transmits to environmental fluctuations, manifesting itself as a marked increase in the complexity of the system compared to the autonomous model.¹⁵

However, it is observed that the system, to guarantee its adaptability, is still capable of maintaining a constant regulatory action of cancer cells, despite the new hostile conditions of the environment.

On the other hand, the system becomes susceptible to decrease its longevity if the magnitude of the fluctuations of oxygen in the environment increases, and periodically necessary surface trips are not made. That is, the system is under movement constraints, which could indicate transit through a quasi-anoxic environment. This explains why, even in anoxic conditions, mole rats are able almost entirely to maintain their anti-cancer behavior.

Figure 4 shows the dynamic behavior observed during the variation of the periodicity of the trips in the environment in which mole-rats live and the magnitude of fluctuation of oxygen in the medium F is constant. It can be seen that, as the magnitude of the fluctuation of oxygen in the medium (F) is kept at a constant value, while the variation of the periodicity of the trips in the environment N in which mole-rats live, indicates that they are no longer under any restriction of movement, so there will be no significant loss to the tolerance of ROS and guarantees not to pass through quasi-anoxic states that may contribute to the loss of functionality. Once again, the robustness exhibited by the mole rats, the adaptability to the environment, manifested as a marked increase in the complexity of the non-autonomous model compared to the previously developed autonomous model.¹⁵

Figure 4 Time series obtained from equation (1), observed during the variation of the periodicity of the trips in the environment in which mole-rats live $N$  and the magnitude of fluctuation of oxygen in the medium $F$ is constant: x is the concentration of ROS spices (red), y is the concentrations of the low molecular weight $\text{HA}$ (blue); z is the population of the cancer cells (green).

The network-modified model proposed for the mole-rats, qualitatively shows that mole-rates, when subjected to hostile conditions such as variations of the oxygen of the environment, maintain high robustness to environmental changes, which ensures its adaptability to the environment.

The current theoretical framework developed shows how mole rats do not follow the same rules of longevity and aging of nature. We hope that the present study will help to understand the mechanisms of senescence better and contribute to improving our knowledge of Lifespan and degenerative diseases, such as cancer.

Prof. Dr. A. Alzola in memoriam and Prof. Dr. Germinal Cocho, in memoriam, for support and encouragement for this research. One of the authors (JMNV) thanked the CEIICH of the UNAM Mexico for the warm hospitality and the financial support by PREI-DGAPA-2019. Finally, we thank the anonymous reviewers for their helpful comments and interesting suggestions.

The authors declare no conflict of interest.

1. Schosserer M, Grubeck-Loebenstein B,  Grillari J. Principles of biological aging. Zeitschrift fur Gerontologie und Geriatrie. 2015;48(3):285–294.
2. Zhao Y, Tyshkovskiy A, Muñoz-Espín D, et al. Naked mole rats can undergo developmental, oncogene-induced and DNA damage-induced cellular senescence. Proceedings of the National Academy of Sciences. 2018;115(8):1801–1806.
3. Magalhães JPD, Costa J, Church GM. An analysis of the relationship between metabolism, developmental schedules, and longevity using phylogenetic independent contrasts. The Journals of Gerontology Series A: Biological Sciences and Medical Sciences. 2007; 62(2):149–160.
4. Buffenstein R. Negligible senescence in the longest living rodent, the naked mole-rat: insights from a successfully aging species. Journal of Comparative Physiology.2008;178(4):439–445.
5. Jarvis JU, Sherman PW. Heterocephalus glaber. Mammalian species. 2002;(706):1–9.
6. Csiszar A, Labinskyy N, Orosz Z, et al. Vascular aging in the longest-living rodent, the naked mole rat. American Journal of Physiology-Heart and Circulatory Physiology. 2007;293(2):H919–H927.
7. Breakthrough of the year 2013. Notable developments”. Science. 2013;342(6165):1435–1441.
8. Mitchell TW, Buffenstein R,  Hulbert AJ. Membrane phospholipid composition may contribute to exceptional longevity of the naked mole-rat (Heterocephalus glaber): a comparative study using shotgun lipidomics. Experimental gerontology. 2007;42(11):1053–1062.
9. Ruby JG, Smith M,  Buffenstein R. Naked mole-rat mortality rates defy Gompertzian laws by not increasing with age. Elife. 2018;7:e31157.
10. Smith ES, Schuhmacher LN, Husson ZM. The naked mole-rat as an animal model in biomedical research: current perspectives. Open Access Anim Physiol. 2015;7:137–148.
11. Lewis KN, Mele J, Hornsby PJ, et al. Stress resistance in the naked mole-rat: the bare essentials–a mini-review. Gerontology. 2012;58(5):453-462.
12. Ågren UM, Tammi RH, Tammi MI. Reactive oxygen species contribute to epidermal hyaluronan catabolism in human skin organ culture. Free Radical Biology and Medicine. 1997;23(7):996–1001.
13. Shams I, Avivi A,  Nevo E. Oxygen and carbon dioxide fluctuations in burrows of subterranean blind mole rats indicate tolerance to hypoxic–hypercapnic stresses. Comparative Biochemistry and Physiology Part A: Molecular & Integrative Physiology. 2005;142(3):376–382.
14. Griffin AS. Naked mole-rat. Current Biology. 2008;18(18):R844–R845.
15. Triana L, Cocho G, Mansilla , et al. Deciphering the longevity of the mole-rats. International Journal of Aging Research. 2018, 1:13.
16. Magi S, Iwamoto K, Okada-Hatakeyama M. Current status of mathematical modeling of cancer–From the viewpoint of cancer hallmarks. Current Opinion in Systems Biology. 2017;2:39-48.
17. Simeoni C, Dinicola S, Cucina A, et al. Systems biology approach and mathematical modeling for analyzing phase- space switch during epithelial-mesenchymal transition. In Systems Biology. 2018;95–123.
18. Wolf A, Swift JB, Swinney HL, et al. Determining Lyapunov exponents from a time series. Physica D: Nonlinear Phenomena. 1985;16(3):285–317.
19. Lempel A, Ziv J. On the complexity of finite sequences. IEEE Transactions on information theory. 1976;22(1):75–81.
20. Hoops S, Sahle S, Gauges R, et al. COPASI-a complex pathway simulator. Bioinformatics. 2006;22(24):3067–3074.
21. Kantz H,  Schreiber T. Nonlinear time series analysis. Cambridge university press. 2004(7).