MOJ
eISSN: 2573-2919


Research Article Volume 2 Issue 5
Department of Fisheries and Aquaculture, Nigeria
Correspondence: Akange Edward Terhemen, Departments of Fisheries and Aquaculture, University of Agriculture, PMB 2373, Makurdi, Nigeria, Tel 234-703-715-730-5
Received: July 19, 2017 | Published: August 4, 2017
Citation: Terhemen AE, Raphael TAA, Obagye OM. Some length-based determination of the age of Synodontis Schall in Lower River Benue, Nigeria. MOJ Eco Environ Sci. 2017;2(4):218-222. DOI: 10.15406/mojes.2017.02.00038
A Length-based study of the age of Synodontis schall from the lower River Benue was conducted for a period of 12 months (January-December, 2013). Length measurements (cm) were conducted on 963 samples of the fish species during the period of study. Five length-based approaches were used in analyzing the length-frequency data obtained in the 12-month period and the following asymptotic length, values were obtained: Monte-Carlos Simulation, 31.26cm; Bhattacharya’s method, 30.11cm; VBGF, 37.06cm; Powell-Wetherall, 35.59cm and Jones and van Zalinge, 37.06cm. It was noted that the Monte-Carlos and Bhattacharya’s methods were simulative and could have recorded lower values due to individual variability in growth parameters, seasonal oscillation in growth, size-dependent selection, variable recruitment period and large length-class intervals used in grouping length data. It was also observed that Synodontis schall in lower River Benue attained its maximum length at age 3+ suggesting short longevity of lifespan. It was concluded that length-based age study was the most reliable approach in studying fish stocks in the tropics especially in these moments of ecosystem variability occasioned by global warming.
Keywords: Age; Length-Based; Synodontis Schall; Asymptotic Length; Lower River Benue
The uncertain weather and climate regimen imposed by global warming in the tropics has made it even more difficult to assess the age of tropical fishes. This is because there are no clear-cut dry and wet seasons. Temperature which is the major determining factor in the assessment of age in fishes in erratically distributed all through the year and do not account for the rate of growth which is reflected on the hard parts as it is in temperate fishes. In spite of frequent criticism, the methods for the analysis of length frequency data have found, in the tropics, wider applications than the study of skeletal parts, while tagging studies have generally been under-utilized [1]. Fortunately, several numerical methods have been developed which allows the conversion of length-frequency data into age composition [2]. Petersen method (from length-frequency data) is seen as the most-handy method for age determination in the tropics. Many scientific approaches have been postulated by fisheries scientists in determining the age and growth of fish from their length data. These postulations are expressed in mathematical models of Walford [3]; Beverton and Holt [4]; Ursin [5]; Bhattacharya [6]; Ricker [7]; Pauly [1]; Von Bertalanffy [8]. Essential age and growth parameters obtained from these models apart from determining their length-at-age are asymptotic length ( ), growth curvature (K), and so on. Recently, stock assessment has become very popular considering the dwelling concern of depleting tropical stock.
Synodontis schall is one of the most abundant species in the lower River Benue. Known for their hardness and robustness, they can tolerate the wide variation in the lower River Benue. Also, its rate of spoilage at catch is usually not high. These make the species a commercially important fish even though its size may not be really appealing. Studies on the species have become very elaborate among fisheries scientists in the tropics perhaps for these reasons. Abowei and Hart [9] worked on ten species (including Synodontis schall) in lower River Nun; Araoye et al. [10] worked on the age and growth of S. schall in Asa Lake, Nigeria but centered on age determination from hard parts; Akombo et al. [11] also reported on the age and growth of S. schall from the lower River Benue using hard parts (opercula bones). There are no reports on the age and growth of S. schall from the lower river Benue using length-frequency approach. This work is aimed at providing information on some age and growth indices of S. schall from lower Benue with focus on length-frequency approach. This is in view of the unreliability and inapplicability of hard parts and tagging methods respectively in the tropics. Such information is relevant in the formulation of useful policies in the management of the fisheries of lower River Benue especially of the species, S. schall. King [12] noted the difficulty experienced in managing fisheries of this kind of lower River Benue as the fishers are numerous and usually scattered in small communities. The poor coordination of fishermen makes it impossible to monitor their catches for sustainable yield. Also, this work attempts to compare the commonest length-frequency method of age and growth determination to note the variations that exists in their estimations.
Study area
This study was carried out on the lower River Benue at Makurdi. The Lower Benue River is the course of the Benue River that is runs within Benue and Kogi States of Nigeria [13]. River Benue originates from the Adamawa Mountains of Cameroun and flows west across East-Central Nigeria [14].
Commercial catches are landed at three major sites in Makurdi.
Collection of samples
Samples of Synodontis schall were obtained from the fishermen on their return from fishing to the landing sites. This was done forth-nightly for a period of 12 months (January-December, 2013) between the hours of 6-10am. A total of 963 samples were collected during the study period.
Analysis of samples
Monte Carlos Length-Frequency Simulation: this was evaluated from the Fish Stock Assessment Tool (FiSAT II) software. Figures obtained from recruitment analysis, growth parameters, mortality and gear selectivity were automatically used for simulating the life (growth, migration) of S. schall at the time of catch, from one sampling period to the next, until it dies due to natural or fishing mortality. A time series of length frequencies was generated which was presented on monthly basis by their ages [15].
Determinations of Age from Length-Frequencies using Bhattacharya’s Method: this was also determined using the Fish Stock Assessment Tool (FiSAT II) using the model
Where
= were successive frequencies of the same component of a group of fish in a sample (i.e representing age group j) and where Li was the upper class limit of .
From this, the mean of the normal distribution was
while its standard deviation (ϭ) was
where was the constant class size.
Also, a separation index (SI) was computed.
where was the difference between two successive means, and ∆ϭj was the difference between their estimated standard deviations.
The separation of length-frequency samples into their components is an iterative process in that every identified component is subtracted from the remainder of the sample using the Gaussian function,
Where Ni+ referred to the previous set of frequencies and N2i+ the new set of frequencies, less the component identified so far.
The mean length groups as well as their frequencies and standard deviations were generated for each age group after connecting the points. The length-frequencies generated from the Bhattacharya’s method was further refined using NORMSEP which applied the maximum likelihood concept to separation of the normally distributed components of size-frequency samples [15].
Determinations of and K using VBGF: The von Bertalanfy Growth Function (VBGF) was evaluated from the Fish Stock Assessment Tool (FiSAT II) software using ELEFAN I. Lengths of the fish samples were grouped in the class intervals of 3cm and fitted into Length-frequency plot to generate the L∞ and K from the von Bertalanfy Growth Function (VBGF)
Restructured frequencies were used to determine the ages with lines connecting cohorts on the frequency bars [15].
Determinations of using Powell-Wetherall Plot: was evaluated from the Fish Stock Assessment Tool (FiSAT II) software of constant class intervals of 3cm. The computation took into account the smallest length fully recruited by the gear (L', or cut-off length).
Where
from which , and
The and Z/K values were determined from the plot which as well generated the regression function relating the Ḹ - L' and L'(cut-off length) [15].
Determinations of using Jones and van Zalinge Plot: the Jones and van Zalinge plot was also plotted from the Fish Stock Assessment Tool (FiSAT II) software using length frequency-data of constant interval [15].
was determined from the equation:
Where was the cumulative catch (computed from the highest length class with non-zero catch) corresponding to class i and Li was the lower limit of the length class. The slope b was an estimate of Z/K.
Monte carlos simulation of length-frequency
Table 1 presents the results of S. schall in lower river Benue. The simulation of age based on a body length had S. schall living up to age 3+ between the months of May to September which coincided with the rainy season. The age class with the highest frequency was age 1+ which had 242 (25.12%) of the 963 samples analysed during the 12-month study. Age 3+ had the least frequency (1.97%) during the period of study. There was a progression in the length-at-age. The length at age 0+ was simulated as 15.34±2.63 cm, age 1+ as 25.25±3.95cm, age 2+ as 25.25±3.95cm and age 3+ as 31.26±3.24cm. In these simulations, it may be concluded that the was the age at its oldest age (31.26±3.24cm). In corollary, it may also be said that Synodontis schall could live up to age 3+ considering the prevailing ecological conditions of lower river Benue (Figure 1).
Month |
Frequency/ Lengths |
Mean Avg (yr) |
|||
0+ |
1+ |
2+ |
3+ |
||
January |
Frequency |
33 |
37 |
30 |
0 |
Mean±SD |
8.69±8.59 |
14.01±13.68 |
17.78±12.58 |
- |
|
February |
Frequency |
18 |
14 |
18 |
0 |
Mean±SD |
16.67±3.03 |
25.14±4.88 |
29.50±3.09 |
- |
|
March |
Frequency |
13 |
23 |
14 |
0 |
Mean±SD |
19.65±4.34 |
26.85±4.37 |
28.50±3.35 |
- |
|
April |
Frequency |
14 |
18 |
18 |
0 |
Mean±SD |
18.57±2.49 |
27.67±4.73 |
28.94±4.18 |
- |
|
May |
Frequency |
15 |
16 |
18 |
1 |
Mean±SD |
20.90±3.20 |
28.00±5.55 |
29.61±3.27 |
30.50±29.00 |
|
June |
Frequency |
19 |
14 |
16 |
1 |
Mean±SD |
20.39±3.54 |
25.36±6.06 |
27.38±4.98 |
32.50±33.00 |
|
July |
Frequency |
6 |
20 |
19 |
5 |
Mean±SD |
21.50±3.16 |
24.85±4.96 |
29.61±3.49 |
31.30±4.15 |
|
August |
Frequency |
3 |
23 |
16 |
8 |
Mean±SD |
9.50±16.40 |
27.15±3.76 |
28.81±5.12 |
30.50±3.38 |
|
September |
Frequency |
5 |
24 |
17 |
4 |
Mean±SD |
12.10±1.52 |
25.17±4.67 |
28.50±3.78 |
31.50±4.83 |
|
October |
Frequency |
11 |
22 |
17 |
0 |
Mean±SD |
7.95±2.46 |
25.68±3.67 |
26.74±3.96 |
- |
|
November |
Frequency |
11 |
15 |
24 |
0 |
Mean±SD |
13.14±3.67 |
26.17±5.02 |
28.46±4.32 |
- |
|
December |
Frequency |
15 |
16 |
19 |
0 |
Mean±SD |
15.03±3.64 |
26.94±3.97 |
29.76±3.71 |
- |
|
Mean |
15.34±2.63 |
25.25±3.95 |
27.80±3.56 |
31.26±3.24 |
|
Table 1: Monte Carlos simulation of Length-Frequency of Synodontis schall in lower River Benue.
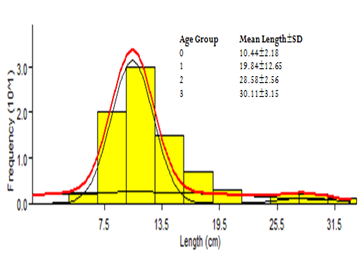
Figure 1: Bhattacharya’s Method of Normal Age Distribution of Synodontis schall in lower River Benue.
Age determination from length-frequencies using Bhattacharya’s method: The Bhattacharya’s method of age determination is presented in figure 1. Age 0+ was determined on the Bhattacharya’s method of age determination to be 10.44±2.18cm; age 1+ as 19.84±2.65cm; age 2+ as 28.28±2.56cm and age 3+ as 30.11±3.15cm. The fish samples with the highest frequency in the length class 8-14cm (Figure 2).
Age determination from length-frequencies using Powell-Wetherall plot: The Powell-Wetherall plot presented in figure 3 estimated the asymptotic length to be 35.59cm. The Z/K was 3.18 while the function was Y=8.50 + (-239)*X (Figure 3).
Age determination from length-frequencies using Jones and van Zalinge plot: The Jones and van Zalinge Plot is presented in figure 4. The asymptotic length was estimated to be 37.06cm while the Z/K was 1.80 (Figure 4).
The asymptotic length of the various methods: The asymptotic length of S. schall in lower River Benue from the various methods used in the research is presented in Table 2. Although it was impossible to subject the asymptotic lengths to an ANOVA test (because they were mean values without replication), it is clear to note that the asymptotic lengths, for VBGF (37.06cm), Powell-Wetherall plot (35.59cm) and Jones and van Zalinge plot (37.06cm) were close to each other in value. The lengths at age 3+ which were estimated at the oldest age of S. schall were considered as the asymptotic lengths, . The values of Monte-Carlo simulation (31.26cm) and Bhattacharya’s method (30.11cm) were comparably lower. The research came up with findings that S. schall in Lower River Benue grew up to three years and attained an asymptotic length ranging 30.11-37.06cm. It can be asserted that there were no tangible variations in the value of the asymptotic length reported by the five approaches. The reports of Abowei and Hart [9] of S. schall having an asymptotic length of 38.7cm in lower River Nun was close to the range of values reported in this work. The variation in the value may be attributed to ecosystem variability in terms of food resource abundance and favorable physico-chemical conditions. Sparre et al [2] reported that growth of fishes differed from species to species and from stock to stock even within the same species as a result of different environmental conditions. It was also observed that the fish attained its asymptotic length within three years (age 3+). According to Lowe-McConnell [16] aquatic organisms at lower trophic levels attain their maximum lengths and sexual maturity within short periods so as to gain the opportunity to raise succeeding progenies to replenish their populations. More so, the compensatory exogenous factors life food abundance, under-exploitation and ideal water conditions that could have enhanced its prolonged lifespan were unfavorable. Alliot et al. [17] and Wassef and El-Emary [18] submitted that apart from endogenous attributes like genotype and physiological conditions, the external environmental conditions as well as habitat resources promotes the lifespan of a fish species. King [19] also attributed the differences in maximum size attained by fish in different water bodies to noise from outboard engines and industrial activities. The asymptotic lengths obtained from the Monte-Carlos (31.26cm) and Bhattacharya’s (30.11cm) methods were both simulative. This could have explained their comparably lower L∞. Isaac [20] reported that simulations from ELEFAN I are often biased due to factors such as individual variability in growth parameters, seasonal oscillation in growth, size-dependent selection, variable recruitment period and large length-class intervals used in grouping length data. Akombo et al. [11] worked on the same species using two different approaches and obtained 28.50cm (Ford-Walford plots) and 20.36cm (at age 3+ from back-calculations using hard parts) while its length at age 4+ (which was the oldest age ) was 21.85cm. El-Kasheif et al. [21] also obtained a back-calculated of the fish in River Nile as 24.93cm at age 3+ while the asymptotic length was calculated as 63.15cm. The values obtained from these works were comparably lower. It may be argued that since values obtained from this work were length-dependent, they may tend to be more reliable as has been earlier confirmed by Sparre et al. [2].
Length-Based Method |
Asymptotic Length (cm) |
Monte-Carlos Simulation (Length at age 3+) |
31.26 |
Bhattacharya’s Method (Length at age 3+) |
30.11 |
von Bertalanfy Growth Function, VBGF |
37.06 |
Powell-Wetherall Plot |
35.59 |
Jones and van Zalinge Plot |
37.06 |
Table 2: Asymptotic Length of S. schall from the various methods.
It was also observed that Synodontis schall in lower River Benue attained its maximum length at age 3+ suggesting short longevity of lifespan. It was also concluded that length-based age study was the most reliable approach in studying fish stocks in the tropics especially in these moments of ecosystem variability occasioned by global warming.

©2017 Terhemen, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.