Preservation and transportation of bulk quantities of oil products in tanks is strictly connected with a creation of safety conditions under its operation. Oil leakage in to environment medium may cause a detriment to it. This is equally attributed to the case when the tank is located on the dry land or at the transportation ships. It is known, that cost of water purification from the oil is reached more than 106 $ if the sea surface is one mile sq. The damage osf tanks wall is possible when the tankers are collided with underwater obstacles, icebergs or other ships. Now in case of such an emergency situation with the tankers, an auxiliary vessel with empty reservoir is called and oil product is pump out from the damaged tank. The span of arrayal time depends on geographical point of the incident and takes from one to a few days. During this time pollution of sea may spared to great scales. There is no garantec of complete protection from oil leakage if the tanker has double hull. Low temperature engineering technology gives a method which may solve the problem of precluding of oil leakage from the damaged wall of ship tanks with en a short span of time .It is necessary to equip each tank-bearer with a cryogenic reservoir containing liquid nitrogen. The outer side of each tank is supplied by flexible vertical tubs which are set up in parallel with interval of 300 mm. The free hanging of the tubs is preventing them from mechanical damage in case of sea incident. So let it consider the process of water freezing around a tube which is cooled down inside by a liquid nitrogen. To simplify the analysis the temperature of wall tube is accepted as constant at the level of 77 K (boiling temperature of liquid nitrogen at atmospheric pressure).
The heat transfer coefficient from the water side is constant αw = 180 Wt/ (m2 K).
The heat transfer process is described by Fourier unstationary differential equation for a tube being cooled inside and immersed in an aqueous medium.
In cylindrical coordinates it looks like this
(1)
Equation (1) is attributed to unlinear unstationary type with variable transfer coefficient, which can’t be solved in quadrature by methods. More fertile results may be obtained on the bases of approximate analytical methods which give result with an desirable accuracy where
is average specific heat accumulation of ice at a temperature
Temperature of phase change of water in to ice, K;
Temperature of wall of tube, K;
The law of heat conductivity change of ice with temperature is correlated by K.D. Timmerhaus et al.1
(2)
Where K = 615.34 W/m – dimensional constant;
T–Temperature of ice, K
heat conductivity of water ice at phase change temperature, W/(m K);
Is density, kg/m3;
r– Cylindrical coordinate, m;
Time of process, s.
An initial and bordering conditions is expressed as
(3)
(4)
(5)
Where
temperature of tube wall, K;
η–Movable coordinates of ice water border, m;
Water temperature, K.
Heat balance on the movable ice water border
(6)
Where L–heat of phase changes (freezing of water into ice), Dj/kg.
The final result of the equation (1) decision without deriving of it is presented at.2 The procedure of deriving of the result provides an introduction of new variable ”V”
(7)
(8)
(9)
Where
outside of the tube, m;
Thickness of ice layer forming on the tube surface, m;
Variable factor office growth rate, m/c2.
This turning the equation (1) from partial derivation to a full of them
(10)
Equation (6) is taking the form
(11)
Initial and bordering conditions will be
(12)
(13)
(14)
Suppose the temperature profiles within the ice lager is expressed as a series
(15)
The second derivative of T(V)
(16)
Taking into account expressions (11, 12, 13, and 14) the final result of the task is expressed.
(17)
Variable factor of growth rate β is found for a accepted time by solving (17). The ice thickness is detcrmed by equation (9). The calculation made according equation tube (17) and (9) revealed that cryogenic temperatures on the wall needs taking into account the temperature dependence of water ice layer (Figure 1).
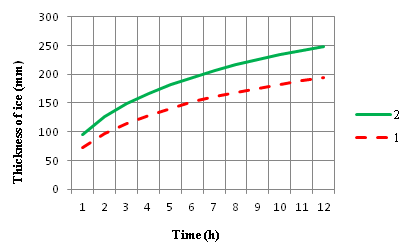
Figure 1 Growth of ice on a flat wall being at cryogenic temperatures and immersed in aqua media (Tw = 278 К, αw = 180 W/(m2 K), Twall = 77 K, radius of the tube r = 0.04 m): 1 – with constant characteristics of ice; 2 – with variable characteristics of ice.


