Topographic maps and Geographic Information Systems (GIS) through the application of spatial analysis tools derived from Digital Elevation Models (MED), constitute a fundamental resource in the management of hydrographic basins and territorial planning. The objective of this work is to delimit flood risk areas by applying DEMs, taking as a case study the El Estero stream micro-basin, San Ramón in Costa Rica, which is located on the left and upper bank of the Río Grande de San Ramon. The spatial analysis allowed us to show all the topographic conditions of the micro-basin and precisely delimit the stream valley, revealing those areas of the micro-basin that are prone to flooding. This research not only shows how the use of DEMs and their derived products allows a detailed study of some of the variables that influence the production of flood sites but is also an indispensable tool in urban planning.

Keywords: Digital Elevation Model (MED), topographic diversity, micro-basin, flooding, El Estero

Digital Elevation Models (MED) are a form of representation of the relief from which the information that is usually extracted from the isolines of topographic maps can be obtained, and other products derived from the DEM, which offer information about the different factors that affect the relief and in this case that cause flooding. Digital elevation models (DEMs) are necessary to map and model natural hazards and risks that are influenced by topography, for example, floods and landslides.

Because water only flows downstream, the flow is channeled by objects that are higher than the water level, elevation information is used to model the flow of water and determine possible flood areas in the event of flooding flood. Slope is the decisive factor in surface runoff and in the direction of stream courses, hence DEMs are a fundamental tool to detect flood-prone regions. In general, the rains, being liquid in this case because it is a tropical country where snow does not fall like Costa Rica, always go from areas with a certain contrast of initial relief in their area of origin to the lowest place.

Slope can be easily obtained from DEMs, any standard remote sensing software provides tools to automatically obtain a slope image from a DEM. According to research carried out in Germany, a 30m spatial resolution DEM derived from X-band data from the STRM (Shuttle Radar Topography Mission) mission was used in combination with multi-temporal NDVI trajectories derived from 5m resolution RapidEye optical satellite images, to automatically detect large area landslides and flooding.¹

This MED was successfully applied in a study area in Kyrgyzstan with an average landslide of approximately 13,000m². According to the study authors, further methodological development is needed to adapt the approach to regions where the geography differs greatly from conditions in Asia.²

With this information, inventories of temporary floods and landslides and other geographical characteristics can be generated. With this information, various characteristics of the land's relief can be regularly monitored, including socio-natural risks, such as floods and landslides.

Furthermore, DEMs are necessary for ortho rectification (georeferencing) of satellite images. Satellite images taken at different viewing angles can only be compared when they are ortho-rectified (georeferenced), otherwise the pixels do not align.

One of the starting points for the geographical analysis of the terrain is to have a digital elevation model (DEM) with adequate precision. The work can be difficult if altitude data is not available for the territory to be analyzed, in many cases prior sampling of this data is necessary, using remote sensors placed on airplanes, drones or satellites in Earth orbit. RADAR data and its version of LIDAR are some of the most used due to their ability to penetrate vegetation, more than shorter wavelength radiation, such as visible or ultraviolet light. Although in terrain almost devoid of vegetation, visible light is enough to obtain elevation data if the sensor is correctly calibrated for it.

In the case of the El Estero micro-basin, elevation data is available through the contour lines of the SNIT (National Territorial Information System) of the IGN (National Geographic Institute of Costa Rica),³ available throughout Costa Rica. There is also a DEM for the entire country with a precision of 10 meters, hydrologically corrected, prepared by the TEC (Tecnológico de Costa Rica),⁴ shown in Figure 1 and using a color scale. A variety of territorial data can be accessed via WMS (Web Map Service) directly from GIS software such as QGIS or ArcGIS, allowing you to import and view vector or raster data, such as contour lines, elevation levels or orthophotos at different scales.

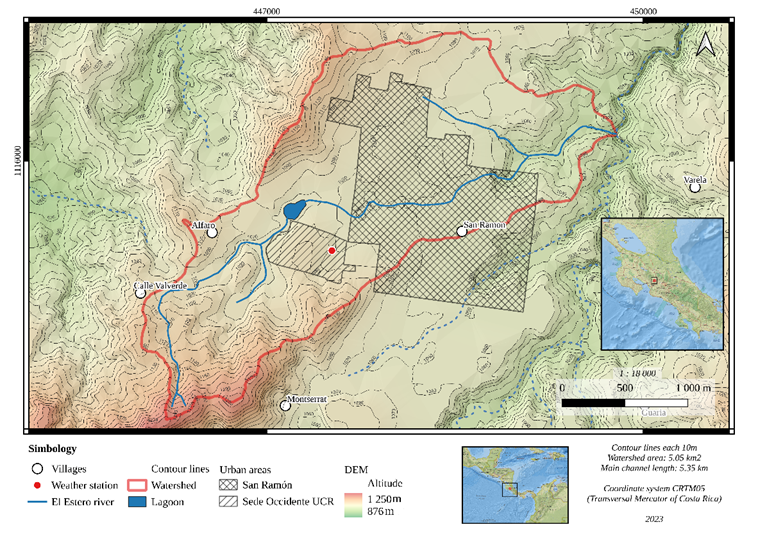
Figure 1 DEM with 10 m precision for all of Costa Rica visualized in QGIS.
F. Own Source. Own elaboration, with data from TEC-CR,2024).

Thus, several digital elevation models use a GIS raster data format as a spatially explicit input data structure. This situation arises from the 1980's when digital elevation models (DEM) were more commonly used to generate topographically derived variables as models of the physical characteristics of a watershed. The raster format represents spatial features as a quasi-continuous surface comprised of cells, usually equidimensional, containing numerical values that represent topographic diversity. Fallas⁵ notes that physically based models have potential for the prediction of land use changes and have potential for hydrological predictions in basins, given the slope of the river courses and the topographic diversity of the micro-basin.

The parameter calculation involving the derivation of topographic and land cover data, e.g. Surface slope, physical parameters of the basin, are of importance, since they show the topographic irregularity. The union of a GIS and digital elevation models with which they still share a common data structure, but the model operates outside of the GIS.⁶

Additionally, GIS can be used to facilitate the visualization and display of exemplary results, which is especially advantageous for surface runoff from the El Estero stream micro-basin.

Interpolation

Interpolation involves estimating missing data from known data. In building models, such as DEMs, it is a necessary technique to fill in missing information and provide a surface represented uniformly in space. There are various interpolation methods, such as SPLINE, IDW, TIN or Kriging, which use various algorithms already preconfigured in Geographic Information Systems (GIS) analysis software and other mathematical analysis programs. In this case, TIN and IDW techniques were applied to create elevation models from contour lines.

TIN

The TIN (Triangular Irregular Network) is a very common way to build an elevation model. It involves filling in the missing elevation data through triangulation from the known points, generating a triangulation network. TINs are based on the analysis of neighboring points, making it a local interpolation method.

The TIN creates a network of triangles according to the Delaunay triangulation, where it is true that the circumcircle in each triangle (circle that passes through the three vertices of the triangle) does not contain more vertices than those that form that triangle.⁷ Two vertices are connected by a Delaunay triangulation if their Thiessen polygons (or Voronoi polygons) share an edge and Delaunay triangulations can be derived from Thiessen polygons.⁷ So, there is the unique property that no point, of the finite set of points in the plane, is contained in the circumcircle of a Delaunay triangle.⁸

As Lloyd⁷ indicates, triangulation has advantages over other methods, “A key advantage of TINs over raster-based representations is that the sampling density can be varied depending on the nature of the topography. “Samples are generally taken from marked breaks in the slope and there tend to be a greater number of observations in areas with more variable elevations and fewer samples in relatively flat areas.”

IDW (Inverse Distance Weighting)

IDW is Inverse Distance Weighting and is the most widely used of the weighting methods. This interpolation method is deterministic, since it uses only known values in its calculation, it does not resort to probabilistic methods such as kriging.⁹

As Lloyd⁷ indicates, for its calculation the following is considered:

$\widehat{z}(S_0)=\frac{{\displaystyle {\sum }_{i=1}^{n}z(S_i)d_{i0}^{-r}}}{{\displaystyle {\sum }_{i=1}^n{d}_{i0}^{-r}}}$   (1)

where the prediction made at location S ₀ is a function of the n neighboring observations z (S_i ), with i = 1, 2, …, n.; r is an exponent that determines the distance assigned for each of the observations. Finally, d_i0 is the distance by which the prediction location (S₀ ) and the observation location S _i are separated.

So, when the exponent r increases, the weight assigned to observations at greater distances is reduced. Consequently, as r increases the predictions become more like nearby observations.

Hydrological correction of DEMs

For both generated DEMs, a correction algorithm must be applied that seeks to eliminate anomalies in the interpolation that produce gaps or artificial “poking” that can lead to unwanted errors, if that generated DEM is used for hydrological analysis, such as the preparation of a surface drainage network. To do this, missing or abnormally low data are filled in according to another interpolation method, normally a SPLINE, as used by GRASS GIS and incorporated in QGIS.

Works such as those by Tarboton¹⁰ analyze the implications and possibilities of improving methods for obtaining flow directions in DEMs, their use to correct the computational calculation algorithms incorporated in GIS software and minimize errors in hydrological modeling.

The method itself used by the QGIS (and GRASS GIS) algorithms according to Jenson and Domingue,¹¹ the computational procedures so that the algorithm can fill the data and avoid points with depressions, generally resorting to the calculation of nearest neighbors to fill with the lowest value to the set of cells (pixels) and thus level the values of the area with depressions.

To calculate an average of nearest points (neighbors), a procedure is followed as mentioned by the ESRI documentation (November 8, 2024).¹²

$ANN=\frac{{\overline{D}}_o}{{\overline{D}}_E}$   (2)

ANN (Average Nearest Neighbor) is equal to the observed distance between the specific distance of each cell and its neighbors. At the same time,

${\overline{D}}_o=\frac{{\displaystyle \sum _{i=1}^n{d}_i}}{n}$ ${\overline{D}}_E=\frac{0.5}{\sqrt{n/A}}$   (3)

Where D_o is the average distance observed between each point and its close neighbors, which is calculated as the sum of the distances between the number of cells or points (n). Y D_E which is the expected average distance between the points considering a random pattern, calculated by dividing the constant 0.5 by the square root of the division by n (total number of points) and A which is the minimum rectangular area that surrounds the points .

Topographic Convergence Index (TCI) or Topographic Wetness Index (TWI)

Some GIS software, such as QGIS and SAGA GIS, use an index to estimate the accumulation of surface runoff fluxes over the terrain, from a DEM. The TCI (Topographic Convergence Index) is also called TWI (Topographic Wetness Index) or CTI (Compound Topographic Index), it is a hydrologically based index that seeks to measure the tendency of a cell (pixel) or area to accumulate and retain water under conditions seasonal (Pennsylvania State University, 2020). For its construction, the work of Tarboton¹⁰ and his D-Infinity model was used to determine the contributing areas. Below is the calculation of the index:

$TWI=ln\left(C_A/S_{\beta }\right)$   (4)

So, the TWI (Topographic Wetness Index) corresponds to the natural logarithm of the C _A (contributing area) between the slope angle S _β . The index makes a balance between the area contributing to capturing surface water, with the slope angles that tend to evacuate that water.¹³

DEM

Based on the contour lines with data every 10 meters, an interpolation was first developed using the TIN (Triangular Irregular Network) method, which gave good results. Figure 2 shows the resulting DEM with this method. A background hillshade (relief layer) was placed on the DEM for greater contrast and better appreciation of the contours, the presence of polygons is noticeable, which is due to the nature of the TIN method, the precision of the contour lines and the analysis scale.

Figure 2 DEM prepared using TIN.
Source. Own elaboration, 2024

The DEM prepared through TIN triangulation shows an adequate representation of the terrain, being especially effective in the most irregular or mountainous areas. It achieves smooth modeling between contour lines and almost does not tend to create terraces or flattening between them. Some errors can be identified in the flattest areas or in the largest depressions (river channels) where polygons tend to be generated that do not correspond to the reality of the terrain.

This elevation model was hydrologically corrected by filling in possible artificial sinkholes. The objective of this is to avoid “wells” or accumulations of runoff, if the DEM were to be used to estimate drainage networks or any other aspect of hydrological modeling.

Using the IDW interpolation method, another DEM was generated as a comparison of the interpolation methods. The following Figure 3 shows the result:

Figure 3 DEM made using IDW.
Source. Own elaboration, 2024.

In this case the calculation takes much longer, resulting in a DEM that tends to be stepped, following the pattern of the contour lines that were used to interpolate. In general, the representation is good, but it tends to generate terraces between contour lines. Different parameters were tried for the search radius for nearby neighbors, giving better results with 20m. For subsequent calculations, it was decided to choose the DEM generated from the TIN network better since it did not present the problem of terraces between contour lines. So, the following Figure 4 presents the final elevation model for the micro-basin, with which the terrain profiles and other calculations are prepared.

Figure 4 Elevation map for the Estero micro-basin.
Source. Own elaboration, 2024

From this final product it can be noted that the topography of the land is irregular, especially towards the riverbeds. But in the case where the central urban area of San Ramón is located, the slope is reduced, and this constitutes an advantage in the location of the city. However, with urban growth and lack of space, buildings have tended to be located on land with greater slopes and, therefore, more unstable.

The DEM can be used as an urban planning tool to avoid construction in disaster risk areas, thus anticipating future material damage and possible negative effects on the population.

3D model

Using the DEM interpolated by TIN, the following three-dimensional view was created for the micro-basin and its surroundings. The red dot indicates the location of the San Ramon meteorological station. Much of the land corresponds to areas of relatively little slope, with exceptions towards the channels of the El Estero stream, in the lower part of the micro-basin and in the upper part (Figure 5).

Figure 5 3D view of the El Estero micro-basin.
Source. Own elaboration, 2024

The shape of the micro-basin is elongated. The size of the El Estero micro-basin in its little more than 5 km, the main channel (El Estero ravine) shows a regular layout, with few curves and a relatively constant slope, with exceptions in the lower part of the channel where the terrain does It is more rugged, forming a small canyon.

Terrain profiles

To get a better idea of the topography, four profiles were drawn in different directions within the micro-basin. These are shown in the following Figure 6.

Figure 6 Terrain profiles within the micro-basin.

Profile A begins from the highest part of the micro-basin, with 1254 m, in a straight line towards the river valley of the El Estero stream (the depressions in the channels can be seen) until ending at the other edge of the basin. In total, almost 4 km of profile are covered.

Profile B shows another section across the width of the micro-basin, crossing an important urbanized area. It begins from the lowest part of the micro-basin, at the mouth of the El Estero ravine, and ascends to one of the mountainous edges of the valley, tracing a straight line. In the profile you can see the small depressions that correspond to the passage through the channel of the stream and one of its main tributaries.

Profile C seeks to cut perpendicularly the El Estero ravine, covering a section across the width of the micro-basin. The depression of the channel can be seen very clearly, as well as the difference in altitude between the two edges of the valley, the one with the highest altitude in a mountainous section with a steeper slope, while the one with the lowest altitude is in an area with a lower slope and which is also very urbanized.

The outline of profile D corresponds to the follow-up of the main channel of the El Estero stream. It constitutes an irregular line that allows you to have an idea of the changes in slope along the course of the watercourse. A greater slope is noted in the upper part of the route, just after the source of the waters, to later reduce considerably towards the lake area and the most urbanized part of San Ramón. It ends again with a considerable increase in the slope, with a waterfall (Figure 7), near the junction with one of the main tributaries, and ends its journey through an area of significant slope leading to the Río Grande de San Ramon. It covers a total of just over 5.2 km.

Figure 7 Waterfall of the El Estero river, in one of the steepest areas.
Source. Own elaboration, Data from Google Earth. 2024.

Identification of steeper sites

The following slope map shows the places with the greatest slopes within the micro-basin and its surroundings, it was prepared from the DEM. The slope is shown in degrees, with dark blue colors being almost flat terrain or with a low slope (less than 4°), to green-yellow colors corresponding to intermediate slopes (about 15° to 25°), to the colors orange red that correspond to steep slopes (more than about 30°).

In Figure 8, at least two areas with significant slopes can be identified. The first (A on the map) is the mountainous area in the lower left part of the image, near where the El Estero ravine originates. In this area there are slopes that go up to 29 degrees in the most irregular parts, although the majority it is between 10 and 15 degrees.

Figure 8 Estero micro-basin slopes and surroundings.
Source. Own elaboration, 2024.

The area with the largest topographic accident in the micro-basin corresponds to the second highlighted area (B on the map), which is located towards the edges of the urban area of the city of San Ramón. Here there is a maximum slope of up to 44 degrees, a steep terrain that coincides with the bed of the El Estero ravine and that tends to form a small waterfall or waterfall.

Other notable areas are the foothills region in the central-northern part of the micro-basin (denoted with a letter C on the map), where the slope reaches values between 10 and a maximum of about 19 degrees. And a fourth area just above the mouth of the El Estero ravine in the Grande de San Ramón River (denoted with a D on the map) where there are slopes of a maximum of 29 degrees, but the majority is between 13 at 23 degrees.

In general, this confirms that the margins of the El Estero ravine, as well as the most mountainous areas of the foothills, are those that present the conditions with the greatest slopes. Although there are also large areas where the slope is very low (dark blue colors on the map) and these, coinciding with the channel of the stream, may present a risk of flooding during floods due to excess rainfall.

Areas with flood potential

The areas near the bed of the El Estero ravine that have lower slopes or are very steep, have the potential to suffer flooding. The lagoon area and its surroundings present some of the greatest risks of flooding. Also, in the area near the mouth of the stream, just after the steep area that forms the waterfall, there is a possible accumulation of flows because the channel is very narrow just a hundred meters before the mouth.

One way to estimate possible regions of surface runoff accumulation is through the Topographic Convergence Index (TCI) or Topographic Wetness Index (TWI). Using the SAGA GIS algorithms, the following result was obtained for the micro-basin and its surroundings (Figure 9).¹⁴

Figure 9 Topographic convergence index.
Source. Own elaboration, 2024.

The highest values of the index (more intense blue colors) tend to coincide quite well with the locations of rivers, streams and minor water courses, giving a very good idea of the behavior of surface water on the ground. However, there are places where the index calculation algorithm has problems; these places coincide with flatter regions where it is more difficult to predict the behavior of the runoff.

From the TCI results, the following areas with flood potential can be identified, all of them on the margins of the Estero ravine (Figure 10).

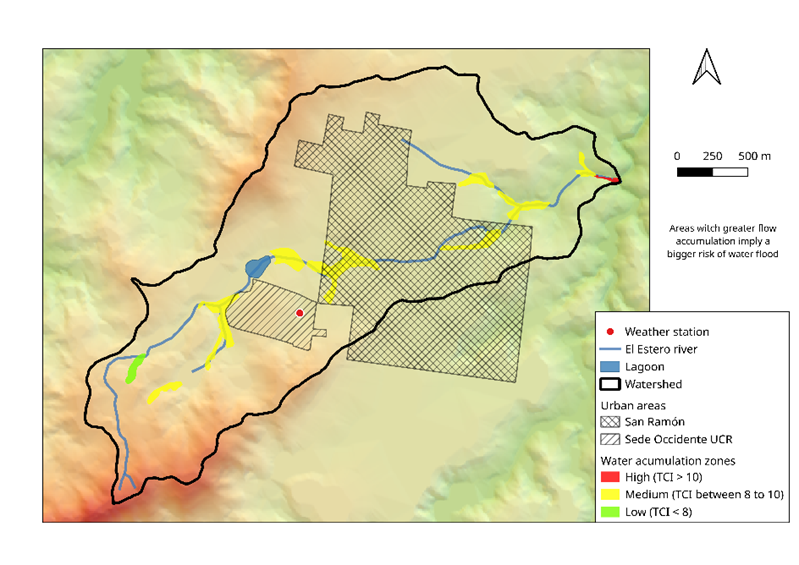
Figure 10 Areas with greater flood potential.
Source. Own elaboration based on field work and satellite images. 2024.

Several areas can be identified (the green, yellow and red polygons) with a flood potential given the accumulation of surface runoff according to the TCI index. These were classified as low (an index less than 8), intermediate (a TCI with values between 8 and 10) and high (TCI greater than 10). Some areas do not exactly coincide with the outline of the El Estero stream, especially within the urban area of San Ramón, this is because part of the channel of the stream has been practically buried by buildings and its recognition is almost impossible from aerial or satellite images.

Most of the areas were classified as intermediate in the potential risk of flooding, which implies that the possibility of being affected during the medium o high flows of the Estero stream and can be considered sufficient to take preventive measures, to avoid a flood situation risk that could lead to a disaster.

The area with the greatest flood potential is in the lowest part of the micro-basin, near the mouth of the El Estero stream. The necessary conditions are in place so that a large part of the water captured by the micro-basin ends up passing through a very narrow part of the channel, generating a funnel effect that enhances the force of the water. This situation is worrying if one considers that in that area there is an urbanization called Bajo Tejares, with homes that are practically located next to the stream bed (Figure 11).

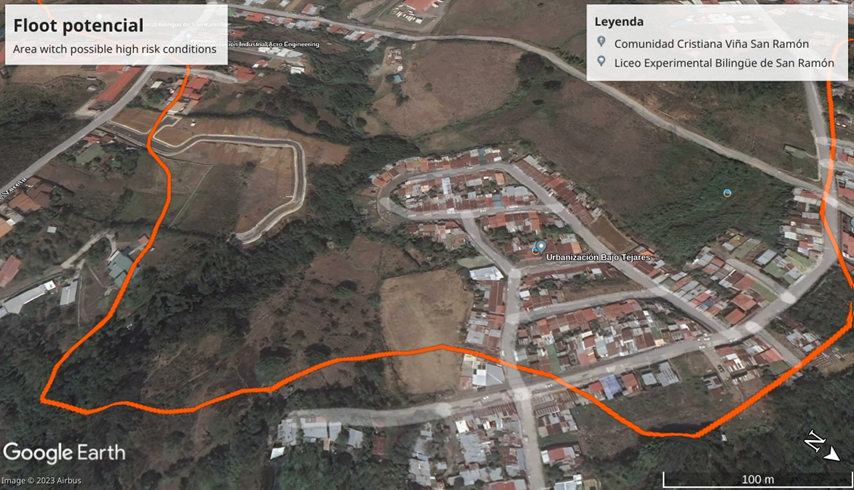
Figure 11 Bajo Tejares houses with high potential for flooding.
Source. Own elaboration, 2024, with data from Google Earth.

You can see the orange line that indicates the limit of the microbasin. You can notice the location of the urbanization next to the creek bed (area with the highest concentration of trees in the center of the image). Possibly the urbanization should have retaining walls in the part closest to the stream.

Digital elevation models summarize physical reality and simulate the complex behavior of rainfall, according to the topographic characteristics of the relief in a simplified manner. This is basic to understand in this case the appearance of floods in the El Estero stream, where the hydrology of the micro-basin is represented as a physical system without any random component.

The digital elevation models applied in this research show the spatial variations of the micro-basin, especially at the altitudinal level. This allows us to visualize not only the areas where greater and accelerated surface runoff can occur, but also the areas where flooding occurs. These digital elevation models show the diversity of scenarios that produce greater runoff, as well as those that have excess precipitation.

The main hydrological processes that occur in the micro-basin are represented schematically or cartographically. Therefore, the use of DEMs and their derived products allows a detailed study of some of the variables that influence the production of floodable sites.

According to Quesada,¹⁵ historically the city has shown different flooding problems after intense rainfall. However, two main situations can be differentiated. On the one hand, the historic center of the city presents superficial runoff on the streets, some laid out on old river courses and on commercial and public facilities such as bus stops. On the other hand, outside the historic center, the occupation of flooded spaces either on the embedded plains (near the Municipal Stadium, Farmer's Fair, municipal gymnasium or bus stops) or on those that belong to flat sites where residential areas are located. (Margins of the stream, part of the El Progreso residential area), in which significant volumes of stagnant water are generated in different neighborhoods and communication routes of the city.

In any case, both situations are related to the risk of material losses, such as homes, loss of assets such as furniture, appliances, vehicles. While, in the occupation of new spaces, without precedent, material losses are related to damage to homes regardless of the social condition of the exposed population. Depending on the distribution of water courses, streams and lagoons that the city of San Ramón and its surroundings have.

The city of San Ramón and its surroundings is affected by flooding in certain years, especially in seasonal periods during the La Niña episode.¹⁵ Its spatial growth towards the interior of the flood valley towards the banks of the stream has generated many floods from 1900 to 2000.¹⁵ and, during the last 24 years, such is the case of the rainy period of the years 2011, 2015, 2022, 2024. The urban location around the El Estero stream is at continuous risk of suffering from flooding and waterlogging.

In relation to the above, it can be stated that the use of DEMs is of vital importance to know the following situations: delimitation of flood areas, floods due to the floods of the El Estero stream and the Caballero streams and another that has no name, as a result of the intense local rainfall and the flooding caused by intense rains, which can be increased by the flooding of the main stream that, by saturating the system, makes it impossible to drain the fallen water.

The DEMs and the spatial analysis tools of geographic information systems constitute a fundamental resource in decision-making and in the generation of risk maps that serve to make decisions regarding prevention measures that prevent growth of cities in risk areas. Making decisions about acting on protocols if floods occur such as the evacuation of people. Making decisions on engineering works that mitigate risks, such as expanding the channel of the stream, and the expansion of a lagoon that is located upstream of the main city with its respective dam that serves as support as the intensity of the floods grows rains and the flow of the stream.

Any measure or methodology considered must consider the entire system (from the source to the mouth), promoting the dynamic balance of the currents through the increase of the native vegetation of the area, both in the upper part, and on the banks and margins of the river on the whole upper part before start San Ramonʹ city. As well as techniques of stabilization of banks and implementation of diffuse and limited works of regulation and artificial restoration.

Due to its topographic and geological characteristics, the micro basin has steep slopes. A land use with volcanic soils and a lack of water management protection, especially in the upper part. This affects its middle and lower sectors causing flooding during certain years when the rainy season is intense, from May to October. In the upper part because of the strong expansion of the population, the construction of housing and urbanizations has increased. Undoubtedly, this has caused and is causing intense soil erosion. This situation in fact has a destination the main channel of the El Estero stream, propitiating the filling of a lagoon that is in middle part before the El Estero stream comes to the San Ramon city. Such water erosion in the micro-basin is characterized by the continuous repetition of a gradual pattern of slopes, ranging from 30 to 60% in the steepest parts to 3% in the middle parts of the micro-basin (USDA, 2014).

Most of the mapping of rural and urban areas that affect, in this case, the El Estero river basin, was done with remote sensing and GIS (geographic information systems) techniques. In fact, this research constitutes an important contribution to the planning of the micro-basin and other future studies in watersheds, since techniques were applied to extract information on land cover from satellite images obtained by remote sensing. This is how it not only allows us to know the amount of area under different land use covers, but also the floodable area. The research is a planning tool for flood control and as a starting point in local municipalities as a sectoral planning instrument.¹⁶

The author acknowledges the support of Ricardo Prado Garro, who helped me making figures. Finally, the author would like to thank the three anonymous reviewers for their valuable comments and suggestions.

I gratefully acknowledge the University of Costa Rica for their financial support. Particularly, the Vicerrectoría de Investigación and Coordinación de Investigación through the research project 540-B8-053.

None.

1. GTZ (Cooperación Técnica Alemana). El SICA y la Cooperación Alemana lanzan plataforma regional de datos forestales geoespaciales. Secretaría General del Sistema de la Integración Centroamericana. SICA. 2014.
2. Behling R, Roessner S, Kaufmann H, et al. GFZ German Research Center for Geosciences. Automated spatio-temporal landslide mapping over large areas using rapid eye time series data. Remote Sens. 2014;6(9):8026–8055.
3. National Geographic Institute of Costa Rica. San José, Costa Rica.
4. TEC-CR (Instituto Tecnológico de Costa Rica. Digitalización de las primeras hojas cartográficas de Costa Rica fomenta investigación y conservación de bosques. Informe técnico. Centro de Investigación e Innovación Forestal. 2024.
5. Fallas J. Digital elevation models: theory, interpolation methods and applications. 2007.
6. Maidment DR. Handbook of Hydrology. New York: McGraw-Hill; 1993.
7. Lloyd CD. Local models for spatial analysis. CRC Press; 2011.
8. Romero N, Barrón-Fernández R. Validation of Delaunay triangulation using conformal geometric algebra. Computing and Systems. 2016;20(4):789–798.
9. Paredes Hernández GU, Salinas Castillo WE, Martínez Becerra X, et al. Evaluation and comparison of deterministic and probabilistic interpolation methods for the generation of digital elevation models. Geographical Investigations. 2013;(82):118–130.
10. Tarboton DG. A new method for the determination of flow directions and upslope areas in grid digital elevation models. Water Resources Research. 1997;33(2):309–319.
11. Jenson SK, Domingue JO. Extracting topographic structure from digital elevation model data for geographic information system analysis. Photogrammetric Engineering and Remote Sensing. 1988;54(11):1593–1600.
12. ESRI. How average nearest neighbor works. ArcGIS Pro. 2023.
13. Pennsylvania State University. PSU DEP Topographic Wedness Index (TWI). Pennsylvania Spatial Data Access (PASDA). 2020.
14. Conrad O, Bechtel B, Bock M, et al. System for Automated Geoscientific Analyzes (SAGA) v. 2.1.4, Geoscientific Model Development. 2015;(8):1991–2007.
15. Quesada 2003 M. Chronological analysis of the overflows of the Quebrada Estero, San Ramón. Current Thought Magazine. Vol.4. N ⁰ 5. University of Costa Rica. 2003:35–41.
16. GFZ Helmholtz Center Potsdam. Digital elevation model for flood and landslide detection. National Geosciences Research Center. Germany. 2014.