The observed loss of biodiversity calls to create a general theory of ecological physics for better understanding of the events. Due to the inseparable mutuality of organism and environment, ecological physics should combine biophysics (physics of organisms) and environmental physics. We guess that a general theory of ecological physics should include as an abstract physical description of an ecosystem and a tool for its transparent (“white box”) modelling. Such a theory should have a system of basic axioms. Here we demonstrate that logical cellular automata allow to create transparent models of ecosystems. The system of basic axioms of the general theory of ecological physics performs the role of the cellular automata rules. We believe that such a transparent mathematical modelling from the first principles is very promising not only for the ecology, but also for modelling of any complex dynamic systems.

Keywords: population dynamics; white–box modelling; ecological physics; resource competition; conservation biology;, cellular automat; biodiversity

Advantages of the cellular automata modelling. The discrete nature of the real world is naturally to model using discrete mathematics. Cellular automata are the most effective mathematical tool for creating discrete models of complex systems. Logical cellular automata are most effective for individual-based modelling in terms of local dependencies. A particular advantage of the individual-based cellular automata models is that they are able to reflect holistic spatial-temporal mechanisms of dynamic interrelations among all levels of population ecosystem - between individuals and their mini habitats and between their mini habitats and the whole ecosystem (macro habitat). The advantages of deterministic cellular automata models are in clarity of their cause-effect relationships, the absence of rounding errors (accuracy), in the simplicity of setting boundary conditions, solvability and holistic relationship of local and global characteristics of models, a detailed mapping of spatial-temporal events. An important feature of this modelling approach is the need for formulation of adequate axioms, based on properties of modelling objects. Correct formulation of the basic interpretations requires a deep and holistic objective knowledge of simulated phenomena. The lattice size, initial cell-states pattern of the whole cellular-automaton field (initial pattern), the type of a neighbourhood and the rules of transitions between states of elementary cell are the key parameters in the cellular-automata modelling. The presented here method can be used in different areas of modelling of competition of agents of any nature. The deterministic cellular automata modelling may be considered as a simple universal inference automaton of mechanistic insight into studied phenomena as it is based on a detailed visualisation of dynamics of all interrelated processes of a complex system under study.

A white-box cellular automata modelling is the most direct way to gain a mechanistic insight into a complex system under study. The main problem of such modelling is a creation of adequate axioms. . Let us formulate our understanding of white-box model. White box (‘clear box’, ‘glass box’, ‘open box’) model has a ‘transparent walls’-all events at all levels of the simulated dynamic system and at all stages of its dynamics are directly visible. White box model directly shows mechanistic mechanisms of the studied phenomena. It allows to obtain a new physical understanding of the studied system and to predict its future development. We consider the cellular automata method developed in this study as the white box modelling. A deterministic, individual-based logical cellular-automata method developed in this study is the most suitable tool for search of the mechanistic mechanisms of complex systems. It is the white-box modelling method based on physically interpreted ecological axioms. These cellular automaton works as a visualising inference automaton of mechanistic insight into studied phenomena. It provides reducing of complex holistic dynamics of inter specific competition to the level of simple logical axioms. Deterministic, individual- and logic-based cellular automata allow creating white-box mechanistic models of complex systems. This approach allows us to naturally decompose the complex system to the homologous constituent elements, to define the possible states of these elements and transitional logic between these states, taking into account the local conditions of each individual element. The key stage of the cellular automata modelling of a complex system is a formulation of physically adequate axioms. These axioms must represent the highest possible degree of physical generalization of a studied complex system. The necessity of adequate basic understanding of a research area is the main difficulty here. A system of axioms created on the basis of this fundamental understanding is used for formulating rules of automatic logical deterministic inference of white-box models. Here we introduce a physics-based semantics (ontology) of our ecosystem models. Further, we transform this semantics to a set of axiomatic cellular automata rules. An elementary object of our models is a micro ecosystem. This is the basic ideal "self-moving" object of our models. Autonomous dynamics of this object is characterized by a set of states, and the diagram of their sequential change in accordance with the principles of the extreme. Following Tansley, we consider individuals with their ‘‘special environment, with which they form one physical system’’.¹ A microhabitat is the intrinsic part of environmental resources of one individual and it contains all necessary resources for its life. It is an intrinsic part of all environmental resources and conditions per one individual. The high-grade (‘‘fresh’’) energy flow of solar radiation provides an individual’s life in a microhabitat. The flow of lowered-grade (‘‘used-up’’) energy which is produced during an individual’s life goes into the cold space and also provides the conditions for an individual’s life in a microhabitat. A living organism is not able to function without the heat output to a ‘‘refrigerator’’. Ultimately, the cold space performs a role of the refrigerator. A working cycle of a micro ecosystem’s processes represents a closed circle, which includes occupation of a microhabitat by an individual and restoration of used resources after an individual’s death. A micro eco-system, includes a single microhabitat and is able to provide a single accommodation of one individual, but it cannot provide its propagation. This is due to the fact that after an individual’s death, its microhabitat goes into a regeneration (refractory) state, which is not suitable for immediate occupation. A minimal ecosystem, providing a possibility of vegetative propagation of an individual, must consist of two microhabitats. In our models vegetative propagation is carried out due to resources of an individual’s microhabitat by placing a finished vegetative primordium of a descendant in a free microhabitat of an individual’s neighbourhood.

A principal feature of our white-box modelling of ecosystem dynamics is the closure of all interactions of an individual with its intrinsic micro-environment at the level of micro eco-system. This closure allows to consider a micro eco-system as an autonomous object. Spontaneous dynamics of a micro eco-system is modelled as transitions between the states of a lattice site. Transitions between the states are accompanied by use of free energy. The free energy is used to ensure the livelihoods of individuals (the high-grade energy of solar radiation) and to maintain processes of the limiting resources recovery during a regeneration state of a microhabitat (energy of solar radiation and energy of organic matter of dead individuals). An individual of the dominant species has greater ecological fitness and wins in a direct conflict for resources for propagating. It has the most effective ability of capturing and using free energy and other limiting resources. The first and the main problem here is to create cellular automata axioms that will reflect physical nature of real system behaviour. If axioms are incomplete or incorrect than all results of the model will be at least questionable. But if all axioms are complete and correct than all predictions of the model will be adequate, mechanistic and obvious. It looks easy, but it is the main problem of many very technically complicated models. Creation of cellular automata axioms requires a holistic physical understanding of a real system and its idealization. This is a deductive top-down step of a modelling (Figure 1). If axioms are complete and correct then there is no problem to create a cellular automaton which will work as a logic machine of bottom-up automatic inference of results of a complex system dynamics.

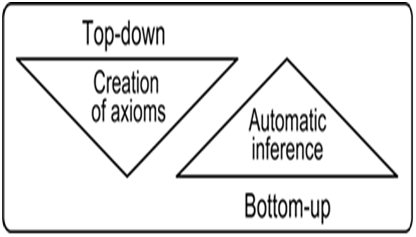
Figure 1 Top-down – bottom-up scheme of the white-box modelling. The first step is a deductive top-down creation of axioms and the second one is a cellular automata automatic inference that realizes a bottom-up approach.

Here we demonstrate white-box cellular-automata models of ecosystem dynamics. They work as the state machines and have maximum visibility. On the basis of formulated axioms we may construct different situations of competitive relationships between closely related species. The model let us to observe and investigate consumption and regeneration of resources in ecosystem, population dynamics and population waves. The cellular automata modelling of eco-system deterministic cellular automata were used for modelling the spatio-temporal dynamics of simultaneous colonisation of a small ecosystem by two tropically identical but fitness different competing species. An integral ecosystem (macro habitat) is modelled by a whole cellular automaton. The lattice is closed to a torus by periodic conditions for avoiding boundary effects. The hexagonal lattice was used, because it most naturally corresponds to the principle of densest packing of round projections of microhabitats. Each cell models a microhabitat which in a free state contains resources for existence of any one individual. A life of an individual lasts a one iteration of the automaton. All states of microhabitats have the same duration. All microhabitats are identical i.e. every individual of both species consumes identical quantity of identical resources.

Auto waves in active media according to,² a plant ecosystem may be considered ‘as a working mechanism’ which ‘maintains and regenerates itself.’ Our model demonstrates a such mechanism. From a more general physical point of view we model an active (excitable) media with auto waves (travelling waves, self-sustaining waves).^3-5 Active medium is a medium that contains distributed resources for maintenance of auto wave propagation. An auto wave is a self-organizing and self-sustaining dissipative structure. An active medium may be capable to regenerate its properties after local dissipation of resources. In our model, propagation of individuals occurs in the form of population waves. We use the axiomatic formalism of Wiener & Rosenblueth⁶ for modelling of excitation propagation in active media. In accordance with this formalism rest, excitation and refractoriness are the three successive states. In our formalism the rest state corresponds to the free state of a microhabitat, the excitation state corresponds to the life activity of an individual in a microhabitat and the refractory state corresponds to the regeneration state of a microhabitat. All states have identical duration. If the refractory period will be much longer than the active period, then such a model may be interpreted, for example, as propagation of the single wave of dry grass fire. Time duration of the basic states can be easily varied using additional states of the lattice sites.

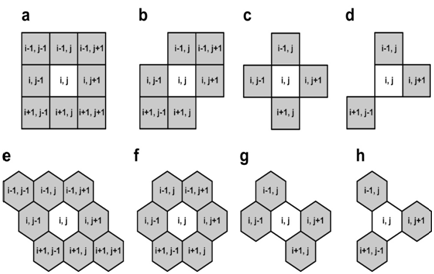
Figure 2 Various types of neighbourhoods of the cellular automaton.
Figures A-D Neighbourhoods on the square lattice - Moore, hexagonal, von Neumann and tripod.
Figures E-H The same neighbourhoods, but on the hexagonal lattice. On each iteration for each site with coordinates (i, j) of a lattice its neighbourhood is studied, taking into account periodic boundary conditions. The neighbourhoods on the hexagonal lattice are used for modelling fecundity rate of individuals.

Biological prototype of the model

A vegetative propagation of rhizomatous lawn grasses is the biological prototype of our model. Festuca rubra trichophylla (Slender creeping red fescue) is the prototype of aggressive vegetative propagation and Poa pratensis L. and Festuca rubra L. ssp. Rubra are the prototypes of moderate vegetative propagation. One individual corresponds to one tiller. A tiller is a minimal semi-autonomous grass shoot that sprouts from the base. Rhizomes are horizontal creeping underground shoots using which plants vegetatively (asexually) propagate. Unlike a root, rhizomes have buds and scaly leaves. One tiller may have maximum three or six rhizoms in the model. Three rhizoms per tiller correspond to moderate propagation (only a half of the nearest microhabitats) and six rhizoms per tiller correspond to aggressive vegetative propagation. A tiller with roots and leaves develops from a bud on the end of the rhizome. A populated microhabitat goes into the regeneration state after an individual’s death. The regeneration state of a site corresponds to the regeneration of microhabitat’s resources including recycling of a dead individual. All individuals are Glossary of terms identical. Propagation of off springs of one individual leads to colonization of the uniform, homogeneous and limited habitat.

Glossary of terms

The glossary of terms was used in design and interpretations of our models.
The terms: Active medium, smaves, Biological diversity, Cellular automaton, Dominance, Ecosystem, Fecundity, Fecundity rate, Fertility, Fertility rate, Field of the cellular automaton, Fitness, Habitat, Individual, A limiting factor of the environment, Macro habitat, Mechanistic mechanisms, Microhabitat, Mini habitat, Pacemaker, Phenomenological models and phenomenological mechanisms, Recessiveness, Rhizomes, Tiller, Uniform cellular automaton, White box model.

Active medium: A medium that contains distributed resources for maintenance of auto waves and capable to regenerate its properties after passage of auto wave in a result of pumping energy from outside. Ecosystem (habitat) is an example of an active medium, and life activity of species individuals is an example of an excited state of the environment.

Auto waves: self-sustaining waves of changes in states of the active medium, which are accompanied by energy dissipation. Auto wave’s properties are universal and independent of specific systems where they are implementing.

Biological diversity or biodiversity in the narrow sense (used here) means the number of different species, which are similar or identic trophic consumers living within the particular habitat.

Cellular automaton. Ecologically speaking, the cellular automaton is a spatio-temporal model of interrelations between each of all individual organisms, their microhabitats, minihabitats and the whole ecosystem. Integration of cells (microecosystems) into the whole ecosystem (macroecosystem) is carried out through defined neighbouring of each cell (miniecosystem). More formally speaking, cellular automaton is a polyautomaton (set of the identical finite automata), which consists of five objects <G, Z, N, f, P0>, where
G is a lattice of a cellular automaton consisting of an array of elements;
Z is a finite set of possible states of the elements of the lattice;
N is a cellular automata neighbourhood;
f is a function of transitions between states of a cell;
P0 is an initial cell-state pattern of the whole cellular-automaton field (a start states pattern).

A one iteration of the cellular automaton consists of applying the transition function to each element of the lattice. The iteration is completed only after the new state will be defined for all of its elements. A lattice of a cellular automaton consists of cells, which are identical finite automata and each of which may be in a predetermined number of discrete states. States of each of all cells are iteratively updating synchronously at discrete time steps according to local rules. A neighbourhood relation is defined over the lattice, indicating for each cell which cells are considered to be its neighbours. A neighbourhood consists of a cell and its defined neighbours. All cells have neighbourhoods of the same shape and the same rules for updating. These transition rules logically connect a state of each cell and states of its neighbouring cells on the given iteration with the state of the cell on the next iteration. In generalcellular automaton can be considered as a function that iteratively transforms an initial cell-state pattern of the whole cellular-automaton (a start states pattern) field into subsequent configurations. Neighbourhoods that are used in the models of the given work are presented in Figure 2.

1. Dominance: is defined as the primary ability of an individual to occupy a free microhabitat in a direct conflict of interests with an individual of another species. Antonym: excessiveness.
2. Ecosystem: is the unity of all interacting organisms and of their habitats.
3. Fecundity: is the potential for reproduction -the potential ability to produce off springs of an individual or population. Fecundity rate is a potential per capita off springs’ number on a next iteration.
4. Fertility: is the actual production of off springs -the actual reproductive rate of an individual. Fertility rate is an actual per capita off springs’ number on a next iteration.
5. Field of the cellular automaton: is the ordered set of cells (“micro eco-systems”, finite-state machines) where each cell corresponds to certain site of a uniform, regular lattice.
6. Fitness: is ability of individual to maintain its health, well being and directly competes for resources of environment. It is expressed in domination and describes how successful an organism is at leaving offspring compared to its direct competitors.
7. Habitat: is the intrinsic environment (the specific natural home) where a part of a species is able to survive. Habitat is a more general and less concretised term than ‘microhabitat’, ‘mini habitat’ and ‘macro habitat’ are (see the corresponding definitions of the Glossary and Figure 3, concreting the notion ‘habitat’ in the cellular automata context).
8. Individual: is one organism of a species (an autonomous agent in the most general case).
9. A limiting factor of the environment: is the environmental factor that controls an ability of the species individuals to thrive and to reproduce itself. These ecological factors limit bio efficiency (bio productivity) of organisms of the species when these factors are scarce.
10. Macro habitat: is the total environment where individuals may inhabit and propagate actually and potentially. Here, in the cellular automaton model, macro habitat is the entire field of the cellular automata without individuals. Macro habitat contains a complete set of all cells assigned to the sires of the cellular automaton lattice (Figure 3C).
11. Macro eco-system: is the macro habitat with individuals living in it.
12. Mechanistic mechanisms: permit most clearly to understand a system under study and to predict its behaviour. We consider mechanistic mechanisms as consisting of two constituents Causes-effects relations and Part-whole relations. The causes should be sufficient to understand their effects and the parts should be sufficient to understand the whole. In our research the “whole” is an ecosystem with populations of competing species. The “parts” are: individuals, microhabitats and interactions between the individuals and their immediate environment (neighbourhoods). We believe that the “causes” being investigated here are extreme principles of physics and in particular the Lotka's principle of maximum energy flux and the second law of thermodynamics. The “effects” are results of the inter specific competition. A deterministic, individual-based logical cellular-automata method developed in this study is the most suitable tool for search of the mechanistic mechanisms of complex systems. It is the white-box modelling method based on physically interpreted ecological axioms. These cellular automaton works as a visualising inference automaton of mechanistic insight into studied phenomena. It provides reducing of complex holistic dynamics of interspecific competition to the level of simple logical axioms.
13. Microhabitat: is the intrinsic physical environment where a particular individual inhabits. A microhabitat is a totality of all environmental conditions which are necessary for individual’s life (e.g. of a grass unit) and place where regeneration of the resources is possible. Here, in the cellular automaton model, a microhabitat is each discrete cell of the cellular automata field which corresponds to a specific site of the lattice of the cellular automaton. A cell represents a place which can be occupied by an individual autonomous agent (e.g. by an individual of a species) and contains the necessary resources for its individual life (Figure 3A).
14. Micro ecosystem: is the microhabitat with individual living in it.
15. Mini habitat: is the intrinsic physical environment (the specific natural home) where a particular individual of a species is able to propagate in one generation. Here, in the cellular automaton models a mini habitat is a cell together with its neighbouring cells, but without individuals (Figure 3B).
16. Mini ecosystem: is the mini habitat with individuals living in it.
17. Pacemaker: leading centre, auto-oscillation area in excitable (active) medium -a source of local self-oscillations which generates diverging auto wave. Within the limits of auto wave interpretations each separate organism, capable to autonomous reproduction may be considered as a pacemaker of population auto wave.
18. Phenomenological models and phenomenological mechanisms: showing what happens with modelled object on a macro-level but does not show how it happens on a mini- and a micro-level. They describe some empirical observations, but have no foundations in mechanisms or first principles, making difficult a prediction, generating new knowledge and the creation of new technologies. Phenomenological models are "black-box" models what mean that they are not transparent for understanding of underlying mechanisms of simulated objects. Metaphorically speaking, the phenomenological model is analogous to a picture of the studied phenomenon, drawn with the help of mathematical apparatus. Earlier Tilman noted that models of population dynamics based on differential equations are phenomenological and therefore hinder mechanistic understanding of phenomena under study.⁷
19. Recessiveness: is defined as the secondary (inferior) ability of an individual to occupy a free microhabitat in a direct conflict of interests with another competing individual. Antonym: dominance.
20. Rhizomesare: horizontal creeping underground shoots by means of which certain plants vegetatively (asexually) propagate themselves. Unlike a root, rhizomes have buds, nodes, and scaly leaves. Rhizome develops tillers with roots and leaves at nodes along its length.
21. Tiller is a minimal relatively autonomic grass shoot that sprouts from the base of grass and which is able to propagate.
22. Uniform cellular automaton applies the same rules for each cell.
23. White box (“clear box”, “glass box”, “open box”) model has a “transparent walls”- all events at all levels of the simulated dynamic system and at all stages of its dynamics are directly visible (Figure 4). White box model directly shows mechanistic mechanisms of the studied phenomena. It allows to obtain a new physical understanding of the studied system and to predict its future development. In the literature on ecological modeling the white-box modeling is discussed as a future opportunity.⁸ Currently, this type of modeling is used and widely discussed only in engineering sciences.^9-13 We consider the cellular automata method developed in this study as the white box modeling (Figure 5).

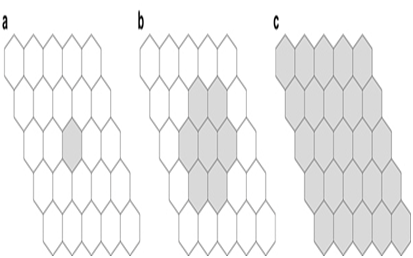
Figure 3 ‘Microhabitat’, ‘minihabitat’ and ‘macrohabitat’ on example of hexagonal neighbourhood on hexagonal lattice. The grey colour indicates:
 Figure 1A A microhabitat (any one cell of the field).
 Figure 1B A minihabitat (microhabitat and all the adjacent neighbouring cells).
 Figure 1C A macrohabitat (all field of the cellular automaton). The field consists of 5x5 cells and is used here as example.

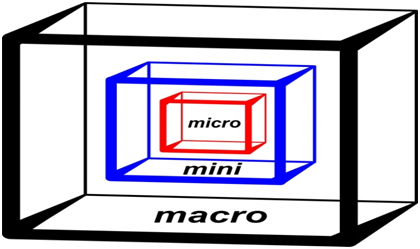
Figure 4 Figurative representation of white-box model.All events is visible on the macro-, mini- and micro-levels.

 Axioms of the cellular-automata model of ecosystem dynamics

Basic provisions of the models:

1. The lattice of the cellular automaton simulates аn ecosystem.
2. A single lattice site simulates a one micro ecosystem.
3. A neighbourhood simulates a mini ecosystem.
4. А one micro ecosystem may contain resources for life of a one individual of any species.
5. The used resources of a micro ecosystem are recovered after living circle of an individual during regeneration period

Types of states of a micro ecosystem:

1. Free (may be occupied);
2. Occupied by a one immobile individual of any species;
3. Regeneration - restoring conditions and resources of a micro ecosystem after an individuals's death and recycling of a dead individual of the first or the second species.

Properties of states of a micro ecosystem:

1. А free micro’rjsystem may be occupied only by one individual.
2. Populated micro ecosystem and micro ecosystem in the regeneration state cannot be occupied.
3. Occupied micro ecosystem goes into the regeneration state after an individual's death.
4. Micro ecosystem in the regeneration state becomes free or may be occupied immediately after finishing of the regeneration state (Figure 5).

Neighbourhood

1. A neighbourhood consists of a site and its intrinsically defined neighbour sites.
2. All sites have the same rules for updating.
3. А neighbourhood simulates an individual's mini ecosystem.
4. A neighbourhood also determines the number of possible off springs.

Cellular automata models of ecosystems

A single-species model

1. Characteristics of a single-species model.¹⁴
2. The hexagonal lattice is periodically closed to a torus.
3. The set of states of a lattice site is {0, 1, 2} for an ecosystem with a single species.
4. The graph of the transitions between the states of a site (Figure 6).
5. The cellular automata neighbourhoods (Figure 10).

Logical rules of transitions between the states of a microhabitat (Figure 6).
0→0, a microhabitat remains free if in its neighbourhood is no one living individual of a species.
0→1, a microhabitat is occupied by an individual if in its neighbourhood is at least one individual.
1→2, after an individual’s death a microhabitat goes into the regeneration state.
2→0, a microhabitat becomes free if in its neighbourhood is no one living individual.
2→1, a microhabitat is occupied by an individual, if in its neighbourhood is at least one individual.

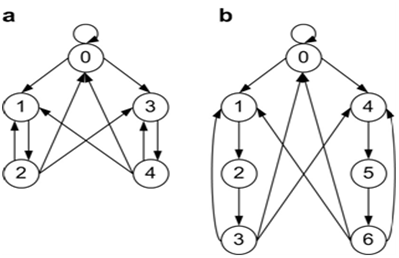
Figure 5 State transition graphs of the cellular automata models.
Figutre 5A Standard cellular automata:
0-a free microhabitat that can be occupied by an offspring of any species.
1–a microhabitat is occupied by a living individual of the first species.
2-a regeneration state of a microhabitat after living of an individual of the first species. In Supplementary
Movies this state is represented as symbol ‘.’
3 -a microhabitat is occupied by a living individual of the second species. In Supplementary Movies this state is represented as symbol ‘2’.
4 -a regeneration state of a microhabitat after living of an individual of the second species. In Supplementary Movies this state is represented as symbol ‘*’.

Figure 5B Cellular automata with additional ontogenic stages:
0–a free microhabitat that can be occupied by offsprings of any species.
1–a microhabitat is occupied by a living individual of the first species (1st ontogenic stage).
2–a microhabitat is occupied by a living individual of the first species (2nd ontogenic stage).
3–a regeneration state of a microhabitat after living of an individual of the first species.
4–a microhabitat is occupied by a living individual of the second species (1st ontogenic stage).
5–a microhabitat is occupied by a living individual of the second species (2nd ontogenic stage).
6–a regeneration state of a microhabitat after living of an individual of the second species.

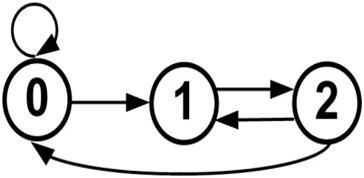
Figure 6 Graph of transitions between the states of a microhabitat in the single-species model.¹⁴
0 – a free microhabitat that can be occupied by an offspring of an individual;
1 – a microhabitat is occupied by a living individual;
2 – the regeneration state of a microhabitat after an individual’s death.

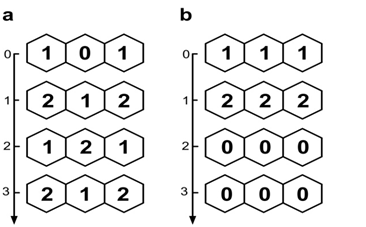
Figure 7 Examples of transformations of start states patterns in a model with one species. The one-dimensional lattice of three cells closed by periodic boundary conditions. Hexagonal neighbourhood is used for propagation.
Figure 7A Intraspecific competition between individuals of the same species.
Figure 7B The species disappears because there is no opportunity to reproduce.

A cellular automata model with these rules are presented in Figures 7 and 8. The lattice consists of 5x5 sites and the neighbourhood is hexagonal (Figure 8). The closest biological analogy of an individual’s propagation determined by a neighbourhood is asexual (vegetative) propagation of turf grasses by rhizomes. Population growth curve of this model is presented in Figure 9A The curve's smoothness depends on the lattice size (Figure 9B). This curve looks like a logistic one.

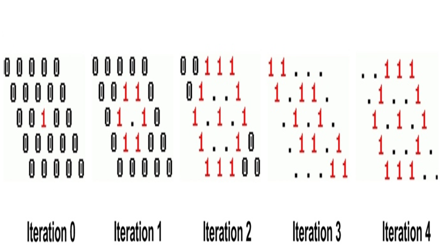
Figure 8 Colonization of the ecosystem by one species.¹⁴ ‘0’ – a free site of a microhabitat; ‘1’ – a microhabitat occupied by a living individual; ‘.’ – the regeneration state of a microhabitat is denoted here by the dot.

Another result is about importance of the neighbourhood type (Figure 10). We show how population growth rate depends on the neighbourhood type (Figure 10). A mechanism of double logistic-like curve (Figure 10 and Figure 11B) consists in moderate propagation of individuals what leads to gaps formation in population waves of propagating individuals and increases the time to occupy them. Gaps arise in result of moderate propagation when an individual may use for propagation only a half of the nearest resources. Such moderate propagation is simulated by the tripod neighbourhood (Figure 12H). The appearance mechanism of double logistic-like curve is based on the presence of gaps in the propagating population waves. When the waves reach the boundary of the lattice the additional filling of the remaining empty sites is occurred because of periodic conditions.

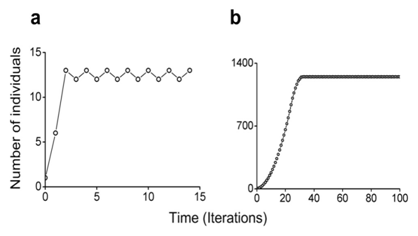
Figure 9 Single-species population dynamics.¹⁴ Logistic-like population growth curves. One individual is placed in ecosystem at the initial iteration.
Figure 9A The lattice consists of 5x5 sites.
Figure 9B The lattice consists of 50x50 sites.

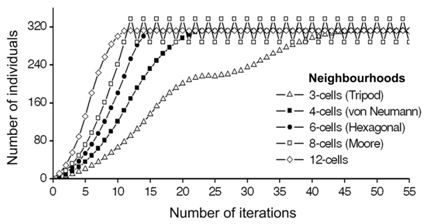
Figure 10 Relationship between a neighbourhood type and population growth rate. A possible number of offsprings per one individual is determined by the type of the cellular automata neighbourhood. Hexagonal lattice is of 25x25 sites. One individual is placed in ecosystem at the initial iteration.

A two-species competition model

1. Characteristics of the model:
2. The hexagonal lattice is closed to a torus.
3. The set of states of a lattice site is {0, 1, 2, 3, 4}.
4. The graph of the transitions between the states of a site (Figure 12).
5. Cellular automata neighbourhood is hexagonal (Figure 12F).

On the competitive exclusion principle

A niche is a habitat, which is an optimal combination of all environmental conditions and resources for growth, survival, and reproduction of the species. Here on an idealised two-species competition model, we consider a special case when a niche and a habitat are synonyms as a habitat is the combination of all environmental conditions and resources which are equally optimal for life activity of both competitors. Competitors are identical consumers with different fitness. We define fitness as the ability of an individual to survive and to propagate in a given environment and compete for its resources. The competition is carried out when various individuals are trying to use the same limiting resources (Figures 13A,C & Figure 14). An individual of the species with greater fitness is able to occupy a free microhabitat in a direct conflict of interest with an individual of the less adapted species (Figures 14A,B). The habitat is stable and the competing species have no any trade-offs. Increasing the ecosystem size by one microhabitat at the same cellular automaton rules leads to a stable coexistence of individuals of the competing species (Figure 13B & Figure 15). This is the simplest case of the strong violation of the competitive exclusion principle.¹⁵ A direct supplanting of one individual by another is impossible because we exclude predator-prey interactions between individuals in the model (Figure 15B). The violation of the competitive exclusion principle occurred due to the definite initial positioning of the individuals on the lattice, to regeneration processes in microhabitats, and to small size of the ecosystem (Figure 15). The small size of the ecosystem does not allow to individuals of the first species to bypass individuals of second species from “flanks”. The barrier of the two microhabitats in the regeneration state between individuals allows dividing the limiting resources peacefully (Figure 15C).

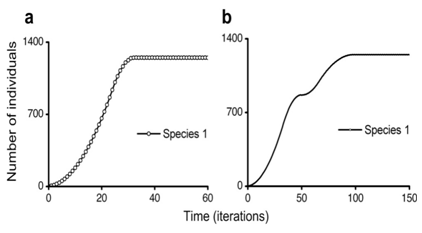
Figure 11 Population growth curves. The lattice consists of 50x50 sites.
Figure 11A Logistic-like curve.
Figure 11B Double logistic-like curve.

Thus, on the very simple cellular-automata model we have shown a mechanistic mechanism of how strong and weak competitors can stably coexist in one niche. Our model is deterministic individual based cellular automata and is a white-box model of inter specific competition. The particular relevance of the ecological modelling is linked to the global overexploitation of environment ("tragedy of the commons"), a significant increase in population, migrants, the problems of the peaceful coexistence of nations and peoples. The most intriguing mystery was the paradox of biodiversity. Historically, the biodiversity paradox arose as a contradiction between the competitive exclusion principle and the observed richness of tropically similar species.¹⁶ In theory, according to the competitive exclusion principle, complete competitors cannot coexist, but in practice, there are many examples of such coexistence: tropical rainforest, coral reefs, grasslands, plankton communities¹⁶ 1999). This contradiction has resulted in that “resolving the diversity paradox became the central issue in theoretical ecology”.¹⁷

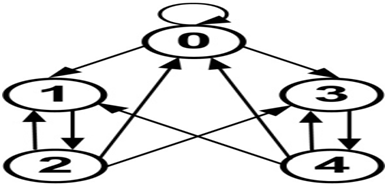
Figure 12 Graph of transitions between the states of a microhabitat in the two-species competition model .
0 – a free microhabitat that can be occupied by an offspring of any species;
1 – a microhabitat is occupied by a living individual of the first species;
2 – the regeneration state of a microhabitat after living of an individual of the first species;
3 – a microhabitat is occupied by a living individual of the second species;
4 – the regeneration state of a microhabitat after living of an individual of the second species.

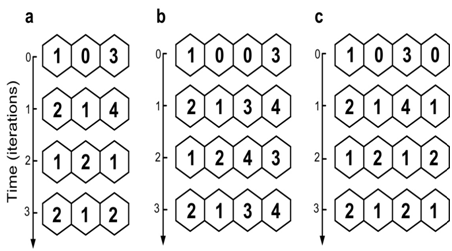
Figure 13 Examples of transformations of start states patterns in a model ecosystem with two competitors. The one-dimensional lattice of three cells closed by periodic boundary conditions. Hexagonal neighbourhood is used for propagation.
Figure 13A The species 1 displaces the less adapted species 2.
Figure 13B A violation of the competitive exclusion principle. Stable coexistence of two competitors in spite of their differences in fitness.
Figure 13C The species 1 displaces the less adapted species 2.

We have offered a logical solution to the biodiversity paradox. In order to solve this issue we verified the competitive exclusion principle by logical deterministic individual-based cellular automata.^3,15 These models are based on an ecological formalism of excitable medium. They are multi-level and completely mechanistic. We have verified most known formulations of the competitive exclusion principle and shown that identical consumers (complete competitors) which differ only in fitness can indefinitely coexist in one homogeneous habitat on one and the same limiting resource under constant conditions of the environment without any trade-offs and co-operations. The principle has been falsified. There are two possibilities- the principle is false and it should be rejected, or its definition is false and should be corrected. We have reformulated the competitive exclusion principle as follows:³ If each and every individual of a less fit species in any attempt to use any limiting resource always has a direct conflict of interest with an individual of a most fittest species and always loses, then, all other things being equal for all individuals of the competing species, these species cannot coexist indefinitely and the less fit species will be excluded from the habitat in the long run. This is a mechanistic definition of the principle. Its implementation in nature requires too strict conditions. The complexity and the extremely low probability of realization in nature of such stringent conditions eliminate the contradictions between the principle and the observed species richness. Thus the biodiversity paradox has been solved.¹⁸ Axiomatic cellular automata modelling is the promising way to a general theory of ecological physics.

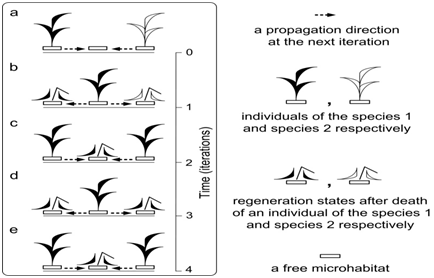
Figure 14 A case of the competitive exclusion of one species by another.¹⁵ The species 1 has greater fitness than the species 2.
Figure 14A The conflict of interest between individuals of competing species for a microhabitat for propagation.
Figure 14B The more adopted species wins in result of competition. Dead individuals are recycled at the regeneration state of a microhabitat.
Figure 14C-E The first species continues to live and propagate.

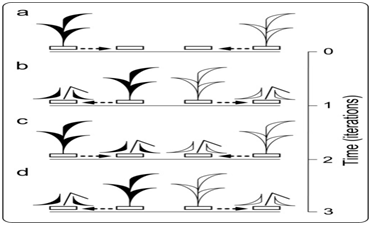
Figure 15 A violation of the competitive exclusion principle.¹⁵ Stable coexistence of two competitors in spite of their differences in fitness.
Figure 15A Individuals propagate in the adjacent free microhabitats. Direct conflicts of interest are absent.
Figure 15B  Individuals can not directly supplant each other because they are not a predator and a prey.
Figure 15C-D A stable cycle of coexistence of two species.

The proposed cellular automata models allow a mechanistic understanding of population and ecosystem dynamics. We consider the prospect of further development of the cellular automata approach as very challenging because it allows an individual-based modelling of complex spatio-temporal systems dynamics and permits unlimited extension by use of additional nested and adjoint lattices, additional states of sites, various types of neighbourhoods and individuals' behaviour rules with combination of the approach with the known modelling methods. In this regard, we want to express our opinion that further development of the theory of complex dynamic systems will be based on structures consisting of states of their subsystems and on transition diagram between these states. For nearly seventy years there is the appropriate language- the category theory.^19,20 Cellular automata are the appropriate instrument for categorical modelling of complex systems dynamics.

This research was partially supported by the Russian Foundation for Basic Research (grant no 16–31–00516).

The author declares there is no conflict of interest.

1. Tansley AG. The Use and Abuse of Vegetational Concepts and Terms. Ecology. 1935; 16 (3):284–307.              
2. Watt AS. Pattern and Process in the Plant Community. Journal of Ecology .1947;35(1–2):1–22.
3. Kalmykov LV, Kalmykov VL. Verification and reformulation of the competitive exclusion principle. Chaos, Solitons & Fractals. 2013;56:124–131.
4. Krinsky VI. Self–Organization: Auto waves and Structures Far from Equilibrium. Berlin Springer–Verlag. 1984:9–19.
5. Zaikin AN, Zhabotinsky AM. Concentration Wave Propagation in Two–dimensional Liquid–phase Self–oscillating System. Nature.1970; 225:535–537.
6. Wiener N, Rosenblueth A. The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Arch Inst Cardiol Mex. 1946;16(3):205–265.
7. Tilman D. The importance of the mechanisms of interspecific competition. Am Nat.1987;129(5):769–774.
8. Jørgensen SE, Bendoricchio G. Fundamentals of ecological modelling. 3rd ed. Amsterdam. New York Elsevier. 2001;530.
9. Kroll A. Grey–box models: Concepts and application. In: New Frontiers in Computational Intelligence and its Applications, of Frontiers in artificial intelligence and applications. Amsterdam: IOS Press. 2000(57).
10. Jelali M, Kroll A. Hydraulic servo–systems: modeling, identification, and control. London; New York: Springer. 2003:355.
11. Roffel B, Betlem BH. Advanced practical process control. Berlin. 2004:309.
12. Estrada–Flores S, Merts I, De Ketelaere B, et al. Development and validation of “grey–box” models for refrigeration applications: A review of key concepts. International Journal of Refrigeration. 2006;29(6):931–946.
13. Engel A. Verification, validation, and testing of engineered systems. Hoboken NJ Wiley, 2010;687.
14. Kalmykov LV, Kalmykov VL. A white–box model of S–shaped and double S–shaped single–species population growth. Peer J . 2015;3:e948.
15. Kalmykov LV, Kalmykov VL. A Solution to the Biodiversity Paradox by Logical Deterministic Cellular Automata. Acta Biotheoretica. 2015;63(2):203–221.
16. Sommer U. Ecology–Competition and coexistence. Nature. 1999;402(6760):366–367.
17. Lehman CL, Tilman D. Spatial ecology: the role of space in population. In: Tilman D, Kareiva PM, editors. Dynamics and interspecific interactions. Monographs in Population Biology Princeton University Press, Princeton, NJ: Princeton University Press. 1997;185–203.
18. Kalmykov VL, Kalmykov LV. On ecological modelling problems in the context of resolving the biodiversity paradox. Ecological Modelling. 2016;329:1–4.
19. Levich AP, Solov'Yov AV. Category–Functor Modelling of Natural Systems. Cybernetics and Systems.1999;30(6):571–585.
20. Goguen J. A categorical manifesto. Mathematical Structures in Computer Science.1991;49–67.