Computer programs applied to disaster simulation are widely used and widespread today, taking as input various data types, from specific to the application area to DTMs (Digital Terrain Models). This need for data input and, in particular, data related to relief is very relevant in prediction procedures for forecasting catastrophes, such as the failure of tailings mining deposit dams. Therefore, it is of fundamental importance to know and quantify the quality of this input data in question, in order to effectively serve this application. To this end, in this research, several tests were carried out, using as a reference for best results those obtained with the introduction of DTM from a LIDAR (Light Detection and Ranging) flight survey, this data being used as one of the primary and input into HEC-RAS (Hydrologic Engineering Center-River Analysis System). Subsequently, these same data had their spatial resolution degraded, that is, the pixel size increased, generating models with worse quality for new inputs and obtaining new simulation results of mining dam failures. The test area of the B1 Dam, located in Brumadinho-MG, Brazil, was used as a laboratory, where one of the biggest mining disasters in the world recently occurred and, for which, there are real data from the area affected by the dam collapse. The results obtained demonstrated that the use of an DTM with a spatial resolution of at least 2.5 meters or better, with DTM class A cartographic quality compatible with the most recent Brazilian standard, would guarantee reliable results.

Keywords: dam, digital terrain model, quality, mining, map accuracy standards, rupture

DTM, digital terrain model; HEC-RAS, hydrologic engineering center-river analysis system; LIDAR, light detection and ranging; MAS, map accuracy standards

The process of simulation and prediction of mineral exploration dam failure is extensively covered by several authors, and even similar themes using HEC-RAS (Hydrologic Engineering Center - River Analysis System) are presented in several references around the world.^1–12

In the context of the application of this technology and the present work, it is worth highlighting that the input of primary data, that is, topographic and/or cartographic data, is extremely important, in order to collaborate in this process, as stated and the aforementioned subject covered.^11–15 Thus, with the DTM (digital terrain model) as one of the main elements, considered this as a primary data of Cartography, this research sought to carry out several simulations and tests, in order to assess which spatial resolution would be sufficient. In this sense, we sought to ensure the presentation of dam rupture scenarios, which were as close as possible to reality and, in order to guarantee the safety of the population living in the surrounding area and the effects of the rupture on the environment of the affected region. . Considering these aspects, quality control of the DTM for each simulation scenario was carried out by adapting the Brazilian standard, as discussed in detail,^13–16 which is based on the control method positional quality of digital maps.¹⁷

It is also worth highlighting, in terms of the state of the art of quality control specific to DTMs, several reference works, such as the work carried out,¹⁸ where the authors analyze the topic over the last three decades;¹⁹ which addresses the perspectives and estimates of needs in terms of quality of DTMs through a study with users;²⁰ where comparison criteria are sought for the various global DTMs, taking into account the needs of users;²¹ a study where the authors, based on aspects of quality control of classes derived from the DTM, analyze the quality of the slope;²² where the authors study the state of the art of DTM generation using a deep learning process and also analyzing the final quality of the generated DTM;²³ where the authors used quasi-spline interpolation based on the Bernstein–Bézier coefficient to generate DTM and evaluated the final accuracy;²⁴ apply the buffer method to verify the elevation accuracy of the DTM;²⁵ evaluate the results generated by orbital DTMs for flood analysis and evaluate the coherence of the simulation performed.

In this article, an inference of quality control focused on altimetric data was carried out, considering the application of predictions of rupture of ore tailings dams from open mines. To this end, below, a brief theory will be presented on quality control in terms of altimetry applied to DTMs, the practical development with the definition of the study area and the details of each of the stages, the analysis of the results obtained and finally the final considerations.

Altimetric quality control theory applied to DTM

As in conventional cartography, where displacement is analyzed in the plane coordinates, precision, which is presented based on research carried out.^13–17 Once the control points via sampling have been established, they must be interpolated with the input and reference DTMs. Then, the altimetric difference between the input DTMs and the reference DTM are calculated, according to equation (1).

$\Delta Z_i=Z_i-Z_{ci}$   (1)

Where: ∆𝑍_𝑖= elevation error at point i of the sampling set of𝑛samples; 𝑍_𝑖= Altimetry of point i in the DTM under analysis; 𝑍_𝑐𝑖= Altimetry of point i in the reference DTM (greater accuracy).

It is expected that the errors found in the sample set are random and have a normal distribution, so that it is not possible to determine the reason for such a difference. The probability of an error greater than three times the standard deviation is small, although possible. Therefore, if these values ​​occur, the points must be inspected and, if an inconsistency is confirmed, excluded from the analyzes as they are considered gross errors.^15–17

To complete the analysis, the samples are subjected to two statistical tests, namely: the Normal Z test, which highlights the occurrence of systematic errors, and the Chi-square test (X²), which presents the precision of the sample set in relation to Brazilian regulations.¹⁷

The Z Trend Test is applied to a sample set with a large number of elements and reveals whether there are systematic errors in the set. Through equation (2).

$Z_H=\frac{1}{EP}*\mu *\sqrt{n}$   (2)

Where: Z_𝐻= the calculated Z value; 𝐸𝑃= S = σ= sample standard deviation; 𝜇= mean of the sample set; 𝑛= number of samples

From the statistical table we obtain 𝑍_(1−𝛼/2) based on the sample size and the significance α adopted in the analysis, a theoretical Z value is provided which, compared to the Z𝐻 value, indicates the occurrence or not of systematic errors in the samples. In the present study, a significance level of 0.1 was adopted.

This way we have the theoretical Z, according to equation 3.

$Z_{(1-\alpha /2)}=Z_{0.95}=1.6449$   (3)

Therefore, while the calculated Z value, Z_H, is greater than the theoretical Z,𝑍_0.95, there will be a systematic error in the altimetric component of the DTMs.

The Chi-square precision test is performed using equation (4) and reveals whether the analyzed data meets the quality standards established by the standard being applied. Therefore, the value of $X_{H,n-1}^2$ of the sampling point is compared to a calculated value𝑋𝑛2−1, which depends on the sample set n and the level of trust.

$X_{H,n-1}^2=(n-1)*S_H^2/{\sigma }_H^2$   (4)

Where: $X_{H,n-1}^2$ = X² calculated for the sample;𝑛= number of samples; $S_H^2$ = the square of the sample standard deviation; ${\sigma }_H^2$ = the square of the standard error of the precision class used.

The calculated value $X_{n-1,\alpha }^2$ ,  is obtained by equation (5) due to the number of samples.

$X_{n-1,\alpha }^2=df*{(1-p+z*\sqrt{p})}^3$   (5)

Where: df=n-1 = degrees of freedom; $p=\frac{2}{9}*df$ auxiliary variable; 𝑧 = −1.645 = value of the normal curve with area of ​​α = 0.1, on the right.

So, if $X_{H,n-1}^2$ ≤$X_{n-1,\alpha }^2$ , then the sample meets the tested accuracy. The concepts used can be better studied.^15–31

The quality parameter adopted was the Cartographic Accuracy Standard for Digital Cartographic Products CAS-DCP (PEC-PCD), which establishes 4 classes for framing geospatial data, considering the scale of the data. To do so, it is necessary that 90% of the sample values present an error below the value stipulated in the CAS-DCP (PEC-PCD) and that the altimetric variation between data under analysis and reference data present values less than or equal to the Maximum Error –ME and the Standard Error –SE(EP).^32–34 Considering the global context of experiences and applications of positional quality control standards in Cartography, it is worth consulting several additional sources in other countries, such as South Africa,^35–38 Australia,³⁹ Spain,⁴⁰ United States,^41–43 Mexico,^44,45 Portugal,⁴⁶ as well as that organized by bodies that bring together several countries, such as the NATO standard (Organization of North Atlantic Treaty⁴⁷).

As presented in ET-CQDG, the absolute positional accuracy for DTM, DEM and DSM data is obtained from the Maximum Error (ME) and the Standard Error SE (EP). These values applied in Table 1 establish the Cartographic Accuracy Standard for Digital Cartographic Products, CAS-DCP (PEC-PCD),^32–34 according to the reference class and scale.

The development of this job followed structured steps, based on the practical methodology based,^27–31 which was adapted for the purposes of this work. Thus, the general methodology research was structured according to Figure 1.

Figure 1 General research development methodology. Source: Authors (2024).

Study area

The study area (Figure 2) corresponds to the valley from the headwaters of Ribeirão Ferro-Carvão to its confluence with the Paraopeba River and, from then on, following this watercourse to the stretch where the river crosses the Serra do Funil, on the edge of the municipalities of Brumadinho, Mário Campos and São Joaquim de Bicas, State of Minas Gerais. This state corresponds to one of the largest in terms of territorial extension in Brazil, being the third economy in the GDP ranking, where the most important commercial activity corresponds to the mining sector.

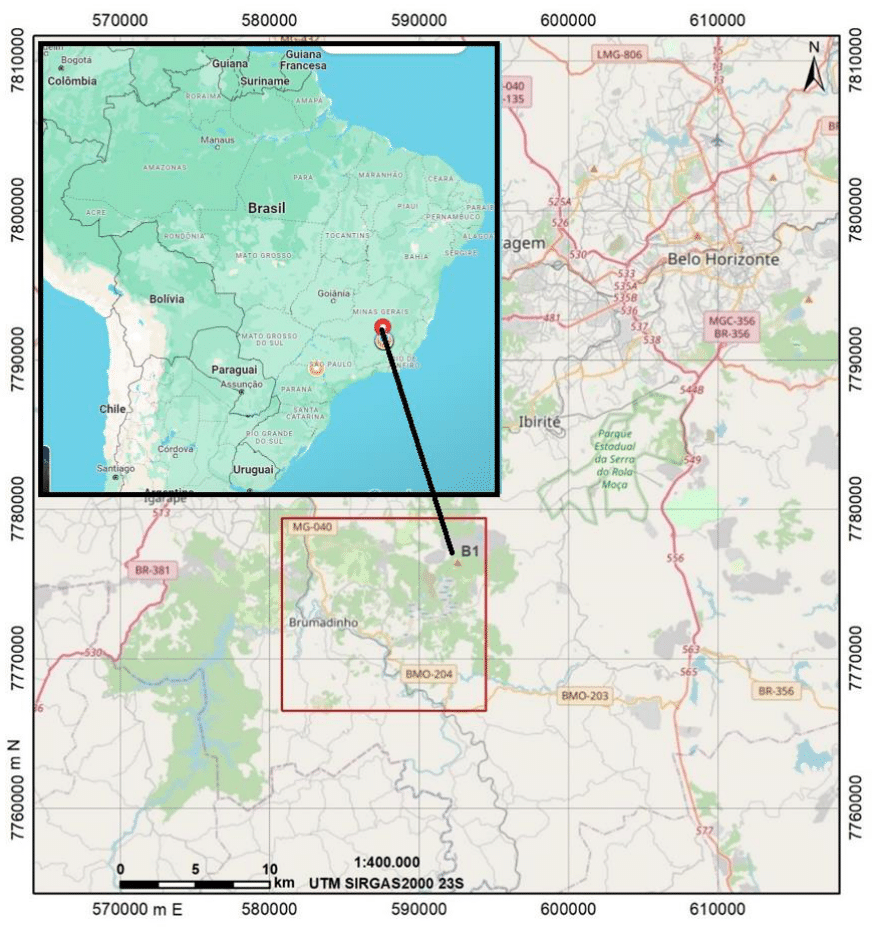
Figure 2 General location of the study area in relation to the city of Belo Horizonte – MG and Brazil.

In the most upstream portion of the valley is located the Córrego do Feijão Mine, operated by the mining company Vale, one of the largest in the world and leader in the sector in Brazil. Among the component structures, it is worth highlighting the B1 and B6 dams with storage capacity of 11.7x106 m³ and 4x106 m³ respectively, located at the head of Ribeirão Ferro-Carvão. Immediately below these structures, there is the ITM – Ore Treatment Installation followed by the railway stop, wagon loading yard for transporting the ore. Continuing with the description of the area, it is worth highlighting the buildings that made up the administrative part of the mine and, further down, two smaller dams B4 and B4A, for containing sediments (tailings).

Following, the course of Ribeirão Ferro-Carvão passes through the district of Córrego do Feijão, by Pousada Rural Nova Estância, followed by a railway bridge. At the end of the river there is the Parque da Cachoeira neighborhood where the Alberto Flores bridge stands out, close to the confluence with the Paraopeba River. In the section considered, the Paraopeba River is bordered by the urban center of the municipality of Brumadinho where there is a bridge on the MG040 highway. In the final stretch of the study area, the river crosses the Serra do Funil.

It is worth highlighting as a historical report that on January 25, 2019, the B1 tailings dam collapsed, after its mass underwent the liquefaction process, releasing the volume of iron ore tailings mud contained in its reservoir into the valley. downstream, described previously.⁴⁸ The dam failure mode occurred due to liquefaction of the massif, the breach formation time was 6 seconds and the reservoir volume propagation time was around 5 minutes.⁴⁸

During its propagation, the wave reached a speed of more than 90 km/h and a depth of more than 40 meters.^48,49 As a consequence, most of the operational area of ​​the Córrego do Feijão Mine was destroyed, as were the structures and houses along the Ribeirão Ferro-Carvão valley, resulting in 259 people dead and 11 missing.⁵⁰

The wave reached the administrative part of the mine in less than 2 minutes. Due to the geomorphological characteristics of the valley downstream and with the incorporation of material along the wave path, the speed decreased considerably, taking around 30 minutes to reach the region of the Nova Estância guesthouse. Finally, at around 3:50 pm the wave reached the Paraopeba River, after more than 3 hours of the collapse of Dam 1.⁴⁹

Figure 3 presents a greater detail of the study area with the main elements observed, and Figure 4 presents an example of the visual appearance of part of the study area before and after the dam collapse.

Figure 3 Detail of the study area.
Source: 13.

Figure 4 Detail of part of the affected area before and after the rupture.
Source: 13.

In the data selection and processing procedures in the Geographic Information System – GIS, the ArcGIS and QGIS programs were used,^51–53 including the tools and applications associated with them.

DTM degradation

Furthermore, it is worth highlighting and presenting details of the DTM images, which were generated from the original file to those degraded with the worsening of spatial resolution to carry out practical tests for introduction into HEC-RAS, generating different simulation scenarios. This can be seen in Figure 5, where there is the original image from DTM (C01, 1 meter pixel spatial resolution) to the others (C05, 5 meters; C10, 10 meters; C15, 15 meters; C20, 20 meters; C25, 25 meters), with bilinear interpolation being applied in this process in a GIS program.^51–53 In these figures, you can see the difference in visualization of the railway line layout.

Figure 5 Detail of part of the affected area before and after the rupture.
Source: 13.

Sample size, distribution and selection

When locating the sampling points, locations were considered that did not undergo changes due to the rupture of Dam B1 and that were less likely to change their morphological characteristics over time. In this way, preference was given to demarcating control points in easement areas, access roads and railways, identified in the orthophotos used in this study.

In total, 247 points were established to control the vertical accuracy of the DTMs, selected as shown in Figure 6. These sample points were interpolated to obtain the altimetric value in each input DTM, previously presented in Figure 5, and in the reference DTM, coming from of the LIDAR survey.

Figure 6 Sample of control points in the study area.
Source: 13.

Statistics analysis

The synthesis of the descriptive statistics of the data, the trend and precision tests and the quality standard of the evaluated DTMs (C01, 1 meter, C05, 5 meters; C10, 10 meters; C15, 15 meters; C20, 20 meters; C25, 25 meters) based on the previously presented theory are presented in Table 2. In this same Table 2, all the classical statistics developed are presented, considering the corresponding sample of each of the DTMs with different spatial resolutions/pixel size (C01 , 1 meter, DTM_1m; C05, 5 meters, DTM_5m; C10, 10 meters, DTM_10m; C15, 15 meters, DTM_15m; C20, 20 meters, DTM_20m; C25, 25 meters, DTM_25m). In addition, several other variables are presented in this same table, namely: mean, median, mode, standard error, standard deviation, sample variance, kurtosis, mean plus 3 standard deviations, mean minus 3 standard deviations, asymmetry, interval, minimum, maximum, sum and sample size.

Taking a more visual approach, Figure 7 shows the error distribution graphs for each of the DTMs that were used in the dam failure simulations in HEC-RAS processing. It can be seen that, as expected, the data does not adhere to a normal distribution. However, this is an increasingly common pattern in the engineering area and more specifically in terms of geotechnologies, considering data collection with DRONES and GNSS, in terms of positional accuracy, obtaining the closest and most adherent results. the reality.

Figure 7 Distribution of sample errors from each simulation.
Source: 13.

Next, considering the cartographic quality inferences, the concepts of the item referring to the Theory of altimetric quality control applied to the DTM, already presented previously, were applied. Thus, the results in terms of cartographic quality are presented in Table 3, as well as the final classification according to the standards of the Brazilian standard (see based on the parameters in Table 2,^32–34).

Dum break inferences

Before even starting the dissertation on this item, it is worth highlighting that the main objective of this article was to report the application and proposition of an innovative methodology for quality control of DTMs used in the dam failure simulation process and their influence, in particular with respect to HEC-RAS.^54–56 In terms of theory and concepts of the parameters and variables that will be reported and evaluated here, there is already a vast list of documentation and scientific articles, with emphasis on,^1–14 which are used in hydrology and widely discussed and enshrined in the language of this scientific area. Therefore, there was no need to address these issues in theoretical terms, moving more towards application.

In the process of evaluating the results of dam failure parameters, the objective was to analyze the impacts in terms of the classification of each DTM of different spatial resolutions (pixel size) on the simulation results. To this end, the analysis of the flooded area forecast (performance indicator F) was verified, as well as the values ​​obtained for depth, speed and arrival time of the waste wave. Where the columns with C01, C05, C10, C20 and C25, respectively correspond to the scenarios associated with the DTMs of the different spatial resolutions of 1 m, 5 m, 10 m, 20 m and 25 m, respectively.

The performance indicator F was obtained by comparing the flooded area mapped in the post-rupture orthophoto and the flooded areas calculated in the simulated scenarios. Thus, the results shown in Table 4.¹³ and plotted in the graphs in Figure 8,¹³ considering the Bias values ​​all above 1.0, demonstrate that the scenarios tended to overestimate the flood level; as shown by the penalty rates for overestimates, F4, with values ​​around 0.6; The F² index above 0.8 indicates the critical success achieved by all scenarios in predicting flood spots.

Figure 8 Performance indicator graphs F.
Source: 13.

In terms of classification of affected areas (A-coherent; B-overestimated; C-underestimated), compared to reality, Table 5 is presented.

Analyzing Table 6, we have to:

1. 1) the total of areas coherent with the reality of the disaster that occurred (A-coherent, marked in brown), with the highest value found in C05 being 264.56 ha (very close to C01, 264.49 ha) and the least coherent being the area of scenario C25 of 260.78 ha;
2. in terms of overestimated area (B-overestimated, marked in blue) we have in C05 the value of 52.55 ha (being the most alarming and very close to C01 of 51.52 ha), with the least alarming being C25, pointing to the area of ​​45.12 ha (see blue marking, with a difference of 7.43 ha);
3. considering the underestimated areas (C-underestimated, marked in red) there would be the highest value and, therefore, the greatest error in decision-making, which could lead to negligence and the occurrence of fatalities, would be the C25 with 9.04 ha; C05, with a value of 5.73 ha (very close to C01 of 5.86 ha), being presented as the most coherent and, therefore, the lowest risk in decision making), indicating a difference of 3.18 ha, that is, of 63.38% increased risk of making mistakes when making a decision;
4. in terms of what would be real (marked in black) and, considering the spatial resolution, C01 would be the closest to the real area due to the fact that it has the best spatial resolution, having the total area considering A, B and C, of ​​321.87 ha and although C05 had a very close value (322.83 ha, difference of just 0.3%, that is, practically equal); when comparing with the theoretically less precise scenario (C25), due to its worse spatial resolution, with an area of ​​314.95 ha, there is a difference of 6.92 ha), which would represent a difference of 2.14%, the which depending on the area could be considerable.

On the other hand, in visual terms in the representation, in the form of maps of these same scenarios and, considering the scale of representation, as seen in Figure 9, the values ​​presented are very close, being practically imperceptible.

Figure 9 Performance indicator graphs F.
Source: 13.

Continuing the application's inferences, it is clear that the fluid simulated in the scenarios did not travel the entire length of the calculation mesh, reaching the stability condition just after the representative section ST-10 (fluid transport section-10, of the total out of 14 that were considered). The results of depth, speed and wave arrival time in the sections are represented in Tables 6–8, analytically and visually in the graphs in Figures 10–12.

In terms of maximum depth, see Table 6 and Figure 10.

Observing Table 6 and the graph in Figure 10, it can be seen that in relation to maximum depths, the greatest variation occurred in the initial cross section, ST-01, and in the final ones, from ST-07, already in the middle end of the wave propagation section. When observing Table 7 and the graph in Figure 11, in relation to the speeds in the final sections, ST-09 and ST-10, there is greater sensitivity to variation in the terrain scale. Regarding arrival times, which can be seen in Table 8 and the graph in Figure 12, it can be seen that in the first stretches, more specifically in the first 3 kilometers, there was no great variation, with a significant difference being found from the section ST-06. Finally, analyzing the set, maximum speed was the metric that showed the greatest variation between scenarios with an average of 4.2%, followed by maximum depth with 3.75% and finally, the arrival time of the wave with 2%.

Figure 10 Maximum depth graph.
Source: 13.

Figure 11 Maximum speed graph.
Source: 13.

Figure 12 Arrival time graph.
Source: 13.

In terms of compatible cartographic quality for the application of the research developed in this scientific and practical work in the field of Mining Engineering and Mineral Extraction, the DTMs tested reached the quality standards established in the CAS-DCP (PEC-PCD), compatible with scales from 1:2,000 to 1:10,000, with maximum errors varying between 0.75 and 2.5 meters, considering the statistical margin of gross error (three times the standard error).

Among the metrics analyzed, the maximum propagation speed of the waste flow in the sections was the variable that presented the greatest sensitivity with a variation of 4.21%, followed by the depth with 3.75% and finally, the arrival time of the wave. which presented a 2.07% variation.

Regarding the arrival time, when analyzing the results of the cross sections more specifically, it is clear that in the first initial section of three sections, up to section ST-05, no change in the simulation result was found in this item. corresponding to the arrival time. It was found that the most sensitive change occurred in the last section, in the Paraopeba River, where the arrival time showed a maximum difference of 1 minute and 50 seconds, in relation to the average time of the different scenarios presented. When compared with the real event, it can be said that the model failed to represent the real chronology of the event. One of the possible reasons for this is due to the fact that although HEC-RAS version 6.0 contemplates the propagation of viscous fluids, it still does not have the ability to vary the volumetric concentration of this fluid in time-space, as the wave it incorporates the disturbed material along its path.

The depth results showed an average standard deviation of 50 centimeters, with the greatest depth difference found in the ST-01 section, corresponding to 1.16 meters around the average. This difference occurred precisely in the C25 simulation scenario, where the terrain has worse spatial resolution.

Regarding the maximum speed results, it is notable that the large difference in values ​​occurred in the final section of the simulation, reaching a variation above 10%. When comparing the values ​​of the representative sections and the observed values, a certain coherence can be seen between what occurred and what was simulated.

The impacted area defined in each scenario was analyzed using the performance indicator F, which demonstrates that the results obtained are not biased and that they achieved critical success greater than 80% according to F². The overestimated areas were responsible for most of the errors, as demonstrated by indicators F3 and F4, which penalized the underestimated and overestimated flood areas, respectively, as also discussed and commented in the item called Dum break inferences. In a way, overestimated areas have a less harmful effect than an area impacted in a real rupture event and not predicted in a simulated event, since it is the simulated flood spots that will support the development of emergency action plans. evacuation and rescue.

In general, it is possible to state that the scenarios presented a very similar performance in explaining the rupture of Dam 1, and that speed was the most sensitive variable to the change in terrain, without, however, presenting a very discrepant response in relation to the other metrics. analyzed. Thus, scales more detailed than 1:10,000 are capable of representing an event of the magnitude of Dam B1.

However, the results demonstrate an even greater need to deepen the scale analysis of terrain representation for the simulation of dam rupture events. In this sense, similar research applied to other dams with different characteristics and different downstream valleys can help to elucidate a compatible minimum scale for the development of rupture studies.

The results can also serve as a basis for defining guidelines for mapping valleys downstream of dams, optimizing resources without losing in terms of information quality.

Finally, it is worth highlighting that the diagnosis and prediction of the disaster studied here can serve as a good practical methodological basis, providing support for the definition and classification of risk areas with these characteristics. All of this could be associated with a multivariate analysis, in order to classify the risk areas with the highest and lowest priority for evacuation. Additionally, the brigade team and the public authorities could carry out training, awareness and simulation of the evacuation of the area, training the population residing in these areas, in order to prepare them for a real situation and avoid fatalities. In another context, to be studied, new conduct and planning for the recovery of these waste areas could be adopted, such as the drainage of the dammed product, with the use of waste material (for example in the production of bricks) . It is also worth considering the recovery of the environment in the degraded area with the reforestation and restoration of the region's native forest, which is already adopted by some mining companies in Brazil.

Acknowledgments for the Analysis and Modeling from Environmental System Post Graduation Program of Federal University of Minas Gerais State - Brazil.

None.

There is no conflict of interest.

1. Peker İB, Gülbaz S, Demir V, et al. Integration of HEC-RAS and HEC-HMS with GIS in Flood Modeling and Flood Hazard Mapping. Sustainability. 2024;16(3):1226.
2. Doğan E, Temiz T, Sönmez O, et al. Dam failure analysis according to different methods in HEC-RAS, Gökçe Dam, Turkey. Acta Scientiarum Technology. 2024;46(1).
3. Tessema BH, Gebremedhn AY, Getahun YS. Dam breach analysis and flood inundation mapping of Dire Dam, using HEC-HMS and HEC-RAS models. Sustainable Water Resources Management. 2024;10(2):45.
4. Rahman M, Ali Md Shahjahan. Drivers of tidal flow variability in the Pussur fluvial estuary: A numerical study by HEC-RAS. Heliyon, 2024.
5. Ennouini W, Fenocchi A, Petaccia G, et al. A complete methodology to assess hydraulic risk in small ungauged catchments based on HEC-RAS 2D Rain-On-Grid simulations. Natural Hazards. 2024:1–29.
6. Kannapiran UM, Bhaskar AS. Flood inundation mapping of upstream region in the Adyar River basin: Integrating hydrologic engineering center's river analysis system (HEC-RAS) approach with groundwater considerations. Groundwater for Sustainable Development. 2024;24:101085.
7. Nathanael E, Sejati W. Effective government management of flood discharge in drainage channels using HEC-RAS 6.3. 1 application. APTISI Transactions on Management. 2023;7(3):210–220.
8. Sathya A, Thampi SG, Chithra NR. Development of a framework for sand auditing of the Chaliyar River basin, Kerala, India using HEC-HMS and HEC-RAS model coupling. International Journal of River Basin Management. 2023;21(1):67–80.
9. Namara WG, Damisse TA, Tufa FG. Application of HEC-RAS and HEC-GeoRAS model for flood inundation mapping, the case of Awash bello flood plain, upper Awash River Basin, oromiya regional state, Ethiopia. Modeling Earth Systems and Environment. 2022;8(2):1449–1460.
10. Mendes TA, Sousa MBD, Pereira SADS, et al. Use of the HEC-RAS model based on LiDAR information to assess urban flooding. Sanitary and Environmental Engineering. 2022;27:141–157.
11. Morais VTP, Nero MA, Elmiro MAT, et al. Systematic review on the use of digital terrain models in dam rupture simulations. Int J Hydro. 2022;6(5):197–200.
12. Peixoto JS, de Moraes MAE, Garcia K, et al. Performance analysis of the lisflood hydrological model in a flood event in the Madeira river basin. Int J Hydro. 2024;8(2):38‒43.
13. Morais VTP de. Use of digital terrain models with different spatial resolutions from Lidar data in the simulation of the Dam rupture in Brumadinho-Minas Gerais. 2021.
14. Lima RP, Elmiro MAT, Nero MA, et al. Assessment of digital terrain models in dam break simulation studies. Bulletin of Geodetic Sciences. 2021;27:e2021005.
15. Ferreira FR. Proposal for evaluating the altimetric accuracy of LIDAR data (Doctoral dissertation). 2019.
16. Ferreira FR, Cintra JP. Assessment of the altimetric accuracy of Light Detection and Ranging (LIDAR) data. Multidisciplinary Scientific Journal Knowledge Center. 2021;10:14–41.
17. Cintra JP, Nero MA. New method for positional cartographic quality control in digital mapping. Journal of surveying engineering. 2015;141(3):04015001.
18. Mesa-Mingorance JL, Ariza-López FJ. Accuracy assessment of digital elevation models (DEMs): A critical review of practices of the past three decades. Remote Sensing. 2020;12(16):2630.
19. Ariza-López FJ, Mora EGC, Mingorance JLM, et al. DEMs: An approach to users and uses from the quality perspective. International Journal of Spatial Data Infrastructures Research. 2018;13:131–171.
20. López-Vázquez C, Ariza-López FJ. Global digital elevation model comparison criteria: an evident need to consider their application. ISPRS International Journal of Geo-Information. 2023;12(8):337.
21. Alba-Fernández MV, Ariza-López FJ, Jiménez-Gamero MD. A new approach to the quality control of slope and aspect classes derived from digital elevation models. Remote Sensing. 2021;13(11):2069.
22. Ruiz-Lendínez JJ, Ariza-López FJ, Reinoso-Gordo JF, et al. Deep learning methods applied to digital elevation models: state of the art. Geocarto International. 2023;38(1):2252389.
23. Ariza‐López FJ, Barrera D, Eddargani S, et al. Spline quasi‐interpolation in the Bernstein basis and its application to digital elevation models. Mathematical Methods in the Applied Sciences. 2023;46(2):1687–1698.
24. Ariza-López FJ, Reinoso-Gordo JF. Edge methods for evaluating elevation accuracy in digital terrain elevation models. Cartographic Magazine. 2021;(103):33–45.
25. Rau MI, Julzarika A, Yoshikawa N, et al. Application of topographic elevation data generated by remote sensing approaches to flood inundation analysis model. Paddy and Water Environment. 2024:1–15.
26. Nero MA, Cintra JP, Ferreira GDF, et al. A computational tool to evaluate the sample size in map positional accuracy. Bulletin of Geodetic Sciences. 2017;23:445–460.
27. Nero MA, Pereira TÁJ, de Paulo Ramos M. Positional quality control of orthoimages from satellite images with good spatial resolution according to PEC-PCD. Revista Contemporânea. 2022;2(6):1235–1251.
28. Nero MA. Proposals for quality control of cartographic bases with emphasis on the positional component (Doctoral dissertation, University of São Paulo). 2005.
29. Nogueira Júnior JB. Quality control of cartographic products: a methodological proposal (Doctoral dissertation, Universidade Estadual Paulista). 2003.
30. Santos ADPD. Cartographic quality control: methodologies for evaluating positional accuracy in spatial data. (Doctoral dissertation, Federal University of Viçosa). 2015.
31. Ariza-López FJ, García-Balboa J, Rodríguez-Avi J, et al. Guide for the positional accuracy assessment of geospatial data. Pan American Institute of Geography and History, Occasional Publication. 2021;563.
32. DSG-geographic service board. Technical specification for geospatial data quality control (ET-CQDG). 2016.
33. DSG-geographic service directorate. Technical specification standard for acquisition of vector geospatial data for the defense of the Land Force (ET-ADGV Defense F Ter), 2nd Edn. 2016.
34. BRAZIL. Decree No. 89,817 of June 20, 1984. Establishes the regulatory instructions for the technical standards of National Cartography. Brazil. 1984.
35. DRDLR. Department Rural Development and Land Reform. Standard for the 1:10 000 Orthophoto Map Series. Republic of South Africa. 2018.
36. DRDLR - Department Rural Development and Land Reform. Standard for the 1:50 000 Orthophoto Map Series. Republic of South Africa. 2023.
37. DRDLR - Department Rural Development and Land Reform. Standard for the 1:250 000 Orthophoto Map Series. Republic of South Africa. 2017.
38. DRDLR - Department Rural Development and Land Reform. Standard for the 1:500 000 Orthophoto Map Series. Republic of South Africa. 2017.
39. ICSM - Intergovernmental Committee on Survey and Mapping. Australian map and spatial horizontal data accuracy standard. Australia. 2009.
40. AENOR - Spanish Standardization and Certification Association. UNE 148002:2016: Methodology for evaluating the positional accuracy of geographic information. Madrid. 2016. 46 p.
41. Federal Geographic Data Committee. Geospatial positioning accuracy standards part 3: National standard for spatial data accuracy. US Geological Survey. 1998.
42. Abdullah Q. The ASPRS positional accuracy standards. Edition 2: The Geospatial Mapping Industry Guide to Best Practices. Photogrammetric Engineering & Remote Sensing. 2023;89(10):581–588.
43. ASPRS - American Society for Photogrammetry and Remote Sensing. ASPRS positional accuracy standards for digital geospatial data. Photogramm. Eng Remote Sens. 2015;81(3):A1–A26.
44. INEGI - National Institute of Statistics and Geography. Technical standard for positional accuracy standards. Official Gazette of the Federation on December 23, 2010. 2011.
45. INEGI - National Institute of Statistics and Geography. Spatial data calidation model: Technical annex 2 - evaluation of spatial data calibration. 2009.
46. ​​DGT - General Directorate of the Territory. Standards and technical specifications for vector and image topographic cartography. Portugal. 2020.
47. NSA - Nato Standardization Agency. Evaluation of land maps, aeronautical charts and digital topographic data. STANAG (Standardization Agreement) No. 2215. 7th Edn. (Text not published), NATO, Brussels. 2010.
48. Robertson PK, Melo L, Williams DJ, et al. Report of the expert panel on the technical causes of the failure of Feijão Dam I. Commissioned by Vale. 2019. 81 p.
49. Ragazzi L, Rocha M. Brumadinho: the engineering of a crime. Letramento Publisher. 2021.
50. CBMMG. Tragedy in Brumadinho completes two years and is marked by tributes to the victims. 2021.
51. ESRI. ArcGIS sesktop. Cut fill, 2021.
52. ESRI. ArcGIS desktop. Image classification using the ArcGIS Spatial Analyst extension, 2021.
53. QGIS. org, QGIS [software], Version 3.18.1, QGIS. org. 2020.
54. USACE- US Army Corps of Engineers. HEC-RAS river analysis system. 2D modeling user's manual. Version 6.0. Davis, CA: US Army Corps of Engineers. Institute for Water Resources, Hydrologic Engineering Center. 2023.
55. USACE - US Army Corps of Engineers. HEC-RAS river analysis system. 2D modeling user's manual. Version 6.0. Davis, CA: US Army Corps of Engineers. Institute for Water Resources, Hydrologic Engineering Center. 2024.
56. Brunner GW. HEC-RAS river analysis system 2D modeling user's manual version 6.4.1. US Army Corps of Engineers—Hydrologic Engineering Center. 2023:1–171.